Козлов В.В. Надёжность горных машин и оборудования

Подождите немного. Документ загружается.

191

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

1. Поломка и излом, виды изломов.

2. Износ, в чем проявляется, как измеряется?

3. Виды изнашиваемости деталей.

4. Какова физическая природа отказов горных машин?

5. Коррозия, на что она влияет? Виды коррозии.

6. Виды трения и методы борьбы с ними.

7. Что такое кинематическая вязкость, в чем она измеряет-

ся?

8. От чего зависит износостойкость деталей?

192

Глава 11

ИСПЫТАНИЯ НОВОЙ ТЕХНИКИ

11.1 Виды и планы испытания новой техники

Испытания на надежность являются необходимым этапом

последовательного процесса проектирования и изготовления но-

вого оборудования. Испытания проводятся с целью: обнаружить

и устранить непредвиденные отказы; получить числовые значе-

ния показателей надежности; определить соответствие готовых

изделий заданным требованиям по надежности; дать рекоменда-

ции по повышению надежности.

В соответствии с ГОСТ16504-70 виды испытаний класси-

фицируются по следующим признакам:

- по целям, куда относятся контрольные испытания (пред-

варительные, государственные, межведомственные, приемо-

сдаточ-ные, периодические, типовые) и исследовательские (атте-

стационные, граничные);

- по срокам проведения (ускоренные, неускоренные);

- по методу проведения (разрушающие, неразрушающие);

- по этапам (на этапе производства и эксплуатационные).

Особое место в общей оценке машин занимают испытания:

- на надежность опытных образцов (определительные);

- на надежность серийных образцов (контрольные);

- ресурсные;

Предварительные испытания опытных образцов или

опытных партий проводятся заводом-изготовителем для решения

вопроса о возможности представления изделия (продукции) на

государственные, межведомственные или ведомственные испы-

тания.

193

Контрольные испытания проводятся для контроля каче-

ства продукции, куда входят: предварительные, государственные,

межведомственные, приемно-сдаточные, периодические и типо-

вые.

Контрольные испытания на надежность проводят по плану

ГОСТ 27.410-87, который содержит сведения: [См. приложение

А]

- о количестве изделий, поставленных на испытание N

(объем выработки);

- о характере проведения испытаний {U, R, M};

- о длительности испытаний {T, T

∑

, S} и, наконец, инфор-

мация о количестве отказов или отказавших объектов {r}.

Суммарная наработка за период (o, t} определяется

[ ]

rNttT

−+=

∑

где t – реально текущее время;

r – число оказавших объектов за время t.

Среди различных планов особое место занимают три типа

испытаний:

1. с ограниченным числом отказов [NUR], [NRr], [Nmr].

В этой группе планов испытания прекращаются после наступле-

ния заранее назначенного числа отказов r;

2. ограниченной продолжительности [NUT], [NRT],

[NMT]. В этой группе планов испытания прекращаются по исте-

чении назначенного заранее времени Т;

3. последовательные планы. В этой группе планов заранее

не устанавливается ни число отказов, ни время испытаний. Реше-

194

ние о прекращении испытаний вырабатывается на основе резуль-

татов, полученных в ходе опыта. Например, на основе текущей

суммарной наработки. Последовательные планы чаще всех ис-

пользуются при испытаниях на надежность.

11.2 Определительные испытания

Во многих случаях испытания на надежность необходимо

проводить до разрушения. Поэтому испытывают не все изделия

(генеральную совокупность), а небольшую их часть, называемую

выборкой. В этом случае вероятность безотказной работы (на-

дежность) изделия, средняя наработка на отказ и среднее время

восстановления могут отличаться от соответствующих статисти-

ческих оценок вследствие ограниченности и случайного состава

выборки. Чтобы учесть это возможное отличие, вводится понятие

доверительной вероятности.

Доверительный интервал для вероятности Р ограни-

чен нижней Р

и верхней Р

доверительной границами:

Вер(Р

≤ Р ≤ Р

) = β, (11.1)

где символ “Вер” обозначает вероятность события, а β показыва-

ет значение двусторонней доверительной вероятности, т.е. веро-

ятность попадания в интервал, ограниченный с двух сторон. Ана-

Доверительной вероятностью (достоверностью) называют

вероятность того, что истинное значение оцениваемого

параметра или числовой характеристики лежит в задан-

ном интервале, называемом доверительным.

195

логично, доверительный интервал для средней наработки на отказ

ограничен Т

и Т

, а для среднего времени восстановления – гра-

ницами Т

вн

, Т

вв

На практике основной интерес представляет односторонняя

вероятность, что числовая характеристика не меньше нижней и не

выше верхней границы. Первое условие, в частности, относится

к вероятности безотказной работы и средней наработке на отказ,

второе – к среднему времени восстановления. Например, для

вероятности безотказной работы условие имеет вид

Вер (Р

≤ Р) = α. (11.2)

Здесь α - одностороняя доверительная вероятность нахож-

дения рассматриваемой числовой характеристики в интервале,

ограниченном с одной стороны. Вероятность α на стадии испыта-

ний опытных образцов принимают равной 0,7 ...0,8, на стадии

передачи разработки в серийное производство 0,9...0,95. Нижние

значения характерны для случая мелкосерийного производства и

высокой стоимости испытаний.

Ниже приведены формулы для оценок по результатам

испытаний нижних и верхних доверительных границ рассматри-

ваемых числовых характеристик с заданной доверительной веро-

ятностью α. Если необходимо ввести двусторонние доверитель-

ные границы, то названные формулы пригодны и для такого слу-

чая. При этом полагают вероятности выхода на верхнюю и ниж-

нюю границы одинаковыми и выражают α через заданное значе-

ние β. Так как (1 + α) + (1 - α) = (1 - β), то α = (1 + β)/2.

Невосстанавливаемые изделия. Наиболее распространен

случай, когда объем выработки меньше десятой части генераль-

196

ной совокупности. В этом случае для оценки нижней Р

и Р

гра-

ниц вероятности безотказной работы используют [4] биноми-

нальное распределение. При испытаниях n изделий доверитель-

ную вероятность 1 - α выхода на каждую из границ принимают

равной вероятности появления в одном случае не более m отказов,

в другом случае не менее m отказов:

∑

−

−=−

−

ini

1)1(

)!(!

; (11.3)

∑

−=−

−

ini

α1)1(

)!(!

. (11.4)

Пример 1. Оценить вероятность Р

при доверительной

вероятности α = 0,9, если испытано три изделия n = 3 и отказало

одно m = 1.

Решение. По формуле (11.3)

9,01)1(

321

−=−

⋅⋅

⋅

⋅⋅⋅

⋅

ннн

РРР

В итоге получаем Р

= 0,2.

В случае безотказных испытаний из

формулы (11.3) при m = 0 следует, что Р

связано с доверитель-

ной вероятностью и числом испытанных изделий выражением

∑

≠

−=−

−

ini

1)1(

)!(!

α .

Отсюда

Р α−= 1 .

197

Пример 2. n = 10; m = 0. Найти Р

Решение. 887,07,01

=−=

P .

При больших n и m формулами (11.3) и (11.4) неудобно

пользоваться. В этом случае прибегают к приближенным вычис-

лениям, заменяя биноминальное распределение нормальным с

использованием следующих рассуждений. Испытания n изделий

рассматриваем как испытания n выборок по одному изделию.

Результаты испытаний каждого изделия могут иметь два исхода:

= 0 – отказ и x

= 1 – изделие не отказало. По определению

среднее значение случайной величины равно сумме произведений

всех возможных значений СВ(в данном случае 0 и 1) на частоты

этих появлений. Поэтому

,10

Pxx

−

⋅+⋅=⋅=

∑

где Р

∗

– частость сохранения работоспособности. При больших n

частость стремится к вероятности Р. Среднеквадратическое от-

клонение S

случайной величины х при испытаниях одного изде-

лия составляет

)1()1()0()(

**2*2*2

PPxxS

iiix

−=













−

−+−=−=

∑

а по результатам испытаний n изделий оно в n раз меньше,

. Поэтому

)1(

−

. Предполагая в силу справедли-

198

вости центральной предельной теоремы распределения среднего,

как суммы, близким к нормальному , формулы для вычислений

нижней и верхней доверительных границ можно представить в

виде

)1(

uPSuРР

nxн

−

+=+=

αα

(11.6)

)1(

uPSuРР

nxв

−

+=−=

αα

(11.7

где u

– квантиль нормального распределения, соответствующая

выбранной доверительной вероятности α.

Приближение нормальным распределением используют,

если выполняются два условия: 10

>nP и .10)1(

>−Pn

Пример 3. Оценить Р

, Р

, если n = 100, m = 20, α = 0,95.

Решение. Вычисляем Р

= 0,8, nP

= 80 > 10; n(1-P

) = 20 > 10.

Следовательно, нормальное распределение можно использовать.

При α = 0,95 по табл. 4.1 распределения u

= -1,64. Отсюда

.0656,0−=

Поэтому Р

= 0,734, Р

= 0,866..1 для нормально-

го

Определим требуемый объем выборки n, если требуемая

вероятность безотказной работы равна Р

, заданы доверительный

интервал d = Р

- Р

и односторонняя доверительная вероятность

α. Предполагаем применимость нормального распределения.

Из формул (11.6), (11.7) следует, что

)1(

−

−=

а отсюда

199

**2

)1(4

PPu

−

. (11.8)

0,6 0,7 0,8

0,9

1,0

0,4

0,5

0,6

0,7

0,8

0,9

α=0,8

β=0,6

n=10

100

∞

100

0,6

0,7

0,8 0,9 1,0

0,4

0,5

0,6

0,7

0,8

0,9

α=0,9

β=0,8

n=10

100

∞

100

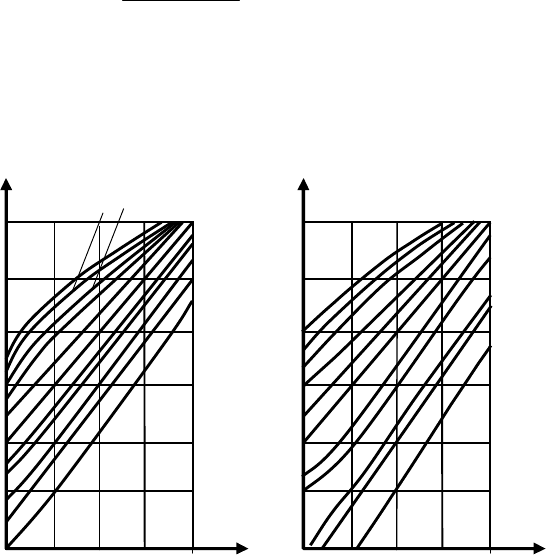
Рисунок 11.1 – График

зависимости нижней Р

верхней Р

доверительных

границ от объема и резуль-

татов испытаний при α =

0,8 и β = 0,6

Рисунок 11.2 – График

зависимости нижней Р

верхней Р

доверительных

границ от объема и резуль-

татов испытаний при α =

0,9 и β = 0,8

200

Пример 4. Оценить n, если P

= 0,8, Р

= 0,866, Р

= 0,73,

α = 0,95, d = Р

- Р

= 0,132; u

=-1,64; α = 0,95.

Решение. Подставляя в формулу (11.8) значения, получим

100

132,0

)8,01(8,064,14

≈

−⋅⋅

Формулы (11.3)...(11.7) позволили построить графики (рис.

11.1, 11.2, 11.3) зависимости нижней Р

и верхней Р

доверитель-

ных границ от числа n испытанных и m отказавших изделий Р

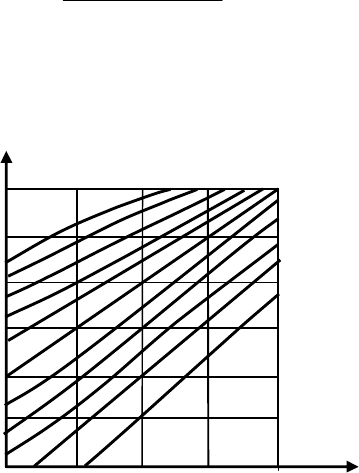
Рисунок 11.3 – График зависимости нижней Р

и верх-

ней Р

доверительных границ от объема и

результатов испытаний при α = 0,95 и β =

0,9

0,6

0,7

0,8

0,9

1,0

0,4

0,5

0,6

0,7

0,8

0,9

α=0,9

=0,8

n=1

∞