Козлов О.С., Скворцов Л.М., Ходаковский В.В. Решение дифференциальных и дифференциально-алгебраических уравнений в программном комплексе МВТУ
Подождите немного. Документ загружается.


Решение дифференциальных и дифференциально-алгебраических уравнений в программном комплексе
«МВТУ»
1
Козлов Олег Степанович
Скворцов Леонид Маркович
Ходаковский Виктор Владимирович
Решение дифференциальных и
дифференциально-алгебраических
уравнений в программном комплексе
«МВТУ»
Аннотация: Рассматриваются методы численного решения
обыкновенных дифференциальных уравнений (ОДУ) и
дифференциально-алгебраических уравнений (ДАУ),
реализованные в программном комплексе (ПК) «МВТУ».
Обсуждаются вопросы выбора метода и задания его
параметров при решении задач различного типа. Описаны
новые явные и неявные методы, эффективные для жестких
задач. Один из неявных методов позволяет также решать
системы ДАУ индексов 2 и 3. Приведены результаты
решения тестовых задач в сравнении с известными
методами
1. Введение
1. Общие положения
1. Постановка задачи
2. Параметры интегрирования
3. Управление шагом интегрирования
2. Явные методы
1. Классические методы
2. Модифицированные классические методы
3. Адаптивные методы
3. Неявные методы
1. Метод Гира
2. Адаптивный метод
3. Диагонально неявные методы Рунге-Кутты
4. Примеры решения тестовых задач
1. Жесткие задачи
2. Локально-неустойчивые задачи
5. Решение дифференциально-алгебраических уравнений (ДАУ)
1. Метод пространства состояний
2. Метод ε-вложения
3. Системы ДАУ высших индексов
6. Приложение
7. Литература и Интернет
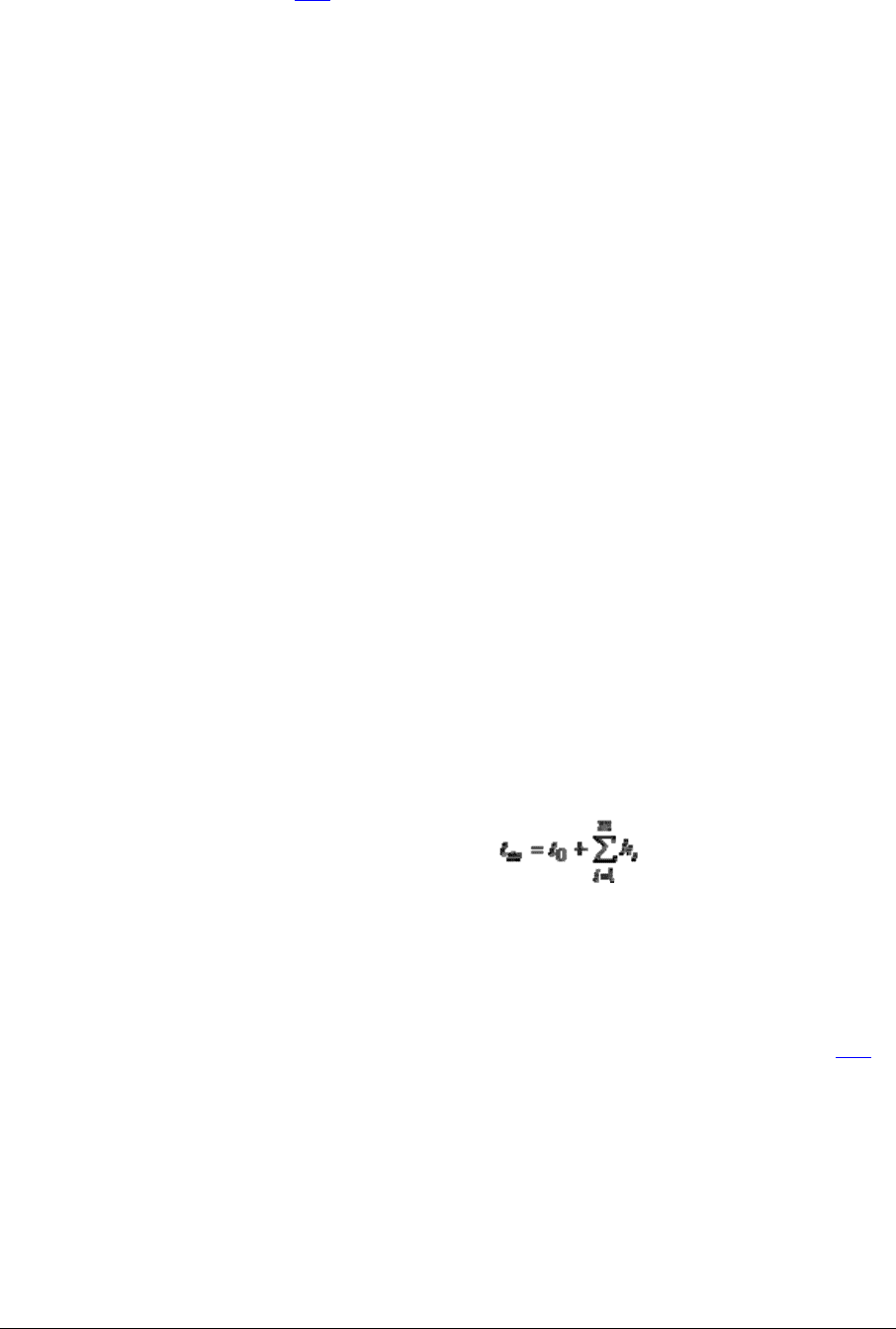
Решение дифференциальных и дифференциально-алгебраических уравнений в программном комплексе
«МВТУ»
2
Введение
В ПК «МВТУ» (версия 3.5) [1–3] реализованы 10 явных и 6 неявных методов численного
интегрирования (решателей ОДУ). Такой набор методов позволяет эффективно решать
самые различные задачи, но при этом возникает проблема выбора наиболее подходящего
метода и правильного задания его параметров. Очень часто пользователь задает только
интервал интегрирования и не обращает внимания на другие опции решателя. При
решении простых задач с умеренной точностью такой подход вполне допустим, однако
при решении сложных (например, жестких) задач неудачный выбор метода либо
неправильное задание его параметров может привести к неоправданно большим затратам
машинного времени либо к невозможности вообще получить правильное решение.
Таким образом, для профессиональной работы с любым моделирующим ПК пользователь
должен обладать некоторыми знаниями о реализованных в нем численных методах. Цель
настоящей статьи – дать пользователю необходимые сведения о решателях ПК «МВТУ».
Статья может быть полезной для пользователей и разработчиков других аналогичных ПК.
1. Общие положения
1.1. Постановка задачи
Моделирование процессов в непрерывных динамических системах сводится к численному
решению задачи Коши
(1.1)
x' = f(t, x), x(t
0
) = x
0
, t
0
≤ t ≤ (t
0
+ T),
где x – n-мерный вектор переменных состояния, f – n-мерная вектор-функция правых
частей, t – независимая переменная, T – величина интервала интегрирования. Численное
решение задачи (1.1) получаем в виде последовательности векторов x
m
, m = 1, 2, …
аппроксимирующих истинное решение на сетке , где h
i
– величина i-го шага
интегрирования.
Эффективность численного решения задачи Коши в значительной степени определяется
спектром матрицы Якоби системы ОДУ. Сложность задачи можно оценить величиной ρT,
где ρ – спектральный радиус матрицы Якоби. При умеренных значениях ρT (нежесткие
задачи) интегрирование обычно выполняется традиционными явными методами [4, 5] и
требует небольших вычислительных затрат. Трудности возникают при больших значениях
ρT, когда для получения правильного решения бывает необходимо выбирать очень малый
шаг интегрирования. В зависимости от расположения наибольших по модулю
собственных значений такие задачи подразделяются на жесткие (большие собственные
значения в левой полуплоскости), осциллирующие (вблизи мнимой оси) и локально-
неустойчивые
(в правой полуплоскости).
Практика показала, что реальные процессы, как правило, описываются жесткими
системами ОДУ. Достаточно часто в технических приложениях встречаются быстро

Решение дифференциальных и дифференциально-алгебраических уравнений в программном комплексе
«МВТУ»
3
осциллирующие системы, описывающие высокочастотные колебания, а также локально-
неустойчивые системы, в решении которых кратковременные участки с расходящимся
процессом чередуются с более продолжительными стабильными участками.
Перечисленные типы задач предъявляют совершенно разные требования к методам
интегрирования. При интегрировании жестких систем необходимо обеспечить быстрое
затухание жестких составляющих, для этого используют неявные A- или L-устойчивые
методы [4, 6]. Такие методы подавляют все составляющие решения, соответствующие
большим по модулю собственным значениям (если только шаг не выбран очень малым),
поэтому они плохо приспособлены для решения осциллирующих и локально-
неустойчивых систем. Для интегрирования осциллирующих систем следует применять
специальные методы, обеспечивающие правильный характер огибающей колебательного
решения. Специальные методы следует использовать также и для решения жестких
локально-неустойчивых систем.
Трудности возникают и при интегрировании систем с разрывами правой части. Для
правильного решения таких задач необходимо уменьшать шаг интегрирования в
окрестности точки разрыва, что предъявляет повышенные требования к процедуре
управления величиной шага.
Таким образом, для эффективного и качественно правильного решения задачи Коши
необходимо выявить характер задачи и выбрать наиболее подходящий метод.
Современные моделирующие ПК, как правило, содержат наборы методов, позволяющих
решать задачи разных типов. Однако характер задачи может изменяться в процессе
решения или при переходе от одной переменной к другой. Для решения таких задач могут
быть эффективными адаптивные методы [7, 8], расчетные формулы которых
настраиваются на решаемую задачу, используя для этого оценки некоторых параметров
(например, собственных значений якобиана). Особенно перспективны явные адаптивные
методы, не требующие при своей реализации вычисления матрицы Якоби и решения
алгебраических уравнений. Такие методы есть среди решателей ОДУ ПК «МВТУ».
1.2. Параметры интегрирования
Выбор метода и установка его параметров в ПК «МВТУ» осуществляется в диалоговом
окне «Параметры расчета». Это окно имеет 6 закладок, но только две из них (Основные и
Дополнительные) имеют отношение к методам интегрирования, а остальные позволяют
устанавливать различные режимы моделирования.
При открытии окна «Параметры расчета» активной является закладка Основные, где
задаются следующие параметры:
Метод интегрирования
Можно выбрать один из 16 методов (Эйлера, Рунге-Кутты классический, Рунге-
Кутты модифицированный, Мерсона классический, Мерсона модифицированный,
Адаптивный 1, …, Адаптивный 5, Адаптивный неявный, Диагонально неявный,
Гира, Неявный Эйлера, DIRK33, DIRK44). По умолчанию используется
Адаптивный 1. Метод Эйлера может иметь только фиксированный шаг, а все
остальные методы могут использоваться как с фиксированным, так и с переменным
шагом.
Время интегрирования T
Длительность интервала модельного времени, на котором выполняется
моделирование (по умолчанию 10).

Решение дифференциальных и дифференциально-алгебраических уравнений в программном комплексе
«МВТУ»
4
Минимальный шаг интегрирования hmin
Этот параметр ограничивает снизу шаг интегрирования и по умолчанию равен 10
-6
.
Если значение hmin оказывается недостаточно малым для расчета с заданной
точностью, то выдается сообщение «Заданная точность не обеспечивается». В
таких случаях следует уменьшить минимальный шаг либо снизить требования к
точности. Уменьшение значения hmin обычно мало сказывается на времени счета,
однако нежелательно задавать этот параметр меньше 10
-15
T.
Максимальный шаг интегрирования hmax
Ограничение сверху на шаг интегрирования, а для метода Эйлера – величина шага
(по умолчанию 0.1). Если задать hmax = hmin, то интегрирование будет
выполняться с фиксированным шагом. Слишком малое значение hmax приводит к
неоправданному увеличению времени счета, а большое значение может привести к
уменьшению числа точек, выводимых на график. Рекомендуемое значение – T /100.
Шаг вывода результатов dT
Приблизительное значение шага вывода результатов в графические окна, при этом
реальный шаг вывода не может быть меньше шага интегрирования. Точное
значение заданного шага вывода будет соблюдаться, если установить (на закладке
Дополнительные) табуляцию результатов расчета. Рекомендуется задавать
dT = (10
-3
…10
-2
)×T. При dT = 0 результаты выводятся на каждом шаге
интегрирования. Аналогичного эффекта для отдельного графического окна можно
добиться, установив в окне свойств соответствующего блока: Вывод на каждом
шаге – Да; Прореживание точек – Нет.
Точность Rtol
Допустимая относительная ошибка интегрирования (по умолчанию 0.001). Не
рекомендуется задавать это значение больше 0.01 или меньше 10
-10
.
На закладке Дополнительные устанавливаются следующие параметры:
Значения выходов при инициализации
Начальные значения алгебраических переменных при наличии в системе
алгебраических контуров (по умолчанию 10
-10
). Для каждой переменной можно
установить свое значение, если включить в контур блок Y = F(Y).
Абсолютная ошибка Atol
Допустимая абсолютная ошибка интегрирования (по умолчанию 10
-10
). Ненулевое
значение Atol предотвращает неоправданное уменьшение шага в тех случаях, когда
значения некоторых переменных приближаются к нулю.
Максимальное значение производных (по умолчанию 10
300
)
Если производная некоторой переменной превышает по модулю это значение или
произошла фатальная ошибка (переполнение, деление на 0 и т.д.), то шаг считается
неудачным. После этого интегрирование возобновляется с уменьшенным шагом
либо прекращается с выдачей сообщения об ошибке, если размер шага достиг hmin.
Метод итерирования для петель
Метод решения алгебраических уравнений при наличии в системе алгебраических
контуров (Простая итерация – по умолчанию, Ньютона-Рафсона, Бройдена
(секущих), Без итераций). Выбранный метод используется для расчета начального
состояния алгебраических переменных (независимо от метода интегрирования), а
также для расчета алгебраических переменных в процессе интегрирования явным
методом. В процессе интегрирования неявным методом дифференциальные и
алгебраические переменные решаются совместно, поэтому выбор метода
итерирования не имеет значения. Наиболее надежным является метод Ньютона-
Рафсона, но в некоторых случаях и другие методы могут иметь преимущество.
Число итераций

Решение дифференциальных и дифференциально-алгебраических уравнений в программном комплексе
«МВТУ»
5
Максимальное число итераций при решении алгебраических уравнений (по
умолчанию 20). Этот параметр, как и предыдущий, влияет на решение только в тех
случаях, когда в системе есть алгебраические контуры или блоки Y = F(Y),
F(Y) = 0.
Табуляция результатов расчета
Установив этот флаг, мы добьемся вывода результатов на графики с шагом, в
точности равным заданному шагу вывода. Этот флаг рекомендуется также
устанавливать при наличии в системе дискретных блоков, тогда шаг вывода
следует устанавливать таким, чтобы периоды квантования дискретных блоков
были равны или кратны ему. Если табуляция установлена, то шаг интегрирования
не может превышать шага вывода результатов.
1.3. Управление шагом интегрирования
Начальный шаг устанавливается равным . В процессе интегрирования с
переменным шагом необходимо, кроме решения в очередной точке, вычислять оценку
ошибки, которая используется для управления величиной шага. Для этого применяют две
различные формулы интегрирования, дающие на m-м шаге два решения: x
m
и . Пусть
x = x
m
– вектор переменных, Δx = x
m
- x
m-1
– приращение, δx = x
m
- – оценка ошибки на
последнем шаге. Для управления величиной шага используется нормированная ошибка,
вычисляемая по формуле
(1.2)
,
причем шаг считается удачным, если err ≤ 1. В случае удачного шага принимаем значение
x
m
в качестве нового вектора переменных. При неудачном шаге производится пересчет с
уменьшенным размером шага. Шаг считается неудачным также и в том случае, когда одна
из производных превысила максимально допустимое значение, задаваемое в окне
«Параметры расчета», либо произошло прерывание, вызванное переполнением, делением
на ноль, недопустимым значением аргумента и т.п. В
таких случаях размер шага
уменьшается сразу в 4 раза, но если он стал меньше hmin, то моделирование прекращается
и выдается сообщение об ошибке.
Особенностью ПК "МВТУ" и аналогичных систем моделирования является то, что
вычисление правой части системы ОДУ (1.1) осуществляется одновременно с расчетом
всей модели. При этом некоторые блоки модели рассчитываются только на
заключительной стадии удачного шага. К таким блокам относятся дискретные, ключи, а
также некоторые логические блоки. Это сделано с целью исключения внутри шага
разрывов производной, которые могут привести к неоправданному уменьшению шага и
возникновению «скользящего режима».
В большинстве методов, реализованных в ПК «МВТУ», используется стандартная
процедура управления величиной шага [6], задаваемая формулой
(1.3)
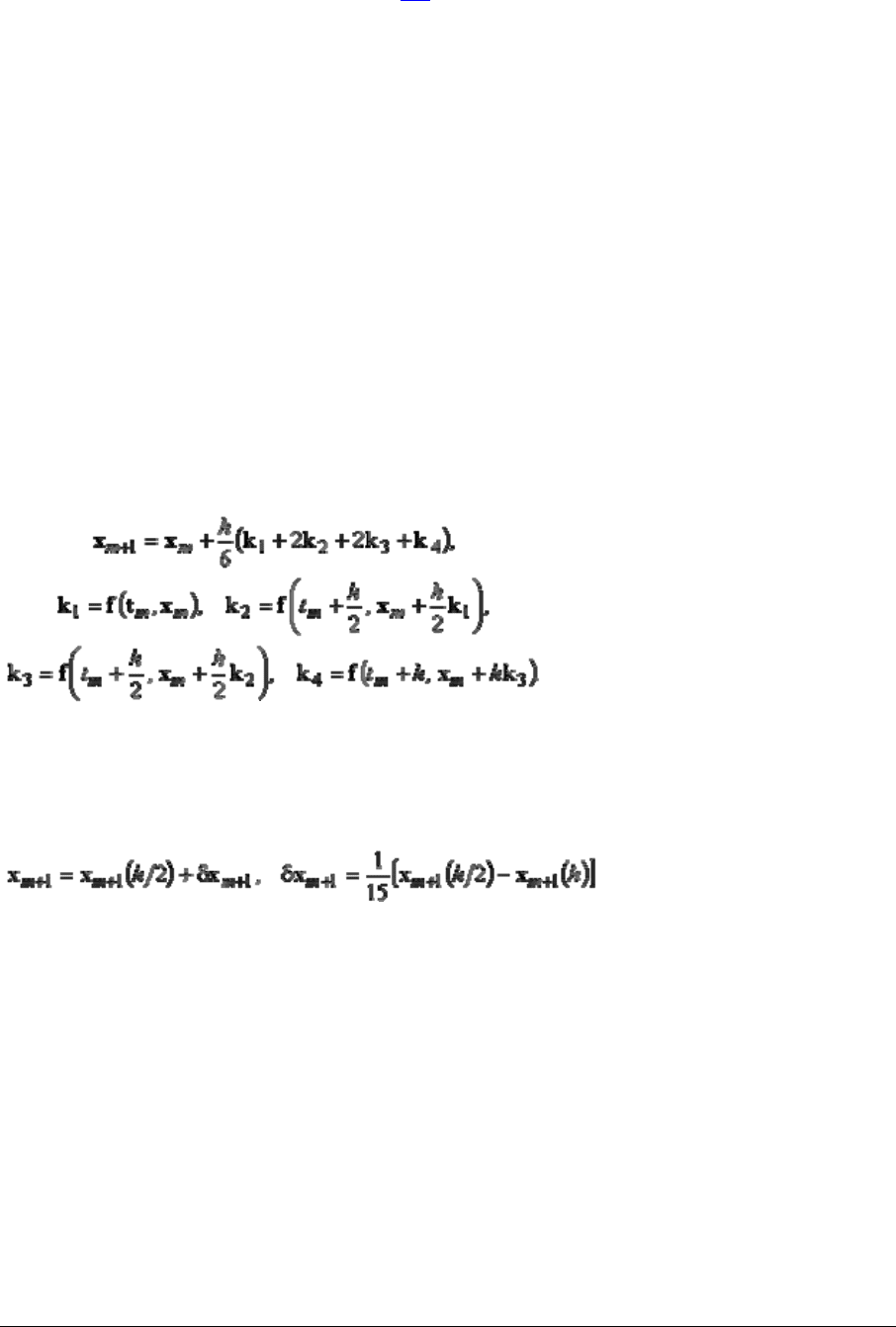
Решение дифференциальных и дифференциально-алгебраических уравнений в программном комплексе
«МВТУ»
6
h
m+1
= fac · h
m
· err
-α
,
где fac = 0.8…0.9 – множитель безопасности, α – величина, обратная порядку оценки
ошибки, err – нормированная ошибка (1.2).
2. Явные методы
Явные методы представлены в ПК «МВТУ» методом Эйлера, классическими и
модифицированными методами Рунге-Кутты и Мерсона, а также пятью адаптивными
методами.
2.1. Классические методы
Метод Эйлера является простейшим, имеет 1-й порядок и задается расчетной формулой
x
m+1
= x
m
+ h f(t
m
, x
m
).
Его можно использовать при интегрировании с постоянным шагом и низкой точностью.
Классический метод Рунге-Кутты задается формулами
Он имеет 4-й порядок, однако, применяя экстраполяцию по Ричардсону, можно повысить
порядок до 5-го, получив дополнительно оценку ошибки. Окончательные расчетные
формулы имеют вид
,
где δx
m+1
– оценка ошибки, а x
m+1
(h) и x
m+1
(h / 2) – численные решения, полученные,
соответственно, путем выполнения одного шага размера h и двух шагов размера h / 2.
Отметим, что такой метод требует довольно значительных вычислительных затрат,
поскольку на каждом шаге функция f вычисляется 11 раз.
Метод Мерсона имеет 4-й порядок и задается формулами

Решение дифференциальных и дифференциально-алгебраических уравнений в программном комплексе
«МВТУ»
7
По сравнению с классическим методом Рунге-Кутты, в методе Мерсона используется
более экономный способ оценивания ошибки и управления величиной шага.
При решении умеренно жестких задач явными методами размер шага обычно
приближается к границе устойчивости, но в этом случае процедура управления шагом
может оказаться неустойчивой. В результате происходят резкие колебания величины
шага, приводящие к снижению точности и увеличению вычислительных затрат.
Устойчивость управления шагом (SC-устойчивость [6]) можно обеспечить при
использовании процедуры ПИ-управления [6
], задаваемой формулой
(2.1)
h
m+1
= fac · h
m
· (err
m
)
-α
· (err
m-1
)
β
,
где коэффициент β выбирается из условия SC-устойчивости (обычно 0 ≤ β ≤ 0.1). При
β = 0 получаем стандартную процедуру (1.3). Для метода Мерсона выбраны значения
α = 0.2, β = 0.08, обеспечивающие SC-устойчивость. Эксперименты показали, что
использование ПИ-закона (2.1) позволяет снизить затраты и повысить точность решения
умеренно жестких задач по сравнению с использованием стандартной процедуры (1.3).
Классические методы рекомендуется использовать для решения нежестких задач.
2.2. Модифицированные классические методы
Классические методы неэффективны при решении жестких задач, однако несложная
модификация расчетных схем может расширить область их применения, позволяя
эффективно решать как нежесткие, так и умеренно жесткие задачи [7]. В
модифицированных методах на основе предварительных стадий вычисляются
покомпонентные оценки наибольшего собственного значения матрицы Якоби, которые
используются для стабилизации расчетной схемы. В приведенных ниже формулах все
действия с векторами выполняются покомпонентно.
Модифицированный метод Рунге-Кутты отличается от классического способом
вычисления k
4
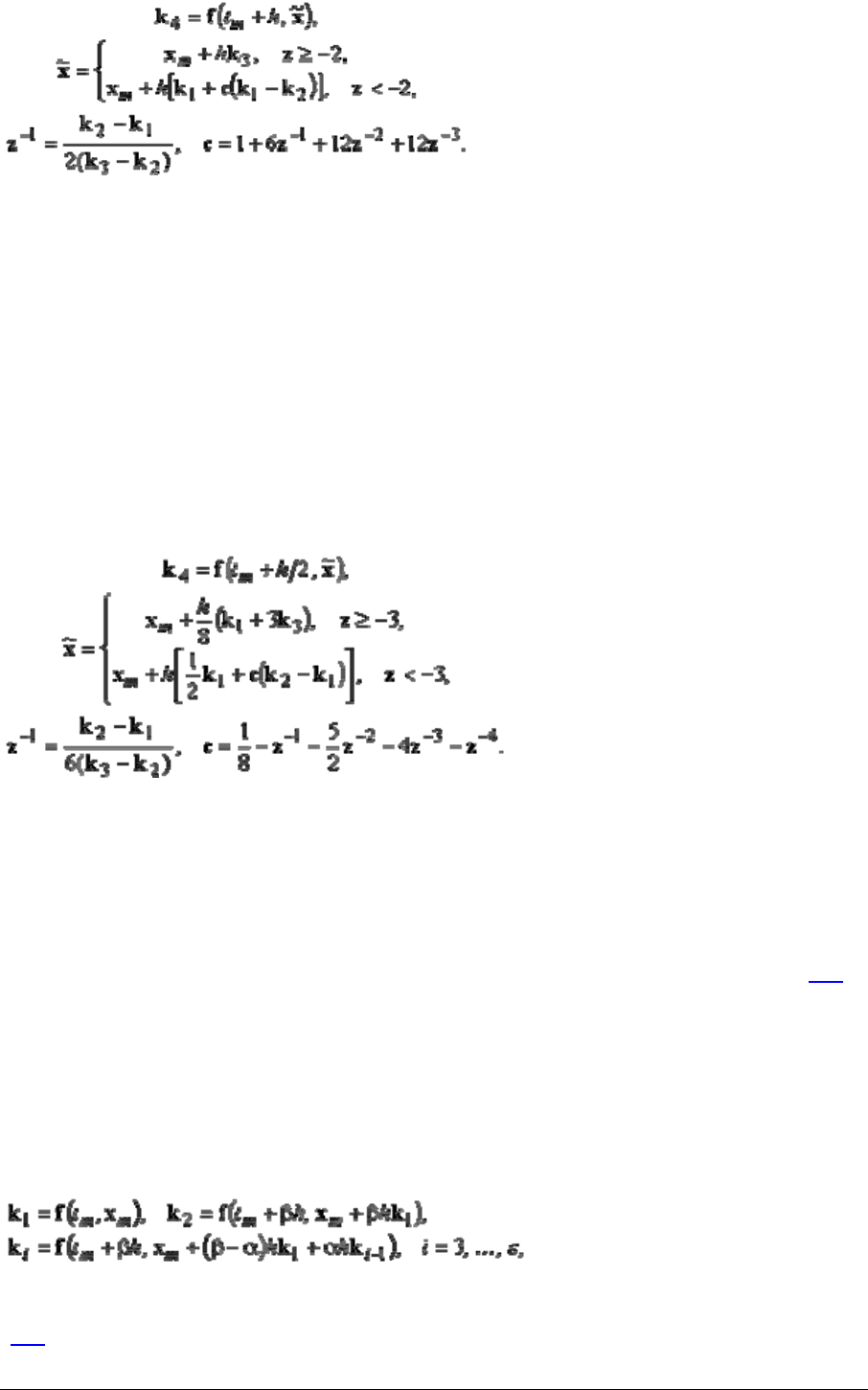
Решение дифференциальных и дифференциально-алгебраических уравнений в программном комплексе
«МВТУ»
8
Здесь z – вектор покомпонентных оценок наибольшего по модулю собственного значения
матрицы hJ, где J – матрица Якоби. В приведенных формулах покомпонентно
выполняются не только арифметические, но и логические операции. При проверке
выполнения неравенств компоненты вектора z не вычисляются, а вместо этого
вычисляются и сравниваются компоненты векторов k
2
- k
1
и k
3
- k
2
. Для нежестких
компонент, т.е. при выполнении условия z
i
≥ -2 применяется классическая формула, а для
жестких компонент – формула, полученная из условия стабилизации метода в полученной
точке жесткого спектра, причем вычисляются и используются только компоненты вектора
z
-1
, удовлетворяющие условию -0.5 < z
i
-1
< 0.
Модифицированный метод Мерсона также отличается от классического способом
вычисления k
4
:
Модифицированные методы рекомендуется использовать для решения умеренно жестких
задач с повышенной точностью.
2.3. Адаптивные методы
Значительно более эффективны при решении жестких задач адаптивные методы [7, 8],
основанные на получении оценок наибольших по модулю собственных значений и
последующей стабилизации расчетной схемы в полученных точках жесткого спектра.
Одношаговые адаптивные методы строятся на основе стадий Рунге-Кутты, которые
выполняются по формулам
(2.2)
где s – число стадий, β и α – параметры метода (в общем случае самонастраиваемые
[7, 8]). Далее вычисляются векторы

Решение дифференциальных и дифференциально-алгебраических уравнений в программном комплексе
«МВТУ»
9
(2.3)
,
которые используются для получения оценок собственных значений и в заключительной
формуле шага интегрирования.
Вектор покомпонентных оценок наибольшего собственного значения получим в виде
(2.4)
z = y
s
/ y
s-1
.
С помощью этих оценок вычисляется вектор настраиваемых параметров с, который
используется в формуле шага интегрирования
(2.5)
.
Из (2.5) видно, что порядок метода для жестких задач не может превышать s - 2. На основе
формул (2.2)–(2.5) построены одношаговые методы Адаптивный 1, 2, 3, 5.
Адаптивный 1 – трехстадийный метод (s = 3), имеет 1-й порядок для жестких и 2-й для
нежестких задач. В нем β = 1, тогда вектор (2.4) получим в виде z = (k
3
- k
2
) / [α (k
2
- k
1
)].
Компоненты вектора настраиваемых параметров вычисляются по формуле
,
а формула (2.5) принимает вид x
m+1
= x
m
+ h k
1
+ h c (k
2
- k
1
). Ошибка оценивается с
помощью двухшаговой формулы
где ω = h
m+1
/ h
m
– отношение текущего шага к предыдущему, d
i
= -z
i
c
i
, i = 1, …, n. Для
очень жестких компонент выполняются одна или две дополнительные стадии,
расширяющие область устойчивости в окрестности точек жесткого спектра.
Адаптивный 2 – расчетная схема аналогична методу Адаптивный 1, но дополнительные
стадии не используются, а значение β изменяется от 2/3 до 1 в зависимости от жесткости
задачи, благодаря чему порядок метода для нежестких задач повышается до 3-го. Ошибка
оценивается по правилу Рунге, т.е. с использованием одного шага размера h и двух шагов
размера h / 2.
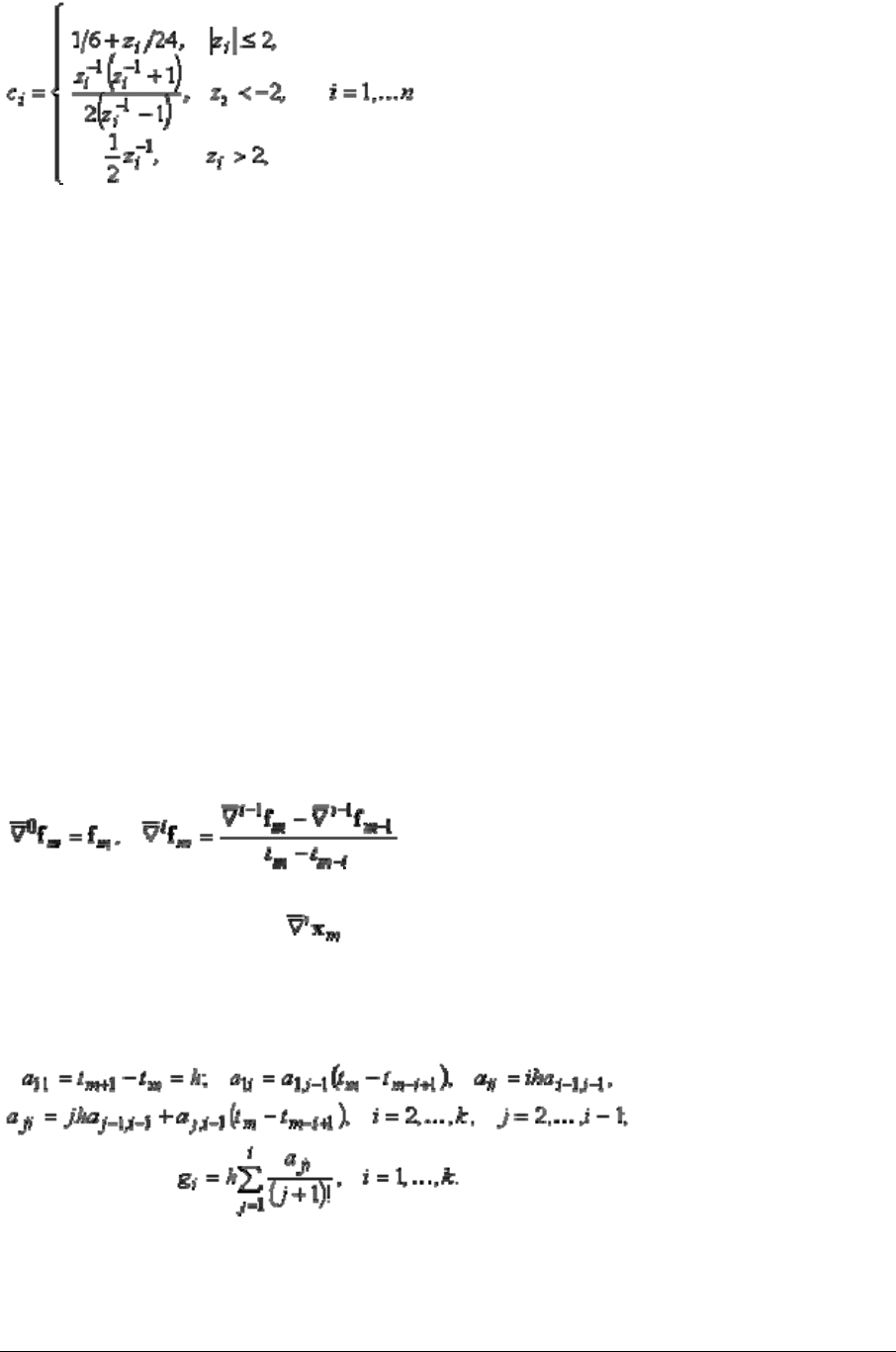
Решение дифференциальных и дифференциально-алгебраических уравнений в программном комплексе
«МВТУ»
10
Адаптивный 3 – четырехстадийный метод (s = 4) 2-го порядка для жестких и 3-го для
нежестких задач. Вектор настраиваемых параметров вычисляется по формуле
.
Для оценивания ошибки используется вложенная формула.
Адаптивный 5 – пятистадийный метод 2-го порядка для жестких и 3-го для нежестких
задач, шаг которого выполняется по формуле
x
m+1
= x
m
+ h (y
1
+ d
2
y
2
+ d
3
y
3
).
Векторы настраиваемых коэффициентов d
2
, d
3
вычисляются с использованием
покомпонентных оценок двух наибольших собственных значений, которые могут быть
как вещественными, так и комплексными. Благодаря этому метод эффективен также и при
решении осциллирующих задач.
Одношаговые адаптивные методы имеют невысокую точность, поэтому в ПК «МВТУ»
реализован также многошаговый метод. На многих жестких задачах он оказался наиболее
эффективным среди
всех адаптивных методов. Поскольку этот метод нигде не описан,
рассмотрим его более подробно.
Адаптивный 4 – многошаговый адаптивный метод переменного порядка (1…5 для
жестких и 2…6 для нежестких задач), основанный на использовании разделенных
разностей, определяемых рекуррентно согласно формулам
.
(аналогично определяются ). Введем также коэффициенты a
ij
, g
i
, зависящие от
размеров текущего и предыдущих шагов и задаваемые формулами
(2.6)
В этом случае k-шаговые формулы прогноза и коррекции при интегрировании с
переменным шагом запишутся в виде
