Козлов О.С., Скворцов Л.М., Ходаковский В.В. Решение дифференциальных и дифференциально-алгебраических уравнений в программном комплексе МВТУ
Подождите немного. Документ загружается.


Решение дифференциальных и дифференциально-алгебраических уравнений в программном комплексе
«МВТУ»
11
(2.7а)
,
(2.7б)
,
где – разделенная разность с использованием вместо f
m+1
. Формула прогноза
имеет порядок k, а порядок формулы коррекции на 1 больше.
На основе формул вида (2.7) обычно строят многошаговые методы Адамса переменного
порядка и шага [4, 5], при этом , а оценка ошибки находится как разность
между прогнозом и скорректированным решением. Для адаптивного метода эти формулы
являются предварительными, на их основе получаем вектор оценок наибольшего
собственного значения . Вместо него вычисляем вектор
(2.8)
,
причем только для жестких и неустойчивых компонент, удовлетворяющих условию
, где μ - константа, определяемая областью устойчивости и
зависящая от k. Формула интегрирования для таких компонент имеет вид
(2.9)
,
где векторные коэффициенты d
i
вычисляются по формулам
(2.10)
(e – n-мерный вектор с единичными компонентами). Формула (2.9) построена таким
образом, что она имеет порядок k и обеспечивает затухание за один шаг при решении
уравнения x' = λ x, λ < 0.

Решение дифференциальных и дифференциально-алгебраических уравнений в программном комплексе
«МВТУ»
12
Формулы (2.6)–(2.10) задают многошаговый адаптивный метод с переменным шагом, при
этом для нежестких компонент ограничиваемся формулами (2.7), а дальнейшие
вычисления не производим. Оценку ошибки получаем как приращение в формуле
коррекции (2.7б) для нежестких компонент или последний член в формуле (2.9) для
жестких компонент. Приведенные формулы позволяют также легко изменять порядок
метода, который определяется значением k. Если на предыдущем шаге k = k
old
, то на
очередном шаге значение k может быть от 1 до k
old
+ 1. Новое значение k определяется на
этапе прогноза исходя из условия, чтобы прогноз был наиболее точным. Формулу
прогноза (2.7а) можно записать в виде
.
Новое значение k определяется как максимальное число, для которого выполняется
условие
|| δ
1
|| > || δ
2
|| > … > || δ
k
||,
где норма ошибки вычисляется в соответствии с (1.2).
3. Неявные методы
При решении многих жестких задач явные адаптивные методы показали результаты,
сравнимые с неявными методами, однако наиболее универсальным средством решения
жестких задач все-таки остаются неявные методы.
3.1. Метод Гира
Метод Гира – многошаговый метод переменного порядка (от 1-го до 6-го), построенный
на основе формул дифференцирования назад (ФДН) [4–6] вида
,
где коэффициенты a
1
, …, a
k
, b зависят от порядка формулы k. В методе Гира эти формулы
реализованы с помощью вектора Нордсика [4, 5
], позволяющего использовать
эффективный алгоритм автоматического изменения порядка и величины шага. Последние
компоненты вектора Нордсика позволяют получить оценку ошибки. При k = 1 (тогда
a
1
= b = 1) получим неявный Эйлера – метод 1-го порядка, реализованный в ПК
«МВТУ».
3.2. Адаптивный метод
Адаптивный неявный метод имеет порядок от 2-го для жестких до 4-го для нежестких
задач; он построен на основе метода трапеций, формула которого имеет вид
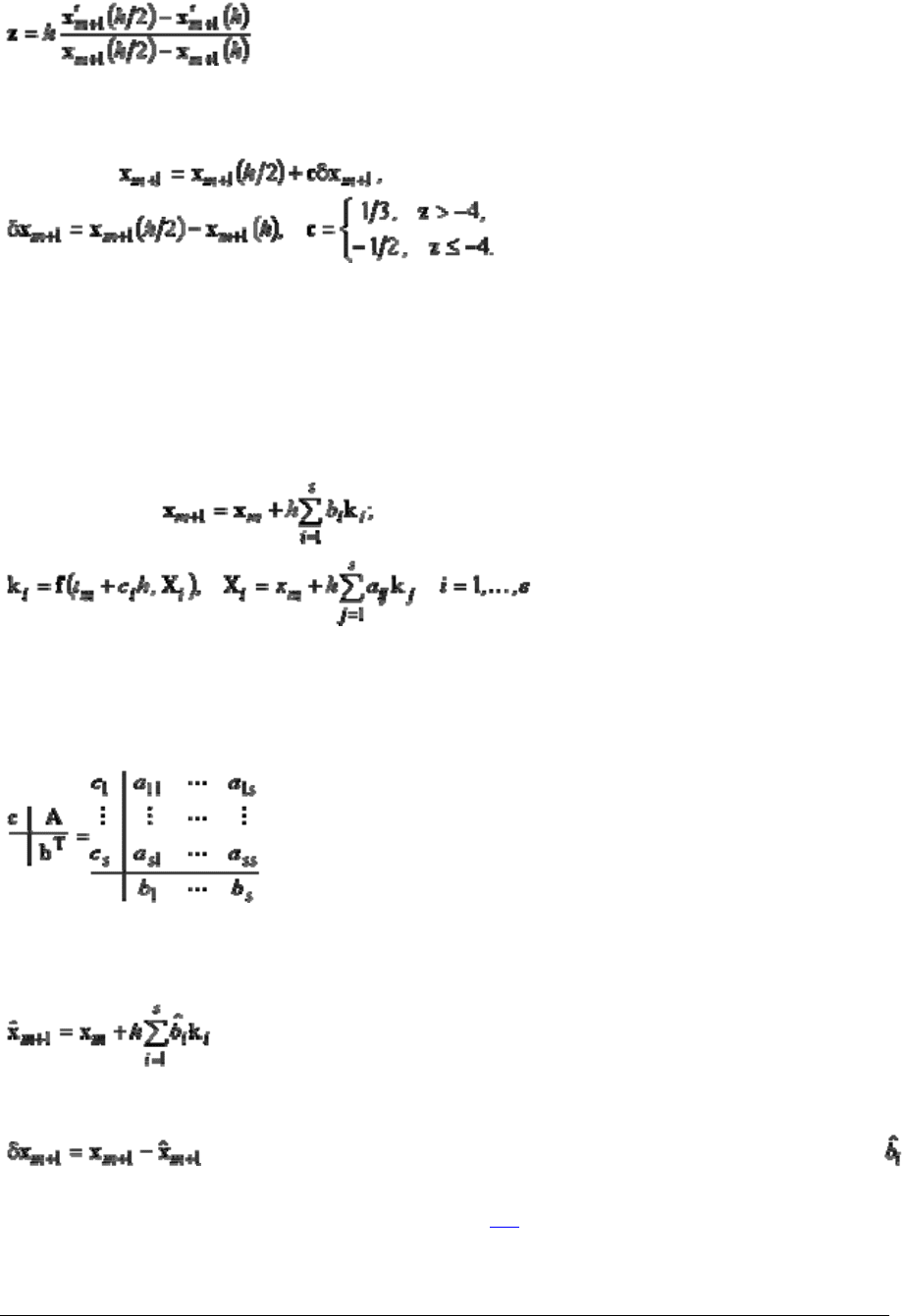
Решение дифференциальных и дифференциально-алгебраических уравнений в программном комплексе
«МВТУ»
13
Выполняя один шаг величиной h, получим x
m+1
(h), а выполняя два шага величиной h / 2,
получим x
m+1
(h / 2). Далее вычисляем вектор покомпонентных оценок наибольшего
собственного значения
,
который используется в заключительной расчетной формуле
3.3. Диагонально неявные методы Рунге-Кутты
В общем случае метод Рунге-Кутты задается формулами
(3.1)
и может быть представлен в виде таблицы Бутчера
(3.2)
.
Часто приводят также формулу
,
которая используется для получения оценки погрешности численного решения
. В этом случае в таблицу (3.2) добавляется строка коэффициентов .
В явном методе a
ij
= 0 при j ≥ i, тогда формулы (3.1) задают расчетный алгоритм, который
может быть непосредственно реализован. В противном случае метод является неявным и
требует при своей реализации решения системы алгебраических уравнений. Среди
неявных методов Рунге-Кутты наиболее просто реализуются диагонально неявные (DIRK
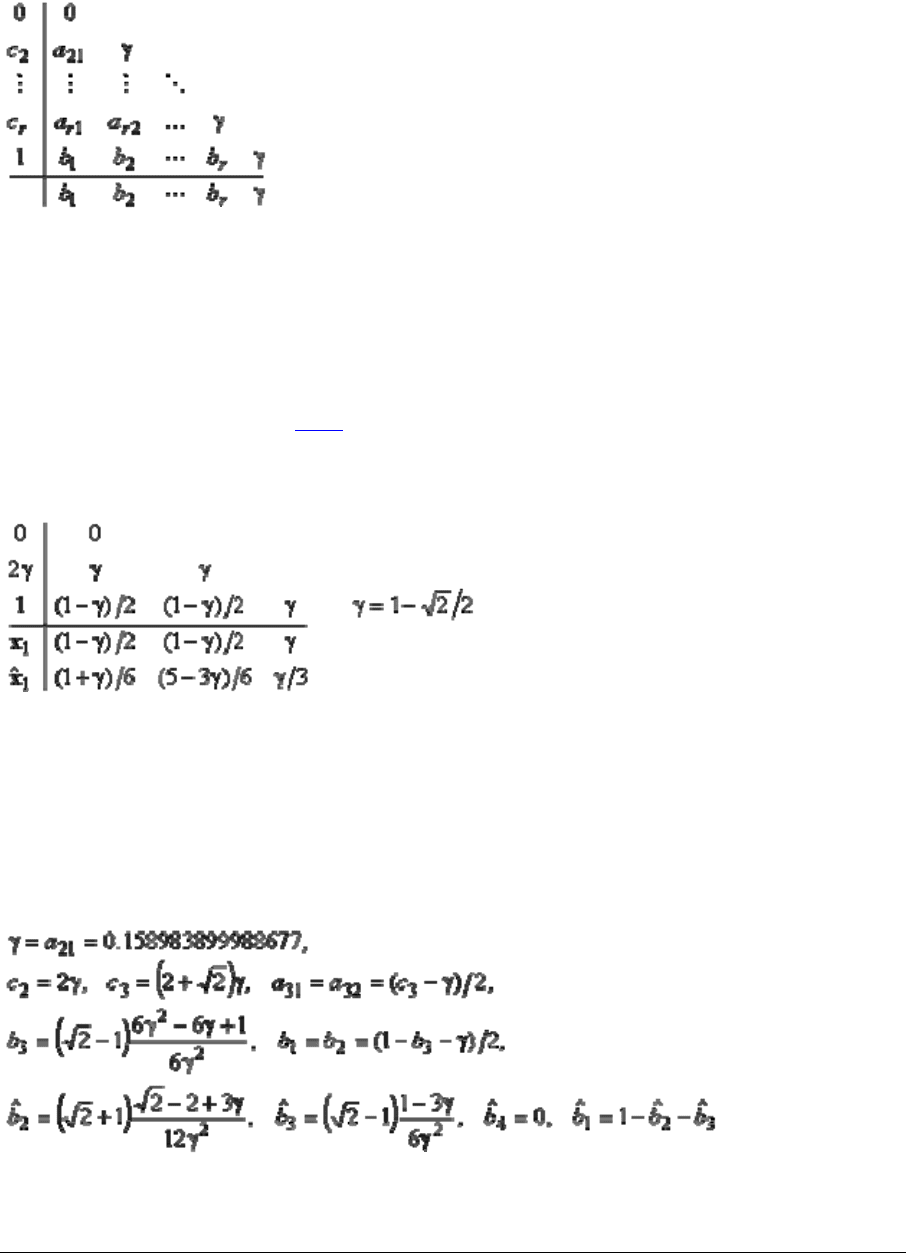
Решение дифференциальных и дифференциально-алгебраических уравнений в программном комплексе
«МВТУ»
14
– Diagonally Implicit Runge-Kutta), у которых матрица A имеет нижнюю треугольную
форму.
В ПК «МВТУ» реализованы три метода DIRK, имеющие таблицу Бутчера вида
(3.3)
Эти методы имеют явную первую стадию и r = s -1 неявных стадий с одинаковыми
диагональными элементами матрицы A, поэтому их обычно называют ESDIRK (Explicit
first stage Singly DIRK). Явная стадия не требует вычислений, поскольку результат ее
выполнения совпадает с последней стадией предыдущего шага. Такие методы называют
также FSAL (First Same As Last). Преимущество методов вида (3.3) по сравнению с
другими методами DIRK состоит в том, что они являются жестко точными и могут иметь
второй стадийный порядок [9, 10].
Диагонально неявный – метод 2-го порядка, задаваемый таблицей Бутчера
.
Его можно интерпретировать как последовательное применение правила трапеций и
формулы дифференцирования назад 2-го порядка, поэтому он получил название TR-
BDF2. Этот метод реализован также и в системе MATLAB+Simulink под названием
ode23tb.
DIRK33 – метод 3-го порядка с 3-мя неявными стадиями и коэффициентами
DIRK44 – метод 4-го порядка с 4-мя неявными стадиями и коэффициентами

Решение дифференциальных и дифференциально-алгебраических уравнений в программном комплексе
«МВТУ»
15
Методы DIRK33, DIRK44 и еще три аналогичных метода 4-го и 5-го порядков
предложены в [9], где изложены также детали их реализации.
4. Примеры решения тестовых задач
Решатели ОДУ ПК «МВТУ» были испытаны на множестве разнообразных задач, среди
которых – задачи из тестовых наборов, приведенных в [5, 6, 11]. Результаты тестовых
испытаний в сравнении с решателями системы MATLAB представлены в [12
] и в
Приложении
. Среди задач были нежесткие, жесткие, локально-неустойчивые,
осциллирующие, а также задачи с разрывами. Оценивались точность решения и
вычислительные затраты. Нежесткие задачи оказались самыми легкими и были успешно
решены всеми методами с автоматическим выбором шага. Поэтому остановимся на
жестких задачах, численное решение которых часто встречает затруднения.
4.1. Жесткие задачи
Посмотрим, как влияет жесткость задачи на точность ее решения и вычислительные
затраты. Будем решать задачу Капса
x'
1
= -(μ + 2) x
1
+ μ x
2
2
, x
1
(0) = 1,
x'
2
= x
1
- x
2
- x
2
2
, x
2
(0) = 1, 0 ≤ t ≤ 1,
которая имеет плавное решение x
1
(t) = exp(-2t), x
2
(t) = exp(-t), не зависящее от параметра
жесткости μ (собственные значения якобиана при больших μ примерно равны – μ, –1). В
качестве меры вычислительной работы будем использовать число вычислений правой
части Nf (включая также и вычисления, выполняемые при расчете матрицы Якоби), а
точность численного решения будем оценивать по формуле
(4.1)
scd = – log10 (error),
где error
– максимальная относительная ошибка на всем интервале интегрирования.
Таким образом, scd – минимальное число правильных значащих цифр численного
решения (significant correct digits). Результаты для явных методов и трех лучших неявных
методов при hmin = 10
-6
, hmax = 1, Rtol = 10
-3
, Atol = 10
-10
приведены в табл.1.
Таблица 1. Точность и вычислительные затраты при решении задачи Капса

Решение дифференциальных и дифференциально-алгебраических уравнений в программном комплексе
«МВТУ»
16
Метод
μ = 10
1
scd Nf
μ = 10
2
scd Nf
μ = 10
3
scd Nf
μ = 10
4
scd Nf
μ = 10
5
scd Nf
Рунге-Кутты кл.
Рунге-Кутты мод.
Мерсона
Мерсона мод.
3.7 110
3.7 110
4.9 100
4.9 100
4.1 264
3.6 198
4.5 250
4.5 250
0.4 2639
3.3 528
3.8 1419
4.4 835
-0.7 25770
3.1 605
3.9 14098
3.9 4133
-1.9 255720
3.4 1210
4.1 140902
3.1 19715
Адаптивный 1
Адаптивный 2
Адаптивный 3
Адаптивный 4
Адаптивный 5
4.0 87
3.8 120
3.7 75
5.0 42
4.3 120
3.6 143
3.7 208
3.5 125
5.6 48
3.6 217
2.7 237
2.2 248
3.4 150
5.6 51
3.9 260
2.1 304
2.0 256
3.4 165
5.5 60
3.9 270
2.0 319
1.8 240
3.6 195
5.5 60
3.9 270
Гира
DIRK33
DIRK44
2.9 39
2.6 36
4.0 55
3.1 40
3.0 49
4.0 53
3.1 40
3.3 34
4.2 47
3.0 40
3.3 34
3.6 41
3.0 40
3.3 34
3.6 41
Вычислительных затраты классических явных методов возрастают практически линейно
при увеличении жесткости, что вызвано необходимостью уменьшать шаг интегрирования
для обеспечения устойчивости численного решения. Значительное снижение точности
классического метода Рунге-Кутты объясняется отсутствием SC-устойчивости.
Модифицированные методы эффективнее классических, но заметно уступают адаптивным
и неявным методам. Адаптивные методы демонстрируют небольшое увеличение объема
вычислений при
повышении жесткости (а первые два из них также и снижение точности),
что вызвано снижением порядка при решении жестких задач. Точность и вычислительные
затраты неявных методов практически не зависят от жесткости. Результаты решения
задачи Капса подтвердили эффективность метода Гира, который традиционно считается
одним из лучших для жестких задач, а также показали перспективность новых методов
(адаптивных, DIRK33, DIRK44).
Для более полного тестирования жестких решателей ПК «МВТУ» и системы MATLAB
были выбраны первые шесть задач из тестового набора, приведенного в [6] (VDPOL,
ROBER, OREGO, HIRES, E5, PLATE). Результаты приведены в [12] и в Приложении. С
приемлемыми затратами и точностью решили все шесть задач четыре решателя ПК
«МВТУ» (Диагонально неявный, Гира, DIRK33, DIRK44) и два решателя системы
MATLAB (ode15s и ode23tb). В [12] приведен график зависимости суммарных
вычислительных затрат от усредненной по всем задачам точности для этих решателей.
Лучшие результаты – у методов Гира, DIRK33, DIRK44 и ode15s, при этом методы Гира и
ode15s имеют небольшое преимущество при расчетах с высокой точностью, а решатели
DIRK33 и DIRK44 при той же задаваемой точности обеспечивают, как правило, более
высокую точность. Отметим, что явный решатель Адаптивный 4 оказался лучшим среди
всех методов при решении жесткого уравнения Ван-дер-Поля (задача VDPOL).
Приведем также результаты сравнения решателей ПК «МВТУ» с решателем RADAU,
реализующим методы Radau IIa порядков 5, 9 и 13 [6, 11]. По результатам тестирования
наиболее известных программ этот решатель был лучшим для большинства задач из [11].
Мы выбрали задачи VDPOL и OREGO, которые решали при Rtol = Atol = 10
-4
согласно
условиям, приведенным в [11]. Из этой же работы заимствованы результаты для RADAU
(tables II.8.4, II.9.3 в [11
]). Полученные результаты представлены в табл. 2.
Вычислительные затраты оценивались следующими показателями: Nf – число вычислений
функции (сюда не включены вычисления, выполняемые при расчете якобиана); NJac –
число вычислений якобиана; NLU – число LU-разложений. При вычислении scd по
формуле (4.1
) использовалась максимальная относительная ошибка в конце интервала

Решение дифференциальных и дифференциально-алгебраических уравнений в программном комплексе
«МВТУ»
17
интегрирования. Отметим высокую эффективность явного адаптивного метода, который
показывает превосходные результаты также и при решении других жестких задач
(например, задачи CUSP из [6], имеющей 96-й порядок и 32 жестких собственных
значения). Таким образом, явные адаптивные методы могут успешно конкурировать с
лучшими неявными методами при решении многих жестких задач.
Таблица 2. Точность и вычислительные затраты при решении двух жестких задач
Задача Метод
scd Nf NJac NLU
VDPOL
Адаптивный 4
Гира
DIRK33
DIRK44
RADAU
4.11
3.39
3.99
4.08
4.44
1756
1361
2221
2711
2214
0
151
75
94
165
0
265
278
242
231
OREGO
Адаптивный 4
Гира
DIRK33
DIRK44
RADAU
3.50
1.78
2.36
3.66
3.12
2931
1410
2396
3160
3416
0
236
149
157
200
0
356
317
350
267
4.2. Локально-неустойчивые задачи
Рассмотрим один тип задач, решение которых неявными методами может привести к
качественно неверному результату. Если решение гладкое, то шаг интегрирования
устанавливается большим, но тогда неявные методы подавляют все составляющие
решения, соответствующие большим по модулю собственным значениям якобиана,
независимо от знака действительной части. Поэтому если одно из собственных значений
быстро перемещается в правую полуплоскость и становится очень большим, то неявный
решатель может этого не заметить, и неустойчивый процесс будет моделироваться как
устойчивый.
Рассмотрим задачу
x'
1
= x
2
, x
1
(0) = 2,
x'
2
= μ (1 - x
1
2
) (x
1
+ x
2
), x
2
(0) = 0, 0 ≤ t ≤ 3,
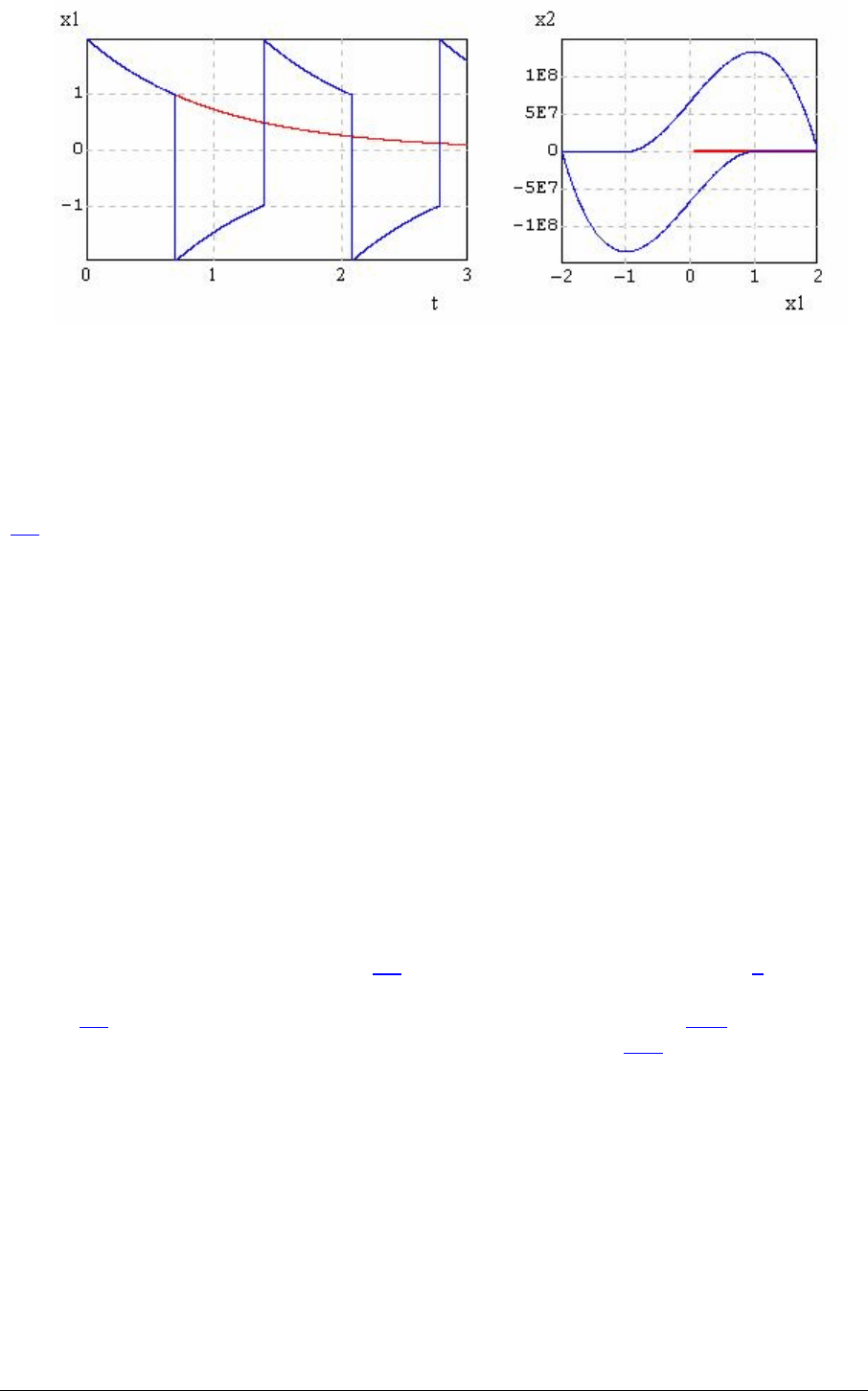
построенную аналогично осциллятору Ван-дер-Поля, но имеющую более резкий переход
от устойчивого состояния к неустойчивому. При больших значениях μ задача является
жесткой. Правильное решение этой задачи при μ = 10
8
показано на рисунке синей линией.
Однако неявные методы обычно дают неправильное решение, показанное на рисунке
красной линией, которое практически не изменяется при изменении задаваемой точности
в широких пределах. Этот факт может привести к ошибочному мнению, что данное
решение является правильным. На приведенном примере видно, что при моделировании
процессов, имеющих быстро нарастающий, катастрофический характер, неявные методы
могут давать совершенно неверный результат, соответствующий устойчивому процессу.
Явные адаптивные методы позволяют качественно правильно решать подобные задачи.
При решении рассмотренной задачи все адаптивные методы давали правильное решение
при умеренных требованиях к точности, при этом лучшими были методы Адаптивный 2,
3, 5.
Решение дифференциальных и дифференциально-алгебраических уравнений в программном комплексе
«МВТУ»
18
5. Решение дифференциально-
алгебраических уравнений (ДАУ)
Часто уравнения математической модели представлены не в нормальной форме Коши
(1.1), а в виде системы ДАУ
(5.1а)
x' = f(x, y), x(t
0
) = x
0
,
(5.1б)
0 = g(x, y), y(t
0
) = y
0
.
Начальные условия x
0
, y
0
называются согласованными, если они удовлетворяют
алгебраическому уравнению. Реализовать уравнения вида (5.1) в ПК «МВТУ» можно с
помощью типового блока F(Y) = 0.
5.1. Метод пространства состояний
Для численного решения уравнений (5.1) можно использовать два способа [6]. Первый из
них (метод пространства состояний) основан на приведении уравнений к нормальной
форме (1.1) путем численного решения алгебраической подсистемы (5.1б) при заданном
векторе x. Подставляя затем полученное значение вектора y в (5.1а), получим искомые
значения производных. Этот способ применяется в ПК «МВТУ» для расчета начального
значения вектора y, а также в процессе интегрирования явными методами. Начальное
значение вектора y можно задать в диалоговом окне блока F(Y) = 0, но если оно не
согласованно, то будет уточнено на этапе инициализации модели. Для решения
алгебраической подсистемы можно использовать один из трех методов: простых
итераций, Ньютона-Рафсона, Бройдена. Метод пространства состояний позволяет
разделить задачи интегрирования ОДУ и решения алгебраических уравнений, поэтому его
можно применять в сочетании с любым методом интегрирования. Но его нельзя
использовать при решении задач высших индексов, когда алгебраическая подсистема
вырождена.
5.2. Метод ε-вложения

Решение дифференциальных и дифференциально-алгебраических уравнений в программном комплексе
«МВТУ»
19
Второй способ (метод ε-вложения) основан на совместном решении дифференциальной и
алгебраической подсистем и может быть интерпретирован как решение сингулярно
возмущенной задачи
x' = f(x, y), x(t
0
) = x
0
,
ε y' = g(x, y), y(t
0
) = y
0
.
при ε = 0. В ПК «МВТУ» этот способ используется в процессе интегрирования неявными
методами. Применяя метод Рунге-Кутты (3.1), получим формулы одного шага
интегрирования системы (5.1) в виде
(5.2а)
;
(5.2б)
,
(5.2в)
.
Формулы (5.2б), (5.2в) задают систему нелинейных алгебраических уравнений
относительно векторов k
i
, l
i
, i = 1, …, s (векторы стадийных значений X
i
, Y
i
, i = 1, …, s
нетрудно исключить). При реализации приведенных формул из уравнений (5.2б), (5.2в)
находим векторы k
i
, l
i
, которые подставляем в (5.2а). Метод ε-вложения позволяет решать
задачи высших индексов, но его можно использовать только в сочетании с неявным
методом интегрирования, поскольку для явных методов система алгебраических
уравнений (5.2б), (5.2в) будет вырожденной.
5.3. Системы ДАУ высших индексов
Согласно определению Гира и др. (см. [6]), индекс дифференцирования системы (5.1) есть
наименьшее число аналитических дифференцирований, требующихся для того, чтобы из
уравнений (5.1) можно было бы получить систему ОДУ в форме Коши. При этом каждое
дифференцирование понижает индекс на 1. Продифференцировав алгебраическую
подсистему (5.1б) и обозначив g
x
= ∂g / ∂x, g
y
= ∂g / ∂y, получим
(5.3)
0 = g
x
x' + g
y
y'.
Если матрица g
y
обратима, то из (5.1), (5.3) можно получить систему в нормальной форме
Коши

Решение дифференциальных и дифференциально-алгебраических уравнений в программном комплексе
«МВТУ»
20
x' = f(x, y), x(t
0
) = x
0
,
y' = -g
y
-1
g
x
f(x, y), y(t
0
) = y
0
.
Итак, если матрица g
y
обратима в любой точки на траектории решения, то система (5.1)
имеет индекс 1, а в противном случае (если матрица g
y
вырождена) индекс системы
больше 1. Системы высших индексов (2 и выше) возникают при решении многих
прикладных задач. Например, уравнения механической системы со связями,
сформированные методом Лагранжа, имеют индекс 3. Такие системы наиболее трудны
для численного решения и могут быть решены только неявными методами.
В качестве примера рассмотрим систему ДАУ
(5.4а)
x' = u, u' = -x z,
y' = v, v' = -1 - y z,
(5.4б)
0 = x
2
+ y
2
- 1,
описывающую колебания маятника. Продифференцировав алгебраическое уравнение
(5.4б), получим
(5.5)
0 = x u + y v,
а продифференцировав (5.5), получим уравнение
(5.6)
0 = -z (x
2
+ y
2
) - y + u
2
+ v
2
из которого можно выразить алгебраическую переменную z через дифференциальные
переменные x, y, u, v. Таким образом, система (5.4а), (5.6) имеет индекс 1, система (5.4а),
(5.5) – индекс 2, а исходная система (5.4) – индекс 3.
Трудность решения систем ДАУ высших индексов обусловлена эффектом, который
получил название «феномен снижения порядка» [6] и заключается в том, что реальный
порядок метода оказывается меньше, чем полученный исходя из классических
представлений. Этот эффект проявляется при решении жестких и дифференциально-
алгебраических систем (особенно заметно – высших индексов). В Приложении приведены
результаты решения уравнений маятника, сформированных в виде систем индексов 1, 2, 3.
Видно, что снижение порядка при увеличении индекса приводит к существенному
увеличению вычислительных затрат, причем только решатель DIRK44 смог решить задачу
индекса 3. Для эффективного решения систем ДАУ высших индексов разрабатывают
специальные методы, удовлетворяющие дополнительным условиям порядка [6]. Среди
решателей ПК «МВТУ» пока нет таких методов, однако решатель DIRK44 позволяет
решать задачи индексов 2 и 3. Для более эффективного решения таких задач нами
разработан метод 4-го порядка с таблицей Бутчера
