Козин В.З. Опробование, контроль и автоматизация обогатительных процессов

Подождите немного. Документ загружается.

>dt

.>d

> d

w(oC)

0,6

0,5

0,4

0,3

0,2

0,1

]v /

' ^^V—-т-^

30 Woc

,%.

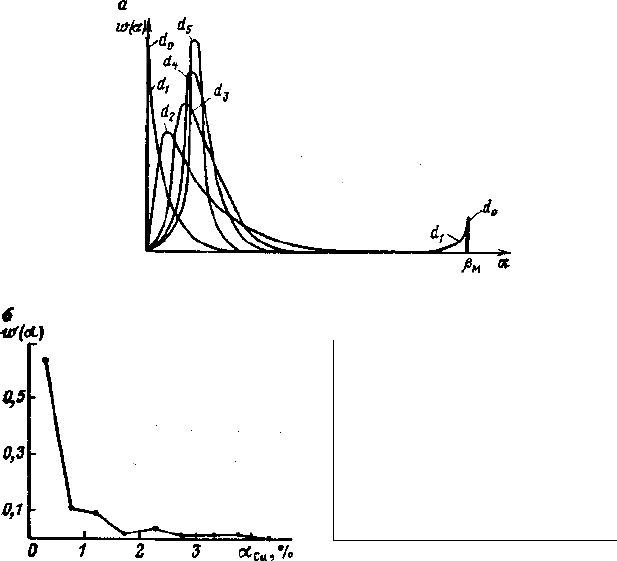
Рис. 2.5. Закономерное изменение распределения массовой доли в отдельных

кусках с изменением их размера

ется не сочетанием кусков минерала и пустой породы, а распре-

делением зерен минерала в исходном горном массиве.

На рис. 2.5, а показана эволюция закона распределения

с увеличением размера кусков. Размер кусков d

соответствует

полностью вскрытым зернам минерала. Размер кусков d\ не-

сколько больше и характеризуется появлением некоторого коли-

чества сростков. Куски размером d^ полностью состоят из срост-

ков и т. д. Куски размером d

столь велики, что различия между

ними по массовой доле компонентов незначительны, а распреде-

ление практически соответствует нормальному закону распре-

деления.

На рис. 2.5, б, в представлены экспериментально полученные

распределения массовой доли меди и серы в кусках медной

руды, соответствующие приблизительно кускам размеров d

и d

(см. рис. 2.5, а).

Третья закономерность — распределение массовой доли ком-

понентов в отдельных кусках закономерно изменяется от дис-

кретного (размер кусков do) до нормального (размер кус-

ков d

Обобщая, сформулируем основную закономерность распре-

деления массовой доли в точечных пробах; распределение мас-

совой доли определяемого компонента в точечных пробах (от-

дельных кусках) w(a) является функцией массы точечных проб

(кусков) q

, а также массовой доли определяемого компонента

а, в общем случае асимметрично w(a) =f(q

, а).

§ 2.5. ДИСПЕРСИЯ ПОКУСКОВОГО ОПРОБОВАНИЯ

Кусок — естественный элемент неоднородности опробуемой

массы. Закономерное изменение распределения с изменением

размера кусков приводит к закономерному изменению основной

характеристики распределения — дисперсии. Назовем такую

дисперсию дисперсией покускового опробования. Близкий ана-

лог этого понятия — контрастность руды. В соответствии с из-

менением распределения дисперсия покускового опробования s

будет изменяться от максимального значения s

max при малых

размерах кусков до нуля для очень больших кусков. Типичный

вид зависимости дисперсии покускового опробования от раз-

мера кусков s

(d) представлен на рис. 2.6.

Эта зависимость может иметь некоторый горизонтальный

участок АВ, размер которого зависит от размеров зерен мине-

рала, содержащего определяемый компонент.

Эту величину можно оценить по формуле Годэна для вкрап-

ленных руд

РР = [(4—d

)/d

]

где р

— доля раскрытого минерала.

Приблизительно можно считать, что эта зона составляет

(0-г-0,1) d

, где d

— характерный размер зерна.

Распределение массовой доли компонента в этой зоне при

покусковом опробовании описывается дискретным законом, по-

этому диапазон АВ зависимости s

(d) назовем зоной дискрет-

ного закона. В этой зоне дисперсия покускового опробования

максимальна и не зависит от размера кусков.

Для зоны дискретного закона s

дз = 5

max = const. Даль-

нейший ход зависимости s

(d) (участок BCD) предопределя-

ется структурой кусков, т. е. тем, каким образом будут зерна

группироваться в отдельных кусках, равномерно распределяясь

в рудной массе, либо образовывая скопления, составляющие

в итоге некоторые пространственные фигуры (жилы, слои). Ха-

рактер группировки будем в дальнейшем описывать показате-

лем Ь. Следовательно, в переходной зоне (участок BCD) дис-

персия покускового опробования является не только функцией

-s

(d,d

,b)

4-4

(d)

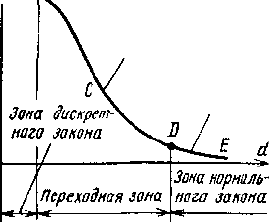
Рис. 2.6. Типичный вид зависимости

дисперсии покускового опробования

от размера кусков

размера куска d, но и размера зерна d

и характера группи-

ровки Ь

si.

si (d, d

, b).

Для кусков большого размера влияние характера группи-

ровки зерен на массовую долю компонента в куске становится

слабым по сравнению с влиянием макронеоднородностей руд-

ного тела. Если эти макронеоднородности не закономерны, то

отличия одних больших кусков от других предопределяются слу-

чайными отклонениями, а распределение массовой доли компо-

нента в таких кусках приближается к нормальному. Поэтому

дальнейшее изменение дисперсии покускового опробования

(участок DE) зависит только от размера этих кусков, т. е. в зоне

нормального закона

к. знз

(d).

Зависимость s

(d) можно найти экспериментально. С этой

цельдо из пробы следует выделить некоторое число узких клас-

сов. В каждом классе отобрать около 100 кусков и для каждого

куска определить массовую долю компонента ai(d), после чего

определяются точки кривой (см. рис. 2.6) по формуле

n(d)

&(d)=L, Wi(d) — a]

/[n(d)—l],

t=i

(2.15)

где n(d) — число отобранных кусков в классе с размером кус-

ков d; ai(d) — массовая доля определяемого компонента в t'-м

куске этого класса; а — средняя массовая доля в пробе.

Для кусков малого размера анализ отдельных кусков может

быть невыполним. Тогда следует для анализа готовить каждый

раз вместо одного сразу т кусков с последующим пересчетом

дисперсии

si (d) = mslt (d),

где s

(d) — дисперсия, определенная по формуле (2.15) при

анализе навески, подготовленной из т небольших кусков. За-

висимость дисперсии покускового опробования от размера кус-

ков — фундаментальная характеристика опробуемой массы и,

в отличие от распределения массовой доли в точечных пробах,

является неизменной. Найденная однажды для опробуемой

массы s

(d) может быть использована в любых последующих

расчетах. Как объективная и неизменная характеристика опро-

буемого массива эта закономерность фундаментальна и на ее

основе формулируются все основные законы опробования.

§ 2.6. МАКСИМАЛЬНАЯ ДИСПЕРСИЯ

ПОКУСКОВОГО ОПРОБОВАНИЯ

Величину s

max в зоне дискретного закона можно определить

аналитически по формуле [11]

si max = (рм/рп) « (Рм — «) [1 — а/р

+ Оф

/(рмРм)]

. (2.16)

Для малых а< (0,05^-0,1) р

из формулы (2.16):

4 max = (Рм/рп) «Рм, (2.17)

где р

, р

— плотность соответственно минерала и породы; а,

— массовая доля определяемого компонента соответственно

в опробуемой массе и в минерале.

Формулу (2.16) удобно записать в относительном виде

si max/Рм = (Рм/рп) (а/р

) (1 — а/р

) [1 —а/рм + (Рп/рм) (а/рм)]

Такую функцию можно представить графически (рис. 2.7) для

разных рм/рп-

Примеры использования формул (2.16), (2.17) и рис. 2.7.1. Для мед-

ного концентрата а=18%; (З

=34,5 %; р

=4,2 г/см

; р

=2,8 г/см

. Отно-

сительные значения а/(З

= 18/34,5=0,52 и рм/рп=1,5. По рис. 2.7 находим

K тах/Р

м = 0,27. Следовательно, максимальная дисперсия покускового опро-

бования для медного концентрата s

max=0,27pV=321,36 (%)

2. Для медных хвостов а=0,05 %; р

=34,5 %; Рм = 4,2 г/см

и р

= 2,8 г/см

. Удобнее воспользоваться формулой (2.17) s

max ==(4,2/2,8) X

Х0,05-34,5 = 2,59 (%)

3. Для золотой руды а=2 г/т; р

=10

г/т; р

=18 г/см

; р

= 2,8 г/см

Следовательно, s*

max = (18/2,8) • 2 • 10

= 12,86 • 10

(г/т)

4. Для угля зольностью 20 % (а=20 %), зольностью породы 100 %

(рм = Ю0%), плотностью породы 2 г/см

и плотностью угля 1,4 г/см

по

формуле (2.16) имеем s^

max

= (2/1,4) • 20- (100—20)[1—20/100+20Х

X 1,4/(100-2)]

= 2019,66 (%)

В последнем примере следует обратить внимание на понятие «определяе-

мый компонент». Характеристикой качества угля является зольность. Опре-

О 0,1 0,2 0,3 0,4- 0,5 0,6 0,7 0,8 0.9 cX.'/fi

Рис. 2.7. Зависимость дисперсии покускового опробования от массовой доли

(обе величины нормированы по массовой доле компонента в минерале):

1—6 — соответственно при Р

/Р

. равном 1; 2; 3; 4; 5; 6

деляемый в этом случае минерал (порода) имеет массовую долю определяе-

мого минерала В

=100 % и плотность его 2 г/см

Если бы расчет вести по горючей массе, то, приняв плотность горючей

массы 1,3 г/см

и массовую долю горючего в угле 96 %, имеем s

mai =

= (1,3/1,4) -80- (96—80)[1—80/96+80- 1,4/(96-1,3)]

= 1345,84 (%)

Максимальная дисперсия покускового опробования соответ-

ствует полностью вскрытым зернам полезного минерала, причем

таким образом, что сростки отсутствуют. Строго говоря, это воз-

можно лишь при d-+-0. Однако для многих видов продуктов с до-

пустимой мерой приближения такое состояние можно полагать

и при кусках значительно большего размера (например, россып-

ное золото, уголь, калийные соли, асбест и т. п.). Такое состоя-

ние продукта будет описываться при покусковом опробовании

только дискретным законом, а диапазон изменения дисперсии

покускового опробования АВ (называемый зоной дискретного

закона) описывается максимальной дисперсией, не зависящей

от размера куска.

§ 2.7. ВЕРОЯТНАЯ СИСТЕМАТИЧЕСКАЯ ПОГРЕШНОСТЬ

И УРАГАННЫЕ ПРОБЫ

Асимметричность распределения массовой доли компонентов

в продуктах обогащения проявляется специфическим образом

в том, что вероятность отклонений разного знака от среднего

различна. Это значит, что для руды и хвостов чаще наблюдают

малые отрицательные отклонения и реже — большие положи-

тельные. Среднее арифметическое в этих условиях является

Рис. 2.8. К определению понятия ве-

роятной систематической погрешности

Mcfctpt

вполне определенным лишь при бесконечном увеличении числа

наблюдений (кусков, проб, измерений). Реально никогда не

имеется бесконечное число наблюдений, чаще не располагают

даже достаточно большим их набором. Влияние конечного и,

как правило, малого числа наблюдаемых единиц информации

при опробовании проявляется в том, что результаты группиру-

ются не вокруг среднего, а возле некоторого смещенного от сред-

него значения, меньшего для правоасимметричных распределе-

ний и большего — для левоасимметричных. Следовательно, при

малом числе наблюдений вероятнее будет наблюдаться мода

Мо(а), а не среднее а, т. е. определяя среднее при асимметрич-

ном распределении по малому числу проб, вероятнее всего будет

допущена систематическая погрешность

Да = Мо(сс) — а. (2.18)

Назовем эту погрешность вероятной систематической Да

ве

(рис. 2.8).

Для основных типов асимметричных аппроксимирующих

распределений вероятная систематическая погрешность:

для ^-распределения (если оно имеет вершину)

-a

min

)/(a+ b—2) — (a—a

mln

/ЛОСвер

a, b

(a—l)(a,

где а, о — параметры распределения. Если р-распределение

имеет вид убывающей функции, то Аа

ве

р =—а, а если имеет вид

возрастающей функции и при a

in = 0, то Да

ве

р = <Хтах—a;

для ^-распределения (правосторонняя асимметрия)

JVa

-s

/(/Va),

при

Да

вер

(2.19)

при /Va

Давер = — а;

для логарифмически-нормального закона распределения

Да

вер

= ехр [In а—0,5 In (1 + Sa/ot

)] — a.

Асимметрия плотностей распределения массовой доли опре-

деляемого компонента в точечных пробах при ограниченном

числе точечных проб приводит к смещенной оценке средней

массовой доли.

Пример. Средняя массовая доля равна 0,141%, мода — 0,0942%.

Следовательно, вероятная систематическая погрешность по формуле (2.18)

для отдельного часового измерения составит

Да

вер

= 0,0942 — 0,141 = — 0,0468 %,

что соответствует относительному занижению массовой доли в хвостах на

33 %. При использовании в расчетах среднего значения а=0,141 %, найден-

ного по 240 измерениям, вероятная систематическая погрешность составит

по формуле (2.19), если s

=0,0808,

Ла

вер

= — (0,0808)

/(240-0,141) = — 0,00019 %.

Это соответствует относительному занижению массовой доли в хвостах всего

на 0,13%.

Следует помнить о сути вероятной систематической погреш-

ности. Точно так же, как дисперсия характеризует случайную

погрешность, но не позволяет предсказать ее в каждом отдель-

ном опыте, так и вероятная систематическая погрешность, ха-

рактеризуя наиболее вероятные отклонения наблюдаемого по N

пробам результата от среднего для бесконечного числа наблю-

дений, не дает оснований утверждать, что именно такое откло-

нение будет в каком-либо конкретном наблюдении.

Понятие вероятной систематической погрешности позволяет

объяснить ряд наблюдаемых при опробовании эффектов, пред-

сказать новые и указать недостатки некоторых распространен-

ных приемов отбора и подготовки проб.

§ 2.8. МИНИМАЛЬНАЯ МАССА ПРОБЫ

Различные куски опробуемого массива имеют различную мас-

совую долю определяемого компонента. Это различие характе-

ризуется дисперсией покускового опробования s

. Если задана

допустимая погрешность отбора пробы s

aon

, то при случайном

отборе отдельных кусков от всего опробуемого массива обес-

печить ее может только отбор в пробу некоторого числа кусков

п. Это число можно найти из формулы, связывающей дисперсию

среднего значения массовой доли а с дисперсией покускового

опробования. Приняв s-=-s

Aon

, получим

Следовательно, для обеспечения s

flon

в пробу нужно ото-

брать п кусков:

2 / 1

п — S

/Sflorr

Для опробуемого массива, состоящего из кусков одинако-

вого размера d массой <7к=р^

, получим формулу минимальной

массы пробы

q=(sl/slon)pd*. (2.20)

Формула (2.20) является основной формулой минимальной

массы.

Если р измеряется в г/см

, d в мм, a q в кг, то нужно ввести

согласующий множитель 10~

</=10-

/sJon)pd

. (2.21)

Размерности s

и s

AOn

в формуле (2.21) могут быть лю-

быми, но обязательно одинаковыми.

Переход к опробуемым массам, содержащим куски различ-

ного размера, выполним с помощью распределения кусков по

крупности w(d)

max r, о

<7= f [sl(d)/sl

}pd*w{d)dd. (2.22)

Так как дисперсия покускового опробования зависит от раз-

мера кусков, в формуле (2.22) введена функция s

(d).

Для равномерного закона распределения крупности w(d) —

= 1/dmax, ПрИНЯВ d

max

=2d И S

(d), ПОЛуЧИМ

q = 2[sl(d)/sl

]pd*. (2.23)

Если d определяется с помощью ситового анализа, то вводят

коэффициент формы f

<7 = 2[4(d)/&„]/pg. (2.24)

В последующем индекс с при величине d можно опускать,

имея в виду, что при практических расчетах для согласования

определяемых с помощью ситового анализа размеров кусков

с истинными в формулы вида (2.23) следует вводить коэффи-

циент формы f.

С учетом указанных выше размерностей формула (2.24),

как основная рабочая формула минимальной массы, примет

вид:

q = 2-10-* [si (dyslojfpd*. (2.25)

Итак, минимальная масса пробы по формуле (2.25) является

в общем случае функцией куба размера кусков опробуемой

массы

q = k(d)~d

, (2.26)

где

k (d) = 2 • 10-« [si (d)/sl

] /p. (2.27)

В формулы (2.26) и (2.27)_ входит одна экспериментально

определяемая величина s

(d). Остальные либо задаются

(£

доп, f, d)

либо определяются общепринятым образом (р).

В формулу минимальной массы входит дисперсия поиско-

вого опробования s

(d), которая тоже зависит от размера

кусков. Это двойное влияние размера кусков приводит к изме-

нению общей степени при размере кусков в формуле минималь-

ной массы. Сама же минимальная масса пробы сложным обра-

зом зависит от размера кусков.

В соответствии с выделенными зонами изменения дисперсии

покускового опробования, получим соответствующие формулы

минимальной массы пробы.

В общем случае дисперсия покускового опробования зависит

от размера куска, размера зерна и характера вкрапленности.

В зоне дискретного закона любой продукт вскрыт, поэтому

дисперсия покускового опробования максимальна и постоянна

[см. формулы (2.16), (2.17)], а минимальная масса однозначно

предопределяется кубом размера кусков

g-2[s

Kmax

/sJ

n]/pd

. (2.28)

В переходной зоне дисперсия покускового опробования за-

висит от размера кусков, размера вкраплений и характера

вкрапленности. Подставив выражение для s

(d) [11] в общую

интегральную формулу (2.22) и взяв интеграл, получим

q = [8/(4-6) (6 + 1)] (a$Jsl

udl-

. (2.29)

В работе [11] показано, что 6 = 0 для редкой равномерной

вкрапленности минерала; 6=1 для жильной вкрапленности; 6 =

= 1,5 для неравномерной вкрапленности; 6 = 2 для слоистой

вкрапленности; 6 = 3 для случая, когда куски представлены либо

чистым минералом, либо породой.

Минимальная масса в переходной зоне в зависимости от ха-

рактера вкрапленности, описываемого показателем 6, по-раз-

ному зависит от размера кусков. Показатель степени при d

может изменяться от 0 до 3.

Важно заметить, что суммарный показатель степени при

размере кусков и размере зерен вкраплений всегда равен трем.

Формула (2.29) справедлива для бедных продуктов (а<

<0,1 р

). Для богатых продуктов нужно использовать общие

формулы дисперсии покускового опробования (2.16) и мини-

мальной массы (2.22).

В зоне нормального закона минимальная масса не зависит

от крупности

q = 2[sl.Jsl

]^dl, (2.30)

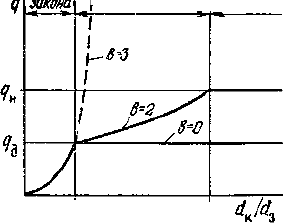
Рис. 2.9. Закономерное изменение ми-

нимальной массы пробы с изменением

размеров кусков опробуемого массива

для кусков различной структуры

(различное значение показателя Ь)

Зона, дис-

кретного

Переходная Зона нормаль-

зона \ного закона

где d

— любой размер кусков для зоны нормального закона,

для которых экспериментально определена дисперсия покуско-

вого опробования s

На рис. 2.9 приведены зависимости, построенные по форму-

лам (2.28) — (2.30) для трех зон. Видно, что минимальная масса

пробы сложным образом зависит от размера кусков опробуемой

массы. Начальный участок этой зависимости всегда представ-

ляет собой кубическую параболу. Эта закономерность для всех

вскрытых продуктов (6 = 3) сохраняется и в дальнейшем. Для

продуктов, содержащих сростки, эта зависимость в переходной

зоне тем больше отклоняется от кубической параболы, чем

меньше 6. Для 6=0 минимальная масса в переходной зоне не

зависит от размера кусков опробуемой массы. В зоне нормаль-

ного закона эта зависимость также отсутствует, однако мини-

мальная масса зависит от достигнутого ею уровня к концу пе-

реходной зоны.

Выделенные участки на рис. 2.9 для реальных условий будут

иметь сглаженные переходы один в другой.

Широко распространенные простые формулы минимальной

массы

Kd*

или

(2.31)

(2.32)

являются эмпирическими, так как коэффициент К в формуле

(2.31) и К и а в формуле (2.32) определяются только экспери-

ментально, а показатель степени постоянный (2), либо пере-

менный (а) соответствуют, как правило, узкому диапазону из-

менения крупности. Недостаток формул (2.31) и (2.32) —скры-

тое использование допустимой погрешности, в результате чего

обычно неясны условия экспериментального определения К и а,

а также какова погрешность их использования.

Гораздо определеннее использовать общую формулу (2.26).

Видно, что коэффициент K(d) может изменяться в гораздо

более широких пределах, и по формуле (2.27) он вполне естест-

венно предопределяется свойствами руды (s

(d), p, f) и допус-

тимой погрешностью fs

AOn

В табл. 2.1 приведены основные формулы, записанные для

d = const, интегральные, записанные с учетом распределения па-

раметров кусков w(d) и зерен w(d

) и рабочие — полученные

из интегральных при некоторых условиях, указанных

в табл. 2.1.

Пример. Найти минимальную массу пробы при опробовании золото-

носного песка, состоящего из чистых золотинок и песчинок одного размера.

Ожидаемая массовая доля золота а=2 г/т (р

=Ю

г/т), плотность мине-

рала р

=18 г/см

, плотность породы 3 г/см

, d

max = l мм, распределение

w(d)—равномерное, / = 0,5.

Решение. Для зоны дискретного закона для s

n = 0,05 г/т q = 2- 10~

X/pfi?c

|sK

(rfc)/s

on] = 2-10-

-0,5.3-0,5

[12-10

/0,05

]==1800 кг. Здесь s

= (рм/р)а|3м==12-10

(г/т)

. Для s

„

n=0,4 г/т q=2 • 10"

• 0,5 • 3 • 0,5

[12Х

Х10

/0,4

]=28,125 кг.

В основной рабочей формуле (2.25) минимальной массы

пробы неизвестной является дисперсия покускового опробова-

ния s

). Для ее определения необходимо отобрать 50—100

кусочков опробуемого материала размером приблизительно d

Отбор следует выполнять, равномерно распределив кусочки по

всему опробуемому массиву. Можно также отобрать каким-

либо общепринятым способом пробу, соответствующую опробуе-

мому массиву, выделить рассевом узкий класс, близкий к d

, и

отобрать от него сокращением 50—100 кусочков, для каждого

из которых следует выполнить анализ массовой доли опреде-

ляемого компонента. После этого s

) определяется по из-

вестной формуле дисперсии.

Широкое распространение получили упрощенные формулы

(2.32), которые для конкретных условий могут быть получены

экспериментально, что и отражают все существующие в на-

стоящее время ГОСТы. Так как ГОСТы разрабатываются на ос-

нове экспериментальных работ, в указанных ГОСТами усло-

виях эти формулы пригодны для использования. Недостатком

является отсутствие указаний о сопутствующих этим формулам

погрешностях. Неправильно также стремление расширить об-

ласть использования таких формул.

Экспериментальная основа определения коэффициентов К и

a — широко известная методика П. Л. Каллистова, которая со-

стоит в определении минимальных масс q\ и q^ для двух клас-

сов крупности опробуемого материала d

и d

, после чего реше-

нием системы двух уравнений находят неизвестные коэффици-

енты К и а

<7imi

-K^i;

^2min = ^2

Минимальные массы q\

min и с/2 min определяют следующим

образом (рис. 2.10, а). Пробу крупностью d\ и массой Q

заве-

домо большей, чем предполагаемая минимальная масса, сокра-

щают пополам. Одну половину делят на 16 порций массой q

измельчают их без сокращения до крупности 0,1 мм и сдают на

химический анализ. По 16 результатам анализа вычисляют

среднюю квадратическую погрешность s

вторую половину

вновь делят пополам и из четверти исходной массы сокраще-

нием формируют 16 проб массой q

(<72 = 0,5 #i)> вычисляют s

и т. д. В итоге можно для некоторой серии масс q\, q

,.. ., qi

построить зависимость s

от массы проб q. Характерный вид

Сокращение пополам

Деление на 16 частей

I. \

Сокращение пополам

Деление на 16 частей

t Сокращение пополам

Целение' на 16 частей

Сокращение пополам

Деление на 16 частей

f ~1

и т.д.

min

Ь min

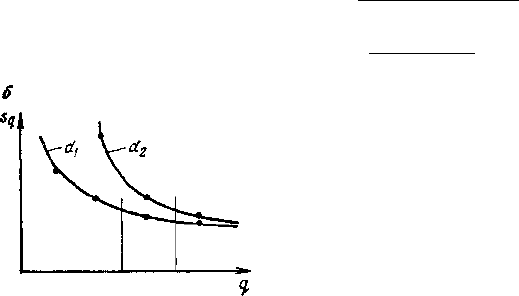
Рис. 2.10. К определению ми-

нимальной массы по методике

П. Л. Каллистова:

а — схема опытов; б — теоретиче-

ское изменение дисперсии массо-

вой доли в параллельных частях

такой зависимости приведен на рис. 2.10, б для пробы круп-

ностью d\. Аналогично проводят работу с другой пробой круп-

ностью d

и массой Q

, построив зависимость погрешности от

массы для крупности d

. Минимальную массу пробы устанавли-

вают по графику, считая, что масса, при которой погрешность

перестает существенно снижаться, и есть минимальная для дан-

ной крупности (например, q\

m и q

2mm

на рис. 2.10, б).

§ 2.9. ЧИСЛО ТОЧЕЧНЫХ ПРОБ

ПРИ СЛУЧАЙНОМ ИЗМЕНЕНИИ СВОЙСТВ МАССИВА

Основная характеристика случайного изменения свойств мас-

сива — дисперсия массовой доли в точечных пробах s

Погрешность объединенной пробы, составленной из N точеч-

ных проб, определяют по формуле

а т

Допустимую для отбора погрешность 5

Д0П

обеспечивает число

точечных проб N = s

aon

. Из этой формулы следует известная

формула N=K

T. Здесь К—квантиль распределения, со-

ответствующего точечным пробам. Обычно считают /С=2; V —

коэффициент вариации точечных проб; Р

от

— допустимая отно-

сительная погрешность отбора проб. V и Р

0Т

следует принимать

одинаковой размерности (проценты или доли единицы).

Стандартизованные способы определения числа точечных

проб. Определение дисперсии точечных проб эксперименталь-

ным путем представляет трудоемкую задачу. Поэтому при раз-

работке нормативных документов (ГОСТов, ОСТов) изучают те

виды массивов, для которых разрабатывают рекомендации, на-

ходят диапазоны изменения характеристик этих массивов и ре-

комендуют рассчитывать N без экспериментального определе-

ния дисперсии точечных проб. При этом число точечных проб

обычно связывают с массой опробуемого массива, которая ори-

ентировочно (а иногда и точно) известна.

В основе использования массы как показателя неоднородно-

сти лежит интуитивное соображение о том, что, чем больше

масса, тем труднее ее перемешать и тем неоднороднее она

должна быть. Следовательно, чем больше опробуемая масса,

тем больше точечных проб следует от нее отобрать. Кроме того,

чем больше опробуемая масса, тем ответственнее опробование

и тем точнее результат стремятся получить.

В итоге формируют формулы или таблицы, включающие

обычно опробуемую массу и в определенной мере массу точеч-

ной пробы, проявляющуюся отчасти в коэффициенте вариации

V точечных проб для опробуемого массива.

Так, ГОСТ 14180—80 на руды и концентраты цветных метал-

лов узаконил формулу

N = 0,075V УМ,

где V — коэффициент вариации, %; М— масса, т.

ГОСТы 15054—80 и 16598—80 задают погрешность отбора

пробы на железо и марганец как функцию массы.

Рекомендуемые этими ГОСТами погрешности отбора проб

•(%) приведены ниже:

ГОСТ 15054—80 16598—80

Масса партии, тыс. т:

до 0,5 0,90 0,70

свыше 0,5 до 1 .... 0,78 0,55

1—2 0,70 0,46

2—5 0,59 0,42

5—15 0,49 0,39

15—30 0,45 0,37

30—45 0,42 0,35

45—70 0,40 —

70—100 0,37 —

Число точечных проб, таким образом, определяется как

•функция массы.

Особенность железных и марганцевых руд позволяет регла-

ментировать средние квадратические отклонения массовой доли

железа (марганца): малая вариация s

=l,25 % (0,75 %), сред-

няя—1,75 % (1,75 %), большая —2,5 % (2,25 %).

Согласно ГОСТ 10742—71, для обогащенного каменного угля

"и антрацита число точечных проб для партии массой до 1000 т

всегда равно 16, а для массы свыше 1000 т определяется по

формуле

ы = тл/Мпт, •

где М — масса партии, т.

Для необогащенного каменного угля и антрацита для пар-

тии массой до 1000 т N всегда равно 32, а для больших масс

N = 32 УМ/1000.

При этом ГОСТ 10742—71 регламентирует и массу точечной

пробы q

(кг):

>0,06d

ax,

где

maK

принимается в миллиметрах.

Там же указаны и базовые погрешности опробования: отно-

сительная ±10 % Для зольности до 20 % и абсолютная ±2 %

для зольности более 20 % •

Примеры. 1. Определить число точечных проб по ГОСТ 14180—80 для:

партии свинцового концентрата массой Л1=700 т, коэффициент вариации то-

чечных проб 19 %

N = 0,075-19 л/700 = 38.

2. Определить число точечных проб по ГОСТ 15054—80 при опробова-

нии железного концентрата массой 3000 т с большой вариацией среднего

квадратического отклонения массовой доли

ЛГ = 4-2,5

/0,59

= 72.

§ 2.10. ЗАВИСИМОСТЬ МИНИМАЛЬНОЙ МАССЫ

ОБЪЕДИНЕННОЙ ПРОБЫ ОТ МАССЫ ТОЧЕЧНОЙ ПРОБЫ

Полную дисперсию массовой доли компонентов s

в опробуе-

мом массиве условно можно представить как сумму дисперсии

средних массовых долей в некоторых локально ограниченных

массах s

и дисперсию массовых долей в отдельных кусках

этих масс s

. cp

2 2 , 2

Sa — S

p -p- S

p •

Используя правило для дисперсии среднего, получим, что'

дисперсия погрешности оценки массовой доли объединенной

пробы будет равна

sl = s

JN + s

/(Nn

), (2.33)

где N — число точечных проб или, другими словами, число уч-

тенных в объединенной пробе локально ограниченных масси-

вов; п

— число кусков в точечной пробе.

Из формулы (2.33) следует известное правило: число точеч-

ных проб (N) увеличивать всегда выгоднее, чем массу точечных

проб (п

). Для неоднородного массива это приводит к сильному

возрастанию минимальной массы неоднородного массива

(йн. и) с увеличением массы точечных проб: q

= ^ + ^

{п

—

— 1) s

p/s

ROTi

. Здесь q—минимальная масса для однородного

массива, найденная по формулам (2.25), (2.29), (2.30); q

—

масса кусков; s

aon

— допустимая средняя квадратичная погреш-

ность для отбора пробы. Из приведенной формулы видно, что

наименьшая минимальная масса будет при п

=\, т. е. при от-

боре проб в точечную пробу одного куска (покусковой отбор-

проб).

§ 2.11. ОПТИМАЛЬНЫЙ ПРОБООТБОР

Из условия, что наименьшая минимальная масса возможна

лишь при покусковом отборе точечных проб, следует, что спо-

собы отбора проб неравнозначны и покусковой отбор точечных

проб предпочтительнее других вариантов. Если этот отбор од-

повременно обеспечивает получение начальной массы пробы q

равной необходимой д

, то получим оптимальный пробоотбор.

Оптимальный пробоотбор — покусковой отбор точечных

проб, обеспечивающий равенство

= q» = q. (2-34)

Число точечных проб при оптимальном пробоотборе равно

числу кусков в объединенной пробе

N = q

, (2.35)

где q

— масса отбираемого куска.

Число точечных проб, обеспечивающих минимальную массу

пробы,

N=sl(q«)/sl

. (2.36)

Из равенств (2.34) —(2.36) следует уравнение оптимального

пробоотбора

= si (q

)/sl

n. (2.37)

Уравнение (2.37) оптимального пробоотбора можно запи-

сать в следующем виде:

2 / v 2

<7к$к \Як) — 9д5доп-

Величины <7д и s

flon

являются заданными.

Дисперсия покускового опробования s

является функцией

размера, а значит и массы куска q

(см. рис. 2.6), т. е. s

Из уравнения ^

) =^s

on можно найти массу куска

^к. опт, удовлетворяющую требованию оптимального пробоот-

бора. Это значит, что отбирая в точечные пробы по одному

куску массой q

. опт, в итоге получим необходимую массу, рав-

ную минимальной.

При этом будет отобрано ЛГ

опт

точечных проб-кусков

А^опт = SK (q

. оптУядоп- (2.38)

Если, например, дисперсия s

) не зависит от q

, а это со-

ответствует всем вскрытым материалам, т. е. продуктам, состоя-

щим из чистых кусков породы и минералов, при этом s

= s

max, то масса точечных проб-кусков

чк. опт —

onlSK max (2.39)

И ИХ ЧИСЛО

Л/опт = SK тах/Ядоп. (

)

Формулы (2.39) и (2.40) следуют из выражений (2.37) и

(2.38).

Рис. 2.11. К решению уравнения оп- щ-Зу

тимального пробоотбора

" 0 0,010,013 Ш ЦВЗ^кг

Естественно, что точечные пробы-куски должны быть отоб-

раны от всего массива, т. е. соответствующим образом распре-

делены в нем.

Пример. Экспериментальным путем для медной руды с массовой до-

лей о=1 % получена зависимость s

Наносим ее на график (рис. 2.11, линия /). Умножаем точки линии

) на величину q

и проводим линию 2. Вычисляем величину г/=<7д5

ДО

п.

Необходимо отобрать пробу массой 2 кг с относительной погрешностью 5 %.

Тогда 5

оп=5-1/(2-100) =0,025%; г/=<7д5

доп=2-0,025

=1,25-10"

(кг-%

Проводим горизонтальную линию 3 с t/=l,25-Ю

-3

. Точка ее пересече-

ния с линией <7KS

(<7K) Даст значение оптимальной массы куска q

. опт =

=0,013 кг. Соответствующее этому q

значение SK

(<7K)=0,1 (%)

. Число

точечных проб-кусков составит #опт = 0,1/0,025

=160.

§ 2.12. ТРИ ВАРИАНТА РАСЧЕТА ПАРАМЕТРОВ

ОТБОРА ПРОБ

При решении задач отбора проб возможны различные вари-

анты сочетаний исходных данных и, соответственно, различ-

ными будут и расчетные показатели.

Обычно вначале выбирают способ и технику отбора проб,

что предопределяет массу точечной пробы q

, которую рассчи-

тывают для принятого оборудования (например пробоотбирате-

лей) по известным формулам. Всегда должна быть задана

также допустимая погрешность отбора объединенной пробы

Д0П

. В этом случае экспериментально определяемая характери-

стика опробуемого массива — дисперсия точечных проб s

После экспериментальной оценки s

выполняется расчет

числа точечных проб

/V = Sj/S^ou'

Начальная масса пробы q

, равная в этом случае минимальной

q, равна q

= q

N=q.

В этом первом варианте расчета обеспечивается равенство

минимальной и начальной масс, но не учитывается необходимая

масса пробы, которая может оказаться как больше, так и

меньше начальной.

Если необходимая масса больше полученной начальной, то

может быть произвольно увеличено число точечных проб N на-

столько, чтобы начальная масса пробы стала равной необходи-

мой. Погрешность результата опробования s

pe3

окажется при

этом меньше допустимой при отборе Ядоп.

Если необходимая масса будет меньше полученной началь-

ной, то в последующем пробу придется сокращать, и погреш-

ность результата s

3, возрастает по сравнению с использован-

ной допустимой погрешностью отбора s

Hon

Этот вариант расчета общепринят, так как варьируемой ве-

личиной оказывается число точечных проб, которым легко уп-

равлять. В той или иной форме этот вариант используют госу-

дарственные стандарты.

Менее распространен второй вариант, при котором заданы

число точечных проб N и допустимая погрешность отбора объ-

единенной пробы Ядоп- В этом случае экспериментально опреде-

ляемыми характеристиками опробуемого массива являются

средняя масса кусков q

и дисперсия массовой доли в таких кус-

ках s

. Следует также определить дисперсию точечных проб

некоторой, заведомо большой массы q

=fpd

& = 2 («к i — а

)

/(п

— 1);

i=\

N _

=£ (oL

— OL^fl{N — 1) ИЛИ S? =

= 0,25 Да

= 0,25 (a

max

—a

mIn

Здесь f — коэффициент нормы; р — плотность руды; d

— раз-

мер ячейки сита, на котором остается 50 % пробы по массе;

£ — массовая доля определяемого компонента в £-м куске;

« — массовая доля в £-й точечной пробе; п

, N — число ото-

бранных для определения s

либо s

кусков, либо точечных

проб; a

ax, amin — соответственно максимальная и минималь-

ная массовая доля на расчетном контрольном периоде.

Используя основное уравнение погрешностей объединенной

пробы s^ = (s

-{-sVn

)lN, определяем минимальную массу

пробы q, равную начальной q

q = q

J{ Nslon — 4) = <7к

и массу точечной пробы

= qJN.

Заданные величины N и s

Aon

должны быть такими, чтобы

соблюдалось неравенство A^s

fl0

n>s

, т. е. знаменатель в фор-

муле для q должен быть положительным.

Во втором варианте расчета также обеспечивается равен-

ство минимальной и начальной масс, но не учитывается необхо-

димая масса пробы q

. Если необходимая масса больше полу-

ченной начальной, то следует увеличить массу точечных проб до

qJN.

При этом будет достигнута погрешность результата s

pe3

не-

сколько меньше допустимой погрешности отбора s

fl0n

Если необходимая масса меньше полученной q

, то в после-

дующем пробу придется сократить, и погрешность результата

pe3

возрастет по сравнению с s

fl0n

Второй вариант расчета реализуем, если есть возможность

менять массу точечной пробы.

Третий вариант расчета — реализация оптимального пробо-

отбора, при котором обеспечивается равенство трех масс: необ-

ходимой, начальной и минимальной: q

= q

= q. Заданной в этом

случае является именно необходимая масса q

. Равенство ее ос-

тальным обеспечивается выбором куска, составляющего соб-

ственно точечную пробу, и числа точечных проб-кусков.

Экспериментально определяемой в этом случае является за-

висимость дисперсии массовой доли определяемого компонента

в отдельных кусках от их массы. Для этого некоторая проба

должна быть рассеяна на классы крупности и для каждого-

класса найдена дисперсия массовой доли в кусках

si (qj) = Z (

к а —«к/)

/("к /— 1),

где а

ц — массовая доля компонента в £-м куске /-го класса-

крупности. В итоге может быть получена зависимость s

)

дисперсии массовой доли компонента в кусках от их массы до-

определяем оптимальную массу куска, решая уравнение оп-

тимального пробоотбора

2 / \ 2

</к$к (Як) — <7д5доп-

В зависимости от вида функции s

), где неизвестной вели-

чиной является масса куска q

, это уравнение может быть ре-

шено аналитически, либо одним из машинных методов на ЭВМ.

Определяем число кусков — точечных проб

N=q

Особенность оптимального пробоотбора — отбор точечных

проб в виде отдельных кусков массой q

, для чего, естественно,

должны быть разработаны соответствующие технические сред-

ства. Число точечных проб-кусков N отбирается равномерно от

всего опробуемого массива.

Для наглядности и сопоставительного анализа сведем полу-

ченные результаты в табл. 2.2.