Козин В.З. Исследование руд на обогатимость

Подождите немного. Документ загружается.

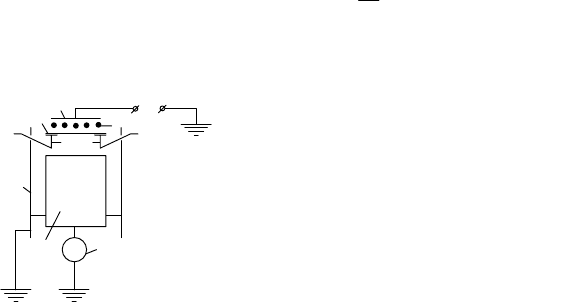
100

по вещественному составу, распределяются пополам (или в другой пропорции)

между концентратом и хвостами.

Экспериментальное измерение заряда частицы. Опытно измеряют за-

ряд единицы массы q

уд

(Кл/кг). Для этого заряжают пробу минерала и помеща-

ют ее в сосуд – цилиндр Фарадея (рис. 8.6).

Пробу 1 насыпают на заземленную площадку 2. Над площадкой распо-

ложен коронирующий электрод 3, на который от высоковольтного источника

подается напряжение U

. Цилиндр 4, расположенный внутри заземленного ме-

таллического корпуса 5, соединен с потенциометром 6. После заряда порошко-

образной пробы поворотом опор 7 площадки 2 сбрасывают пробу в зазор между

цилиндром и корпусом и измеряют потенциал U. Заряд пробы определяют так:

UCQ

⋅

Здесь Q – заряд, Кл; U – потенциал, В; C – электрическая емкость сосу-

да (цилиндр Фарадея), Ф (определяется заранее).

Удельный заряд частиц

уд

q =

где m – масса навески, кг.

Возможности использования заряда частиц при трибоэлектризации оце-

нивают, руководствуясь правилами:

- при контакте с металлом диэлектрик заряжается отрицательно;

- при контакте двух диэлектриков положительно заряжается диэлек-

трик с большей диэлектрической проницаемостью;

- при одинаковом химическом составе положительно заряжается тело с

более плотной структурой.

Величина заряда пропорциональна контактирующей поверхности.

8.11. Флотируемость

Флотируемость

частицы – это весьма сложный, не рассчитываемый по-

казатель.

В значительной степени флотируемость определяется краевым углом

смачивания, предопределяющим силу флотации (силу сцепления частицы с пу-

зырьком):

,θsinσ

жгkф

⋅

где d

- диаметр контакта частицы с пузырьком, м; σ

жг

- поверхностное натяже-

ние воды, 72,5

-3

Н/м; θ - краевой угол смачивания, град.

Рис. 8.6. К определению заряда

частиц

101

Экспериментально угол θ определяют прямым геометрическим измере-

нием: проецированием на экран нанесенной на минерал (частицу) капли жидко-

сти.

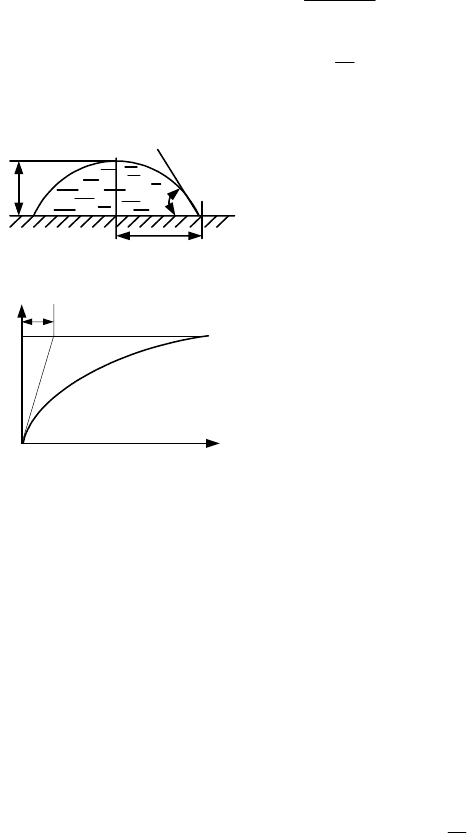
Можно угол θ определить по параметрам капли (рис.8.7, а):

при

90θ < cos

−

= ;

при

90θ > cos .1θ

−=

Здесь R – радиус капли.

Другой характеристикой флотируемости является

скорость флотации k, определяемая из уравнения кине-

тики флотации (рис. 8.7, б).

)e1(γγ

ββ

kt−

−=

∞

Флотируемость сростков предопределяется вели-

чиной k (или θ), соответствующей наиболее гидрофоб-

ной части сростка. В отличие от электрической сепара-

ции, в которой результат разделения связан с однократ-

ным (возможно, n - кратным) контактом частицы с оса-

дительным барабаном, при флотации частица имеет

возможность столкнуться с пузырьком воздуха много-

кратно и, в

итоге, та часть поверхности, гидрофобность

которой достаточна для прилипания к пузырьку, и пре-

допределит результат флотации. Другими словами

;θθ

maxср

Если в пульпе содержатся частицы с одинаковой скоростью флотации, то

величина k легко определяется по кривой кинетики флотации. Для этого нужно

провести касательную в начале экспоненты и найти отрезок T, отсекаемый ка-

сательной с линией

∞

γ , к которой стремится

γ . Тогда

−

= с

k .

Разработан ряд методик определения специфических величин и харак-

теристики процесса флотации:

- аппараты беспенной флотации для исследования взаимодействия реа-

гентов с межфазной границей твердое – жидкость;

- установки для измерения краевых углов смачивания;

- установки для определения времени прилипания частиц к пузырькам и

силы отрыва частиц от пузырьков;

- установки для определения поверхностного

натяжения на границе газ

– жидкость;

- установки для изучения состава поверхностных слоев реагентов на

границе раздела фаз;

- установки для измерения электродных потенциалов минералов, в том

числе ξ-потенциала, а также Eh и рH;

Рис. 8.7. К определению

краевого угла (

а) и

скорости флотации (

б)

∞β

102

- установки для измерения контактной и объемной поляризации мине-

ралов.

Измерение этих и других величин, характеризующих возможное пове-

дение частиц при флотации, позволяет объяснить это поведение и наметить на-

правления решения возникающих задач флотации. Однако уже в 1977 году

Л. А. Барский и Л. М. Данильченко опубликовали книгу «Обогатимость мине-

ральных комплексов»,

в которой перечислили возможные решения при флота-

ции тех или иных минералов [33].

Практика флотации показывает, что найденные решения не изменяются

многие десятилетия.

8.12. Растворимость

Растворимость минералов характеризуется скоростью растворения k

которая также определяется по кривой кинетики растворения:

(

)

еCC

−

−=

где С

– концентрация насыщенного раствора, мг/л; C – текущая концентрация,

мг/л; t

– продолжительность растворения, с.

Отсюда

()

/1ln

k −−=

При непрерывном выщелачивании в проточных условиях удобно изме-

рять скорость растворения в мг/ч⋅см

⋅

где

m∆ - убыль массы растворяемого минерала за время растворения t∆ ; S – по-

верхность растворяемого минерала, см

Так, например, скорость растворения золота в цианистых растворах при

промышленно используемых параметрах составляет 3 мг/ч⋅см

, что соответст-

вует линейной скорости растворения 1,5 мкм в час.

Растворимость сростков предопределяется долей доступной для раство-

рения поверхности минеральной частицы:

ср

= .

Здесь S

- поверхность растворяемого зерна минерала, освобожденного

от породы, доступная воздействию растворителя; S

– поверхность растворяе-

103

мого зерна минерала в сростке, доступная действию растворителя; q – скорость

растворения минерала, мг/ч⋅см

Растворимость как разделительный признак получает все большее рас-

пространение. Так начинают извлекать магний из серпентинитов, разработаны

технологии перевода в раствор всех компонентов сульфидных руд, пиритных

огарков и т. п. с последовательным извлечением из раствора Fe, Cu, Zn, Pb, Ag,

Tl, Se, Au.

104

Глава 9.

ФРАКЦИОННЫЕ ХАРАКТЕРИСТИКИ

9.1. γ и α функции и их использование

Фракционные характеристики – это значения выходов и массовой доли

компонентов для частей (фракций) руды или продуктов обогащения. При этом

фракцией называют часть продукта, для которой величина какого-либо разде-

лительного признака ограничена заданными значениями. Так, классы крупно-

сти – это фракции

крупности.

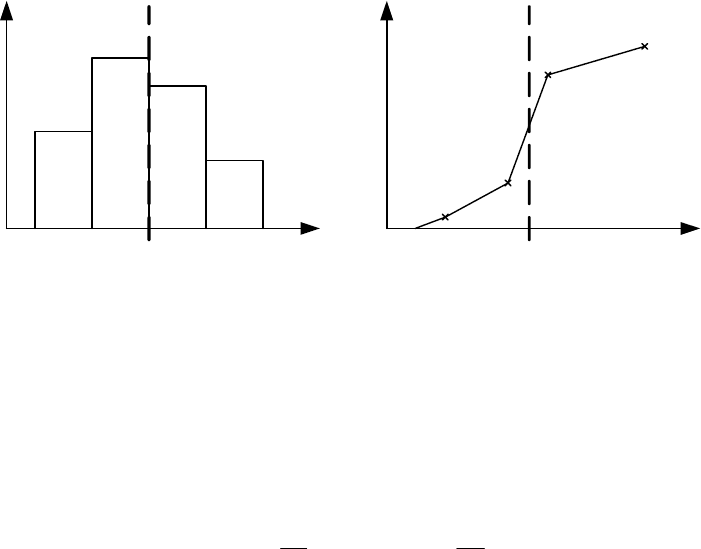
Фракционные характеристики наглядно представляют как выходы для

фракций разделительного признака (γ-функция) и зависимость массовой доли

определяемого компонента от величины разделительного признака (α-

функция).

Обозначим любой разделительный признак буквой ξ, а ξ

гр

– граничное

значение разделительного признака при делении руды на две фракции - кон-

центрат и хвосты, тогда γ и α функции будут выглядеть так, как на рис. 9.1.

max

гр

min

max

гр

min

Рис. 9.1. γ - функция (а) и α - функция (б)

По этим двум характеристикам можно рассчитать выход и качество

концентрата и хвостов для сепаратора с идеальной сепарационной характери-

стикой.

∑

max

γγ

гр

∑

гр

min

γγ

;

∑

max

αγ

гр

∑

гр

min

αγ

Этих характеристик и формул вполне достаточно для расчетов выходов

продуктов разделения, массовых долей компонента в них и соответствующих

им значений разделительных признаков, что эквивалентно построению для гра-

витационных процессов кривых обогатимости Анри – Рейнгардта и, естествен-

но, исключает их построение.

Для сепаратора с известной (неидеальной) сепарационной характери-

стикой

()

f ξε

105

∑

εγγ

;

∑

iii

εαγ

Так как величина разделительного признака и массовая доля компонен-

та в кусках непосредственно связаны с долей минерала в куске, т. е. от типа

сростков, то ясно, что как γ

)ξ( , так и

(

)

ξα меняются с изменением крупности

кусков. Другими словами, изменение крупности кусков является основным

средством изменения (преобразования) фракционных характеристик руды.

С изменением крупности меняется также возможный диапазон измене-

ния разделительного признака

minmax

ξξ

−

Для выбора разделительного признака либо оценки эффективности ка-

кого-либо разделительного признака при построении схемы разделения нужно

знать фракционные характеристики соответствующих классов крупности руды.

9.2. Предельные фракционные характеристики

Фракционные характеристики руд не являются постоянными. Они из-

меняются с изменением крупности. Предельным вариантом является фракци-

онная характеристика, построенная для d→0.

Такую фракционную характери-

стику и назовем предельной. Ее основной особенностью является то, что при

d→0 доля сростков стремится к нулю. Следовательно, предельная фракционная

характеристика строится для кусков руды, состоящих только из чистых мине-

ралов, и она может быть построена по справочным данным и по результатам

минералогического, а в некоторых случаях

и по данным элементного анализа.

Пусть руда состоит из кварца и пирита, причем доля кварца 70 % и пи-

рита 30 % по массе.

Для этих минералов в справочнике [20] можно найти следующие вели-

чины табл. 9.1.

Таблица 9.1

Значения возможных разделительных признаков

Минерал Формула

Плот-

ность ρ,

кг/м

Удельная маг-

нитная вос-

приимчи-

вость, м

/кг

Удельная

электро-

провод-

ность, См/м

Диэлек-

трическая

прони-

цаемость

Массо-

вая до-

ля же-

леза, %

Кварц SiO

2600 -0,02

-7

0,5

-14

4,4-6,0 -

Пирит FeS

4900-

5200

(0,02-0,1)

-7

-10 >81 46,5

По найденным характеристикам минералов можно построить предель-

ные фракционные характеристики. На рис. 9.2 представлены некоторые из них.

Предельная фракционная характеристика для двух минералов будет

представлена двумя столбиками, для представленного примера высотой 0,7 и

0,3 долей единицы, т. е. сумма выходов будет равна единице. Так как для мно-

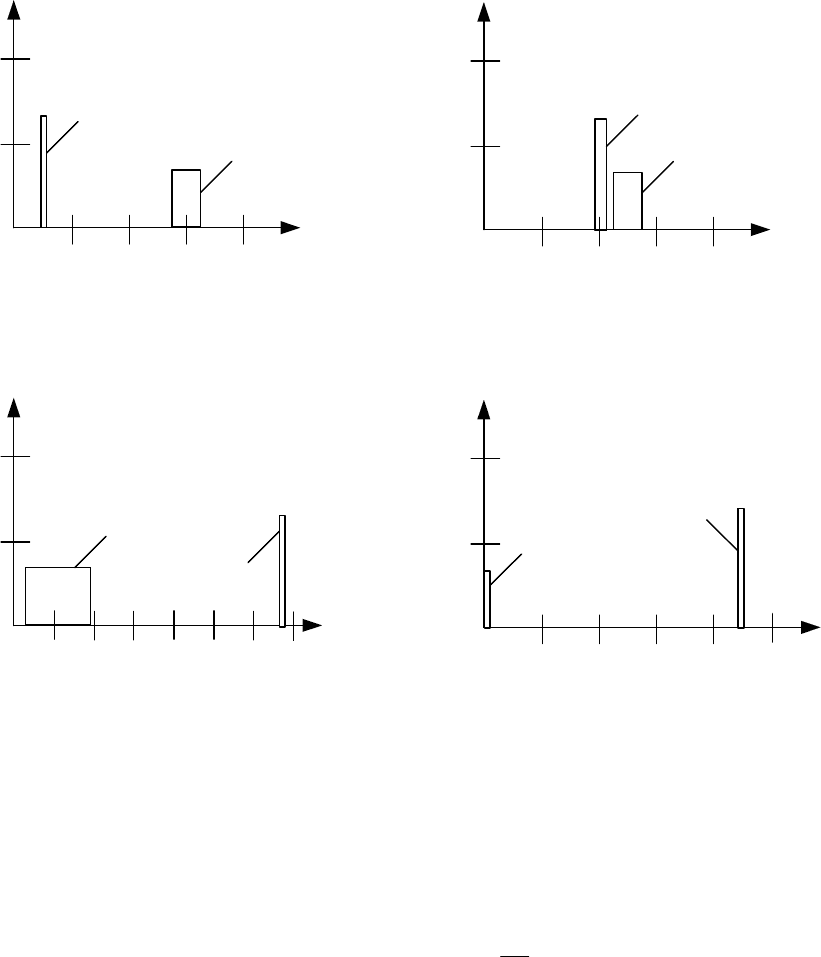
106

гих минералов разделительные признаки в таблице даны в виде некоторого

диапазона, отразим этот факт шириной столбика, соответствующий диапазону

разделительного признака, сохранив его высоту.

кг/м ρ,

40003000 5000 60002000

0,5

1,0

10/кгм ,

−

⋅

0-1 1 2-2

0,5

1,0

Пирит

Кварц

Пирит

Кварц

мОм ,

уд

⋅

-6

0,5

1,0

2010 30 400

0,5

1,0

Пирит

Кварц

Пирит

Кварц

-3

д. ед. д. ед.

Рис. 9.2 Предельные фракционные характеристики для руды, состоящей из двух минералов:

а – по плотности; б – по удельной магнитной восприимчивости; в – по удельному сопротив-

лению;

г – по информационному сигналу «массовая доля железа».

При минералогическом анализе определяют непосредственно массовую

долю минерала в руде

мм

γα = ; при элементном анализе, если элемент связан с

одним минералом, массовую долю минерала в руде можно найти по формуле

мм

αγ ==

где

α - массовая доля элемента в руде;

β - массовая доля элемента в минерале.

α - функции для предельных фракционных характеристик не изобража-

ют, так как речь идет о выделении минералов.

Некоторые из разделительных признаков, например флотируемость,

растворимость, в минералогических справочниках не указываются, так как они

являются поверхностными и могут быть изменены изменением поверхности

частиц. Значения скорости флотации, в частности,

могут быть получены (оце-

нены) только по результатам флотации этих минералов при определенных ре-

107

жимах. Предельные фракционные характеристики для таких условий обычно не

строят, а изменением условий разделения добиваются максимального различия

в выбранном разделительном признаке для выделяемого минерала по сравне-

нию с остальными.

Существуют рассчитываемые по справочным данным разделительные

признаки, например термодинамический СВЧ-фактор, скорость витания. Сле-

довательно, перед построением предельной фракционной характеристики их

необходимо

рассчитать.

Наконец, такой разделительный признак, как крупность частиц, рас-

сматривается вначале как физический признак и становится разделительным

при наличии благоприятной зависимости массовой доли выделяемого компо-

нента от крупности.

Фракционные характеристики позволяют оценить возможности исполь-

зования разделительных признаков при обогащении. Так, представленные

фракционные характеристики для пирита и кварца показывают, что для

разде-

ления этих двух минералов наилучшим разделительным признаком являются

удельная проводимость и информационный сигнал, возможно использование

различия в плотности частиц и нереально использование магнитных свойств.

Так как возможности использования разделительных признаков зависят

от крупности, то при оценке этих возможностей можно рассчитать фракцион-

ные характеристики для классов крупности, содержащих сростки.

Это идеально

простая ситуация. Для реальной руды предельные фрак-

ционные характеристики будут более сложными.

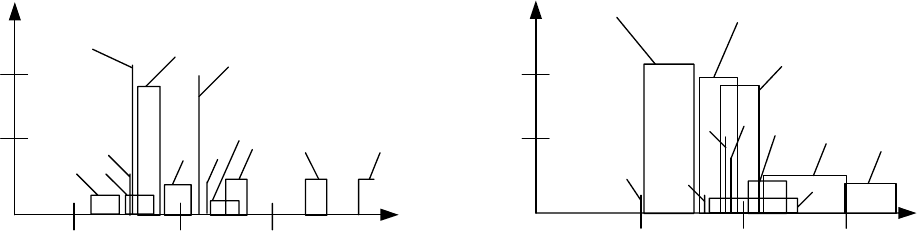
Приведем в качестве примера предельные фракционные характеристики

для флюоритовой руды (рис. 9.3) [34].

кг/м ρ,

4000

3000

2000

SiO

CaСO

3 CaF

BaSO

FeS

8412

SiO

CaF

CaСO

BaSO

0,1

0,2

0,1

0,2

д. ед.

Рис. 9.3. Фракционная характеристика флюоритовой руды по плотности –

а и диэлектриче-

ской проницаемости –

б:

γ – выход или массовая доля минерала; 1 – цеолит; 2 – полевые шпаты; 3 – каолинит;

4 – слюда; 5 – апатит; 6 – эпидот; 7 – хлорит

Предельные фракционные характеристики для раскрытой руды позволяют

наметить возможную схему обогащения. Так, для серебряно-медной руды, ко-

торая раскрывается, начиная с крупности 5 мм, получены предельные фракци-

онные характеристики (рис. 9.4), из которых следует такая схема обогащения

(рис. 9.5).

108

мОм

уд

⋅

-6

-4

-2

10/кгм ,

−

⋅

4 8 12 16 20 24 28

д. ед.

Рис. 9.4 Фракционная характеристика серебряно-медной руды по удельной магнитной вос-

приимчивости –

а; по удельному сопротивлению – б:

1 – висмут; 2 – алевролит, аргиллит; 3 – пирит; 4 – арсенопирит; 5 - халькопирит; 6 – тетра-

эдрит;

7 – сидерит

Руда

МС

Сидерит

Нагрев

ЭС

МС

Серебряный

концентрат

Медный

концентрат

Висмутовый

концентрат

Алевролит

Аргиллит

Алевролит

Рис. 9.5 Схема разделения с использованием двух разделительных признаков:

МС

– магнитная сепарация; ЭС – электрическая сепарация

Достоинством такой схемы является сухое обогащение в крупности, при

которой эффективно использование как магнитных, так и электрических мето-

дов.

109

9.3. Предельная обогатимость руд

На любом этапе исследования и обогащения руды возникает вопрос о

предельных возможностях использования руды, т. е. какого качества и в каком

количестве могут быть получены концентраты.

При условии 100 % раскрытия руды и 100 % извлечения предельные

фракционные характеристики дают непосредственно ответ на этот вопрос: из

руды может быть извлечен концентрат

i-го минерала качеством β

и выходом

Это и будет теоретический предел обогащения.

Заметим, что реальные фракционные характеристики позволяют вычис-

лить реальные, но не предельные показатели обогащения.

Цыпин Е. Ф. [35] различает безусловно идеальное разделение, когда

массовая доля извлекаемого компонента в хвостах равна нулю (υ=0), и выход

концентрата

γ =

и идеальное разделение с ограничениями, когда в хвосты

все же попадает полезный минерал υ= υ

.Здесь υ

– заданное значение массовой

доли извлекаемого компонента в хвостах

Тогда выход концентрата идеального качества будет

зм

−

= ,

что, естественно, более реалистично, но на этапе оценки предельных возмож-

ностей по фракционным характеристикам υ

может быть назначено лишь ори-

ентировочно.

Еще более реалистично задавать не β

а β

, но это уже будет не идеаль-

ное разделение, а показатели не предельными.

Кроме этих теоретически предельных показателей (качество концентра-

та и его выход) необходим ответ на вопрос, при какой крупности руды возмож-

но достижение теоретически предельных показателей. Для ответа на этот во-

прос необходимо построение фракционных характеристик для различных клас-

сов крупности руды. Искомая крупность будет соответствовать той крупности,

для которой фракционная характеристика для извлекаемого минерала превра-

тится в δ-функцию (т. е. изолированный столбик) (рис. 9.6).

функцияδ−

для извлекаемого

минерала

(остальные минералы)

Не для всех разделительных признаков такое построение возможно, в

частности, для флотационного разделения.

Рис. 9.6 Фракционная характеристика руды

по плотности для класса крупностью –

при обогащении которого возможно полу-

чение предельных показателей γ

и β