Kozen D.C. Theory of Computation

Подождите немного. Документ загружается.

Berlekamp’s Algorithm 97

Chinese remainder theorem there is an isomorphism

[x]/f

∼

[x]/f

×···×GF

[x]/f

∼

×···×GF

(D.1)

given by the map

σ : GF

[x]/f → GF

[x]/f

×···×GF

[x]/f

σ(g)

def

=(g mod f

,... ,g mod f

The elements g ∈ GF

[x]/f are represented as polynomials in Z

[x, y]

modulo h and f.

Consider the subalgebra GF

of (D.1), where p is the characteristic. This

is an algebra of dimension n over GF

and contains exactly p

elements.

Its preimage under σ is the subalgebra

def

= {g | g mod f

∈ GF

, 1 ≤ i ≤ n} = {g | g

≡ g (mod f )}

of GF

[x]/f. This follows from the fact that the automorphism a → a

ﬁxes every element of GF

and moves every element not in GF

,andmul-

tiplication in (D.1) is componentwise, so this map applied to (D.1) ﬁxes

exactly the elements of GF

. Because the coeﬃcients of g as a polyno-

mial in GF

[x, y] are ﬁxed by a → a

, this is equivalent to the condition

g(x, y)

= g(x

). By computing all the powers x

modulo f and h

for i ≤ m and j ≤ k by repeated squaring and reducing modulo f and h,

then equating the coeﬃcients of g(x, y)andg(x

), we obtain a system of

linear equations in the indeterminate coeﬃcients of g(x, y)overZ

,which

we know how to solve in polynomial time by Gaussian elimination. This

allows us to determine n and compute a basis for the subspace A over Z

In particular, f is already irreducible iﬀ n =1.

If n>1, for any polynomial g ∈ A,wehave

σ(g)=(a

,... ,a

)

with a

∈ GF

,1≤ i ≤ n.Wedonotknowthea

, but we know that they

exist. If we can get our hands on a g ∈ A such that at least one a

and at least one a

= 0, then we get a nontrivial factorization, because

≡ g mod f

=0iﬀf

divides g,sof and g would have a nontrivial

common factor, which can be found by computing the gcd.

If the characteristic is small enough, we can solve the problem deter-

ministically: just pick an element g ∈ A of degree at least 1, so that it is not

in Z

, then consider the elements g − a for a ∈ Z

. One of these must work.

Because g ∈ Z

, there must be some a

= a

in σ(g), thus σ(g − a

)is0in

position i and nonzero in position j. This gives a nontrivial factorization.

If the characteristic is large, here is how to get such a g with high

probability. Pick an  ∈ A at random and take

g = 

(q−1)/2

− 1modf.

98 Supplementary Lecture D

We pick  ∈ A at random by picking a random linear combination of the

basis for A. We compute the appropriate power of  modulo f by repeated

squaring and reducing modulo f.

We now show that the chances are about even or better that g and f

have a nontrivial common factor. Because the characteristic is odd, exactly

half the nonzero elements of GF

are squares; that is, elements of the form

for some b ∈ GF

. The squares are exactly the roots of x

(q−1)/2

−1. If  is

chosen at random, and if σ()=(a

,... ,a

), then for each i we have about

an even chance that a

is a square, and these events are independent. Thus

we have about an even chance or better that at least one a

is a square and

at least one is not. Computing 

(q−1)/2

−1, we get 0 in location i iﬀ a

was

asquare.

To reduce the problem deterministically to the case in which f splits

into linear factors over GF

,pickg ∈ A of degree at least 1. Thus if

σ(g)=(a

,... ,a

), not all the a

are equal. The elements a

are exactly

the elements a ∈ GF

such that g−a and f have a root in common, because

σ(g − a)=(a

− a,... ,a

− a),

which has a 0 in position i iﬀ a = a

iﬀ f

divides g − a.Thusthea

are

all the roots of the resultant

r(z)=Res

(g(x) − z,f(x))

lying in GF

(see [64, 75] for an introduction to resultants). We can pick

out the roots of r lying in GF

by taking the gcd of r(z)andz

q−1

−1. This

is done by computing r(z) ﬁrst, which is of degree m, then computing z

q−1

modulo r by repeated squaring and reducing modulo r to get a low-degree

polynomial s, then taking the gcd of s − 1andr.

After removing repeated roots as above, the resulting polynomial is of

degree at most m and splits into linear factors over GF

.Moreover,ifa is

any root of this polynomial, then the gcd of f and g −a will be a nontrivial

factor of f. We have thus reduced the problem of factoring a polynomial

of degree m to the problem of factoring a polynomial of degree at most m,

all of whose roots lie in the prime ﬁeld.

Lecture 15

Interactive Proofs

In the next few lectures we take a look at a model of computation involving

interactive protocols between two agents. One of the agents wants to convey

some information to the other, and the other wants to be convinced with

a high degree of certainty that the information is correct. Such protocols

arise in cryptography and message authentication.

Polynomial-time interactive protocols give rise to a complexity class IP.

Whereas we can think of a set in NP as a set of theorems admitting short

proofs,wecanthinkofasetinIP as a set of theorems having eﬃcient

interactive proofs.

Interactive Proof Systems

The machine model consists of two independent Turing machines P (the

prover)andV (the veriﬁer). The two machines share a common read-only

input tape and a read/write communication tape, but otherwise operate

independently. Each machine has its own private worktape. We assume in

addition that

• V has access to a private string of random bits;

• V runs in polynomial time; and

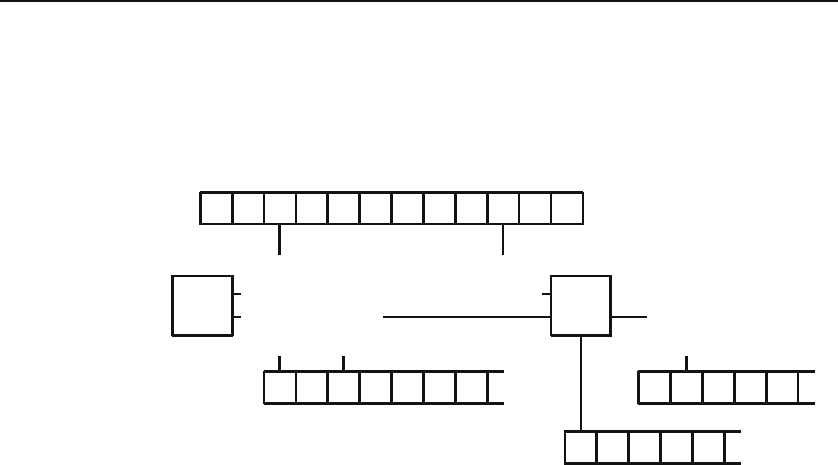
100 Lecture 15

• P is not bounded in time or space, but must halt on all inputs and

may only write strings of polynomial length on the communication

tape. In fact, we could even have deﬁned P to be some kind of oracle

or black box computing some noncomputable function—the exact

nature of P does not really matter.

 abbabaaaab

input, read only

 aababb ···

communication, r/w

 0110 ···

random bits

 aaba ···

work, r/w

P V

The two machines alternate. When it is V ’s turn, it runs for polynomial

time, accessing its random bits whenever it needs to make a probabilistic

decision. At some point it writes a message to P on the communication

tape and enters a special state that causes control to transfer to P .The

machine P then runs for as long as it likes, reading the message from V

and eventually writing a message back to V of polynomial length on the

communication tape and transferring control back to V . Control passes

back and forth between the two agents for some polynomial number of

rounds determined by V ,afterwhichV decides whether to accept or reject.

We can think of P as trying to convince V that the input string satisﬁes

some property, and of V as trying to verify that that information is correct.

When that property is indeed true of the input string, it should be possible

for P to convince V of that fact with high probability. By accepting, V

indicates that it is convinced that the property is true.

Now imagine substituting an evil intruder P



for P . Let us say that V

runs its part of the protocol as before, but P



may behave diﬀerently from

P .Inparticular,P



might try to convince V that the property of interest

holds of the input string when in fact it does not. The veriﬁer V should

be able to detect this type of dishonest behavior with high probability and

reject.

The formal deﬁnition is as follows.

Deﬁnition 15.1 The protocol (P, V ) is an interactive proof system for a set of strings A if

for all x,

Interactive Proofs 101

• if x ∈ A,then

((P, V ) accepts x) ≥

• and if x ∈ A, then for any P



((P



,V) accepts x) ≤

where the probability is with respect to the random bits y chosen uniformly

from the set of all strings of some length exceeding the polynomial time

bound of the veriﬁer.

AsetA is in IP if it has an interactive proof system.

The constants

and

in Deﬁnition 15.1 are inconsequential. By ampli-

ﬁcation, we could specify 1 −ε and ε for any ε>0 (Miscellaneous Exercise

44).

Examples of Interactive Proofs

The best way to get a feel for this model is to look at some examples.

Example 15.2 Boolean satisﬁability (and in fact, any set A ∈ NP)isinIP, because there

is a one-round protocol that does not use any random bits. The prover

would like to convince the veriﬁer that a given Boolean formula written on

the input tape is satisﬁable. The prover just sends the veriﬁer a satisfying

assignment if one exists. Because the prover is not restricted by any time

bound, it can search exhaustively for a satisfying assignment and send

the ﬁrst one it ﬁnds to V . If no satisfying assignment exists, it just sends

something arbitrary. The veriﬁer then evaluates the input formula on the

truth assignment communicated by P . If the formula is satisﬁed, then V

accepts; if not, it rejects.

Now if the given formula really is satisﬁable, then (P, V ) accepts with

probability 1. The veriﬁer is completely convinced, because it has a proof

in the form of a satisfying assignment. On the other hand, if the formula is

not satisﬁable, then no prover P



, regardless of how clever or malicious it

is, can convince V otherwise. In this case, (P



,V) accepts with probability

0. 2

Example 15.3 Here is an example due to Goldreich, Micali, and Wigderson [48] that is a

bit more complicated: graph nonisomorphism is in IP. This is interesting,

because graph isomorphism is in NP (given a pair of graphs, guess an

isomorphism and verify that it is an isomorphism in polynomial time), but

it is not known to be in co-NP.

Here is an IP protocol for graph nonisomorphism. The input is an

encoding of two graphs G, H on n vertices. The following procedure is

executed k times.

102 Lecture 15

(i) The veriﬁer V chooses a random permutation of {1, 2,... ,n}.This

requires roughly n log n random bits. It applies the permutation to

the vertices of the graphs G and H to get G



and H



, respectively.

Then V ﬂips a coin. If it comes up heads, it sends G



to P , and if it

comes up tails, it sends H



to P .

(ii) The prover P checks whether G on its input tape and the graph

sent to it by V are isomorphic, say by exhautively searching

for an isomorphism, and communicates its ﬁnding—isomorphic or

nonisomorphic—honestly to V .

(iii) V takes the following action based on its coin ﬂip and the prover’s

response.

If the ﬂip is and P responds then do this

heads isomorphic continue

heads nonisomorphic reject immediately

tails isomorphic reject immediately

tails nonisomorphic continue

If the protocol makes it all the way through k rounds, then V accepts,

convinced with a high degree of certainty that G and H are not isomorphic.

Now let us argue that V has good reason to be convinced. Suppose

that G and H really are not isomorphic. The prover P , because it plays

honestly, will always answer “isomorphic” when passed a permutation of G

and “nonisomorphic” when passed a permutation of H, so the second and

third rows of the table will never occur. The protocol will make it through

all k rounds successfully and V will accept with probability 1.

On the other hand, suppose G and H are isomorphic. In each round, V

will send the prover a random permutation of G or H, depending on the

result of its coin ﬂip, but the prover cannot tell the diﬀerence. It cannot

see V ’s random bits or worktape; it must make its decisions purely on

the basis of the message from V . A dishonest prover P



,tryingtofoolV

into erroneously accepting, must respond “nonisomorphic” whenever V ’s

ﬂip was tails and “isomorphic” whenever V ’s ﬂip was heads, but there

is no way it can tell which of these two events occurred. The chances of

accidentally choosing the correct alternative k times in a row are 2

−k

. 2

In the next two lectures we prove a remarkable theorem: IP = PSPACE .

Interactive proof systems and the class IP were deﬁned by Goldwasser,

Micali, and Rackoﬀ [49]. A related model, called Arthur–Merlin games,was

deﬁned by Babai [8].

Lecture 16

PSPACE ⊆ IP

In this lecture we show that any set in PSPACE has an IP protocol. This

result is due to Shamir [111], based on work of Lund, Fortnow, Karloﬀ, and

Nisan [81].

It suﬃces to show that the QBF problem has an IP protocol. That is,

given any quantiﬁed Boolean formula B,ifB is true then the prover P can

convince the veriﬁer V of that fact with high probability, and if B is false

then no prover P



can convince V that B is true with more than negligible

probability.

The proof consists of several steps.

1. We ﬁrst show how to transform the given formula into a special simple

form.

2. We then transform a simple Boolean formula B into an arithmetic

expression A by replacing the Boolean operators with arithmetic op-

erators. The arithmetic expression A represents a nonzero value iﬀ

the Boolean formula B is true. This step is called arithmetization.

3. We reduce the problem to determining whether an arithmetic expres-

sion A is zero modulo a suﬃciently large prime p.Thisstepusesthe

Chinese remainder theorem and the fact that primality is in NP,as

shown previously in Lectures B and C.

104 Lecture 16

4. Finally, we describe a protocol for the prover to convince the veriﬁer

with high probability that an arithmetic expression A vanishes mod-

ulo p. The protocol consists of several rounds and is inductive on the

structure of A.

Step 1

Deﬁnition 16.1 A quantiﬁed Boolean formula B is simple if negations are applied only to

variables, and for every subformula of the form ∃xC(x) or ∀xC(x) of B,

any free (unquantiﬁed) occurrence of x in C(x) occurs in the scope of at

most one universal quantiﬁer ∀y in C(x). In other words, there is at most

one ∀y between any occurrence of a variable and its point of quantiﬁcation.

For example, the Boolean formula

∀x ∀y ∃z ((x ∨ y) ∧∀w (¬y ∨z ∨ w)) (16.1)

is simple, whereas the formula

∀x ∀y ∃z ((x ∨ y) ∧∀w (¬x ∨ z ∨ w)) (16.2)

is not, because the second occurrence of x occurs in the scope of both the

∀w and the ∀y, both of which occur in the scope of the ∀x. In the formula

∀x ∀y ∀zF(x, y, z),

if x occurs free in F(x, y, z), then the formula is not simple.

Lemma 16.2 Every quantiﬁed Boolean formula can be put into simple form by a logspace

transducer with at most a quadratic blowup in size.

Proof. First move all negations inward using the two De Morgan laws

¬(x ∨ y)=¬x ∧¬y and ¬(x ∧ y)=¬x ∨¬y, the law of double negation

¬¬x = x, and the quantiﬁer rules ¬∀xϕ = ∃x¬ϕ and ¬∃xϕ = ∀x¬ϕ.This

allows us to assume without loss of generality that all negations are applied

only to variables.

Now for every subformula of the form

∀xC(x, y

,... ,y

), (16.3)

where y

,... ,y

are the free variables of (16.3) (that is, they are quanti-

ﬁed outside the subformula (16.3)), introduce new variables y



,... ,y



and

replace (16.3) with

∀x (∃y



...∃y





i=1

↔ y



) ∧ C(x, y



,... ,y



)) (16.4)

PSPACE ⊆ IP 105

in the original formula. Do this from the outside in, larger subformulas

ﬁrst. For example, applying this transformation to (16.2) would yield

∀x ∀y ∃x



((x ↔ x



) ∧∃z ((x



∨ y)

∧∀w ∃x



∃z





↔ x



) ∧ (z



↔ z) ∧ (¬x



∨ z



∨ w))).

In (16.4), the variables y

now occur exactly once each, just inside the ∀x.

Occurrences of y

in C are replaced by y



, which are quantiﬁed inside the

∀x. 2

The reason for this transformation becomes apparent when we do the arith-

metization. It leads to polynomials of low degree.

Step 2 This is the arithmetization step. Suppose we have a simple quan-

tiﬁed Boolean formula B. Change this to an arithmetic formula A with

variables ranging over the integers Z as follows.

• Replace each negative literal ¬x with 1 − x.

• Keep each positive literal x as it is.

• Replace each ∧ by · (multiplication).

• Replace each ∨ by +.

• Replace each ∃x by



x∈{0,1}

. The expression



x∈{0,1}

C(x)isjusta

succinct way of writing C(0) + C(1) without having to duplicate the

subexpression C.

• Replace each ∀x by



x∈{0,1}

. The expression



x∈{0,1}

C(x)isjusta

succinct way of writing C(0) · C(1).

Let A be the resulting arithmetic expression. For example, if B is the simple

formula (16.1), then A would be



x∈{0,1}



y∈{0,1}



z∈{0,1}

((x + y) ·



w∈{0,1}

(1 − y + z + w)). (16.5)

106 Lecture 16

Each such expression denotes a number obtained by evaluating the expres-

sion. For example, (16.5) evaluates to



x∈{0,1}



y∈{0,1}



z∈{0,1}

((x + y) ·



w∈{0,1}

(1 − y + z + w))



x∈{0,1}



y∈{0,1}



z∈{0,1}

(x + y)(1 − y + z)(2 −y + z)



x∈{0,1}



y∈{0,1}

(x + y)(1 − y)(2 −y)+(x + y)(2 −y)(3 − y)



x∈{0,1}

16x(x +1)

=0.

Because the arithmetic formula evaluates to 0, the original quantiﬁed

Boolean formula (16.1) was false.

Step 3 Because of the operators



and



, these arithmetic expressions

can be too costly to evaluate directly. The value of the expression can be

as big as 2

,wheren is the size of the original formula; for example,



...



2=2

However, we can also prove by induction on the depth of the expression

that 2

is an upper bound on the value. Thus, using the Chinese remainder

theorem (Theorem B.1), we can show that the expression is nonzero iﬀ it

is nonzero modulo some prime p,wherep canbewritteninbinaryusing

polynomially many bits.

The task for the prover is therefore reduced to providing a small (n

bit) prime p and a nonzero value a ∈ Z

∗

= Z

−{0} and convincing the

veriﬁer that

(i) p is prime, and

(ii) the arithmetic expression A − a vanishes modulo p.

Proving that p is prime is easily done in one round using the fact that

primes are in NP (Theorem C.4).

Step 4 We must show how to convince the veriﬁer that an arithmetic

expression A vanishes modulo p,wherep is a prime of polynomially many

bits. Let Z

denote the ﬁeld of integers modulo p. We can also assume

without loss of generality that p ! n.