Косчинский С. Л., Косчинская Е. В. Основы автоматики и систем автоматического управления
Подождите немного. Документ загружается.

4.
Лабораторная работа № 4 “Исследование систем автоматического
регулирования с широтно-импульсной модуляцией”
4.1 Цель работы.
Получить практические навыки исследования и проектирования импульсных САУ.
4.2 Краткие теоретические сведения.
Система автоматического управления называется дискретной, если в ней осуществляет-
ся дискретизация сигнала рассогласования, т.е. непрерывное управление заменяется на дис-
кретное.
Дискретные САУ делятся на классы:
1. Релейные (дискретизация сигнала рассогласования (квантование) по уровню)
• Чистые релейные;
• Релейно-импульсные.
2. Импульсные (дискретизация (квантование) по времени)
• САУ с амплитудно-импульсной модуляцией (АИМ);
• САУ с широтно-импульсной модуляцией (ШИМ);
• САУ с частотно-импульсной модуляцией (ЧИМ);
3. Цифровые (дискретизация (квантование) по времени и по уровню)
Типовая структурная схема дискретной САУ представлена на рис. 4.1. Импульсные
САУ являются наиболее широко используемыми в настоящее время, благодаря их высокой
энергетической эффективности (высокий к.п.д.), очень хорошим массогабаритным показате-
лям и пр.
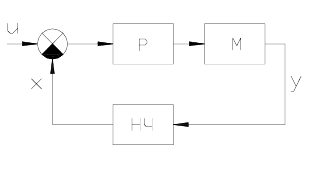
ε
σ
Рис. 4.1 Дискретная САУ: Р - регулятор; М - модулятор;
НЧ - непрерывная часть (объект управления).
Основным элементом импульсной САУ является модулятор (рис. 4.1), собственно и
реализующий дискретизацию сигнала рассогласования по времени или модуляцию. Процесс
модуляции сигнала рассогласования в САУ с ШИМ, например, заключается в сравнении это-
го сигнала в компараторе с некоторым другим опорным периодическим сигналом (как пра-
вило пилообразной или треугольной формы). При этом ширина импульсов на выходе компа-
ратора пропорциональна амплитудному значению сигнала рассогласования.
Для любой импульсной САУ различают вид, род, и тактность модуляции. Вид модуля-
ции определяется тем, какой параметр подвергается модуляции и несёт полезную информа-
цию (например, для САУ с ШИМ модуляции подвергается ширина импульсной последова-
тельности на выходе модулятора, для САУ с ЧИМ - частота). Род модуляции определяется
способом формирования импульсной последовательности на выходе модулятора. Существу-
ют модуляции 1-го и 2-го рода, сущность которых достаточно очевидна из рис. 4.2.
Тактность модуляции – связана с характером формирования импульсной последова-
тельности – с полярностью формируемых импульсов. Различают однотактные и двухтактные
САУ.
В настоящее время наиболее широко распространенными дискретными САУ являются
САУ с ШИМ. Для САУ с ШИМ в зависимости от способа реализации модулирующей после-
довательности различают: модуляцию заднего фронта, модуляцию переднего фронта и двух-
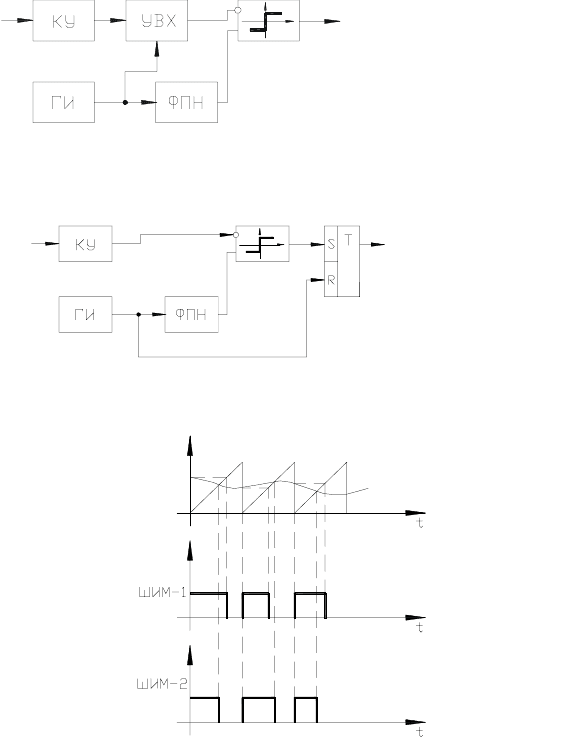
стороннюю модуляцию. Пример модуляции заднего фронта рис. 4.2в.
σ
а) ШИМ модулятор 1-го рода
σ
б) ШИМ модулятор 2-го рода.
в) временные диаграммы, поясняющие принцип ШИМ 1-го и 2-го родов.
Рис.4.2 Модуляторы ШИМ: КУ - корректирующее устройство (регулятор),
УВХ - устройство выборки хранения, ГИ - генератор импульсов,
ФПН - формирователь пилообразного напряжения.
В качестве примера САУ с ШИМ на рис. 4.3 приведена САУ тока двигателя постоянно-
го тока.

U
у
β
α
R
L
E( )i
дв
U
0
u
дв
+
+
-
-
i
дв
ФПН
Т
R
S
модулятор
объект управления
(двигатель)
компаратор
усилитель
ошибки
масштабный
усилитель
i
вх
i
д
K
f
ε
αε
Рис. 3 САУ с ШИМ тока двигателя постоянного тока.
Временные диаграммы, поясняющие принцип работы САУ рис.4.3 приведены на
рис.4.4.
αε
K
f
u
дв
i
дв
i
вх
i
д
t
t
t
t
t
t
Рис. 4.4 Временные диаграммы, поясняющие принцип работы САУ с ШИМ на рис. 4.3.
Установившимся движением в САУ с ШИМ являются периодические колебания (см.
диаграммы на рис. 4.4). Параметры данных периодических колебаний определяют статиче-
ские показатели качества САУ с ШИМ в целом (например, статическую ошибку, величину
пульсаций и пр.). Соответственно, задача анализа САУ с ШИМ сводится к задаче нахожде-

ния параметров периодических колебаний для различных значений нагрузки.
Алгоритм нахождения периодических колебаний в САУ с ШИМ следующий:
1. Из принципа работы схемы, определяем число возможных состояний постоянства
структуры САУ, характеризующихся определенным состоянием (замкнуто/разомкнуто) клю-
чевых элементов САУ. Например, для схемы рис. 4.3 существуют два состояния постоянства
структуры: потребление энергии от питающей сети; и состояние «свободного хода», при ко-
тором САУ отключена от сети (рис. 4.5).
R
L
E( )i
дв
U
0
+
-
i
дв
а)
R
L
E( )i
дв
i
дв
б)
Рис. 4.5 Состояния постоянства структуры для САУ с ШИМ рис. 4.3.
2. Для каждого из состояний постоянства структуры составляем математическую мо-
дель в форме дифференциальных уравнений. Для рассматриваемой САУ эта модель для каж-
дого состояния постоянства структуры представляет собой одно дифференциальное уравне-
ние первого порядка вида
di
дв
/dt = Ai
дв
+B
1
для рис. 4.5а,(4.1)
di
дв
/dt = Ai
дв
+B
0
для рис. 4.5б. (4.2)
где
A, B
1
, B
0
- коэффициенты, определяемые параметрами элементов САУ.
Момент перехода системы с состояния рис. 4.5а на состояние рис. 4.5б (момент комму-
тации t
k
) описывается уравнением коммутации x(i
дв
, t
k
)=0, описывающем модулятор.
Для САУ рис. 4.3 (ШИМ-2) уравнение коммутации имеет вид:
α
(Uy-
β⋅
i
дв
(t
k
))-U
0
t
k
/T=0, t
∈
[0; T]. (4.3)
Для модулятора с ШИМ-1 данное уравнение имеет вид:
α
(Uy-
β⋅
i
дв
(0))-U
0
t
k
/T=0, t
∈
[0; T]. (4.4)
В уравнениях (4.3)-(4.4) U
0
- амплитуда опорного пилообразного напряжения.
Отличие (4.3) от (4.4) заключается в том, что в уравнении (4.4) значение переменной i
дв
рассматривается в фиксированный момент времени (в начале периода), а в уравнение (4.3)
переменная i
дв
входит как функция времени. При анализе импульсных САУ часто вместо ве-
личины t
k
используют понятие коэффициента заполнения импульса на периоде ШИМ
γ
k
, оп-
ределяемого как
γ
k
=t
k
/T. Также
γ
k
называют углом открытия ключа.
3. Рассмотрим один период искомого периодического движения kT<t<(k+1)T (рис. 4.6).
Пусть на интервале kT<t<t
k
состояние системы определяется рис.4.5а, а на интервале
t
k
<t<(k+1)T состояние системы определяется рис. 4.5б. Поскольку установившее движение
периодическое, то i
дв
(kT)= i
дв
((k+1)T).
Записав решение системы в общем виде для интервала времени kT<t<t
k
(система рис.
4.5а) и подставив в него значение t
k
из уравнения коммутации, получим в общем виде выра-
жение i
дв
(t
k
)=f(i
дв
(kT)).
Аналогично, записав решение системы в общем виде для интервала времени
t
k
<t<(k+1)T (система рис. 4.5б) и подставив в него значение i
дв
(t
k
), получим в общем виде вы-
ражение i
дв
((k+1)T)=f(i
дв
(kT)). Из условия периодичности полученное выражение будет вы-
глядеть как x*=f(x*). Решение x* может быть получено как аналитически, так и графически.
4. Зная значение i
дв
(kT)= i
дв
((k+1)T)=x* мы можем найти t
k
и i
дв
(t
k
). Тогда приближенное
среднее значение i
дв
будет определяться как (i
дв
(t
k
)+i
дв
(kT))/2, а величина пульсаций регули-
руемой переменной в установившемся режиме будет определяться как i
дв
(t
k
)-i
дв
(kT).
Для рассмотрения статических свойств САУ с ШИМ используют так называемые регу-

лировочные характеристики. Т.е. зависимости среднего значения регулируемой величины и
амплитуды пульсаций от коэффициента заполнения импульса на периоде ШИМ γ
k
.
4.3 Описание лабораторной работы.
1. Получить у преподавателя значения параметров для рассматриваемой САУ с ШИМ
(рис.4.1). Составить математические модели для интервалов постоянства структуры САУ.
2. Считая, что нагрузка САУ приведена к валу двигателя (различной нагрузке будут со-
ответствовать различные скорости вращения вала) построить регулировочные характеристи-
ки для различных значений скорости. При этом полагать, что в САУ используется модулятор
с ШИМ-1, а ЭДС вращения двигателя приближенно определяется зависимостью
E(i
дв
)=n
⋅
r
⋅
i
дв
, где n- скорость вращения вала двигателя, а r параметр аппроксимации кривой
намагничивания двигателя. Полученные в процессе расчетов данные свести в табл. 4.1.
Таблица 4.1
Результаты расчетов параметров установившихся колебаний в САУ с ШИМ
скорость вращения вала,
об/мин
200 400 600 800 1000 1200 1400 1600
i
дв
(kT)
t
k
γ
k
среднее значение <i
дв
>
амплитуда пульсаций ∆i
дв
3. По данным табл. 4.1 построить регулировочные характеристики САУ с ШИМ
<i
дв
>=f(γ
k
) и ∆i
дв
=f(γ
k
).
4.4 Контрольные вопросы.
1. Опишите алгоритм поиска периодических колебаний в импульсных САУ? Для чего
осуществляется поиск периодических колебаний?
2. В чем заключаются преимущества и недостатки САУ с ШИМ по сравнению с релей-
ной САУ?
3. К какому классу систем относится рассматриваемая САУ к классу статических или
астатических? Почему?
4. Как изменяться регулировочные характеристики САУ если увеличить коэффициент
усиления регулятора
α
? Почему? Проведите аналогию с непрерывными системами.
5.
*
Как на Ваш взгляд изменяться регулировочные характеристики если использовать в
рассматриваемой САУ модулятор ШИМ-2 вместо модулятора с ШИМ-1?
Литература
1. Теория автоматического управления. В 2-х частях. Ч.1. Теория линейных систем ав-
томатического управления. /Под. ред. А.А. Воронова. – М.: Высшая школа, 1986. – 367 с.
2. Попов Е.П. Теория линейных систем автоматического регулирования и управления. –
М.: Наука, 1978.
3. Солодовников В.В. и др. Основы теории и элементы систем автоматического регули-
рования. – М.: Машиностроение, 1985. – 536 с.
4. Андриевских Б.Р., Фрадков А.Л. Избранные главы теории автоматического управле-
ния с примерами на языке MATLAB. – С.-Пб.: Наука, 1999. – 467 с.
5. Попов Е.П. Теория нелинейных систем автоматического регулирования и управления.
Учебное пособие. – М.: Наука, 1988. – 256 с.
6. Справочник по теории автоматического управления./Под. ред. А.А. Красовского. –
М.: Наука, 1987. – 712 с.
7. Цыпкин Я.З. Теория релейных систем автоматического регулирования. – М.: Гос. изд.
технико-теоретической лит. – 456 с.
8. Кунцевич В.М., Чеховой Ю.Н. Нелинейные системы управления с частотно- и ши-
ротно-импульсной модуляцией. – Киев: Технiка, 1970. – 340 с.
9. Вентильные преобразователи переменной структуры./ В.Е. Тонкаль, В.С. Руденко,
В.Я. Жуйков и др.; отв. ред. Шидловский А.К.; АН УССР, Ин-т электродинамики. – Киев;
Наукова думка, 1989. – 336 с.

Приложение А.
Варианты заданий на лабораторную работу № 2
Вариант 1.
Пусть задан объект управления с помощью передаточной функции вида
()
()()
Ws
ss
=
++
10
1 5
. Пусть управляющее воздействие u
y
=5. Построить САУ обеспечивающую
длительность процесса регулирования 0,05 с и перерегулирование 5%.
Вариант 2.
Пусть задан объект управления с помощью передаточной функции вида
()
()( )
Ws
ss
=
++
50
110
. Пусть управляющее воздействие u
y
=3. Построить САУ обеспечиваю-
щую длительность процесса регулирования 0,1 с и перерегулирование 5%.
Вариант 3.
Пусть задан объект управления с помощью передаточной функции вида
()
()()
Ws
ss
=
++
50
56
. Пусть управляющее воздействие u
y
=3. Построить САУ обеспечивающую
длительность процесса регулирования 0,05 с и перерегулирование 1%.
Вариант 4.
Пусть задан объект управления с помощью передаточной функции вида
()
()()
Ws
ss
=
++
5
5 1
. Пусть управляющее воздействие u
y
=3. Построить САУ обеспечивающую
длительность процесса регулирования 0,05 с и перерегулирование 1%.
