Косчинский С. Л., Косчинская Е. В. Основы автоматики и систем автоматического управления
Подождите немного. Документ загружается.

(лась) в левой части комплексной полуплоскости на расстоянии не меньшем чем at
kp
≈ 3/ .
При этом действительному определяющему полюсу будет соответствовать апериодический
переходный процесс, а комплексно-сопряженной паре определяющих полюсов будет соот-
ветствовать колебательный процесс.
В случае если в системе переходный процесс носит колебательный характер, то в нем
имеется перерегулирование
σ
вида
()
σ
π
π
φ
≈=
−⋅
−
ee
a
b
tg
k
k
k
. (2.5)
Где tg(
φ
k
) = b
k
/a
k
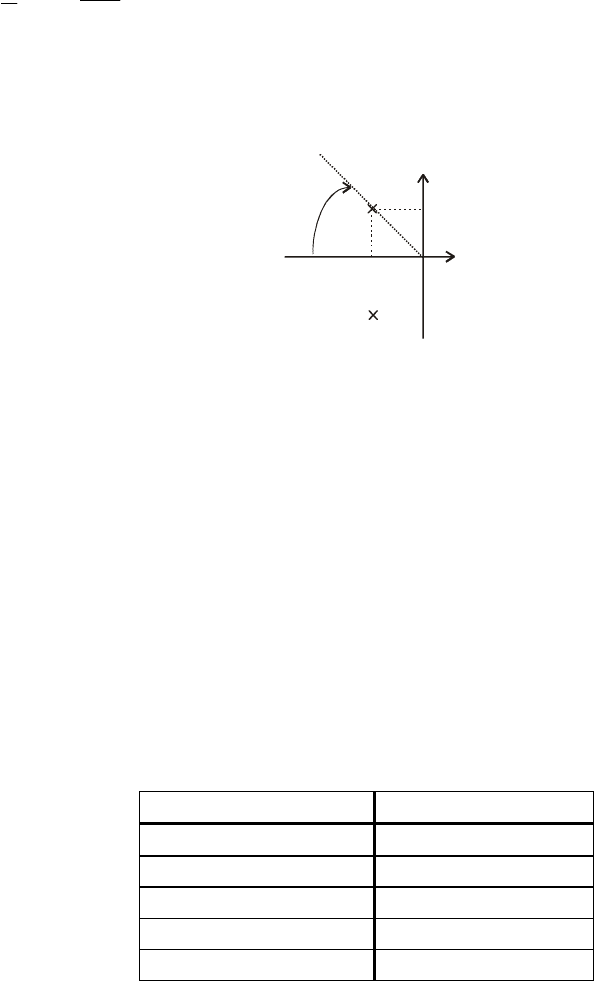
(рис. 2.1) и перерегулирование приведено в относительных единицах.
Im
Re
b
k
a
k
φ
k
Рис. 2.1. Сектор расположения полюсов по заданному перерегулированию
Соответственно, из рис. 2.1 видно, что величина перерегулирования полностью опреде-
ляется величиной угла
φ
k
. В табл. 2.1 приведены значения
φ
k
для различных перерегулирова-
ний σ.
Таблица 2.1
Значения f
k
для различных перерегулирований σ
σ
φ
k
0,5%
30,7°
1%
34,3°
5%
46°
10%
53°
30%
69°

Из всего вышеизложенного следует, что линейная САУ будет удовлетворять требовани-
ям к длительности переходного процесса и величине перерегулирования если все полюса ее
передаточной функции расположены в некотором сегменте (рис. 2.2).
Im
Re
a
k
φ
k
Рис. 2. Сегмент допустимого расположения полюсов передаточной функции САУ
из требований к длительности переходного процесса и к величине перерегулирования
Соответственно, задача синтеза линейной САУ может быть сформулирована, как обес-
печение расположения полюсов передаточной функции замкнутой САУ в некотором опреде-
ленном сегменте на комплексной плоскости. При этом стремятся, чтобы только один полюс
(или комплексно-сопряженная пара полюсов) располагались близко от мнимой оси. Осталь-
ные полюса стремятся максимально удалить от мнимой оси.
Метод модального управления.
Метод модального управления – аналитический метод синтеза линейных САУ. Указан-
ный метод обеспечивает заданное распределение полюсов передаточных функций замкнутой
САУ на комплексной плоскости. Естественно, возможность решения указанной задачи зави-
сит от степени наблюдаемости и управляемости САУ (строгие определения наблюдаемости и
управляемости выходят за рамки этого курса).
Постановка задачи. Пусть имеется ОУ, заданный в форме уравнений состояния.
dX
dt
AX Bu=+, (2.6)
где
nn
RA
,
∈
,
1,n
RB
∈
,
1,n
RX
∈
. Причем А и В удовлетворяют условию полной

управляемости (полная управляемость означает, что определитель, составленный из столб-
цов
()
det BAB A B
n
−
≠
1
0 . (2.7)
Требуется найти управление XCu
T
=
, где вектор управления
1,n
RC
∈
, должен быть
таким, чтобы все или часть собственных чисел (мод) матрицы
T
BCA
+
замкнутой САУ
имели заданные значения
Алгоритм метода модального управления состоит из следующих этапов:
1. Задаемся характеристическим полиномом замкнутой САУ (полином знаменателя).
Т.е. задаем желаемое расположение его корней
0)det()(
=−+=
EsBCASD
T
, Ds s s s
n
n
()
=+ ++ +
−
ααα
110
. (2.8)
2. Определяем характеристический полином разомкнутой САУ.
01
1
1
)det()( dSdSdSesASd
n
n
n
++++=−=
−
−
(2.9)
3. Из коэффициентов полиномов D(s) и d(s) сформируем вектор
[]
T
nn
ddl
1100
−−
−−=
αα
.(2.10)
4. Найдем искомый вектор управления
[]
[]
1
11
−
−−
⋅⋅−=
BAABBBABABlC
nnTT
,(2.11)
где A
ddd d
n
∪
−
=
−−− −
0 1 00
001 0
000 1
0 1 2 1
, B
∪
=
0
0
0
1
.
Пример синтеза линейной САУ.
Пусть задан объект управления с помощью передаточной функции вида

()
()()
Ws
ss
=
++
100
105
. Пусть управляющее воздействие u
y
=5. Построить САУ обеспечи-
вающую длительность процесса регулирования 0,1 с и перерегулирование 1%.
1. Преобразуем мат. описание будущей САУ к виду (2.6) (рис. 2.3). Для этого разобьем
передаточную функцию W(s) на простые сомножители. И приведем синтезируемую САУ к
виду на рис. 2.3.
() () ()
Ws W s W s
ss
=⋅=
+
⋅
+
1 2
100
10
1
5
W
1
W
2
x
1
x
2
u
y
ε
u
Рис. 2.3. Структурная схема синтезируемой САУ на начальном этапе синтеза
()
()
()
()
()( ) () ()( ) ()
xs
ss
xs
xs s
xs s s xs s xs
1 2
1
1 2 1
100
10
1
5
10 100 5
ε
ε
=
+
=
+
⋅+ = ⋅ ⋅+ =
,; , , или
dx
dt
x
dx
dt
xx uu
y
1
1
2
2 1
10 100 5
+⋅= ⋅ +⋅= = +
εε
,,, или
dx
dt
xu
dx
dt
xx
1
1
2
1 2
10 500 100
5
=− ⋅ + + ⋅
=−⋅
,
.
AB
=
−
−
=
100
1 5
100
0
,.
2. Находим управление u. Проверяем управляемость САУ det
100 1000
0 100
0
−
≠
, т.е. сис-
тема управляема.
Определяем сегментные ограничения на расположение полюсов замкнутой САУ. Из
требования к длительности переходного процесса a
k
=3/t
p
=3/0,1=30; из требования к перере-
гулированию по табл. 2.1 находим
φ
k доп
=34,3
°
.
Задаемся желаемым расположением полюсов замкнутой САУ в данном сегментном ог-
раничении. Пусть s
1
=-50+j10; s
2
=-50-j10 при этом
φ
k
=11,3
°
<34,3
°
. Тогда характеристический
полином замкнутой САУ будет иметь вид (s+50-j10)(s+50+j10)=(s+50)
2
+100=s
2
+100s+2600.
Характеристический полином разомкнутой САУ из условия задачи имеет вид
(s+10)(s+5)=s
2
+15s+50.
В соответствии с (2.10) составляем вектор l={2550, 85}
T
.
В соответствии с (2.11) определяем искомый вектор управления
ABABAB
∪∪∪∪
=
−−
=⋅=
−
⋅=
−
0 1
50 15
0
1
1
15
1000
100
,, ,
C
T
=− ⋅
−
⋅
−
=− −
−
2550 85
0 1
115
100 1000
0 100
085 21 25
1
,,.
Поскольку u=C
T
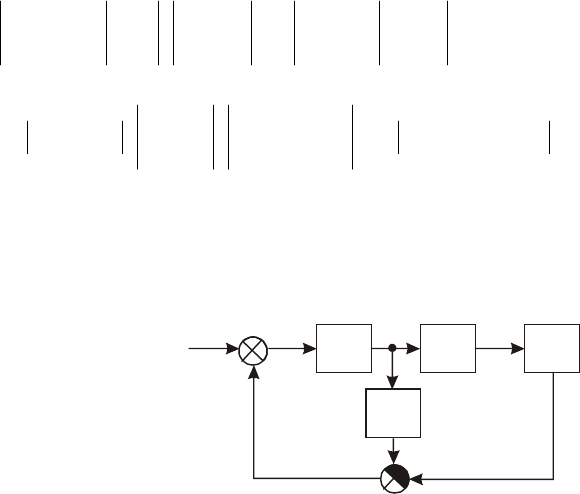
X, то окончательно структура синтезированной САУ приведена на
рис.2.4.
W
1
W
2
x
1
x
2
u
y
ε
u
0,85
21,25
Рис.2.4 Структурная схема синтезированной САУ
Характерно, что метод модального управления абсолютно не учитывает статические
свойства САУ. Поэтому зачастую необходимо проводить коррекцию статической ошибки
регулирования до применения метода модального управления. А после процедуры синтеза
необходимо осуществлять проверку статических свойств САУ.
2.3 Описание лабораторной работы.
1. Получить у преподавателя номер варианта синтезируемой САУ.
2. В соответствии с заданием синтезировать линейную САУ методом модального
управления.
3. С помощью программы Classic определить динамические и статические свойства
синтезированной САУ.
Варианты заданий на лабораторную работу приведены в Приложении А.
2.4 Контрольные вопросы.
1. Как изменится тип переходного процесса в Вашей системе, если выбрать в качестве
определяющего действительный полюс и если выбрать в качестве определяющих комплекс-
но-сопряженную пару полюсов?
2. Поясните алгоритм выбора сегментных ограничений на расположение полюсов пере-
даточной функции синтезируемой САУ?
3. В чем на Ваш взгляд принципиальной отличие структуры САУ синтезированной по
методу модального управления от структуры САУ синтезированной по методу последова-
тельной коррекции? Которую из этих структур проще реализовать в виде схемы электриче-
ской принципиальной? Поясните ответ.
4. Возможно ли синтезировать САУ методом модального управления не разбивая пере-
даточную функцию на простые сомножители? Можно ли синтезировать САУ методом мо-
дального управления выделяя в качестве одного из простых сомножителей постоянный ко-
эффициент K? Поясните ответ.
3 Лабораторная работа № 3 “Исследование релейных систем
автоматического регулирования”
3.1 Цель работы.
Получить практические навыки исследования и проектирования релейных САУ.
3.2 Краткие теоретические сведения.
Система автоматического управления называется релейной, если в качестве регулирую-
щего элемента в ней используется релейный элемент. Типовая структурная схема релейной
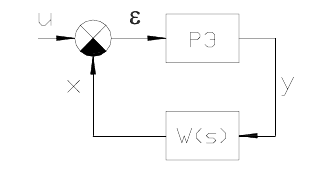
САУ представлена на рис. 3.1.
Рис. 3.1 Релейная САУ: РЭ – релейный элемент; ε – ошибка регулирования;
U – задающее воздействие (уставка); x –регулируемая величина.
Основные показатели качества релейной САУ определяются передаточной функцией
W(s) ее непрерывной части и характеристикой релейного элемента. Некоторые типовые ха-
рактеристики релейных элементов представлены на рис. 3.2.
Как видно из рис. 3.2, величина на выходе релейного элемента изменяется «скачком»
при переходе входной величиной некоторого порогового значения. При этом САУ реализует
так называемое дискретное регулирование (рис. 3.3). Т.е. включение релейного элемента
происходит при положительной ошибке регулирования, при этом регулируемая величина
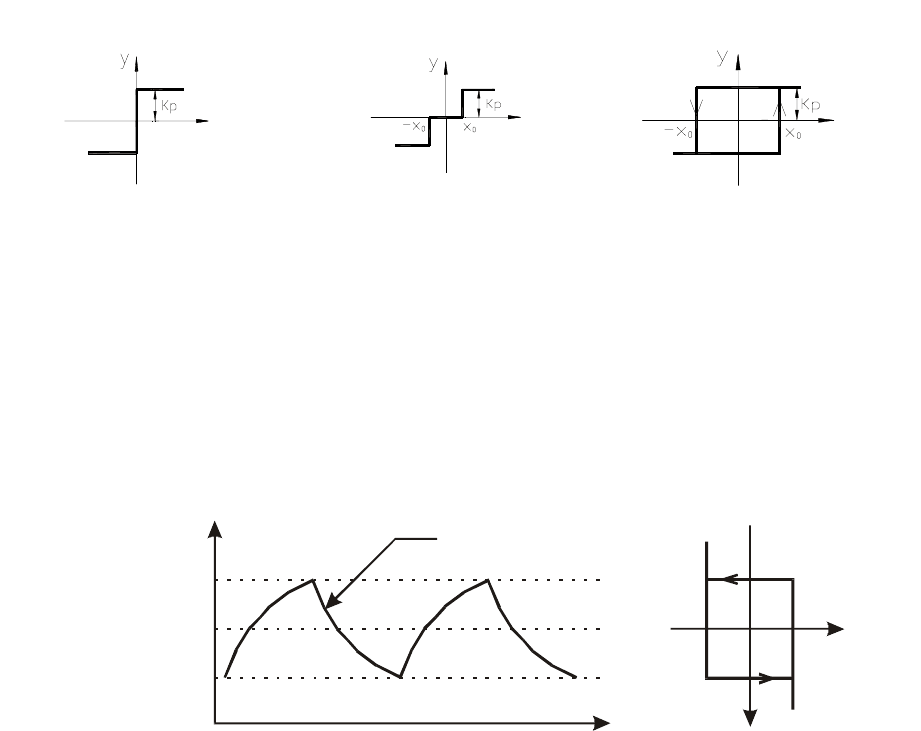
начинает возрастать, стремясь к значению управляющей величины. Соответственно, отклю-
чение релейного элемента происходит при нулевой (или отрицательной) ошибке регулиро-
вания. Как видно из рис. 3.3 величина гистерезиса релейного элемента определяет точность
регулирования в САУ.
ε
ε
ε
а) б) в)
Рис. 3.2 Типовые характеристики релейных элементов в составе САУ. а) «Идеальное
реле», б) релейный элемент с зоной нечувствительности, в) релейный элемент с пространст-
венным гистерезисом.
U
U-
χ
0
U+
χ
0
X(t)
t
y
ε
X(t)
Рис. 3.3 Процесс регулирования в релейной САУ.
3.3 Описание лабораторной работы.
1. Собрать лабораторную установку в соответствии с рис. 3.4. Данная установка пред-
ставляет собой релейную САУ регулирования температуры печи, в которой в качестве ис-
пользуется релейный элемент с пространственным гистерезисом. Схема электрическая
принципиальная установки приведена в приложении Б.
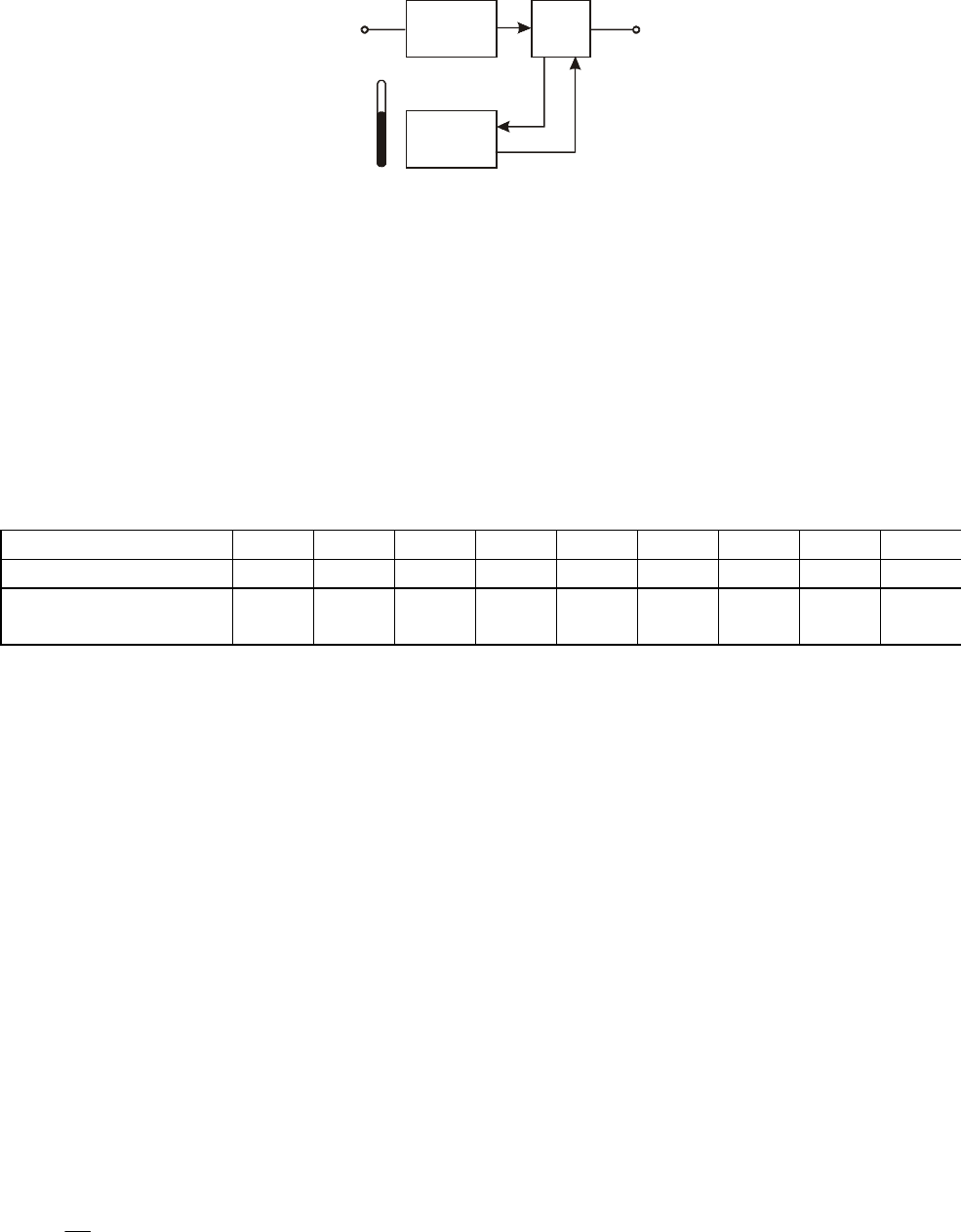
Блок
питания
САУ
печь
~220 B
~220 B
от
термопары
t
0
Рис. 3.4. Схема включения лабораторной установки.
2. Включить установку и измеряя значения времени и температуры печи заполнить
табл. 3.1
Таблица 3.1
Результаты измерений
время, мин
температура,
o
C
состояние релейного
элемента, вкл/откл
Измерения проводить до истечения трех-четырех переключений релейного элемента с
дискретой по времени 2 мин.
3. По данным табл. 3.1 построить график изменения температуры печи от времени в
САУ. Выделить на графике переходный и установившийся процессы. Определить по графи-
ку установившегося процесса максимальное и минимальное значения температуры печи;
значение управляющего воздействия u и величину гистерезиса релейного элемента χ
0
.
4. По полученным экспериментальным данным определить постоянную времени объек-
та управления - печи.
Будем полагать, что печь описывается линейной математической моделью вида
bax
dt
dx
+= , (3.1)

где x- регулируемая величина (температура печи), 1/a - постоянная времени печи, вели-
чина b зависит от состояния релейного элемента (b>0 при включенном релейном элементе и
b<0 при отключенном релейном элементе).
Решение уравнения (3.1) в общем виде
a
b
eetxtx
ttatta
)1()()(
)()(
0
00
−⋅−⋅
−−⋅= . (3.2)
Найдем постоянную времени печи (величину 1/a), определяющую инерционность печи.
Возьмем из таблицы три точки из интервала, на котором отсутствовали переключения
релейного элемента (т.е. релейный элемент был в одном и том же состоянии), например, рас-
смотрим значения времени t
1
=10 мин, t
2
=15 мин, и t
3
=20 мин. Тогда из (3.2), получим
a
b
eetxtx
tata
)1()()(
12
∆⋅∆⋅
−−⋅= ,
a
b
eetxtx
tata
)1()()(
23
∆⋅∆⋅
−−⋅= , (3.3)
где
∆
t=t
2
-t
1
=t
3
-t
2
=5 (мин) интервал времени между двумя рассматриваемыми отсчетами.
Из уравнений (3.3) выразим 1/a и получим постоянную времени печи.
3.4 Контрольные вопросы.
1. Как изменится переходный процесс в системе если в качестве регулятора использо-
вать "идеальное реле"? Каковы будут амплитуда и частота установившихся колебаний в сис-
теме? Ответ проиллюстрируйте рисунком.
2. Как изменится переходный процесс в системе если в качестве регулятора использо-
вать релейный элемент в временным гистерезисом? Каковы будет амплитуда и частота уста-
новившихся колебаний в системе? Используйте модель (3.1) и получите соотв. выражения.
3. Определите, использую модель (3.1) до какого значения температуры нагреется печь,
если отключить релейный регулятор и подать питание непосредственно на печь.
