Koren B., Vuik K. (Editors) Advanced Computational Methods in Science and Engineering

Подождите немного. Документ загружается.

Gang Wang, Chris R. Kleijn, and Marc-Olivier Coppens

1 Introduction

PDEs (Partial Differential Equations) emerge as governing equations in diverse dis-

ciplines of science and engineering. PDE-based optimization problems are often

encountered in the context of optimal design, optimal control and parameter estima-

tion, and are computationally challenging because of the size and complexity of the

discretized PDEs [1]. The solution of the PDEs is often the most time-consuming

procedure for PDE-based optimizations. Therefore, rather than gradient-free opti-

mization methods (e.g., genetic algorithms), gradient-based optimization methods

are typically selected. This minimizes the need to evaluate the objective function

and, consequently, the need to actually solve the PDEs. For the solution of PDE-

based optimization problems, one can make use of existing, sophisticated PDE

solvers and optimization packages. Biegler et al. [1] presented an excellent overview

on the issues that need to be addressed for PDE-based optimizations.

The reduced gradient method is an ideal candidate for PDE-based optimization

problems, since it employs gradient information to reduce the need for the evalu-

ation of the objective function, and could be implemented with existing software.

More importantly, the implementation could be tailored to different PDE-based op-

timization problems by an appropriate choice of existing software. However, this

advantage of the reduced gradient method has not been addressed well, even though

the reduced gradient method has been used to solve PDE-based optimization prob-

lems that arise from the optimal operation of a chemical vapor deposition (CVD)

reactor [2], dynamic optimization of dissipative PDE systems [3], inverse parame-

ter estimation [4] and optimal control of steady incompressible Navier-Stokes ﬂows

[5].

The objective of this paper is to discuss the implementation of the reduced gradi-

ent method for a PDE-based optimization problem on the basis of existing software.

As a showcase, the reduced gradient method is implemented using a multigrid PDE

solver, MGD9V [6], and a gradient-based optimization package, NLPQL [7], to

solve a model problem that arises from the optimal design of hierarchically struc-

tured porous catalysts. The method discussed in this book chapter was presented in

[8], whereas results of the application to structured porous catalysts were presented

in more details in [9].

2 Implementation framework

To introduce the implementation framework, consider the following generic formu-

lation of nonlinear programming

min f

(x), (1a)

s. t. g

(x) ≤ 0. (1b)

438

Multi-Scale PDE-Based Design of Hierarchically Structured Porous Catalysts

where f

: R

→ R and g

: R

→ R

are continuously differentiable functions.

Equation (1a) is the objective function, and Eq. (1b) the constraint. x ∈ R

is the

optimization variable vector.

The problem consisting of Eqs. (1a-b) could be readily solved using a num-

ber of gradient-based optimization packages, e.g., SNOPT [10], MINOS [11],

LANCELOT [12], DONLP2 [13] and GRG2 [14]. To do so, all a user needs to do is

to provide the information required by the optimization package. The standard input

information includes the value and gradient of the objective function, Eq. (1a), and

the Jacobian matrix and value of the constraints, Eq. (1b). To illustrate how to obtain

this input information, consider the following PDE-based optimization problem

min f

) f

[q(x

),x

], (2a)

s. t. g

) ≤ 0, (2b)

where f

: R

→ R and g

: R

→ R

are continuously differentiable functions.

Equation (2a) is the objective function. x

= q(x

) is mathematically equivalent to

the discretized equations h(x

) = 0, which result from the discretization of a

PDE in terms of ﬁnite element or ﬁnite difference methods. x

∈ R

and x

∈ R

are state variable and design variable vectors, respectively. State variables are those

that could be determined by solving h(x

) = 0, with given data, i.e., geometry,

coefﬁcients, boundary conditions and initial conditions. These data are the design

variables.

For the problem consisting of Eqs. (2a-b), the objective function could be evalu-

ated by solving the discretized equations h(x

) = 0. A numerical solver could be

used to carry out these calculations. The Jacobian matrix and value of the non-PDE

constraint, Eq. (2b), are easily obtained as follows. To compute the gradient of the

objective function, differentiate Eq. (2a):

d f

∂ f

∂ x

∂ f

∂ x

, (3)

∂ f

∂ x



∂ f

∂ x

∂ f

∂ x

···

∂ f

∂ x



, (4a)

∂ f

∂ x



∂ f

∂ x

∂ f

∂ x

···

∂ f

∂ x



, (4b)

∂ x







∂ x

···

∂ x

···

∂ x







. (4c)

439

Gang Wang, Chris R. Kleijn, and Marc-Olivier Coppens

Typically, Eqs. (4a-b) are easily evaluated either analytically or by numerical differ-

entiation. To compute Eq. (4c), differentiate both sides of the discretized equations,

h(x

) = 0:

∂ h

∂ x

∂ h

∂ x

= 0, (5)

where

∂ h

∂ x







∂ h

∂ x

∂ h

∂ x

···

∂ h

∂ x

∂ h

∂ x

∂ h

∂ x

···

∂ h

∂ x

∂ h

∂ x

∂ h

∂ x

···

∂ h

∂ x







, (6a)

∂ h

∂ x







∂ h

∂ x

∂ h

∂ x

···

∂ h

∂ x

∂ h

∂ x

∂ h

∂ x

···

∂ h

∂ x

∂ h

∂ x

∂ h

∂ x

···

∂ h

∂ x







. (6b)

Equations. (6a-b) can be evaluated either analytically or by numerical differentia-

tion. From Eq. (5),

∂ x

= −

∂ h

∂ x



∂ h

∂ x



−1

. (7)

Substitute Eq. (7) into Eq. (3):

d f

∂ f

∂ x

−

∂ h

∂ x



∂ h

∂ x



−1

∂ f

∂ x

. (8)

For numerical efﬁciency, the inverse of the matrix, Eq. (6b), is not evaluated directly,

but calculated by solving the linear equation



∂ h

∂ x



z =

∂ f

∂ x

. (9)

Note that the coefﬁcient matrix of the linear equation (9) is a Jacobian matrix of the

discretized equations h(x

) = 0. Substituting z ∈R

into Eq. (8), we get:

d f

∂ f

∂ x

−

∂ h

∂ x

z. (10)

440

Multi-Scale PDE-Based Design of Hierarchically Structured Porous Catalysts

At this point, one could provide all the information that a gradient-based optimiza-

tion package needs to solve the problem consisting of Eqs. (2a-b). The gradient, Eq.

(10), is the so-called reduced gradient, therefore the implementation strategy con-

structed here is called the reduced gradient method [15]. According to the above

discussion, the reduced gradient method could be readily implemented on the basis

of existing software to solve a PDE-based optimization problem. Furthermore, in

this implementation framework, the software can be freely chosen among those that

can perform the aforementioned calculations. This feature can be employed to tailor

the implementation to different problems. It should be mentioned that the reduced

gradient can be calculated either by Eqs. (9-10) or by numerical differentiation. The

fact that both methods should yield the same value for the reduced gradient can be

employed in debugging the code.

3 PDE-based design of hierarchically structured porous catalysts

In this section, the above strategy is applied to solve the model problem that arises

from the optimal design of hierarchically structured porous catalysts. Catalysts are

essential for the fast and selective chemical transformation of raw materials to prod-

ucts, for instance, crude oil to gasoline, diesel and plastics. Discovery of more ef-

ﬁcient catalysts therefore has a large economical impact. Note that, among the top

ten in the Fortune Global 500, six are chemical companies [16]. Discovery of more

efﬁcient catalysts also helps to protect the environment, since catalysts are used in

emission control and waste water treatment. It also contributes to saving energy and

resources and, consequently, building a sustainable future.

One way to design more efﬁcient catalysts is to structure the catalysts in a rational

way. The idea is the following: catalysts are usually nanoporous materials, or they

are formed by the dispersion of nanoparticles over the internal surface of nanoporous

materials. These nanoporous materials often have an extremely large internal surface

area, which is beneﬁcial because catalytic reactions occur on the surface. Note that

the internal surface area of one gram of nanoporous catalyst could be as large as the

area of ﬁve tennis courts! However, this huge internal surface could be inaccessible,

limiting the efﬁcient use of the catalytic materials, since molecular transport in the

nanopores is substantially slower than that in the bulk, and the nanopores are easy to

block. This indicates that, apart from the nanopores where reactions actually occur,

a ”distribution” network of large pores is needed for the catalyst, just like a road

network is needed for a city. One important question is how to design this distribu-

tion network for optimal catalyst performance. PDE-based optimizations were used

to study this question [9,17-19]. Note that the PDE-based optimization is a multi-

scale problem because of two reasons: (1) there is a network of narrow nanopores

that are part of a porous matrix (treated as a continuum in the paper, as is justiﬁed

by earlier research); (2) the size of the large pores is allowed to span a few orders

of magnitude in the optimizations, even if it could eventually turn out that a broad

distribution of large pore diameters is not the optimal solution.

441

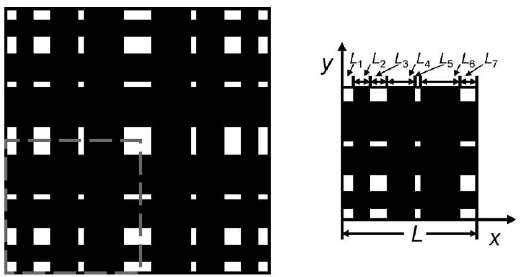
Gang Wang, Chris R. Kleijn, and Marc-Olivier Coppens

Fig. 1 Hierarchically structured porous catalyst with 2N ×2N large pores (left) and its bottom-left

quarter (right). N = 3 for illustration only. The nanoporous, catalytically active material (where the

nanopores are not shown explicitly) is indicated in white, the large pores in black.

Gheorghiu and Coppens [17] optimized a model for the studied structured

porous catalyst, shown in Figure 1. For reasons of computational simplicity, a two-

dimensional square geometry was used, without affecting the generality of the con-

clusions [9, 17-19]. The square hierarchical pore structure is a nanoporous catalyt-

ically active material, in which 2N ×2N large pores have been introduced. N is an

arbitrary positive integer, typically 1 −100. It was assumed that the large pores are

straight, perpendicular to the square sides, and have a constant diameter as they go

through the entire square. Four-fold symmetry was imposed, as the optimum was

assumed to have this symmetry. Therefore, only the bottom-left quarter of the en-

tire catalyst (as shown in the right part of Figure 1) was modelled. The aim was

to maximize the normalized catalytic yield η with respect to the design variables

(i = 1,2, ··· ,2N + 1) as labelled in the right part of Figure 1:

max η =

Ω

k cdx dy /(k c

), (11a)

s. t.

2N+1

∑

i=1

= L, (11b)

> 0 i = 1,2, ··· ,2N + 1, (11c)

where Ω is the area occupied by the nanoporous material, k the intrinsic rate con-

stant, c the concentration and c

the (ﬁxed) concentration on the external surface of

the catalyst; L is half of the catalyst size as labelled in the right part of Figure 1.

Equations (11b-c) are algebraic (non-PDE) constraints.

The equations governing steady-state diffusion and ﬁrst-order reaction in the

bottom-left quarter of the catalyst are

442

Multi-Scale PDE-Based Design of Hierarchically Structured Porous Catalysts

∂

∂ x



∂ c

∂ x



∂

∂ y



∂ c

∂ y



= 0 in the large pores (black), (12a)

∂

∂ x



∂ c

∂ x



∂

∂ y



∂ c

∂ y



= kc in the nanoporous material (white), (12b)

with the boundary conditions

x = 0 : c = c

, (13a)

y = 0 : c = c

, (13b)

x = L :

∂ c

∂ x

= 0, (13c)

y = L :

∂ c

∂ y

= 0, (13d)

where D

is the molecular diffusion coefﬁcient in the large pores, and D

is the

effective diffusion coefﬁcient in the nanoporous material. D

is typically 10

−

Equations (11-13) can be made dimensionless, as follows:

max η =

Ω

¯cd ¯x d ¯y, (14a)

s. t.

2N+1

∑

i=1

= 1, (14b)

> 0 i = 1,2, ··· ,2N + 1, (14c)

and

∂

¯c

∂ ¯x

∂

¯c

∂ ¯y

= 0, in the large pores, (15a)

∂

∂ ¯x



∂ ¯c

∂ ¯x



∂

∂ ¯y



∂ ¯c

∂ ¯y



= Φ

¯c, in the nanoporous material, (15b)

with the boundary conditions

¯x = 0 : ¯c = 1, (16a)

¯y = 0 : ¯c = 1, (16b)

¯x = 1 :

∂ ¯c

∂ ¯x

= 0, (16c)

¯y = 1 :

∂ ¯c

∂ ¯y

= 0, (16d)

where

443

Gang Wang, Chris R. Kleijn, and Marc-Olivier Coppens

= L

, (17a)

β =

, (17b)

¯c =

(17c)

¯x =

, (17d)

¯y =

, (17e)

, i = 1,2, ··· ,2N + 1. (17f)

Gheorghiu and Coppens [17] employed a genetic algorithm to solve the above

PDE-based optimization problem. The solution of the PDE needed by the genetic

algorithm was obtained using FEMLAB. This numerical scheme is easy to imple-

ment, but suffers from low efﬁciency, because the genetic algorithm requires many

more solutions of the PDE than a gradient-based method. To avoid these problems,

the reduced gradient method is implemented on the basis of the specialized PDE

solver, MGD9V [6], and the gradient-based optimization package, NLPQL [7]. Note

that the use of FEMLAB does not imply the use of a derivative-free optimization

algorithm, e.g, a genetic algorithm [20].

Fig. 2 Illustration of computational cells. The nanoporous, catalytically active material (where the

nanopores are not shown explicitly) is indicated in white, the large pores in black.

444

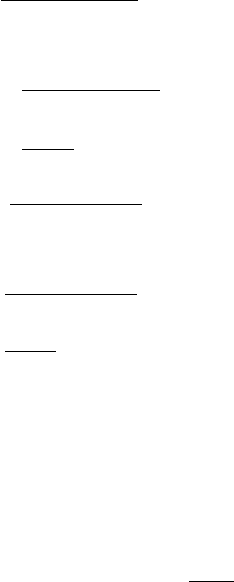
Multi-Scale PDE-Based Design of Hierarchically Structured Porous Catalysts

As shown in Figure 2, the diffusion-reaction equation, Eqs. (15a-b), is discretized

in terms of the ﬁnite volume method on a matrix of computational cells [21]. The

computational cells have nearly the same size, and none of the cells crosses the

interfaces between the large pores and the nanoporous material. For the cell (i, j)

(the cell in the ith column counting from the left and the jth row counting from the

bottom), the discretized equation is

i j



i j,right

−F

i j,le f t





i j,top

−F

i j,botten



−R

i j

= 0, (18)

where R

i j

is the dimensionless reaction rate in the cell (i, j). F

i j,top

, F

i j,bottom

i j,right

and F

i j,le f t

are the dimensionless ﬂuxes through the four sides of the cell (i, j):

i j

(

¯c

i j

∆ ¯x

, when the cell (i,j) is inside the nanoporous material,

0, when the cell (i,j) is inside the large pores,

(19a)

i j,top











¯c

i, j+1

− ¯c

i, j

(∆ ¯x

+ ∆ ¯x

j+1

)/2

∆ ¯x

, j = 1,2, ··· ,n

−1,

0, j = n

(boundary on the top),

(19b)

i j,bottom











¯c

i, j

− ¯c

i, j−1

(∆ ¯x

+ ∆ ¯x

j−1

)/2

∆ ¯x

, j = 2,3, ··· ,n

¯c

i j

−1

∆ ¯x

, j = 1 (boundary on the bottom),

(19c)

i j,right











¯c

i+1, j

− ¯c

i, j

(∆ ¯x

i+1

+ ∆ ¯x

)/2

∆ ¯x

, i = 1, 2,··· , n

−1,

0, j = n

(boundary on the right),

(19d)

i j,le f t











¯c

i, j

− ¯c

i−1, j

(∆ ¯x

+ ∆ ¯x

i−1

)/2

∆ ¯x

, i = 2, 3,··· , n

¯c

i j

−1

∆ ¯x

, i = 1 (boundary on the left),

(19e)

where ¯c

i j

is the concentration in the center of the cell (i,j). ∆ ¯x

is the length of the

cell (i,j) in the horizontal direction. Note that, as a result of the four-fold symmetry,

∆ ¯x

is also the length of the cell (j,i) in the vertical direction. n

is the number of the

cells in a row or a column.

When the ﬂux passes the interface between the large pores and the nanoporous

material, the dimensionless diffusivity, α, is determined from [22]

α =

2β

β + 1

. (20a)

Otherwise, α is determined from

445

Gang Wang, Chris R. Kleijn, and Marc-Olivier Coppens

α =

(

β, when the cell (i,j) is inside the nanoporous material.

1, when the cell (i,j) is inside the large pores.

(20b)

A system of discretized equations, which is equivalent to h(x

) = 0 in Section

2, is obtained by assembly of Eq. (18) for all the cells. There are many existing

solvers for the discretized equations. The multigrid solver, MGD9V, is selected here

because of two reasons. (1) A multigrid algorithm has proven to be the most efﬁ-

cient method for the equations that result from the discretization of elliptic PDEs

[23]. (2) This multigrid solver is specially designed to deal with numerical difﬁ-

culties that arise from the discontinuous diffusion coefﬁcient across the interface.

However, MGD9V might break down for some reason. To handle this exception,

an ICCG (Incomplete Cholesky Conjugate Gradient) was implemented to solve the

linear equations when MGD9V fails [24]. Note that an algebraic multigrid method

might be employed to avoid the need to use the slow ICCG as a safeguard [25].

However, our implementation is sufﬁciently efﬁcient for the application considered

here. Furthermore, ICCG is robust and it is readily implemented. While MGD9V

as a black-box solver is easy to use, its source code can be acquired free. This is

desirable for the integration of all the codes.

The discretized equations are linear with respect to the state variables (concen-

trations) and, therefore, the Jacobian matrix of the discretized equations, which is

equivalent to

∂ h

∂ x

in Section 2, is the same as the coefﬁcient matrix of the discretized

equations. As a result, ICCG-safeguarded MGD9V is also used for the solution of

the linear equations that are equivalent to Eq. (9) in Section 2.

∂ H

i j

∂

is evaluated

using the chain rule to obtain the matrix that is equivalent to

∂ h

∂ x

in Section 2:

∂ H

i j

∂

∑

l=1

∂ H

i j

∂ ∆ ¯x

∂

, (21)

where

∂ H

i j

∂ ∆ ¯x

is easy to obtain from Eqs. (19-20).

From straightforward geometrical consideration,

is the sum of a subset of

∆ ¯x

(l = 1, ··· ,n

), as shown in Figure 2. Therefore,

∂ ∆ ¯x

∂

is equal to unity if ∆ ¯x

belongs to that subset and is equal to zero if not. The discretized objective function

can be expressed either as the sum of the reaction rates over all the cells or as the sum

of the ﬂuxes through the boundary. The two expressions are equivalent, which could

be shown by adding Eq. (18) over all the cells. The discretized objective function,

expressed as the sum of the ﬂuxes through the boundary, is the following:

η =

∑

j=1

j,right

∑

i=1

,top

−

∑

j=1

1 j,le f t

−

∑

i=1

i1,bottom

. (22)

446

Multi-Scale PDE-Based Design of Hierarchically Structured Porous Catalysts

Since there is no ﬂux through the top and right boundaries, so that, combined with

Eqs. (19c) and (19e):

η =

∆ ¯x

∑

j=1

α(1 − ¯c

1 j

)∆ ¯x

. (23)

Therefore,

∂ η

∂ ¯c

i j







0 i 6= 1.

−4α

∆ ¯x

i = 1.

(24)

Note that

∂ η

∂ ¯c

i j

is equivalent to

∂ f

∂ x

in Section 2.

∂ η

∂

, which is equivalent to

∂ f

∂ x

in Section 2, is calculated (using the chain rule) from

∂ η

∂

∑

j=1

∂ η

∂ ∆ ¯x

∂

, (25)

where

∂ ∆ ¯x

∂

is computed in the same way as discussed above and

∂ η

∂ ∆ ¯x











−

(∆ ¯x

)

∑

k=2

α(1 − ¯c

)∆ ¯x

, j = 1.

4α(1 − ¯c

1 j

)

∆ ¯x

, j 6= 1.

(26)

Table 1 Summary of the numerical experiments (Φ

= 1, β = 0.01): (a) number of com-

putational cells. (b) number of optimization variables. (c) number of evaluations of objec-

tive function. (d) number of evaluations of reduced gradient. (e) number of calls for linear

solvers. (f) number of calls for ICCG (g) number of iterations (h) CPU time (seconds) (i) optimal

value.

Case 1 Case 2 Case 3 Case 4 Case 5 Case 6 Case 7

(a) 129 × 129 257× 257 257× 257 257 × 257 513× 513 513× 513 513× 513

(b) 101 101 161 201 101 161 201

(d) 12 11 12 10 12 11 9

(e) 50 44 50 41 49 44 36

(f) 6 4 8 7 8 6 6

(g) 12 11 12 10 12 11 9

(h) 2.52 13.86 21.39 19.59 211.52 174.28 166.86

(i) 0.52010 0.52030 0.52078 0.52097 0.52040 0.52090 0.52101

At this point, all the ingredients that are needed to implement the framework

established in Section 2 are available for this particular PDE-based optimization

problem. A Fortran program was developed by combining NLPQL, MGD9V and a

limited amount of in-house coding, in the way described in the framework. All the

447