Koren B., Vuik K. (Editors) Advanced Computational Methods in Science and Engineering

Подождите немного. Документ загружается.

G.S. Stelling and M. Zijlema

0 5 10 15 20 25 30

−0.8

−0.6

−0.4

−0.2

0.2

x [m]

z [m]

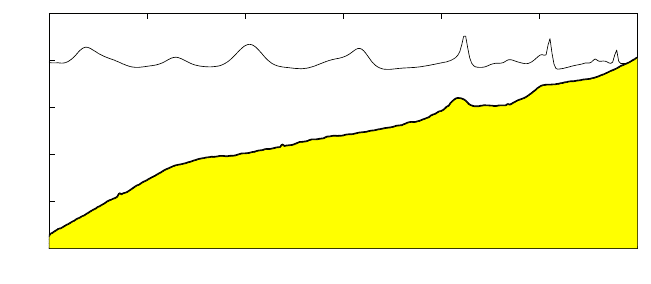
Fig. 11 A snapshot of the free surface and bathymetry of the laboratory ﬂume experiment of Boers

[4].

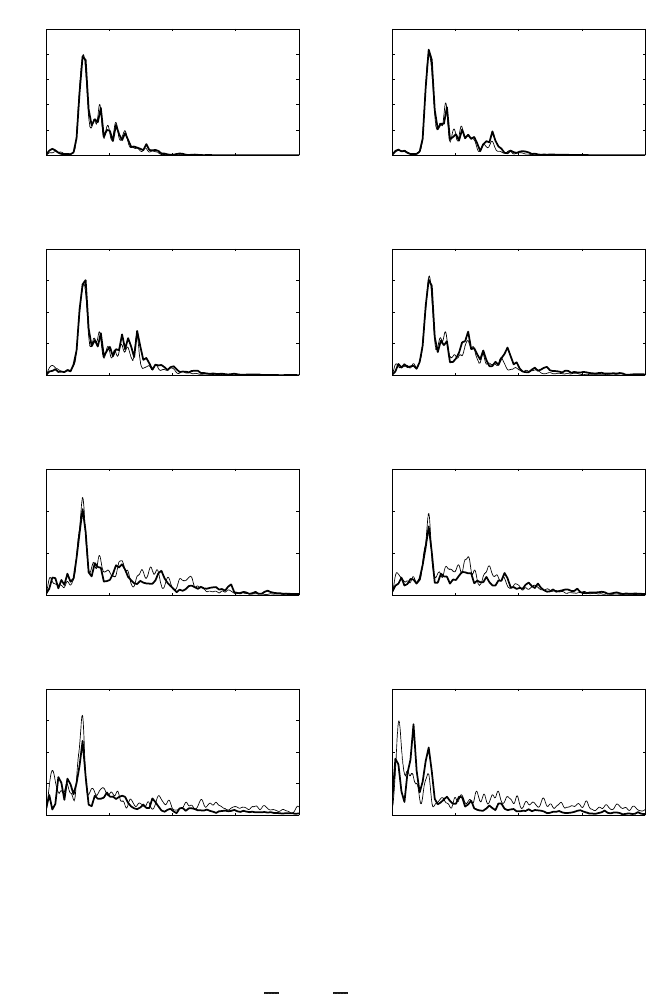
tion of wave energy through the ﬂume where the amount of energy in the short

waves reduces, whereas the amount of energy in the long waves increases. Note the

slight overestimation of the energy density in the low-frequency part at x =26m

and x =28m, which might be due to the reﬂection of infragravity waves against the

offshore boundary.

4.5 Deformation of waves by an elliptic shoal on sloped bottom

Deformation of waves by a shoal on plane sloping bed is very interesting because

of practical importance in the context of surf zone dynamics. From a physical point

of view, this wave transformation is challenging, because the waves are undergoing

shoaling, refraction, diffraction and nonlinear dispersion. The experiment conducted

by Berkhoff et al. [3] has served as a standard test case for verifying several numer-

ical wave models [11].

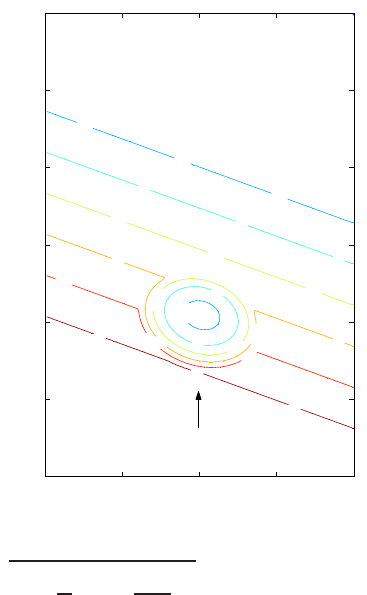
The simulations are considered in a rectangular basin [(x, y) : − 10 ≤x≤10,−10 ≤

y ≤ 20] with a plane slope of 1/50 on which an elliptic shoal is rested; see Fig. 13.

Let (x

′

) be the slope-oriented coordinates which are related to the (x,y) coordi-

nate system by means of a rotation over −20

. The still water depth without shoal

is given in meters by

H =







0.45, for y

′

< −5.484.

max(0.10, 0.45 −(5.484 + y

′

)/50), for y

′

≥ −5.484.

(49)

Instead of shoreline boundary, a minimum depth of 10cm is employed to prevent

breaking waves. The boundary of the shoal is given by

396

Numerical Modeling of Wave Propagation, Breaking and Run-Up on a Beach

0 0.5 1 1.5 2

x 10

−3

x = 5 m

E [m

/Hz]

0 0.5 1 1.5 2

x 10

−3

x = 10 m

0 0.5 1 1.5 2

x 10

−3

x = 16 m

E [m

/Hz]

0 0.5 1 1.5 2

x 10

−3

x = 20 m

0 0.5 1 1.5 2

x 10

−3

x = 22 m

E [m

/Hz]

0 0.5 1 1.5 2

x 10

−3

x = 24 m

0 0.5 1 1.5 2

0.5

1.5

x 10

−3

x = 26 m

f [Hz]

E [m

/Hz]

0 0.5 1 1.5 2

0.5

x 10

−3

x = 28 m

f [Hz]

Fig. 12 Computed (thin line) and measured (thick line) energy density spectra at different stations

for the irregular wave over bar-trough proﬁle. All spectra use equally spaced frequency intervals

and are ﬁltered.



′





′



= 1, (50)

whereas the thickness of the shoal is

397

G.S. Stelling and M. Zijlema

Fig. 13 Bathymetry corre-

sponding to the experiment of

Berkhoff et al. [3].

−10 −5 0 5 10

−10

−5

x [m]

y [m]

0.15

0.2

0.25

0.3

0.35

0.4

incident wave

d = −0.3 + 0.5

1 −



′



−



′

3.75



. (51)

Monochromatic waves with wave height of 4.64cm and wave period of 1.0s

are generated at lower boundary y = −10m. The upper boundary, y = 20m, is of

the outﬂow type where Sommerfeld radiation condition (7) is applied. The left and

right boundaries are insulated and the free-slip conditions are imposed.

For the present model, the grid size in both directions is set to 0.05m. The time

step is taken as 0.01s and the simulation period is set to 30s, so that a steady-state is

reached (

= 1 is taken). Since kH ≈1.9 in front of the domain, which is relatively

large, only computation with two equidistant layers is carried out.

To get an impression, the computation was carried out on a 64-bit AMD proces-

sor (1.8 GHz, 4MB L2 cache) with 4GByte internal memory. Code compilation is

achieved using Intel Fortran90 compiler 9.1 with the default optimization. The total

CPU time per grid point per time step required was about 20µs.

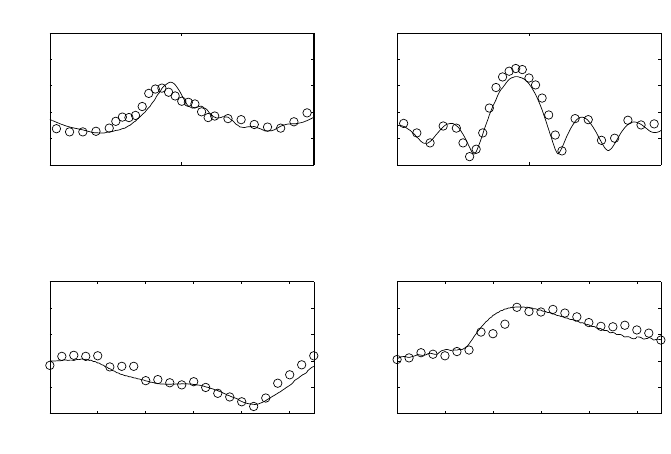
Proﬁles of the computed normalized wave height along four transects, which are

the most compelling ones, are given in Fig. 14 and compared with the experimental

data. The variation of the waves in cross direction representing the effects of com-

bined refraction and diffraction is predicted fairly well as shown by the comparison

of the computed and measured proﬁles along sections 2 and 5. The comparison

398

Numerical Modeling of Wave Propagation, Breaking and Run-Up on a Beach

−5 0 5

0.5

1.5

2.5

section 2 (y = 3m)

x [m]

relative wave height

−5 0 5

0.5

1.5

2.5

section 5 (y = 9m)

x [m]

relative wave height

0 2 4 6 8 10

0.5

1.5

2.5

section 6 (x = 2m)

y [m]

relative wave height

0 2 4 6 8 10

0.5

1.5

2.5

section 7 (x = 0m)

y [m]

relative wave height

Fig. 14 Computed and measured relative wave heights along different transects for the wave over

elliptic shoal. Present method (solid line), experiment (circles).

along sections 6 and 7 indicates that both shoaling and focussing of waves are very

well predicted by the present model.

5 Conclusions

A computational method for calculating the conventional nonlinear shallow water

equations, including non-hydrostatic pressure has been presented. For accuracy rea-

sons, the pressure is split-up into hydrostatic and non-hydrostatic parts. In the model

presented, the water depth is divided into a number of terrain-following layers and

the governing equations are integrated in each layer. Next, the second order com-

pact scheme is applied that enables to approximate short wave dynamics with a

very limited number of vertical grid points. Simple (semi-)implicit second order

ﬁnite differences are employed and are based upon a classical staggered grid. In

addition, advection terms in the momentum equations are approximated such as to

fulﬁl a proper momentum conservation, which is crucial for accurate computation

of energy losses in a wave breaking process. Initiation and cessation of breaking

waves can be described adequately by this method. This model does not require

any sort of tunable or empirical parameters. Semi-implicit time stepping is done

in combination with projection methods, where correction to the velocity ﬁelds for

the change in both surface elevation and non-hydrostatic pressure is incorporated.

399

G.S. Stelling and M. Zijlema

Finally, the algorithm utilizes a simple and numerically stable procedure yielding

non-negative water depths with which an accurate representation of the shoreline

motion is obtained.

The present method has been employed to model the main features of surf zone

dynamics, such as nonlinear shoaling, breaking of waves and wave run-up with

good agreement between predictions and observations. The model can be applied in

practical applications that comprise areas with spatial dimensions of the order of 10

to 100 wave lengths, particularly in the vicinity of the coast. In the near future, the

model will be coupled to a spectral wave model that can be applied on a scale of the

order of 100−1000 wave lengths.

References

1. A. Balzano. Evaluation of methods for numerical simulation of wetting and drying in shallow

water ﬂow models. Coast. Eng., 34: 83–107, 1998.

2. S. Beji and J.A. Battjes. Experimental investigation of wave propagation over a bar. Coast.

Eng., 19: 151–162, 1993.

3. J.C.W. Berkhoff, N. Booy, and A.C. Radder. Veriﬁcation of numerical wave propagation mod-

els for simple harmonic linear water waves. Coast. Eng., 6: 255–279, 1982.

4. M. Boers. Simulation of a surf zone with a barred beach; Part 1: wave heights and wave

breaking. Report no. 96-5, Communication on Hydraulic and Geotechnical Engineering, Delft

University of Technology, Delft, 1996.

5. M. Brocchini and D.H. Peregrine. Integral ﬂow properties of the swash zone and averaging. J.

Fluid Mech., 317: 241–273, 1996.

6. M. Brocchini, R. Bernetti, A. Mancinelli, and G. Albertini. An efﬁcient solver for nearshore

ﬂows based on the WAF method. Coast. Eng., 43: 105–129, 2001.

7. M. Brocchini, I.A. Svendsen, R.S. Prasad, and G. Bellotti. A comparison of two different types

of shoreline boundary conditions. Comput. Meth. Appl. Mech. Engng., 191: 4475–4496, 2002.

8. G.F. Carrier and H.P. Greenspan. Water waves of ﬁnite amplitude on a sloping beach. J. Fluid

Mech., 4: 97–109, 1958.

9. V. Casulli and G.S. Stelling. Numerical simulation of 3D quasi-hydrostatic, free-surface ﬂows.

J. Hydr. Eng. ASCE, 124: 678–686, 1998.

10. M.W. Dingemans. Comparison of computations with Boussinesq-like models and laboratory

measurements. MAST G8-M, Report H1684.12, Delft Hydraulics, Delft, 1994.

11. M.W. Dingemans. Water wave propagation over uneven bottoms. World Scientiﬁc, Singapore,

1997.

12. C.J. Galvin. Breaker type classiﬁcation on three laboratory beaches. J. Geophys. Res., 73:

3651–3659, 1968.

13. I. Gustafsson. A class of ﬁrst order factorization methods. BIT, 18: 142–156, 1978.

14. J.B. Hansen and I.A. Svendsen. Regular waves in shoaling water: experimental data. Technical

report, ISVA series paper 21, Technical University of Denmark, Denmark, 1979.

15. F.H. Harlow and J.E. Welch. Numerical calculation of time-dependent viscous incompressible

ﬂow of ﬂuid with a free surface. Phys. of Fluids, 8: 2182–2189, 1965.

16. S. Hibberd and D.H. Peregrine. Surf and run-up on a beach: a uniform bore. J. Fluid Mech.,

95: 323–345, 1979.

17. C. Hirsch. Numerical computation of internal and external ﬂows. John Wiley and Sons, Chich-

ester, 1990.

18. C.W. Hirt and B.D. Nichols. Volume of ﬂuid (VOF) method for the dynamics of free bound-

aries. J. Comput. Phys., 39: 201–225, 1981.

400

Numerical Modeling of Wave Propagation, Breaking and Run-Up on a Beach

19. K. Hu, C.G. Mingham, and D.M. Causon. Numerical simulation of wave overtopping of

coastal structures using the non-linear shallow water equations. Coast. Eng., 41: 433–465,

2000.

20. M.E. Hubbard and N. Dodd. A 2D numerical model of wave run-up and overtopping. Coast.

Eng., 47: 1–26, 2002.

21. N. Kobayashi, A.K. Otta, and I. Roy. Wave reﬂection and run-up on rough slopes. J. Waterw.

Port Coast. Ocean Eng., 113: 282–298, 1987.

22. A. Mahadevan, J. Oliger, and R. Street. A nonhydrostatic mesoscale ocean model. Part II:

numerical implementation. J. Phys. Oceanogr., 26: 1881–1900, 1996.

23. J.A. Meijerink and H.A. Van der Vorst. An iterative solution method for linear systems of

which the coefﬁcient matrix is a symmetric M-matrix. Math. Comput., 31: 148–162, 1977.

24. D.H. Peregrine. Long waves on a beach. J. Fluid Mech., 27: 815–827, 1967.

25. R. Scardovelli and S. Zaleski. Direct numerical simulation of free-surface and interfacial ﬂow.

Annu. Rev. Fluid Mech., 31: 567–603, 1999.

26. P.K. Stansby and J.G. Zhou. Shallow-water ﬂow solver with non-hydrostatic pressure: 2D

vertical plane problems. Int. J. Numer. Meth. Fluids, 28: 514–563, 1998.

27. G.S. Stelling. On the construction of computational methods for shallow water ﬂow problems.

PhD thesis, Delft University of Technology, Delft, 1983.

28. G.S. Stelling and S.P.A. Duinmeijer. A staggered conservative scheme for every Froude num-

ber in rapidly varied shallow water ﬂows. Int. J. Numer. Meth. Fluids, 43: 1329–1354, 2003.

29. G. Stelling and M. Zijlema. An accurate and efﬁcient ﬁnite-difference algorithm for non-

hydrostatic free-surface ﬂow with application to wave propagation. Int. J. Numer. Meth. Fluids,

43: 1–23, 2003.

30. M. Sussman, P. Smereka and S. Osher. A level set approach for computing solutions to incom-

pressible two-phase ﬂow. J. Comput. Phys., 114: 146–159, 1994.

31. I.A. Svendsen and P.A. Madsen. A turbulent bore on a beach. J. Fluid Mech., 148: 73–96,

1984.

32. V.V. Titov and C.E. Synolakis. Modeling of breaking and nonbreaking long-wave evolution

and runup using VTCS-2. J. Waterw. Port Coast. Ocean Eng., 121: 308–316, 1995.

33. E.F. Toro. Shock-capturing methods for free-surface shallow ﬂows. John Wiley, New York,

2001.

34. H.A. Van der Vorst. Bi-CGSTAB: a fast and smoothly converging variant of Bi-CG for the

solution of nonsymmetric linear systems. SIAM J. Sci. Stat. Comput., 13: 631–644, 1992.

35. M. Zijlema and G.S. Stelling. Further experiences with computing non-hydrostatic free-

surface ﬂows involving water waves. Int. J. Numer. Meth. Fluids, 48: 169–197, 2005.

36. M. Zijlema and G.S. Stelling. Efﬁcient computation of surf zone waves using

the nonlinear shallow water equations with non-hydrostatic pressure Coast. Eng.,

doi:10.1016/j.coastaleng.2008.02.020, 2008.

401

Hybrid Navier-Stokes/DSMC Simulations of Gas

Flows with Rareﬁed-Continuum Transitions

G. Abbate, B.J. Thijsse, and C.R. Kleijn

1 Introduction

Numerical simulations are an important tool for the design and optimization of gas

ﬂow equipment in many areas of science and technology. Most gas ﬂows can be

simulated using the continuum transport equations (Navier-Stokes), which describe

the transport of mass, momentum and energy. These equations are based on the

hypothesis that the mean free path length

of the gas molecules is very small in

comparison to a characteristic dimension L of the ﬂow. This dimension can be ei-

ther a physical dimension, e.g. a pipe diameter, or a ﬂow dimension, e.g. the gradient

length scale

∂φ

∂

on which some ﬂow property

changes signiﬁcantly. The dimen-

sionless Knudsen number Kn can be used to describe this situation:

Kn =

. (1)

When Kn < 0.01, gas molecules travel only a small distance (compared to the ge-

ometry and ﬂow dimensions) between collisions. For internal ﬂows this means that

molecules only very rarely collide with walls, and the ﬂow is dominated by the

characteristics of the inter-molecular collisions. As a result, the gas will be in local

equilibrium and the velocity distribution of its molecules will be Maxwellian.

However, there are situations in which Kn is not so small, e.g. gas ﬂows at low

G. Abbate

Department of Multi-Scale Physics & J.M.Burgers Centre for Fluid Mechanics, Delft University of

Technology, Prins Bernhardlaan 6, 2628 BW Delft, The Netherlands e-mail: g.abbate@tudelft.nl

B.J. Thijsse

Department of Materials Science and Engineering, Delft University of Technology, Mekelweg 2,

2628 CD Delft, The Netherlands e-mail: b.j.thijsse@tudelft.nl

C.R. Kleijn

Department of Multi-Scale Physics & J.M.Burgers Centre for Fluid Mechanics, Delft University of

Technology, Prins Bernhardlaan 6, 2628 BW Delft, The Netherlands e-mail: c.r.kleijn@tudelft.nl

403

Lecture Notes in Computational Science and Engineering 71,

DOI 10.1007/978-3-642-03344-5_14,

B. Koren and C. Vuik (eds.), Advanced Computational Methods in Science and Engineering,

G. Abbate, B.J. Thijsse, and C.R. Kleijn

pressure, where

becomes large, or ﬂows with very small dimension L, e.g. mi-

croﬂuidics. The high Kn numbers in these ﬂows indicate that a molecule travels a

signiﬁcant distance (compared to L) between collisions. For an internal ﬂow, this

implies that wall interactions occur more frequently and become important in de-

scribing the ﬂow. In this regime, the ﬂow can no longer be described as a continuum

and the well known transport equations, or more precisely, the relations for the shear

tensor and the heat ﬂux, can no longer be used. In this regime, the particulate na-

ture of the gas becomes important and a different simulation method must be used.

The mathematical model at this level is the Boltzmann equation [1]. It provides in-

formation on the position, velocity and state of every molecule at all times. As a

consequence of its complexity, the Boltzmann equation is not amenable to analyti-

cal solution for non-trivial problems.

In the continuum regime, numerical simulations can be done using (commercially

available) Computational Fluid Dynamics (CFD) codes based on partial differen-

tial equations describing the transport phenomena, e.g. the Navier-Stokes equations.

Especially for laminar ﬂows, these codes can produce accurate results for Knudsen

numbers up to 0.01, but start deviating from reality for higher Kn. It is generally

accepted that the range of applicability of these continuum codes can be extended

into the rareﬁed regime up to Kn ≈ 0.1 by using special boundary conditions to take

into account the possibility of a velocity slip or temperature jump at a surface [2]. In

this method, however, the precise formulation of the slip velocity and temperature

jump boundary conditions is strongly geometry dependent [3, 4, 5].

Gas ﬂows with Kn > 10 are called ”free molecular ﬂows”. In this regime, inter-

molecular collisions rarely occur and the ﬂow is completely dominated by the inter-

action between the gas and the walls. Gas ﬂows in the free molecular regime can be

simulated using Molecular Dynamics (MD) or ballistic models.

In the intermediate (0.01 < Kn < 10) or rareﬁed regime, both collisions with solid

surfaces and with other gas molecules are important, and therefore have to be in-

cluded in the simulation to obtain an accurate result. The Direct Simulation Monte

Carlo (DSMC) method as developed by Bird [6] is the only practical engineering

method that can be used in the rareﬁed regime. The DSMC method is also valid

in free molecular and continuum regimes, although the computational expenses be-

come very large in the latter case. Its computational expenses, in fact, scale with

−4

and become prohibitively large when Kn becomes lower than ∼ 0.05.

In summary, one can simulate gas ﬂows with Kn < 0.01 (or, with modiﬁcations

of boundary conditions < 0.1) using continuum based CFD models, and gas ﬂows

with Kn > 0.05 with particle based DSMC methods. In many practical applications,

however, gas ﬂows undergo spatial and/or temporal transitions from low (< 0.05)

to high (> 0.05) Kn numbers, e.g. due to varying pressure or dimensions. Examples

include: ﬂow around vehicles at high altitudes, particularly re-entry of vehicles in a

planetary atmosphere [7], ﬂow through microﬂuidic gas devices [8], small cold gas

thruster nozzle and plume ﬂows [9], and low pressure thin ﬁlm deposition processes

from expanding plasma or gas jets [10].

Different solutions have been proposed to compute ﬂows undergoing such transi-

tions. The most widely studied method is to use hybrid models coupling contin-

404

Hybrid N-S/DSMC Simulations of Gas Flows with Rareﬁed-Continuum Transitions

uum solvers and molecular methods, for instance: Molecular Dynamics (MD) and

Navier-Stokes (N-S) equations [11], Boltzmann and N-S equations [12], Direct Sim-

ulation Monte Carlo (DSMC) and Stokes equations [8], DSMC and incompressible

N-S equations [13], DSMC and Euler equations [14] and DSMC and N-S equations

[15, 16, 17, 18, 19].

With respect to coupling N-S to DSMC, Garcia et al. [15] constructed a hybrid

particle/continuum algorithm with an adaptive mesh and algorithm reﬁnement, in

which DSMC was used as a particle method embedded within a Gudonov-type com-

pressible Navier-Stokes solver. There was no overlapping between the continuum

and DSMC regions, which were coupled through Neumann-Neumann type bound-

ary conditions. Glass and Gnoffo [16] proposed a ’one-shot’ coupled CFD-DSMC

method. The interfacial location between the CFD and DSMC zones was identiﬁed

manually after a ’one-shot’ CFD simulation. Results of the CFD simulation at this

interface were then used as Dirichlet inﬂow boundary condition for the DSMC in

the rareﬁed regions. In contrast with that, Wu et al. [17] and Schwartzentruber et al.

[18, 19] proposed an ’iterative’ coupled CFD-DSMC method, where the coupling

is achieved through an overlapped Schwarz method with Dirichlet-Dirichlet type

boundary conditions.

In the present chapter, we present a hybrid modeling approach for steady-state and

transient continuum/rareﬁed gas ﬂow, which employs the compressible N-S equa-

tions in the continuum regime and DSMC in the rareﬁed regime. The coupling of the

two models is reached through an overlapped Schwarz method [17] with Dirichlet-

Dirichlet boundary conditions. It is an adaptive method in which, during the compu-

tations, the Kn number with respect to the local gradients is computed to determine

the domain interface and divide the CFD domain from the DSMC domain. Our

method differs from that by Garcia et al. [15] in that we employ Dirichlet-Dirichlet

boundary conditions coupling, as opposed to Neumann-Neumann. The advantage is

that Dirichlet boundary conditions are much less sensitive to statistical scatter in the

DSMC simulations. The difference with the method proposed by Glass and Gnoffo

[16] is that we employ adaptive domain splitting based on dynamic evaluation of

local Kn numbers, rather than a pre-determined static interface. In contrast to Wu et

al. [17] and Schwartzentruber et al. [18, 19], who demonstrated methods for steady-

state ﬂows only, our present method can be applied to both steady-state and transient

ﬂows.

In section 2 we demonstrate how and under which conditions the Navier-Stokes

equations can approximate the Boltzmann equation. The developed hybrid numeri-

cal method is described in section 3. In particular, we ﬁrst describe the continuum

solver in section 3.2 and the DSMC solver in section 3.3. A description of the cou-

pling algorithm in both steady and unsteady formulations is given respectively in

sections 3.4.2 and 3.4.3. Results of applying the method to an unsteady 1-D shock

tube problem with a sensitivity analysis of the method to various parameters are

presented in section 4.1. Finally a validation of the method is performed by apply-

ing it respectively to a steady-state rareﬁed Poiseuille ﬂow, and a steady-state 2-D

expanding jet in a low pressure chamber, is presented in sections 4.2 and 4.3.

405

G. Abbate, B.J. Thijsse, and C.R. Kleijn

2 From Boltzmann to Navier-Stokes

The Navier-Stokes equations can be derived from the Boltzmann equation. The

derivation can be found in most texts on kinetic theory, e.g. Bird [6], Chapman

and Cowling [20], Grad [21], Patterson [22]. For the sake of completeness, the dis-

cussion is brieﬂy repeated here.

Considering an ideal mono-atomic gas in the absence of external forces and as-

suming the gas sufﬁciently dilute for binary collision to dominate, the Boltzmann

equation [1] reads

∂

(n f )

∂

+ c

∂

(n f )

∂



∂

(n f )

∂



coll

, (2)

where n is the number density, f is the velocity distribution function, c

the molec-

ular velocity in an inertial frame, the repeated index k denotes a sum, and the right-

hand side represents the collision integral. Multiplying the Boltzmann equation by

any function of molecular velocity Q(c

) and integrating over velocity space, the

moment equations are obtained

∂

(n < Q >)

∂

(n < c

Q >) =

∆

[Q]. (3)

In equation (3), the operators < Q > and

∆

[Q] are deﬁned by

< Q >=

∞

−∞

∞

−∞

∞

−∞

Q f dc

(4)

and

∆

[Q] =

∞

−∞

∞

−∞

∞

−∞

∂

(n f )

∂

coll

. (5)

Choosing one of the ﬁve collisional invariants Q

INV

= m{1, c

/2}, with m the

molecular mass and c

the square of the velocity magnitude, as the arbitrary function

of molecular velocity Q(c

), then the corresponding moment of the collision integral

is identically zero, i.e.

∆

[Q] = 0. This general result is valid for any distribution

function f and for any molecular interaction law and it leads to the conservation

laws for gas dynamics

∂

(n < Q

INV

>) +

∂

(n < c

INV

>) = 0. (6)

Considering the collisional invariants in turn, the following set of equations can be

written

∂

(

) +

∂

(

< c

>) = 0, (7)

∂

(

< c

>) +

∂

(

< c

>) = 0, (8)

406