Копитко М.Ф. Основи інформаційних технологій (на укр. языке)

Подождите немного. Документ загружается.

гіперпосилань, бо вони набрані за допомогою певних шрифтів або

відформатовані з використанням тих або інших ознак.

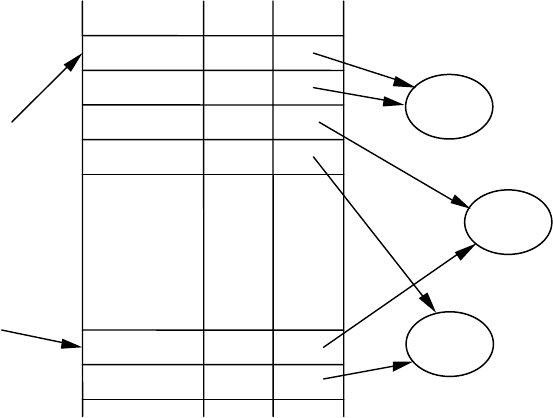
Приклад 54. На рис. 57 зображено файл сегментів, який дає

змогу знаходити екземпляри слів у документах формату HTML.

Комірка першого стовпця описує тип слова – приналежність

екземпляра слова певній складовій частині документа, ознаки

форматування слова і т.п. Значення у другому і третьому стовпцях

у сукупності утворюють покажчик на екземпляр слова в документі:

третя комірка містить посилання на документ, а друга представляє

номер слова в документі.

Тип Номер

Рис. 57. Звернений індекс з додатковою інформацією про екземпляри ключових

слів

Подібна структура даних дає змогу отримувати відповіді на

різні запити, що стосуються змісту документів, не потребуючи

детального вивчення кожного документа. Припустимо, наприклад,

100

ancho

title

header

title

text

cat

dog

doc1

doc2

doc3

151

що необхідно відшукати документи, які присвячено собакам і

містять згадки про котів. Якщо не вчитуватися у кожний документ

детально, то отримання чіткої відповіді на подібне запитання

доволі проблематичне. Загалом, непогану основу для подальшого

аналізу не важко забезпечити, якщо спробувати знайти документи,

в яких:

а) слово dog (собака) згадується у назві;

б) слово сat (кіт) міститься в областях тексту, які слугують

гіперпосиланнями (вказують на документи, присвячені

котам).

Щоб отримати відповідь на запити, достатньо здійснити

операцію перетину множин покажчиків. Покажчик у файлі індексу,

який відповідає ключовому слову cat, дає змогу визначити групу

покажчиків, що адресують екземпляри цього слова в документах.

Серед покажчиків групи-сегмента необхідно обрати такі, які

належать до типу anchor (область тексту гіперпосилання). Потім

відшукується група покажчиків, які посилаються на екземпляри

слова dog у документах, і у ній вибираються покажчики типу title

(назва). Операція перетину двох множин покажчиків визначить

набір посилань на документи, які задовольняють обидві умови:

слова dog присутні у назвах, а слова cat – в областях тексту

гіперпосилання.

9 Корисно знати. Файли сегментів: операція

вставляння і вилучення елементів. Структуру

файлів сегментів прийнято зображати (як це

зроблено, наприклад, на рис. 56) у вигляді ма-

сивів елементів. У реальності групи-сегменти

складаються із записів з єдиним полем

покажчика і зберігаються у блоках, як і будь-

які інші колекції записів. Отож у випадку мо-

дифікації файлів сегментів, що передбачає

вставляння і вилучення покажчиків, допустимо

використовувати прийоми, розглянуті вище: по-

передній розподіл записів по блоках, за якого

блоки заповнено не цілковито, що спрощує роз-

ширення файла в майбутньому; використання

блоків переповнення і переміщення записів усе-

редині блока і між блоками (в останньому ви-

152

падку необхідно потурбуватися і про відповідну

зміну вмісту покажчиків у зверненому індексі,

які посилаються на записи файла сегментів, що

переміщаються).

Вправи для опрацювання

Вправа 42. Під час здійснення операцій вставки записів у файл

даних і вилучення записів відповідного оновлення потребує і файл

вторинного індексу. Запропонуйте стратегії підтримки вторинного

індексу в актуальному стані за зміни файла даних.

Вправа 43. Розглянемо структуру компактно згрупованого

файла, подібну до наведеної на рис. 53, і припустимо, що в один

блок поміщаються десять записів даних, які представляють кортежі

відношень Movie або Studio. Припустимо також, що кількість

фільмів, які відповідають студії, рівномірно розподілено на

інтервалі від 1 до m. Як виглядає функція від m, яка обчислює

середнє число операцій дискового введення/виведення, необхідних

для отримання інформації про кіностудії і всі фільми, випущені

нею? Якою виявиться ця величина, якщо припустити, що розподіл

інформації про кінофільми у дискових блоках систематизовано?

Вправа 44. Припустимо, що кожен блок здатен зберігати три

записи даних, десять пар виду «ключ-покажчик» або п’ятдесят

покажчиків і передбачається використання схеми з проміжним

рівнем груп-сегментів (див. рис. 54).

1. Якщо кожне значення ключа пошуку міститься в

середньому в 10-ти записах, то скільки блоків необхідно

для зберігання 3 000 записів даних і відповідної структури

вторинного індексу? Скільки блоків необхідно було б

виокремити, якби не було файла сегментів?

2. Якщо обмежень на кількість записів даних з певним

значенням ключа пошуку немає, то яка мінімальна і

максимальна оцінка кількості необхідних блоків?

Вправа 45. Розширений варіант зверненого індексу, подібний до

наведеного на рис. 57, дає змогу виконувати запити різних видів.

Як можна використовувати цей індекс для відшукання документів,

в яких:

153

а) слова cat i dog чергуються на п’ятьох сусідніх позиціях

текстового фрагмента одного типу, наприклад, title (назва),

text (звичайний текст) або anchor (область гіперпосилання);

б) за словом dog розташовано довільне слово і слово cat;

в) слова dog і cat є в назві документа.

Тема 15. В-дерева

Хоча багаторівневі індекси вважають непоганим інструментом

пришвидшення процесів обробки запитів, існує узагальнений,

гнучкий та ефективний різновид структур, які найширше застосо-

вують у комерційних СКБД. Йдеться про структури, які називають

В-деревами (B-tree). Найпоширенішим є варіант В+-дерево

(B+-tree).

Особливості В-дерев такі:

• автоматична підтримка необхідної кількості рівнів індексації,

що відповідає розміру файла даних, який індексується;

• ефективне керування розміром вільних областей усередині

блоків (рівень заповнення блоків коливається від 50% до

100%) і відсутність потреби у використанні блоків

переповнення.

Нижче ми обговорюватимемо такі характеристики В-дерев, які

цілком справедливі для В+-дерев.

15.1. Структура В-дерева

Як випливає з назви структури В-дерева, її блоки організовані у

вигляді деревоподібного графа (tree-like graph). В-дерево є

збалансованим – у тому розумінні, що довжини всіх шляхів від

кореневої (root) вершини до будь-якої з вершин-листів (leaves) є

рівними. Типове В-дерево містить три рівні: кореневу вершину,

проміжні вершини і листи, − хоча може налічувати і довільну

кількість рівнів. Щоб отримати початкове уявлення про В-дерева,

погляньте на рис. 58 і 59, які описують окремі вершини, і на рис.60,

що зображає невелике повне В-дерево.

Кожному В-деревоподібному індексу відповідає параметр n,

який визначає властивості компонування блоків В-дерева. Кожен

блок має простір, достатній для розміщення n значень ключа

154

пошуку і n+1 покажчиків. Блок дерева насправді подібний до

індексних блоків, які розглянуто у темі 13, за винятком того, що

поряд з n парами виду «ключ-покажчик» він містить додатковий,

n+1-й, покажчик. Величина n обирається так, щоб забезпечити

можливість зберігання у блоці n+1 покажчиків і n ключових

значень.

Приклад 55. Нехай дисковий блок має розмір 4 096 байтів.

Припустимо, що функцію ключів виконують 4-байтові цілочислові

значення, а під кожен покажчик відведено по 8 байтів. Якщо

вважати, що блоки не містять заголовків, то найбільшим цілим

значенням n, яке задовольняє умову 4n+8(n+1) ≤ 4 096, буде 340.

Існує кілька важливих правил, які регламентують склад вмісту

блоків В-дерева.

• Ключові значення, які знаходяться у вершинах-листах, є

копіями ключів записів файла даних. Ключі розділені по

вершинах-листах зліва направо у порядку зростання

значень.

• Коренева вершина містить, щонайменше, два

покажчики, які адресують блоки вершини наступного

рівня В-дерева

чем.

• Останній покажчик вершини-листа посилається на

чергову вершину-лист справа, тобто на блок, який

містить наступну за порядком порцію ключових

значень. Щонайменше ⎣(n+1)/2⎦ з n покажчиків

блоці-листі використовують для посилання на записи

даних, а решта вважають вільними та інтерпретують

так, наче вони мають значення null; і-й покажчик, якщо

його використовують, адресує запис з і-м клю

Можлива ситуація, коли файл даних містить тільки один запис, отож

В-дерево складатиметься з єдиної вершини, яка володіє однією парою

виду «

ключ-покажчик» і є водночас і коренем, і листком. Подібний

вироджений випадок у подальшому ми ігноруватимемо.

Вирази ⎣x⎦ і ⎡x⎤ означають «найбільше ціле, менше від х» (виділення

цілої частини

х) і «найменше ціле, більше від х» (заокруглення х до

найближчого більшого цілого), відповідно.

155

• Усі n+1 покажчиків у проміжній вершині можна вико-

ристовувати для посилання на блоки наступного рівня

В-дерева, хоча реально повинні використовуватися

щонайменше ⎡(n+1)/2⎤ з них (нагадаємо, що, незалежно

від величини n, коренева вершина може містити не

менше, ніж 2 покажчики, які використовуються за

призначенням). Якщо діючими є j покажчиків, то їм

відповідають j-1 ключів (наприклад, К

, К

, ..., К

j-1

Перший покажчик адресує ту частину В-дерева, яка дає

змогу відшукати записи з ключовими значеннями,

меншими К

. Другий покажчик посилається на фрагмент

дерева, відповідальний за виявлення записів зі

значеннями ключа, які більші або дорівнюють К

строго менші від К

, і т.д. Зрештою, j-й покажчик

приводить до гілки дерева, яка відповідає записам з

ключовими значеннями, рівними або більшими К

j-1

Зауважимо, що записи з ключами, набагато меншими

від К

і значно більшими від К

j-1

, з біжучого блока,

можливо, і недосяжні – у такому випадку їм відповіда-

тимуть певні сусідні блоки, які належать до того ж рівня

дерева.

Приклад 56. У цьому і наступних прикладах, що стосуються В-

дерев, ми вважатимемо, що n = 3, тобто кожен блок може містити

три ключових значення, які є невеликими (це припущення цілком

правдоподібне) цілими числами, і чотири покажчики. На рис. 58

проілюстровано вершину-лист, усі покажчики якої використано за

призначенням. Блок вершини містить три ключі – 57, 81 і 95. Перші

три покажчики адресують записи даних з зазначеними ключами, а

останній (як і в будь-якому листі В-дерева) посилається на сусідній

лист справа від біжучого. Якщо біжуча вершина-лист є останньою,

то покажчику присвоюється значення null.

Ми вже говорили, що допустимо не заповнювати блок-лист до

кінця, але в нашому випадку (за умови n = 3) блок повинен

містити, як мінімум, дві пари виду «ключ-покажчик» (у схемі на

рис. 58 ключ 95 і відповідний йому покажчик, зазначений як «До

запису з ключем 95» можуть бути відсутніми).

156

57 81 95

До наступного

Рис. 58.Схематичне зображення типової вершини-листа В-дерева

На рис. 59 зображено звичайну проміжну вершину В-дерева.

Вона містить три ключі (ми обрали ті ж значення, що і в зразку

вершини-листа, проілюстрованому на рис. 58 – 57, 81 і 95)

чотири покажчики. Перший покажчик посилається на гілку дерева,

яка дає змогу звертатися до записів з ключами, меншими від 57.

Другий покажчик здатний привести до записів з ключовими

значеннями з проміжку від 57 (включно) до 81, третій – до записів з

ключами з інтервалу від 81 (включно) до 95, а четвертий – до

записів, значення ключів яких не менше від 95.

Як і в розглянутому вище прикладі листа В-дерева, зовсім не

обов’язково, щоб були зайнятими всі «комірки», призначені для

зберігання ключів і покажчиків. Однак у випадку n=3 проміжна

вершина повинна містити щонайменше один ключ і два

покажчики. Найекстремальнішим варіантом виявився б такий, коли

блок містить ключ 57 і тільки два початкових покажчики: перший з

них адресує ключі, менші від 57, а другий − більші або рівні 57.

Не дивлячись на збігання ключових значень, листок на рис. 58 і

проміжна вершина на рис. 59 ніяк між собою не пов’язані. Більше того,

цілком можливо, що вони ніколи не будуть одночасно представлені в

одному і тому ж

В-дереві.

листа

До запису До запису До запису

з ключем з ключем з ключем

57 81 95

157

57 81 95

До ключів

81 ≤ Κ < 95

До ключів

K < 57

До ключів

57 ≤ Κ < 81

До ключів

Κ ≥ 95

Рис. 59. Приклад проміжної вершини В-дерева

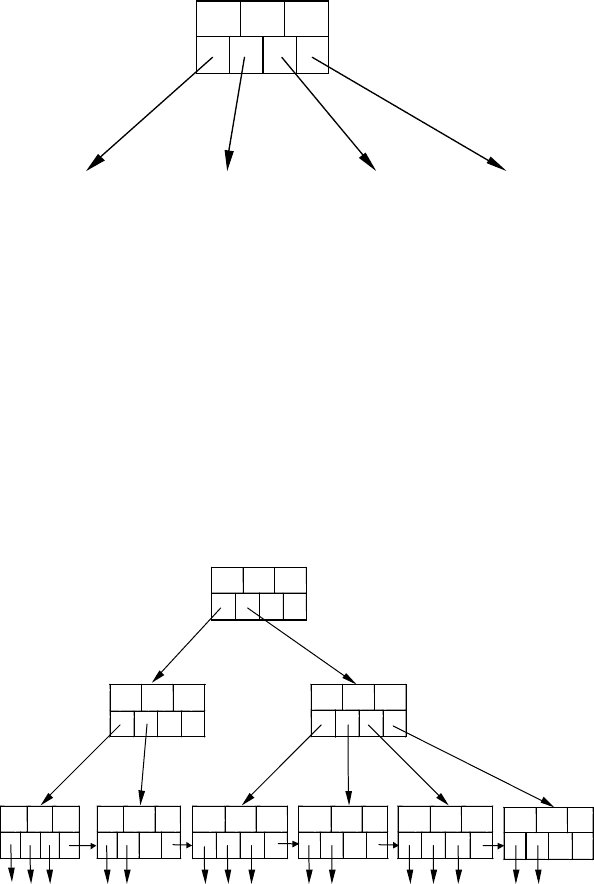
Приклад 57. На рис. 60 зображене В-дерево, що має три рівні та

містить вершини, зразки яких розглянуто у прикладі 56. Вважають,

що файл даних складається з записів, ключові значення яких є

простими числами з інтервалу від 2 до 47. Зверніть увагу, що на

рівні вершин-листів кожен ключ не повторюється двічі, і ключі

впорядковано за зростанням від «лівих» вершин до «правих».

Кожен блок-лист містить від двох до трьох пар виду «ключ-

покажчик», а також покажчик, який адресує наступний лист

послідовності.

Рис. 60. Приклад В-дерева

158

Коренева вершина містить тільки два покажчики (мінімально

можливу кількість), хоча могла б налічувати до чотирьох. Єдиний

ключ кореневої вершини ділить множину ключів на дві частини:

одна доступна за посередництвом першого покажчика, а друга –

другого. Ключі зі значеннями 2-11 (не 2-12, як здається, оскільки за

нашою домовленістю ключі є простими числами) можна відшукати

в лівому піддереві відносно кореневої вершини, а ключі зі

значеннями 13 і вище – у правому.

Перша (ліва) дочірня вершина кореневої вершини, що містить

ключ 7, також володіє двома покажчиками, перший з яких

посилається на ключі, менші від 7, а другий – на ключі, більші або

рівні 7. Зауважимо, що другий покажчик дає змогу звернутися до

ключів 7 і 11, а не до всіх ключів, не менших від 7 (наприклад, 13),

− решта ключів досяжні із сусідньої проміжної вершини дерева.

Зрештою, друга (права) дочірня вершина містить всі чотири

покажчики. Перший адресує підмножину ключів, менших від 23

(а саме – 13, 17 і 19), другий посилається на ключі К, які задо-

вольняють умову 23≤K<31, третій дає змогу знайти ключі, такі, що

31≤K<43, а четвертий приводить до підмножини ключів К≥43.

15.2. Використання В-дерев

Модель В-дерева є потужним інструментом конструювання

індексів. Послідовність покажчиків на записи, які містяться у

вершинах-листах, здатна виконувати ті ж функції, що і будь-яка

підмножина покажчиків у «традиційних» індексних файлах, які

розглянуто у темах 13 і 14.

Наведемо декілька прикладів.

1. Ключ пошуку в В-дереві є первинним ключем файла

даних, індекс належить до категорії щільних. Іншими

словами, блоки-листи індексу містять по одній парі

«ключ-покажчик» для кожного запису даних. Файл

даних може бути (або може і не бути) посортованим за

первинним ключем.

2. Файл даних є посортованим за первинним ключем, і

В-дерево фігурує як розріджений індекс, листи якого

містять по одній парі виду «ключ-покажчик» для

кожного блока даних.

159

3. Файл даних є посортованим за значеннями атрибута,

який не є первинним ключем, і цей атрибут слугує

ключем пошуку в В-дереві. Для кожного ключового

значення К, яке присутнє в записах даних, у деякому

блоці-листі існує одна пара виду «ключ-покажчик», і

покажчик адресує перший із записів, що володіють

значенням К.

Варіанти В-дерев, що допускають наявність дублікатів значень

ключа пошуку

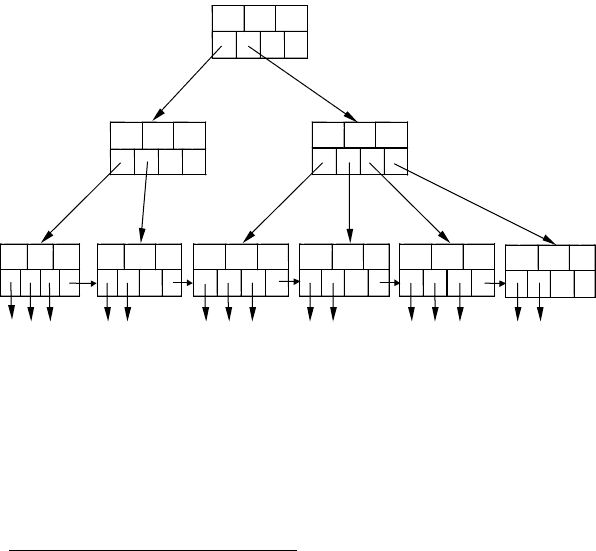
, також мають широке використання. Приклад

подібного В-дерева представлено на рис. 61, і він ілюструє

розширену модель В-дерев, аналогічну до схеми «звичайних»

індексів зі значеннями ключа, що повторюються (див. пункт 13.5).

Рис. 61. В-дерево з дублікатами значень ключа

Якщо ключ В-дерева допускає наявність значень-дублікатів,

необхідно трохи переглянути спосіб інтерпретації ключів, які

належать проміжним вершинам (ми говорили про це у пункті 15.1).

Припустимо, що проміжна вершина містить ключові значення

,К

,...,К

. Тоді К

буде найменшим новим значенням, присутнім у

Нагадаємо, що термін ключ пошуку не завжди засвідчує унікальність

ключових значень

160