Контрольная работа - Сложные проценты + 6 задач
Подождите немного. Документ загружается.

Кафедра «Финансы и кредит»
«Финансовая математика»
Вариант №53
Калининград 2009
СОДЕРЖАНИЕ
Введение;
1. Сложные проценты: понятие и область применения;
2. Задачи;
Список использованных источников.
2
Введение
В любой развитой рыночной экономике процентная ставка в
национальной валюте является одним из самых важных макроэкономических
показателей, за которым пристально следят не только профессиональные
финансисты, инвесторы и аналитики, но также предприниматели и простые
граждане. Причина такого внимания ясна: процентная ставка - это самая
главная цена в национальной экономике: она отражает цену денег во
времени. Кроме того, двоюродная сестра процентной ставки - это уровень
инфляции, измеряемый также в процентных пунктах и признаваемый в
соответствии с монетаристской парадигмой одним из главных ориентиров и
результатов состояния национальной экономики (чем меньше инфляция, тем
лучше для экономики, и наоборот). Родственная связь здесь проста: уровень
номинальной процентной ставки должен быть выше уровня инфляции, при
этом оба показателя измеряются в процентах годовых. В современной
экономической теории общий термин "процентная ставка" используется в
единственном числе. Здесь она рассматривается в качестве инструмента, с
помощью которого государство в лице монетарных властей воздействует на
экономический цикл страны, сигнализируя об изменении кредитно-денежной
политики и изменяя объем денежной массы в обращении. На частном уровне
в повседневной практической жизни ссудный процент пронизывает всю
экономическую жизнь страны, присутствуя в различных кредитных и
долговых инструментах государства, банков, компаний, индивидуальных
предпринимателей и частных лиц в виде разнообразных процентных ставок.
3
1. Сложные проценты: понятие и область применения.
В средне- и долгосрочных финансово-кредитных операциях, если
проценты не выплачиваются сразу после их начисления, а присоединяются к
сумме долга (депозита), применяются сложные проценты (compound interest).
База для начисления сложных процентов в отличие от простых, не остается
постоянной - она увеличивается каждым шагом во времени. Абсолютная
сумма начисленных процентов возрастает, и процесс увеличения суммы
долга (депозита) происходит с ускорением. Наращение по сложным
процентам можно представить как последовательное реинвестирование
средств, вложенных под простые проценты на один период начисления
(running period). Присоединение начисленных процентов к сумме, которая
послужила базой для их начисления, часто называют капитализацией
процентов.
Для нахождения формулы расчета наращенной суммы, при условии, что
проценты начисляются и капитализируются один раз в году (годовые
проценты), применяется сложная ставка наращения. Для записи формулы
наращения применяются те же обозначения, что и в формуле наращения по
простым процентам:
P – первоначальный размер долга (ссуды, кредита, капитала и т.д.),
S – наращенная сумма на конец срока ссуды,
n – срок, число лет наращения,
i – уровень годовой ставки процентов, представленной десятичной дробью.
Основные формулы при определении начисленных процентов и
наращенной суммы при использовании схемы сложных процентов:
S = P * ( 1 + i )
n
(1)
I = S – P = P * | ( 1 + i )
n
– 1 | (2)
I
p
= P * | ( 1 + i )
n
– ( 1 + n * i ) | (3)
Как показано выше, рост по сложным процентам представляет собой
процесс, соответствующий геометрической прогрессии, первый член которой
4
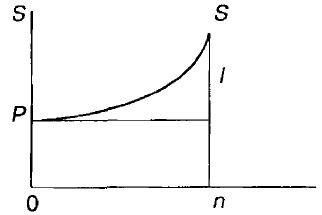
равен P, а знаменатель – (1 + i). Последний член прогрессии равен
наращенной сумме в конце срока ссуды. Графически иллюстрация по
сложным процентам представлена на рис. 1.
Рис. 1.
Величину (1 + i)
n
называют множителем наращения (compound
interest factor) по сложным процентам. Точностью расчета множителя в
практических расчетах определяется допустимой степенью округления
наращенной суммы (до последней копейки, рубля, и т.д.).
Время при наращении по сложной ставке обычно измеряется как ACT/
ACT или 365/365.
Областью применения сложных процентов является сфера финансов и
кредита, т.е. главным образом банковская, инвестиционная и страховая
деятельность.
5
2. Задачи
2.1. Задача №1.
Создается фонд денежных средств путем внесения на депозит по
150Y000 в конце каждого года. Банк платит 10% годовых. Проценты
начисляются раз в год по схеме сложных процентов. Определить сумму
фонда к концу 4-х лет.
Формула:
S = R * ((1 + i)
n
- 1) : i
где,
R – постоянная величина депозита;
i – постоянная годовая величина процентной ставки;
n – количество периодов внесения депозитов и начисления процентов, то
150Y000 * ((1 + 0,1)
4
- 1) : 0,1 = 150Y000 * 0,46 : 0,1 = 696 150
Ответ: таким образом, к концу четвертого года на счете будет 696Y150
рублей, в том числе 600Y000 рублей это собственные деньги вкладчика и
96Y150 рублей начисленные проценты.
6
2.2. Задача №2.
Чистые денежные потоки по годам прогнозируются в следующих
объемах: 1-й год – 50Y000 рублей, 2-й год – 56Y000 рублей, 3-й год – 75Y000
рублей, 4-й год – 80Y000 рублей. Стоимость капитала 20% (сложные
проценты).
Определить: приведенную стоимость проекта.
Прежде всего, найдем множитель дисконтирования (r) по формуле:
r = 1 / ( 1 + i )
n
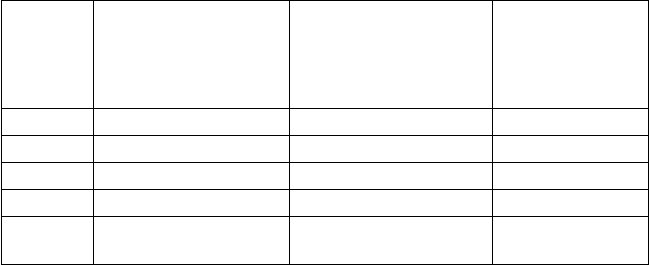
Годы
Прогнозируемы
е
денежные
потоки
Множитель
дисконтировани
я,
r = 20%
Приведенна
я
стоимость
1 50 000 0.833 41 667
2 56 000 0.694 38 889
3 75 000 0.579 43 403
4 80 000 0.482 38 580
ИТОГ
О: 261 000 162 539
Таким образом, «сегодняшняя стоимость» проекта в течение четырех лет
261Y000 с учетом коэффициента дисконтирования 20% составляет 162 539
(что меньше на 98Y461 рублей)
7
2.3. Задача №3.
Вклад в размере 20Y000 рублей помещен в банк 19.01. и востребован
27.03. под ставку процентов 15% годовых.
Определить сумму начисленных процентов и наращенную сумму при
различных методах определения срока начисления.
S = P + I = P * (1 + n * i ),
где,
n = t / k,
t – срок депозита,
k – временная база, 360 дней (12 месяцев по 30 дней) или 365 (366) дней, т.е.
полноценный календарный год.
1. Точные проценты с точным числом дней депозита (365/365):
20Y000 * (1 + 67 / 365 * 0.15) = 20Y550,69 рублей, сумма начисленных
процентов составит550,69 рублей.
2. Обыкновенные проценты с точным числом дней депозита (360/365):
20Y000 * (1 + 67 / 360 * 0.15) = 20Y558,33 рублей, сумма начисленных
процентов составит 558,33 рублей.
3. Обыкновенные проценты с приблизительным числом дней депозита
(360/360):
20Y000 * (1 + 68 / 360 * 0.15) = 20Y566,67 рублей, сумма начисленных
процентов составит 566,67 рублей.
Вывод: для вкладчика, более выгодным является 3-й метод расчета срока
начисления процентов на вложенный депозит.
8
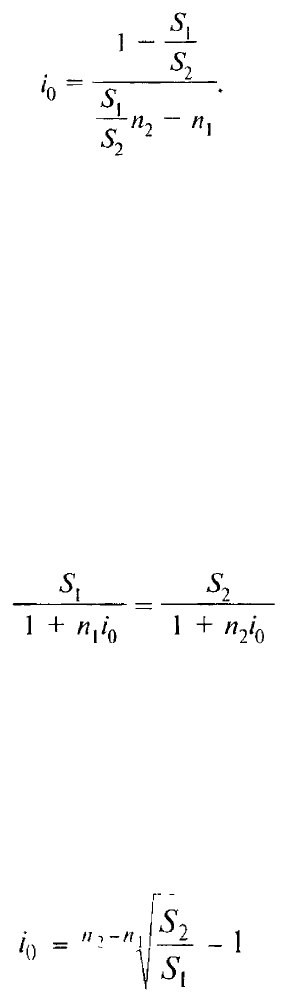
2.4. Задача №4.
Платеж в 60Y000 рублей через 2 года, заменяется на платеж в 80Y000
рублей через 4 года.
Найти критический уровни простой и сложной процентных ставок.
Как изменяться финансовые отношения сторон, если в расчетах будет
использоваться 25%.
1) Найдем критическую ставку по простой процентной ставке по
формуле:
где
S
1
= 60Y000
S
2
= 80Y000
n
1
= 2
n
2
= 4
i
0
= (1 - 60Y000 / 80 000) / (60Y000 / 80Y000 * 2 - 4) = 0,25 / 1 = 0,25 или 25,0%
Проверим на основе равенства:
60Y000 / (1 + 2 * 0,25) = 80 000 / (1 + 4 * 0,25)
40Y000 = 40Y000
2) Найдем критическую ставку по простой процентной ставке по
формуле:
9
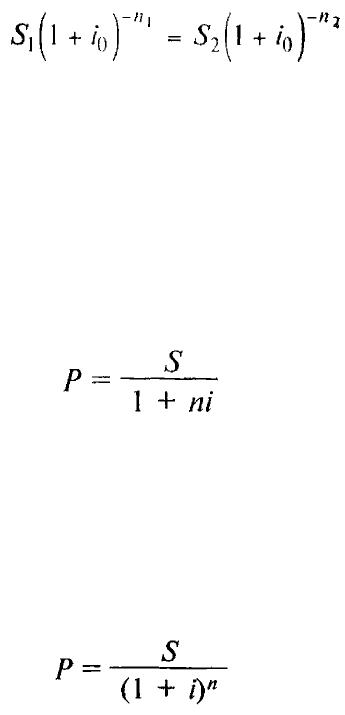
i
0
= 4 – 2 КОРЕНЬ (80Y000 / 60Y000 - 1) = 0,1547 или 15,47%
Проверим на основе равенства:
60Y000 * (1 + 0,1547)
-2
= 80Y000 * (1 + 0,1547)
-4
45Y000 = 45Y000
3) Сравним условия кредита с использованием 25% годовых.
Найдем первоначальную сумму кредита исходя из простых процентов:
P
1
= 60Y000 / (1 + 2 * 0,25) = 40Y000
P
2
= 80Y000 / (1 + 4 * 0,25) = 40Y000
Найдем первоначальную сумму кредита исходя из сложных процентов:
P
1
= 60Y000 / (1 + 0,25)
2
= 38Y400
P
2
= 80Y000 / (1 + 0,25)
4
= 32Y768,1
Таким образом, при использовании 25% годовой ставке,
первоначальная сумма кредита по простым процентам не измениться, т.е.
останется 40Y000 рублей при кредите 60Y000 через 2 года и 80Y000 через 4
года, а при использовании сложной процентной ставке, первоначальная
сумма кредита в 80Y000 через 4 года будет меньше кредита в 60Y000 через 2
года, и соответственно сумма процентов за использование данного кредита
выше.
10
