Контрольная работа по эконометрике
Подождите немного. Документ загружается.


Автономная некоммерческая организация высшего профессионального образования
«ПЕРМСКИЙ ИНСТИТУТ ЭКОНОМИКИ И ФИНАНСОВ»
Контрольная работа по эконометрике
Вариант№ 3
Пермь 2010
Задание 1.
№ магазина Годовой
товарооборот,
млн. руб., y
Торговая
площадь, тыс.
кв.м., х
1 19,76 0,24
2 38,09 0,31
3 40,95 0,55
4 41,08 0,48
5 56,29 0,78
6 68,51 0,98
7 75,01 0,94
8 89,05 1,21
9 91,13 1,29
10 91,26 1,12
11 99,84 1,29
12 108,55 1,49
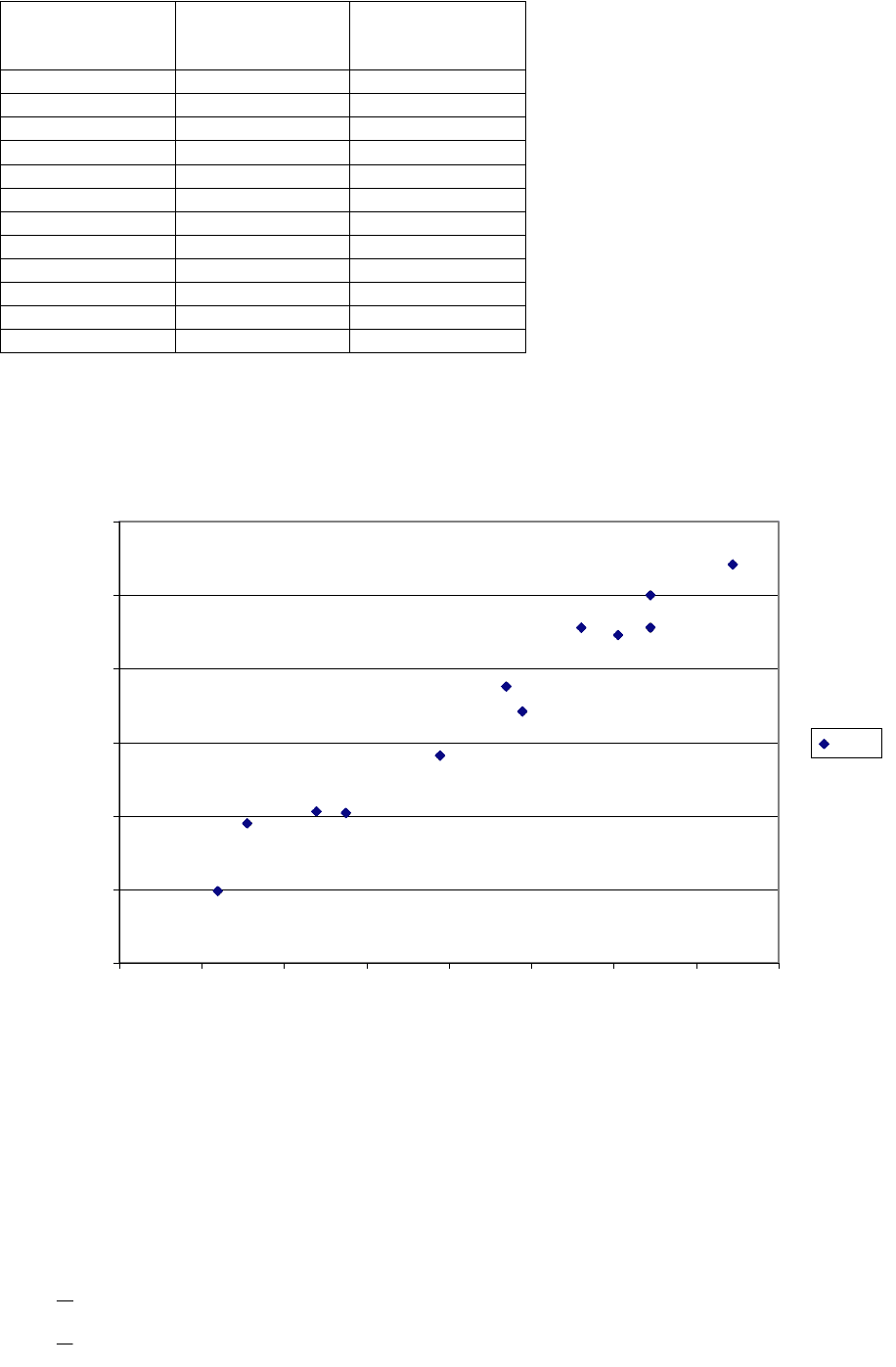
По данным из таблицы, выполнить следующие действия
1. Построить поле корреляции и сформулировать гипотезу о форме связи.
0
20
40
60
80
100
120
0 0,2 0,4 0,6 0,8 1 1,2 1,4 1,6
Ряд1
2. Рассчитать параметры уравнений линейной, степенной, экспоненциальной,
полулогарифмической, обратной, гиперболической парной регрессии.
Линейная регрессия
y = ax+b
Cоставим систему нормальных уравнений по МНК.
ii
iiii
ii
iii
ii
ybnxa
yxxbxa
baxy
b
s
xbaxy
a
s
baxys
2
2
012
02
2

Расчётная таблица
y x
x
2
xy
19,79
0,24 0,0576 4,7496
38,09
0,31 0,0961 11,8079
40,95
0,55 0,3025 22,5225
41,08
0,48 0,2304 19,7184
56,29
0,78 0,6084 43,9062
68,51
0,98 0,9604 67,1398
75,01
0,94 0,8836 70,5094
89,05
1,21 1,4641 107,7505
91,13
1,29 1,6641 117,5577
91,26
1,12 1,2544 102,2112
99,84
1,29 1,6641 128,7936
108,55
1,49 2,2201 161,7395
819,55 10,68 11,4058 858,4063
9,79,67
9,7
81,22
84,179
;9,67
81,22
08,1548
84,179
55,81968,10
41,85841,11
;08,1548
1255,819
68,1041,858
;81,22
1268,10
68,1041,11
;
55,8191268,10
41,85868,1041,11
xy
ba
b
a
b
b
a
a
ba
ba
Степенная регрессия
b
axy
Cоставим систему нормальных уравнений по МНК.
xyxBxA
yxBAn
xxBAy
b
s
xBAy
a
s
xBAys
xBAy
BbAa
xbay
axy
i
ii
iii
i
ii
b
lnlnlnln
lnln
0lnlnln2
01lnln2
lnln
lnln
,;ln
lnlnln
lnln
2
2
Расчётная таблица
y x lnx lny
ln
2
x lnx*lny
19,79
0,24 -1,43 2,99 2,04 -4,26
38,09
0,31 -1,17 3,64 1,37 -4,26
40,95
0,55 -0,60 3,71 0,36 -2,22
41,08
0,48 -0,73 3,72 0,54 -2,73
56,29
0,78 -0,25 4,03 0,06 -1,00
68,51
0,98 -0,02 4,23 0,00 -0,09
75,01
0,94 -0,06 4,32 0,00 -0,27
89,05
1,21 0,19 4,49 0,04 0,86
91,13
1,29 0,25 4,51 0,06 1,15
91,26
1,12 0,11 4,51 0,01 0,51
99,84
1,29 0,25 4,60 0,06 1,17
108,55
1,49 0,40 4,69 0,16 1,87
819,55 10,68 -3,05 49,43 4,71 -9,27
8,0
9,75
8,08,0
9,7533,4
84,0
21,47
51,3 9
;33,4
21,47
5,204
51,3 9
27,905,3
43,491 2
;5,204
71,427,9
05,343,49
;2 1,47
71,405,3
05,312
;
27,971,405,3
43,4905,312
xy
bB
aA
BA
BA
B
B
A
A
BA
BA
Экспоненциальная регрессия
bx
aey
3

Cоставим систему нормальных уравнений по МНК.
xyxBxA
yxBAn
xBxAy
b
s
BxAy
a
s
BxAys
BxAy
BbAa
bxay
aey
i
i
ii
iii
i
ii
bx
ln
ln
0ln2
01ln2
ln
ln
,;ln
lnln
lnln
2
2
Расчётная таблица
y x
х
2
lny lnу*х
19,79
0,24 0,06 2,99 0,72
38,09
0,31 0,10 3,64 1,13
40,95
0,55 0,30 3,71 2,04
41,08
0,48 0,23 3,72 1,78
56,29
0,78 0,61 4,03 3,14
68,51
0,98 0,96 4,23 4,14
75,01
0,94 0,88 4,32 4,06
89,05
1,21 1,46 4,49 5,43
91,13
1,29 1,66 4,51 5,82
91,26
1,12 1,25 4,51 5,06
99,84
1,29 1,66 4,60 5,94
108,55
1,49 2,22 4,69 6,98
819,55 10,68 11,41 49,43 46,25
x
ey
bB
aA
BA
BA
B
B
A
A
BA
BA
18,1
45,21
18,118,1
45,2107,3
18,1
81,22
99,2 6
;07,3
81,22
93,6 9
99,2 6
25,4668,10
43,4912
;93,69
41,1125,46
68,1 043,4 9
;8 1,22
41,1168,10
68,1 012
;
25,4 641,1168,10
43,4 968,1 012
Полулогарифмическая регрессия
bxay ln
Cоставим систему нормальных уравнений по МНК.
ii
iiii
ii
iii
ii
ybnxa
xyxbxa
bxay
b
s
xbxay
a
s
bxays
ln
lnlnln
01ln2
0lnln2
ln
2
2
Расчётная таблица
y x lnx
ln
2
x lnx*y
19,79
0,24 -1,43 2,04 -28,24
38,09
0,31 -1,17 1,37 -44,61
40,95
0,55 -0,60 0,36 -24,48
41,08
0,48 -0,73 0,54 -30,15
56,29
0,78 -0,25 0,06 -13,99
68,51
0,98 -0,02 0,00 -1,38
75,01
0,94 -0,06 0,00 -4,64
89,05
1,21 0,19 0,04 16,97
91,13
1,29 0,25 0,06 23,21
91,26
1,12 0,11 0,01 10,34
99,84
1,29 0,25 0,06 25,42
108,55
1,49 0,40 0,16 43,29
819,55 10,68 -3,05 4,71 -28,26
4
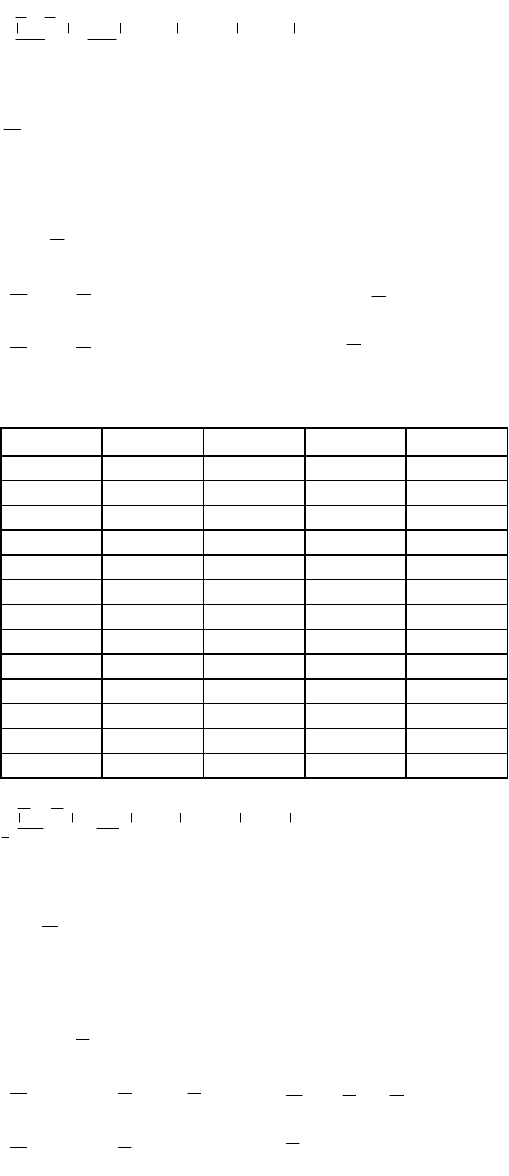
6,79ln7,4 5
6,79
21,47
53,3772
;7,45
21,47
34,2159
53,3772
55,81 905,3
26,2871,4
;3 4,2159
1255,8 19
05,326,2 8
;21,47
1205,3
05,371,4
;
55,81 91205,3
26,2805,37 1,4
xy
Ba
ba
b
b
a
a
ba
ba
Обратная регрессия
bax
y
1
Cоставим систему нормальных уравнений по МНК.
i
i
i
i
ii
i
i
ii
i
i
i
y
bnxa
y
x
xbxa
bax
yb
s
xbax
ya
s
bax
y
s
1
01
1
2
0
1
2
1
2
2
Расчётная таблица
y x
x
2
1/у х/у
19,79
0,24 0,0576 0,051 0,012
38,09
0,31 0,0961 0,026 0,008
40,95
0,55 0,3025 0,024 0,013
41,08
0,48 0,2304 0,024 0,012
56,29
0,78 0,6084 0,018 0,014
68,51
0,98 0,9604 0,015 0,014
75,01
0,94 0,8836 0,013 0,013
89,05
1,21 1,4641 0,011 0,014
91,13
1,29 1,6641 0,011 0,014
91,26
1,12 1,2544 0,011 0,012
99,84
1,29 1,6641 0,010 0,013
108,55
1,49 2,2201 0,009 0,014
819,55 10,68 11,41 0,22 0,15
04,00 2,0
1
04,0
81,22
92,0
;02,0
81,22
56,0
92,0
22,068,10
15,041,11
;56,0
1222,0
68,1 015,0
;81,22
1268,10
68,1 04 1,11
;
22,01268,10
15,068,1041,11
x
y
ba
ba
b
b
a
a
ba
ba
Гиперболическая регрессия
b
x
a
y
Cоставим систему нормальных уравнений по МНК.
i
i
i
i
ii
i
i
ii
i
i
i
ybn
x
a
x
y
x
b
x
a
b
x
ay
b
s
x
b
x
ay
a
s
b
x
a
ys
1
11
01
1
2
0
11
2
2
2
Расчётная таблица
5
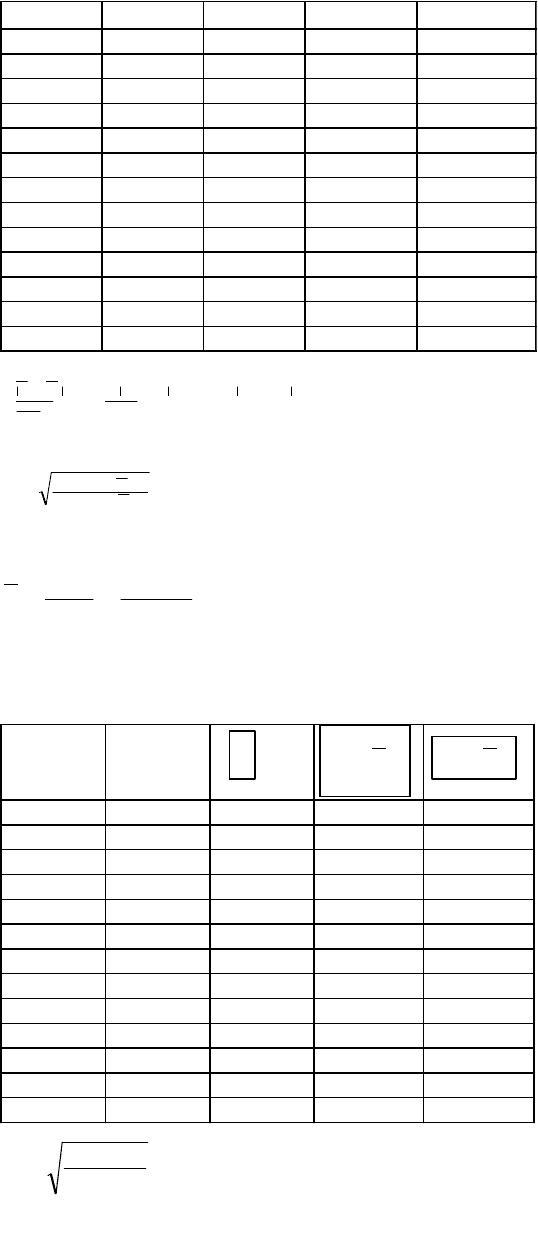
y x 1/х
1/х
2
у/х
19,79
0,24 4,166667 17,361111 82,458333
38,09
0,31 3,225806 10,405827 122,870968
40,95
0,55 1,818182 3,305785 74,454545
41,08
0,48 2,083333 4,340278 85,583333
56,29
0,78 1,282051 1,643655 72,166667
68,51
0,98 1,020408 1,041233 69,908163
75,01
0,94 1,063830 1,131734 79,797872
89,05
1,21 0,826446 0,683013 73,595041
91,13
1,29 0,775194 0,600925 70,643411
91,26
1,12 0,892857 0,797194 81,482143
99,84
1,29 0,775194 0,600925 77,395349
108,55
1,49 0,671141 0,450430 72,852349
819,55 10,68 18,60 42,36 963,21
5,103
7,22
49,103
34,162
13,16801
;71,2 2
34,162
04,3686
13,16801
55,8196,18
21,9633 6,42
;04,3686
1255,819
6,1821,963
;34,162
126,18
6,1836,42
;
55,819126,18
21,9636,1836,42
x
y
ba
ba
b
b
a
a
ba
ba
3. Оценить тесноту связи с помощью коэффициентов корреляции и детерминации
2
2
^
yy
yy
индекс корреляции
22
R
коэффициент детерминации
3,68
12
55,819
n
y
y
3.1. Для линейной регрессии
Расчётная таблица
y x
19,79
0,24 24,196 1945,1628 2353,2201
38,09
0,31 28,949 1548,5012 912,6441
40,95
0,55 45,245 531,53303 748,0225
41,08
0,48 40,492 773,28486 740,9284
56,29
0,78 60,862 55,323844 144,2401
68,51
0,98 74,442 37,724164 0,0441
75,01
0,94 71,726 11,737476 45,0241
89,05
1,21 90,059 473,45408 430,5625
91,13
1,29 95,491 739,35048 521,2089
91,26
1,12 83,948 244,8599 527,1616
99,84
1,29 95,491 739,35048 994,7716
108,55
1,49 109,071 1662,2744 1620,0625
819,55 10,68 819,97 8762,56 9037,89
^
y
2
^
yy
2
yy
98,0
89,9037
56,8762
индекс корреляции
97,0
2
R
коэффициент детерминации
3.2. Для степенной регрессии
Расчётная таблица
6
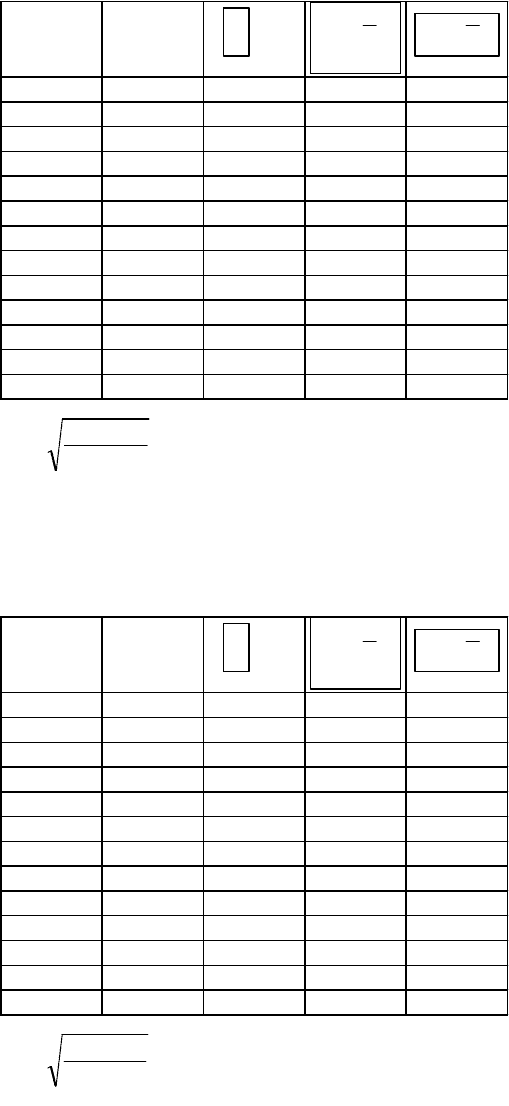
y x
19,79
0,24 24,2332 1941,883 2353,22
38,09
0,31 29,73933 1486,926 912,6441
40,95
0,55 47,047 451,69 748,0225
41,08
0,48 42,19245 681,6041 740,9284
56,29
0,78 62,2182 36,98826 144,2401
68,51
0,98 74,68315 40,74462 0,0441
75,01
0,94 72,2344 15,47949 45,0241
89,05
1,21 88,40362 404,1557 430,5625
91,13
1,29 93,04939 612,5325 521,2089
91,26
1,12 83,1029 219,1259 527,1616
99,84
1,29 93,04939 612,5325 994,7716
108,55
1,49 104,4217 1304,778 1620,063
819,55 10,68 814,37 7808,44 9037,89
^
y
2
^
yy
2
yy
93,0
89,9037
44,7808
индекс корреляции
86,0
2
R
коэффициент детерминации
3.3. Для экспоненциальной регрессии
Расчётная таблица
y x
19,79
0,24 24,48999 1919,317 2353,22
38,09
0,31 26,59875 1738,994 912,6441
40,95
0,55 35,3064 1088,577 748,0225
41,08
0,48 32,50729 1281,118 740,9284
56,29
0,78 46,31493 483,3433 144,2401
68,51
0,98 58,64277 93,262 0,0441
75,01
0,94 55,93914 152,7908 45,0241
89,05
1,21 76,92757 74,43502 430,5625
91,13
1,29 84,54335 263,8463 521,2089
91,26
1,12 69,17672 0,768636 527,1616
99,84
1,29 84,54335 263,8463 994,7716
108,55
1,49 107,0466 1501,3 1620,063
819,55 10,68 702,04 8861,60 9037,89
^
y
2
^
yy
2
yy
99,0
89,9037
6,8861
индекс корреляции
98,0
2
R
коэффициент детерминации
3.4. Для полулогарифмической регрессии
Расчётная таблица
7
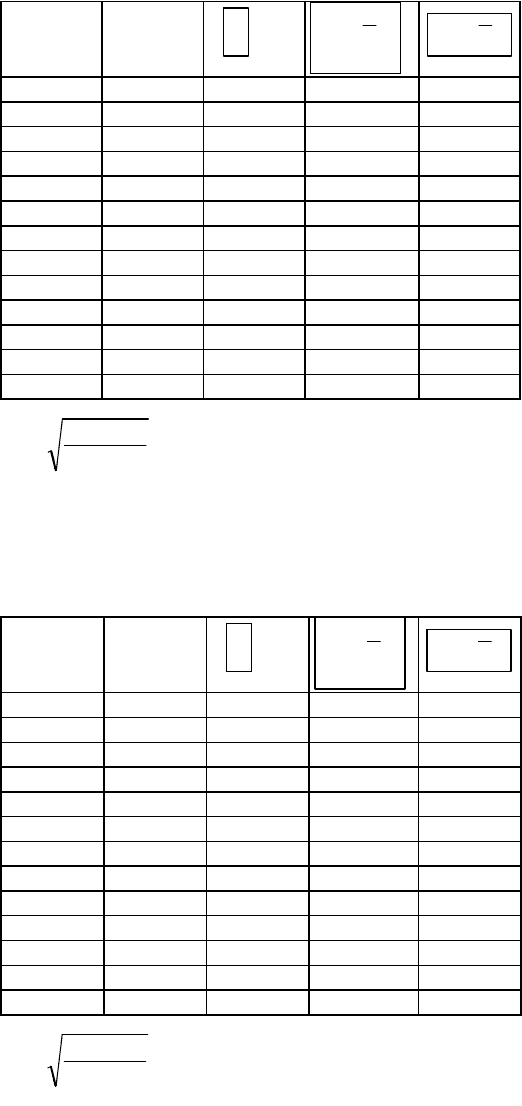
y x
19,79
0,24 14,38078 2907,282 2353,22
38,09
0,31 26,07694 1782,787 912,6441
40,95
0,55 52,27885 256,67728 748,0225
41,08
0,48 46,05761 494,72397 740,9284
56,29
0,78 68,24532 0,0029904 144,2401
68,51
0,98 78,67674 107,67666 0,0441
75,01
0,94 76,77229 71,779766 45,0241
89,05
1,21 88,31135 400,45415 430,5625
91,13
1,29 91,23715 526,11282 521,2089
91,26
1,12 84,77912 271,56143 527,1616
99,84
1,29 91,23715 526,11282 994,7716
108,55
1,49 97,82407 871,67063 1620,063
819,55 10,68 815,88 8216,84 9037,89
^
y
2
^
yy
2
yy
95,0
89,9037
84,8216
индекс корреляции
91,0
2
R
коэффициент детерминации
3.5. Для обратной регрессии
Расчётная таблица
y x
19,79
0,24 28,40909 1591,2846 2353,22
38,09
0,31 29,5858 1498,7894 912,6441
40,95
0,55 34,48276 1143,6058 748,0225
41,08
0,48 32,89474 1253,5327 740,9284
56,29
0,78 40,98361 746,18535 144,2401
68,51
0,98 49,01961 371,73352 0,0441
75,01
0,94 47,16981 446,48487 45,0241
89,05
1,21 63,29114 25,088686 430,5625
91,13
1,29 70,42254 4,5051557 521,2089
91,26
1,12 56,81818 131,83215 527,1616
99,84
1,29 70,42254 4,5051557 994,7716
108,55
1,49 98,03922 884,42095 1620,063
819,55 10,68 621,54 8101,97 9037,89
^
y
2
^
yy
2
yy
95,0
89,9037
97,8101
индекс корреляции
9,0
2
R
коэффициент детерминации
3.6. Для гиперболической регрессии
Расчётная таблица
8
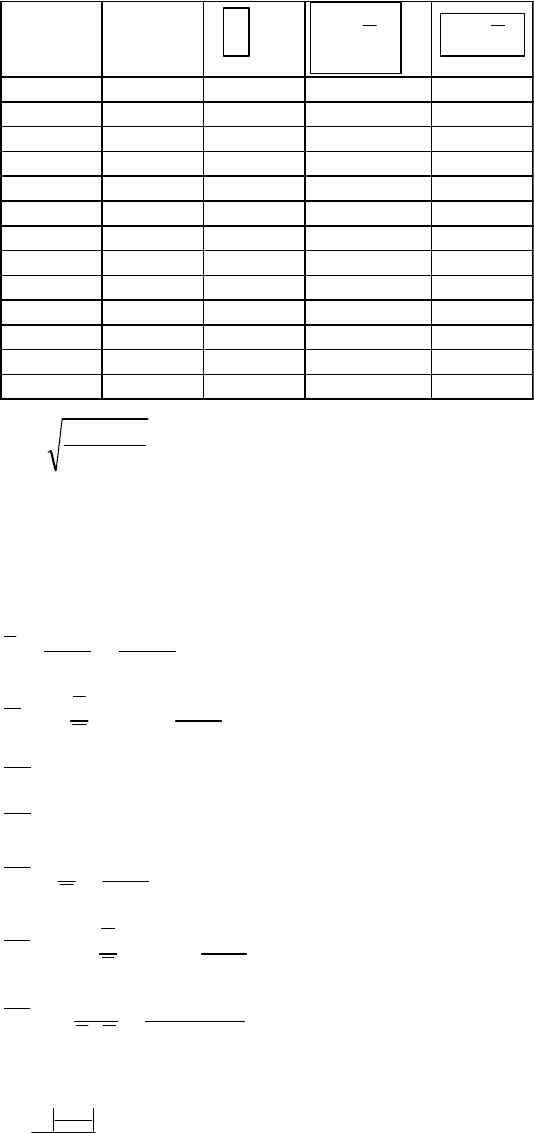
y x
19,79
0,24 8,916667 3526,38028 2353,22
38,09
0,31 30,27419 1445,96196 912,6441
40,95
0,55 62,22727 36,8780165 748,0225
41,08
0,48 56,20833 146,208403 740,9284
56,29
0,78 74,39744 37,1787245 144,2401
68,51
0,98 80,33673 144,882982 0,0441
75,01
0,94 79,35106 122,126012 45,0241
89,05
1,21 84,73967 270,262731 430,5625
91,13
1,29 85,9031 309,869157 521,2089
91,26
1,12 83,23214 222,96889 527,1616
99,84
1,29 85,9031 309,869157 994,7716
108,55
1,49 88,2651 398,605245 1620,063
819,55 10,68 819,75 6971,19 9037,89
^
y
2
^
yy
2
yy
88,0
89,9037
19,6971
индекс корреляции
77,0
2
R
коэффициент детерминации
4. Дать с помощью среднего (общего) коэффициента эластичности сравнительную
оценку силы связи фактора с результатом.
89,0
12
68,10
n
x
x
88,0
3,68
89,0
9,67
1
y
x
aЭ
для линейной функции
8,0
2
bЭ
для степенной функции
18,1
3
bЭ
для экспоненциальной функции
67,0
3,68
7,45
4
y
a
Э
для логарифмической
53,1
89,0
3,68
02,0
5
x
y
aЭ
для обратной функции
37,0
3,6889,0
7,22
6
yx
a
Э
для гиперболической функции
5. Оценить с помощью средней ошибки аппроксимации качество уравнений.
%100
^
n
y
yy
A
Расчётная таблица
9

y x
линейная степенн. экспон.
логарифм.
обратная гипербол.
19,79
0,24 0,222638 0,224517 0,438711 0,273331 0,435528 0,549436
38,09
0,31 0,239984 0,219235 0,18814 0,315386 0,223266 0,205193
40,95
0,55 0,104884 0,148889 0,002376 0,276651 0,15793 0,519592
41,08
0,48 0,014314 0,02708 0,080014 0,121169 0,199252 0,368265
56,29
0,78 0,081222 0,105315 0,043421 0,212388 0,27192 0,321681
68,51
0,98 0,086586 0,090106 0,004843 0,148398 0,28449 0,172628
75,01
0,94 0,043781 0,037003 0,132983 0,023494 0,371153 0,057873
89,05
1,21 0,011331 0,007259 0,004336 0,008295 0,289263 0,048403
91,13
1,29 0,047855 0,021062 0,078572 0,001176 0,22723 0,057357
91,26
1,12 0,080123 0,089383 0,118727 0,071016 0,377403 0,087967
99,84
1,29 0,04356 0,068015 0,015523 0,086166 0,294646 0,139592
108,55
1,49 0,0048 0,038031 0,1465 0,098811 0,096829 0,186871
сумма 0,981076 1,075896 1,254146 1,63628 3,22891 2,714858
ошибка аппроксимации
8,175633 8,9658 10,45121 13,63567 26,90758 22,62382
y
yy
^
6. Оценить с помощью F-критерия Фишера статистическую надёжность результатов
регрессионного моделирования. По значениям характеристик, рассчитанных в пп.
4, 5 и данном пункте, выбрать лучшее уравнение регрессии и дать его обоснование.
Если
,
кр
FF
то уравнение значимо
96,4212;1;05,0
кр
F
2
2
1
2
R
nR
F
функция
R
2
F кометарии
линейная 0,97 323,3333 значимо
степнная 0,86 61,42857 значимо
экспоненцальная 0,98 490 значимо
полулогарифмическая 0,91 101,1111 значимо
обратная 0,9 90 значимо
гиперболическая 0,77 33,47826 значимо
Все данные уравнения являются значимы, но наименьший коэффициент
аппроксимации у линейной функции. Следоваельно будем считать это уравнение
лучшим.
7. Рассчитать прогнозное значение результата, если прогнозное значение фактора
увеличатся на 5% среднего уровня. Определить доверительный интервал прогноза
для уровня значимости 0,05.
05,719,793,0*9,67
93,005,189,0
p
p
y
x
2
2
2
2
^
1
1
1
x
n
x
n
xx
nn
yy
S
p
p
ошибка прогнозирования
10
