Коноваленков В.С., Заборова Т.М. Методичні вказівки та індивідуальні завдання до теми Дослідження поведінки функції за допогою похідних для студентів 1 курсу економічних спеціальностей
Подождите немного. Документ загружается.

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
НАЦИОНАЛЬНА МЕТАЛЛУРГІЙНА АКАДЕМІЯ УКРАЇНИ
МЕТОДИЧНІ ВКАЗІВКИ ТА ІНДИВІДУАЛЬНІ ЗАВДАННЯ
ДО ТЕМИ “ДОСЛІДЖЕННЯ ПОВЕДІНКИ ФУНКЦІЇ ЗА ДОПОМОГОЮ
ПОХІДНИХ ”
З КУРСУ “МАТЕМАТИКА ДЛЯ ЄКОНОМИСТІВ ”
ДЛЯ СТУДЕНТІВ I КУРСУ
ЕКОНОМИЧНИХ СПЕЦІАЛЬНОСТЕЙ
Дніпропетровськ НМетАУ 2009
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
НАЦИОНАЛЬНА МЕТАЛЛУРГІЙНА АКАДЕМІЯ УКРАЇНИ
МЕТОДИЧНІ ВКАЗІВКИ ТА ІНДИВІДУАЛЬНІ ЗАВДАННЯ
ДО ТЕМИ “ДОСЛІДЖЕННЯ ПОВЕДІНКИ ФУНКЦІЇ ЗА ДОПОМОГОЮ
ПОХІДНИХ ”
З КУРСУ “МАТЕМАТИКА ДЛЯ ЄКОНОМИСТІВ ”
ДЛЯ СТУДЕНТІВ I КУРСУ
ЕКОНОМИЧНИХ СПЕЦІАЛЬНОСТЕЙ
ЗАТВЕРДЖЕНО
на засіданні Вченої ради
Протокол № від
Дніпропетровськ НМетАУ 2009
УДК 517.2
Методичні вказівки та індивідуальні завдання до теми “ДОСЛІДЖЕННЯ
ПОВЕДІНКИ ФУНКЦІЇ ЗА ДОПОМОГОЮ ПОХІДНИХ ”З КУРСУ
“МАТЕМАТИКА ДЛЯ ЕКОНОМИСТІВ ”ДЛЯ СТУДЕНТІВ I КУРСУ
ЕКОНОМИЧНИХ СПЕЦІАЛЬНОСТЕЙ / Укл. Коноваленков В.С.,
Заборова Т.М– Дніпропетровськ: НМетАУ, 2009. – с.
Укладачі: В.С.Коноваленков канд. техн. наук
Т.М. Заборова, ст. викладач
Відповідальний за випуск Г.Г.Швачіч, проф.
Редактор: Л.М. Тонкошкур
СОДЕРЖАНИЕ
1. Понятие функции ………………………………………………………………....
2. Характеристики функции………………………………………………………
2.1.Нули функции, знак функции……………………………………………….
2.2.Четность, нечетность функции………………………………………………
2.3.Периодичность функции…………………………………………………….
2.4.Возрастание, убывание (монотонность) функции…………………………
2.5.Экстремум функции…………………………………………………………
2.6.Выпуклость, вогнутость функции………………………………………….
2.7.Асимптоты функции…………………………………………………………
3.Общая схема исследования функции ……………………………………………
4. Индивидуальные задания………………………………………………………..
5.Литература………………………………………………………………………...
1.ПОНЯТТЯ ФУНКЦІЇ
Всякий процесс с количественной стороны характеризуется взаимоизменя-
емостью переменных величин. Такое представление приводит к важнейшему в
математике понятию функциональной зависимости , т.е. связи между перемен-
ными величинами при протекании того или иного процесса , проявлящейся в
этом процессе и характеризующая его.
Определение. Переменную величину y называют функцией
переменной величины x , если каждому значению x из некоторого
множества D по какому-либо правилу поставлено в соответствие одно
определенное значение переменной величины y.
Символически это записывают так:
.),( Dxxfy
Величину x называют независимой переменной (или аргументом); множество
значений x (D) – областью определения функции (D-это множество x, при
которых y не теряет числового смысла).
Например, функция
2 xy
определена для всех X, удовлетворяющих
неравенству
02 x
или
.2x
Таким образом, область определения данной
функции :
;2x
.
Символ
f
указывает совокупность математических действий, которые
необходимо произвести над x, чтобы получить y.
Существуют следующие способы задания функций:
- аналитический (формулой);
- табличный;
- графический (графиком функции в декартовой системе координат
называется множество точек (линия), абсциссами которых являются
значения независимой переменной x , а ординатами - соответствующие
значения функции y).
Как правило, при исследовании функций, эти способы комбинируют.
Из курса общеобразательной школы известны основные элементарные
функции: степенная, показательная, логарифмическая, тригонометрические,
обратные тригонометрические. К элементарным функциям относятся функции,
полученные с помощью арифметических действий над приведенными выше, а
также сложная функция (“функция от функции”, например,
xy sinln
.)
2.ХАРАКТЕРІСТІКИ ФУНКЦІЇ
Изучить функцію - это значит охарактеризовать ее изменение (или, как
говорят, поведение) при изменении независимой переменной x, которая обычно
изменяется непрерывно, возрастая .
2.1.Нули функции, знак функции
Определение. Значение x, при котором функция y обращается в нуль,
называется нулем функции, т.е.
0
xx
-нуль функции
)(xfy
, если
0)(
0
xf
.
При положительном знаке функции в некотором интервале оси OX
график функции расположен выше оси ОХ; при отрицательном- ниже. В
нуле функции график имеет общую точку с осью ОХ (рис.1).
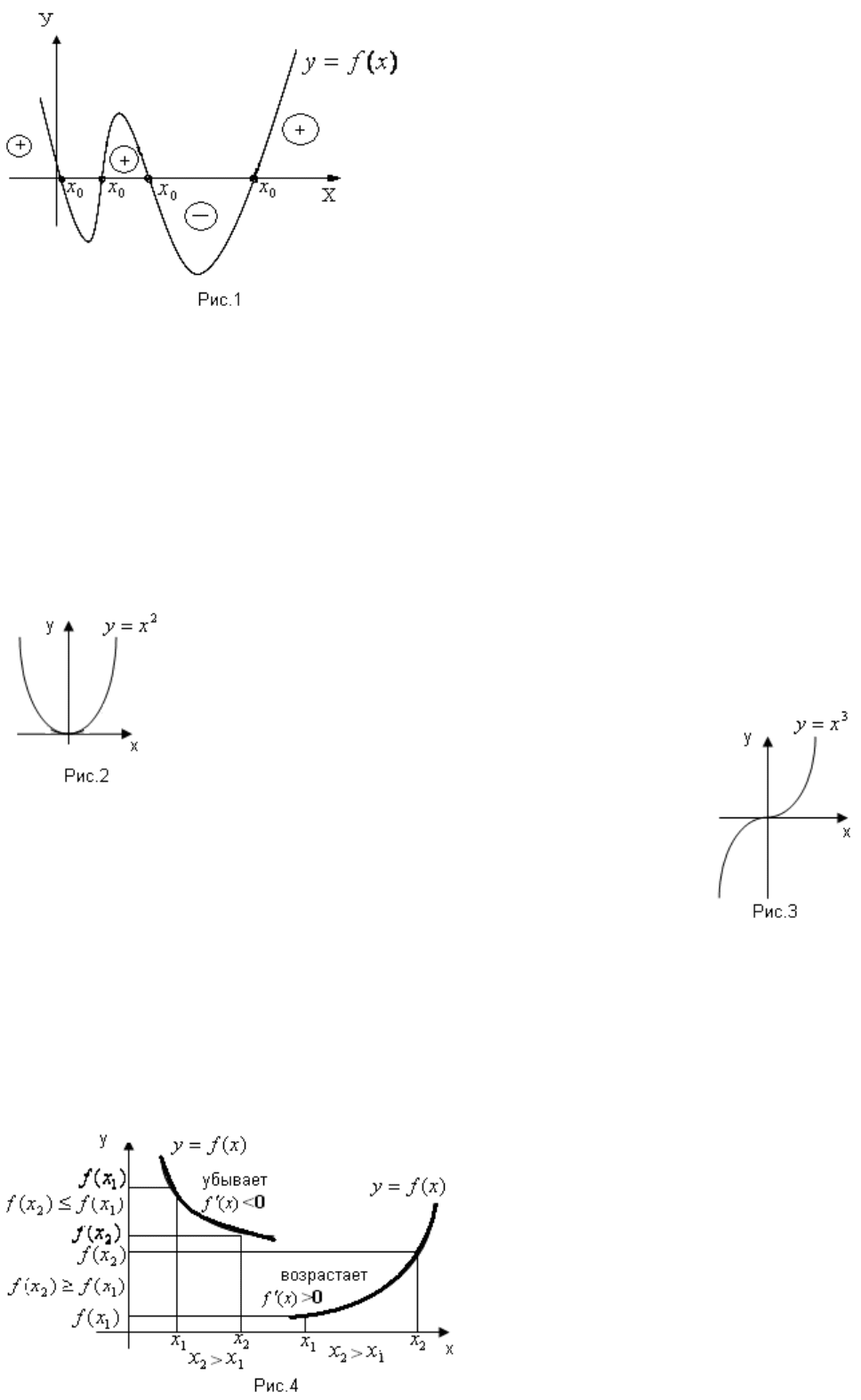
2.2.Четность, нечетность функции
Определение. Функция
)(xfy
называется четной , если изменение
знака у любого значения аргумента x
не влечет за собой изменение
функции , т.е.
).()( xfxf
Функция
)(xfy
называется нечетной, если изменение знака у любого
значения аргумента x влечет за собой изменение знака функции
(абсолютная величина значения функции остается без изменения), т.е.
).()( xfxf
Пример 1.Функция
.)(
2
xxfy
Находим
).()()(
22
xfxxxf
Таким
образом функция
2
xy
является четной (Рис.2).
Пример 2. Функция
.)(
3
xxfy
Находим
).()1()()(
333
xfxxxf
Таким образом функция
3
xy
является нечетной (рис.3).
Из рисунков видно, что график четной
функции симметричен относительно оси ОУ,
график нечетной функции симметричен
относительно начала координат.
Если условия четности и нечетности не выполняются, то
функция не является ни четной ни нечетной. График такой
функции симметрией не обладает.
2.3.Периодичность функции
Определение. Функция
)(xfy
называется периодической, если
существует положительное число Т, для которого при любом значении х
справедливо следующее равенство:
).()( xfTxf
Наименьшее
положительное число Т называется периодом функции.
К числу периодических функций относятся тригонометрические функции
).(,);2(cos,sin
TctgxytgxyTxyxy
2.4.Возрастание, убывание (монотонность) функции
Определение. Функция
)(xfy
называется возрастающей
(убывающей) на некотором
интервале, если большим
значениям аргумента
соответствуют большие
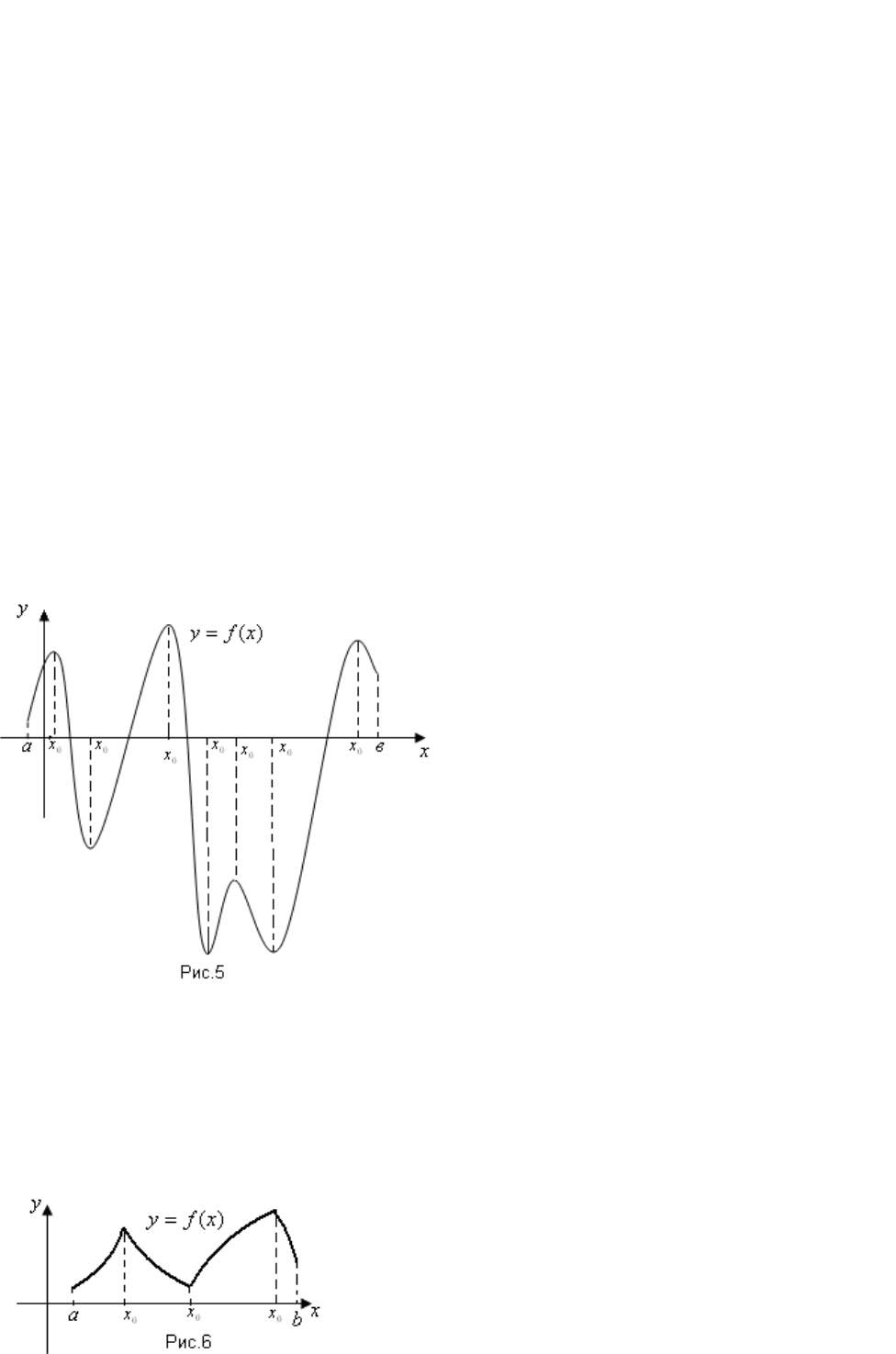
(меньшие) значения функции :
2
x
>
1
x
и
)()(
12
xfxf
,то функция
)(xfy
-
возрастает;
2
x
>
1
x
и
)()(
12
xfxf
, то функция
)(xfy
- убывает (рис.4).
Интервал значений x, в котором функция возрастает (убывает),
называется интервалом монотонности (возрастания (убывания)) функции.
Исследование вопроса о монотонности функции, исходя из определения,
весьма затруднительно. Однако существует связь между монотонностью
функции на некотором интервале и свойствами производной этой функции на
данном интервале. Эта связь определяется признаками монотонности функции.
1.Необходимый признак монотонности.
Если дифференцируемая функция
)(xfy
возрастает (убывает) на
некотором интервале, то производная этой функции неотрицательная
(неположительная) на этом интервале, т.е.:
.,)0)((0)( baxxfxf
2.Достаточный признак монотонности.
Если функция
)(xfy
непрерывна на некотором интервале,
дифференцируема во всех внутренних точках этого интервала и
)(xf
>0
bax ,
(
)(xf
<0
bax ,
), то функция возрастает (убывает) на этом
интервале (рис.4).
Следует подчеркнуть, что производная монотонной функции в отдельных
точках интервала может обращаться в нуль:
)(xf
=0. Такие точки
называются стационарными или
критическими точками (см. ниже).
2.5.Экстремум функции
Особую роль при исследовании
функции играют значения х,
отделяющие интервалы возрастания от
интервалов убывания и наоборот, т.к. в
этих точках функция
)(xfy
меняет
характер своего поведения.
Определение. Точка
0
x
называется
точкой максимума (минимума)
функции
)(xfy
, если
)(
0
xf
-
наибольшее (наименьшее) значение
функции
)(xfy
в некоторой
окрестности точки
0
x
.
Функция на заданном интервале может иметь несколько экстремумов
(максимумов и минимумов),причем минимум может быть больше максимума
(рис.5).Поэтому различают экстремумы, имеющие относительный характер
(локальный экстремум) и наибольшее и наименьшее значение функции на
интервале - абсолютный максимум и минимум.
Замечание. Следует отметить, что экстремумы
могут иметь вид, изображенный на рис.6.

Точки экстремумов такого вида находятся среди тех точек области
определения, в которых функция
)(xfy
не имеет производной.
Теперь определим необходимое условие существования экстремума.
Если функция
)(xfy
,непрерывная на некотором интервале и
дифференцируемая во всех внутренних точках этого интервала, в точке
0
x
достигает экстремума, то ее производная в этой точке равна нулю, т.е.
.0)(
xf
Следует еще раз подчеркнуть, то данное условие является необходимым, т.е.
0)(
xf
еще не означает ,что
0
x
- точка экстремума. Поэтому эти точки еще
называют точками возможного экстремума.
Вернемся к функции
3
)( xxfy
, изображенной на рис.3.
0)(,3)(
2
xfxxfy
при
,0x
однако, точка
0x
не есть точка экстремума
(см. рис.3).
Сформулируем теперь достаточные условия существования экстремума.
Первый достаточный признак экстремума.
Точка
0
x
является точкой экстремума функции
)(xfy
, если при
переходе значения аргумента х через
0
x
производная функции
)(xf
меняет
знак (с “+” на “-“ –точка
0
x
является точкой максимума; с ”-“ на “+”-
точкой минимума ).
Замечание. Следует иметь в виду, что в самой точке
0
x
функция
)(xfy
должна быть обязательно непрерывна. В противном случае производная
функции может менять знак при переходе х через
0
x
, но
0
x
не будет точкой
экстремума.
Например
2
1
x
y
.
.
2
3
x
y
При x<0
y
<0, а при x>0,
y
>0,
Однако точка x=0 не является точкой экстремума ( в точке
x=0 функция
2
1
x
y
имеет бесконечный разрыв).
Второй достаточный признак экстремума.
Точка
0
x
является точкой экстремума функции
)(xfy
, если
,0)(
0
xf
а
,0)(
0
xf
причем, если
,0)(
0
xf
то
0
x
является точкой минимума, если
,0)(
0
xf
то
0
x
является точкой максимума.
Например,
.2
2
xxy
102222 xxxy
точка
возможного экстремума.
2
y
>0- точка x=-1 -точка
минимума.
Приведем одну из возможных схем исследования
функции на экстремум, отыскания наибольшего и
наименьшего значения функции, непрерывной на
некотором интервале:
1.Находим производную
).(xf
2.Находим точки возможного экстремума; для этого:
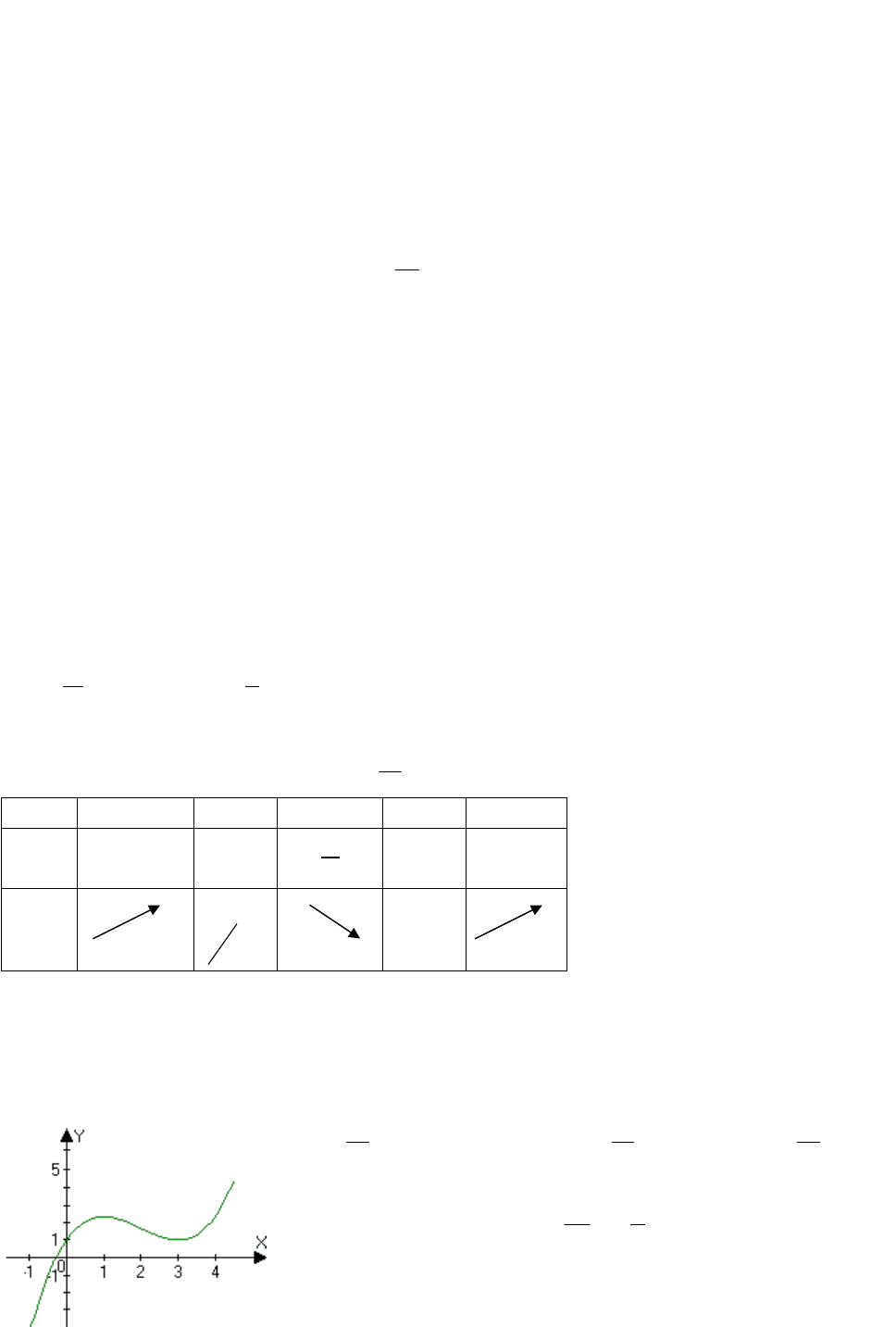
а) приравниваем производную нулю и находим действительные корни
уравнения
;0)(
xf
б) находим значения х , в которых
)(xf
терпит разрыв.
3.Исследуем знак производной слева и справа от точек возможного экстремума
(т.к. знак производной остается постоянным между двумя критическими
точками, то достаточно определить знак производной в любой точке,
расположенной между ближайшими критическими точками).
4.Вычисляем значения функции
)(xfy
при каждом критическом значении
аргумента.
Получаемую информацию удобно оформлять в виде таблицы.
Пример. Исследовать функцию
132
3
2
3
xx
x
y
на наличие экстремумов.
Найти наибольшее и наименьшее значение на интервале
.5,0
Рассматриваемая функция определена на всей числовой оси.
1.
.34
2
xxy
2.а)
.3,1034
21
2
xxxxy
б) производная функции не терпит разрыва ни в одной точке из области
определения.
Строим таблицу:
3)0(
y
>0- функция возрастает на интервале
)1,(
.
13242)2(
2
y
<0- функция убывает на интервале
)3,1(
.
Таким образом, в точке
1x
выполняется первое достаточное условие
существования экстремума и точка
1x
является точкой максимума и он
равен
.
3
7
11312
3
1
)1(
2
3
y
33444)4(
2
y
>0- функция возрастает на интервале
),3(
и точка
3x
является точкой минимума:
.111332
3
3
)3(
2
3
y
.
x
)1,(
1x
)3,1(
3x
),3(
)(xf
+ 0 0 +
)(xf
max
3
7
min
1
После того как экстремальные значения функции найдены легко найти
наибольшее и наименьшее значения функции в интервале
.5,0
Для этого необходимо сравнить значения функции
)(xfy
в экстремальных
точках и на концах интервала:
.110302
3
0
)0(
2
3
y
.
3
23
15352
3
5
)5(
2
3
y
Таким образом, наименьшее значение функции равно
единице, а наибольшее -
.
3
2
7
3
23
2.6.Выпуклость, вогнутость функции
Определение. Кривая
)(xfy
называется выпуклой
вогнутой) на некотором интервале
),( ba
,если все точки кривой лежат ниже
(выше) любой касательной к этой кривой на данной интервале.
Выпуклость, вогнутость кривой являются важной характеристикой ее формы.
Исследование выпуклости, вогнутости функции на некотором на основе
определения можно заменить исследованием более простого вопроса о знаке
производной второго порядка на этом интервале.
Теорема. Если во всех точках интервала
),( ba
производная второго
порядка отрицательна (положительна), т.е.
)(xf
<0 (
)(xf
>0), то кривая
)(xfy
выпуклая (вогнутая) на этом интервале.
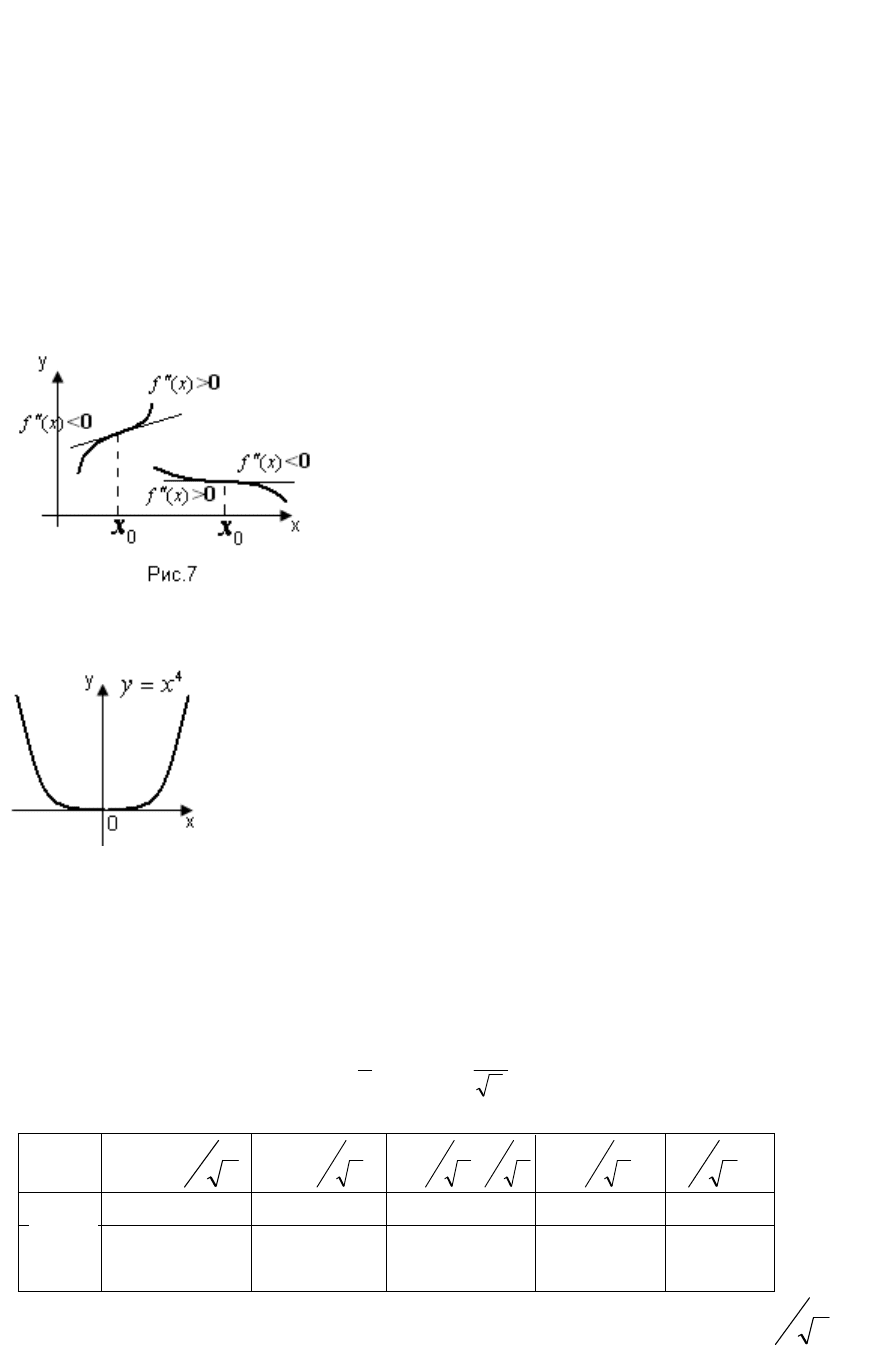
Определение. Точка, отделяющая выпуклую
часть непрерывной кривой от вогнутой части (и
наоборот), называется точкой перегиба.
Очевидно, что в самой точке перегиба касательная
пересекает кривую (если эта касательная
существует) (рис.7).
Из определения точки перегиба следует, что в
точке
0
x
0)(
0
xf
- необходимое условие
существования точки перегиба. Точки, в которых выполняется необходимое
условие, называются точками возможного перегиба.
Например, функция
00;124
0
234
xyxyxyxy
-
точка, в которой выполняется необходимое условие, однако
перегиба в этой точке нет.
Достаточное условие существования точки перегиба.
Точка
))((
0,0
xfx
есть точка перегиба линии
)(xfy
, если
)(xf
меняет знак при переходе
x
через
0
x
(с “+” на “-“ –
слева от точки
0
x
имеем выпуклый участок, справа - вогнутый; с”-“ на
“+”- наоборот (рис.7)).
Пример. Найти точки перегиба и определить интервалы выпуклости и
вогнутости кривой
.
2
x
ey
.0)24()2(222
2
2222
xeexxeyexy
xxxx
Откуда имеем
.2
1
2
1
024
2,1
22
xxx
Полученную информацию удобно оформлять в виде таблицы:
x
)
2
1
,(
2
1
x
)
2
1
,
2
1
(
2
1
x
),
2
1
(
)(xf
+ 0 - 0 +
)(xf
Точка
перегиба
Точка
перегиба
,0)1(
f
следовательно, функция вогнутая на интервале
)
2
1
,(
,
