Конахович Г.Ф., Климчук В.П., Паук С.М., Потапов В.Г. Защита информации в телекоммуникационных системах

Подождите немного. Документ загружается.

200

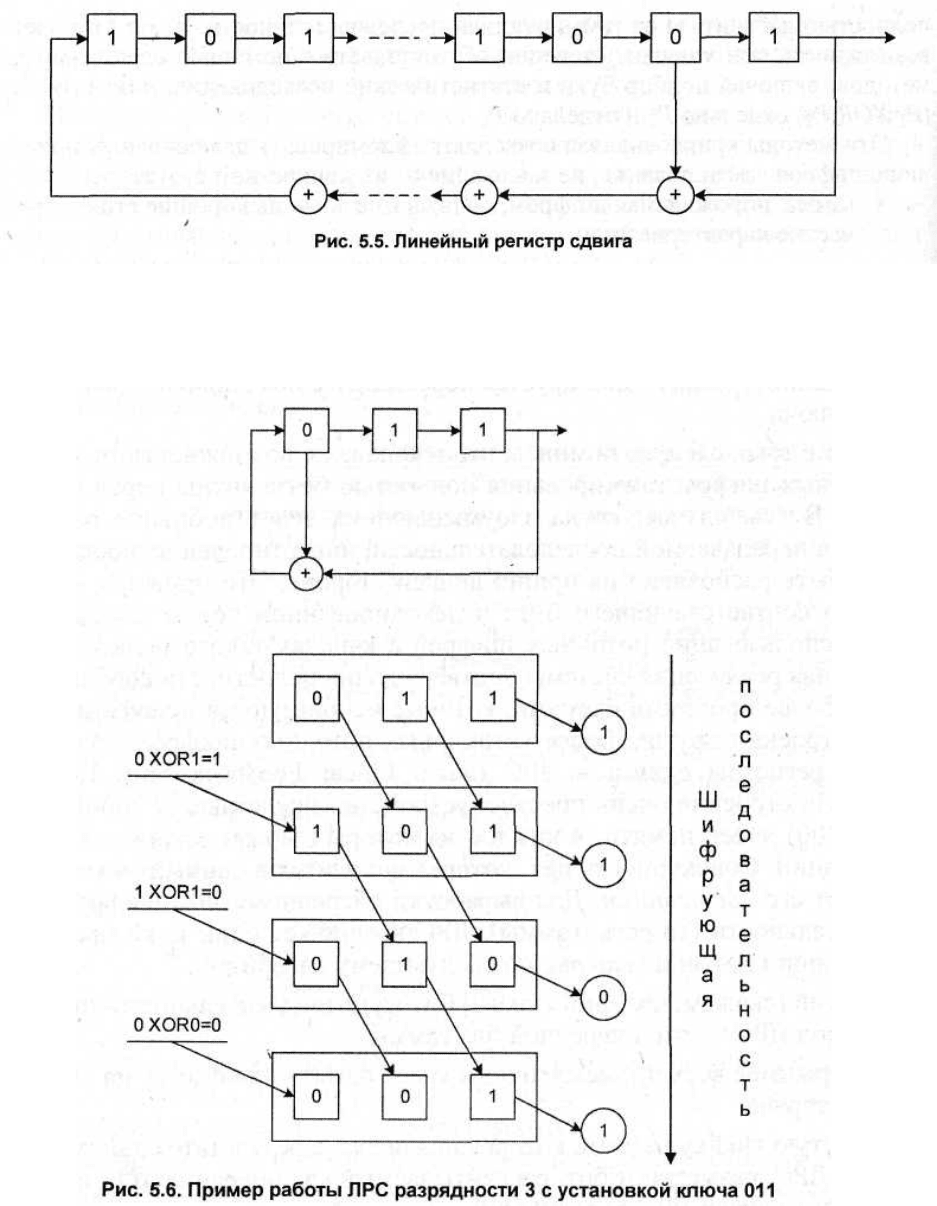
Пример работы ЛРС разрядности 3 с установкой ключа 011 показан на рис.

5.6.

Если скремблер работает достаточно долго, то обязательно возникает его

зацикливание, потому что количество возможных вариантов состояния ЛРС

конечное и, как следствие, после выполнения определенного количества тактов в

его ячейках образуется комбинация бит, которая уже была создана ранее. С этого

момента кодирующая последовательность начнет циклически повторяться с

фиксированным периодом.

201

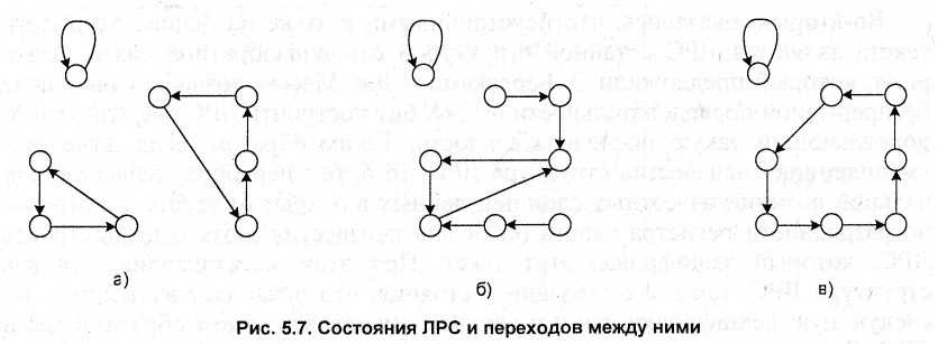
Если представить множество состояний ЛРС и переходов между ними в виде

графа, то, в зависимости от номера ячеек, порождающих обратную связь, могут

образоваться совсем разные топологии. Некоторые из них представлены на рис.

5.7.

Цикл "000" характерен для всех графов вследствие строения ЛРС. На рис. 5.7

а) мы видим, кроме "нулевого" цикла, еще два: 3-х и 4-х состояний. На рис. 5.7

б) цепочка сходится к циклу 3-х этапов и уже никогда оттуда не выходит. И,

наконец, на рис. 5.7 в) все возможные состояния, кроме нулевого, объединены в

один замкнутый цикл.

Очевидно, что как раз в этом случае, когда все 2

-1 состояний системы (где N

— разрядность ЛРС), кроме нулевого, образуют единый цикл, период

повторения гаммы максимальный, а корреляция между длиной цикла и на-

чальным состоянием регистра (то есть, ключом), которая привела к появлению

более слабых ключей, отсутствует [16].

Схемы с выбранными по данному закону обратными связями называют

генераторами последовательностей наибольшей длины (ПНД). Существует

большое количество публикаций с рекомендациями относительно таблиц

номеров ячеек, от которых необходимо выбрать отводы обратной связи для

получения ПНД. В целом проблема порождения последовательностей наи-

большей длины на ЛРС тесно связана с математическим понятием неприво-

димых и примитивных полиномов над полем Галуа GF(2). [16]

Основной помехой для применения ЛРС в качестве непосредственно шифров

является их неспособность противостоять атаке по известному открытому

тексту. Во-первых, когда злоумышленнику известна структура обратных связей

ЛРС разрядности N и хотя бы N последовательных бит, порожденных им на

любом этапе шифрования (то есть, состояние регистра (N-1) тактов назад), то все

последующие состояния регистра могут быть получены самостоятельно. Таким

образом, будет порождена вся последующая за этим моментом гамма, и весь

текст дешифрован.

Более того, восстановление битов гаммы возможно и в обратном направлении

вследствие строения ЛРС. Это позволяет злоумышленнику записывать весь

передаваемый шифротекст и одновременно выполнять попытки подобрать

соответствующий ему открытий текст на основе набора высоковероятных для

202

данного контекста фраз или данных. Если в любой момент времени открытий

текст длиной N будет успешно подобран, то и весь шифрованный поток,

следующий за ним, будет успешно дешифрован. Параллельно (возможно, на

другой ЭВМ) весь законспектированный до точки взлома шифротекст будет

прочитан в обратном направлении.

Во-вторых, оказалось, что неустойчивыми к атаке на основе открытого текста

являются ЛРС с тайной структурой отводов обратной связи. Алгоритм, который

предложили Э. Берлекамп и Дж. Месси, позволяет на основе беспрерывной

последовательности из 2xN бит построить ЛРС разрядности N, порождающий

такую последовательность. Таким образом, если даже злоумышленнику

неизвестна структура ЛРС, то путем перебора сначала из начальной позиции

известных слов или данных в открытом тексте, а потом — по разрядности

регистра сдвига (если она неизвестна) возможно построить ЛРС, который

зашифровал этот текст. При этом восстанавливается как структура ЛРС, так и

его текущие состояния, что позволяет выполнить последующую дешифровку,

как и в случае с известным видом обратной связи ЛРС. Для устранения этих

недостатков были созданы нелинейные поточные шифры. [16]

Наиболее популярны на сегодняшний день комбинирующие, фильтрующие и

динамические поточные шифры. Все они в качестве базовых элементов

используют линейные регистры сдвига — при этом только те, которые

порождают последовательности наибольшей длины. Во всех трех методах

основной целью ставится получение большого периода порождаемой гаммы,

высокой нелинейности, устойчивости к атакам по открытому тексту и корре-

ляционным атакам.

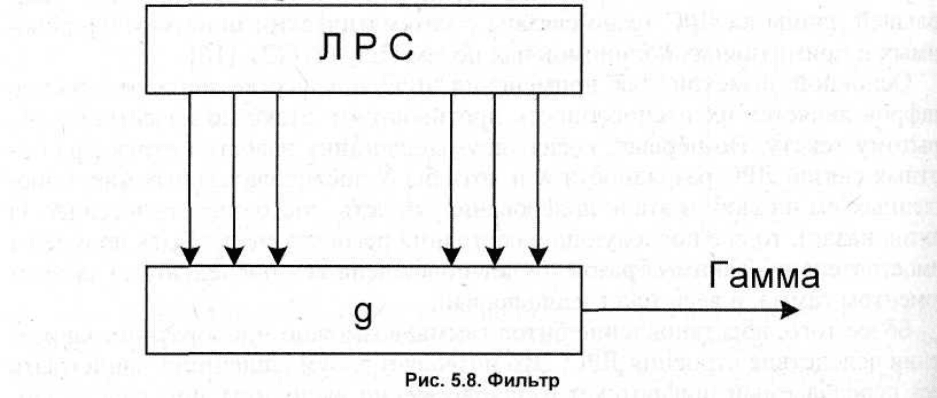
Фильтрующие шифры имеют наиболее простую структуру из нелинейных

поточных шифров. Их строят на базе одного ЛРС путем создания от его ячеек

дополнительных отводов, никак не связанных с отводами обратной связи.

Значения, получаемые по этим отводам, уменьшают на основе некоторой

нелинейной функции — фильтра (рис. 5.8). Бит — результат этой функции —

подают на выход схемы как очередной бит гаммы.

203

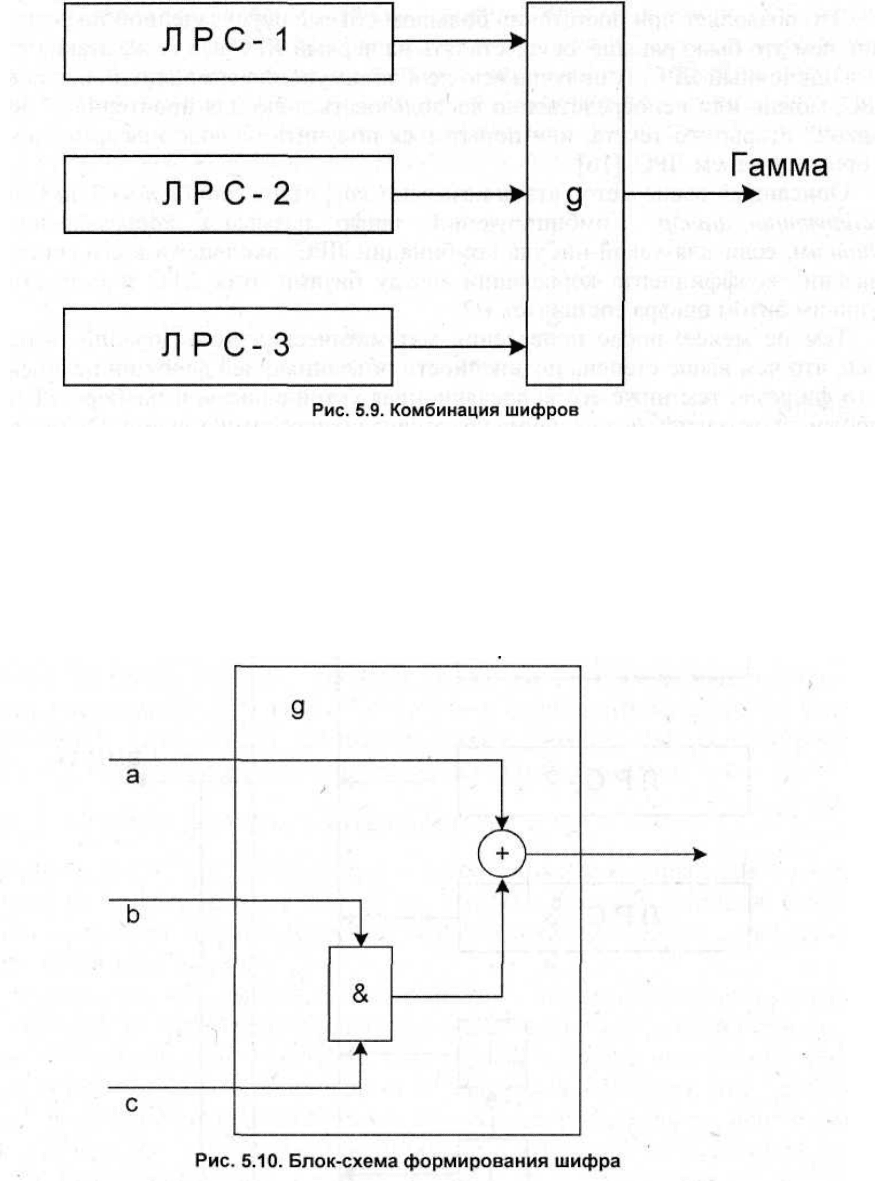
Комбинирующие шифры строятся на основе нескольких ЛРС, объединяя

нелинейной функцией биты, порождаемые каждым из них на очередном шаге

(рис. 5.9).

Одной из основных проблем комбинирующих шифров является возможность

утечки информации из одного или нескольких ЛРС в выходную гамму. Так, в

простейшем случае, представленном на рис. 5.10, итоговая шифрующая

последовательность порождается по формуле

g = а

⊕

(b & с)

Несмотря на то, что такая гамма является сбалансированной (то есть, ве-

роятность появления "О" и "1" в ней совпадают), в нее с недопустимо большой

вероятностью проходит поток битов, порожденный первым ЛРС. Действительно,

вероятность

204

P(g=6) = 4/8=l/2, P(g = c) = 4/8 = l/2,

однако

P(g = a) = 6/8

Это позволяет при достаточно большом объеме перехваченной информации,

чем это было раньше, осуществлять на первый ЛРС все те же атаки, что и на

одиночный ЛРС. А получив всю необходимую информацию по первому ЛРС,

можно или непосредственно воспользоваться ею для прочтения с "догадкой"

открытого текста, или попытаться получить больше информации о втором и

третьем ЛРС. [16]

Описанный выше метод атаки называют корреляционной атакой на ком-

бинирующий шифр. Комбинирующий шифр называют корреляционно-стойким,

если для какой-нибудь комбинации ЛРС, входящего в его состав, значение

коэффициента корреляции между битами этих ЛРС и результирующим битом

шифра составляет 1/2.

Тем не менее, после проведения математических исследований оказалось, что

чем выше степень нелинейности объединяющей функции нелинейного фильтра,

тем ниже его корреляционная устойчивость, и наоборот. Разработчики оказались

между двумя криптоаналитическими атаками. Одним из методов выхода из этой

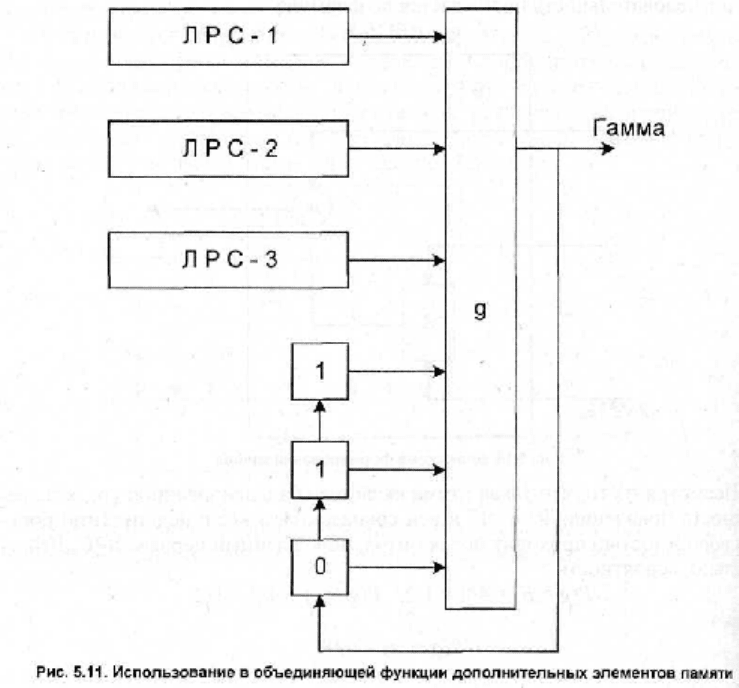
ситуации является использование в объединяющей функции дополнительных

элементов памяти. Такие ячейки хранят несколько бит, характеризующих

предварительные состояния функции, и смешивают их с этой же функцией на

этапе вычислений (рис. 5.11).

205

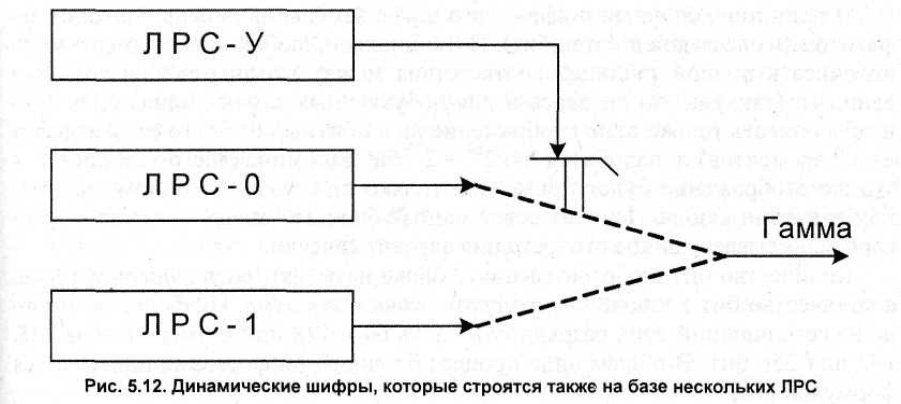
Динамические шифры строятся также на базе нескольких ЛРС, однако

объединяют их не на равных основаниях, а по схеме "начальник-подчиненный".

Так, например, в схеме, представленной на рис. 5.12, бит, порождаемый

управляющим регистром, определяет, бит какого из подчиненных ЛРС (первого

или второго) будет подан на выход всего алгоритма. Бит из регистра,

противоположного выбранному, отбрасывается.

По другой схеме, если на очередном шаге управляющий ЛРС генерирует "1",

то бит подчиненного ЛРС на этом же шаге поступает на выход системы, а если

управляющий ЛРС выдал "О", то бит подчиненного регистра просто

отбрасывается. Конечно же, возможны и более сложные схемы взаимодействия

ЛРС и их комбинаций с вышеперечисленными методами.

5.3.2. Основы блочного шифрования

Отличительной чертой блочных шифров является обработка исходной

информации по несколько (десятков, сотен) бит, то есть, поблочная. Блочные

шифры — это логичное продолжение идеи алфавитных замен, перенесенной в

новое "цифровое" время.

Очевидно, что при выполнении алфавитных подстановок двухбуквенных пар

(биграмм) на другие двухбуквенные пары, частотный анализ становится уже

достаточно сложной задачей. В том случае, когда по некоторому закону

изменяются наборы из 4, 8 или даже 16 символов, ни про какое частотное

раскрытие шифров речи идти не может — объем шифротекста, необходимого

для такой атаки, растет экспоненциально. Проблема, из-за которой такие схемы

не были применены раньше, заключалась в отсутствии надежного и простого в

применении алгоритма преобразований, который, в идеале, к тому же, зависит

только от ключа шифрования. [16]

Все изменила электроника. В современных системах обработки, передачи и

хранения информации двоичное представление данных позволило достичь

206

небывалой абстракции формы от содержания. Любой информационный поток

может быть представлен в виде набора унифицированных знаков — битов, а

вычислительные машины позволили разработать совсем другие законы

модификации данных.

Любой блочный шифр в общем виде представляет собой закон отображения

множества входных блоков исходного текста на множество блоков

зашифрованного текста. Кроме того, этот закон очень сильно зависит от тайного

ключа шифрования.

В принципе, блочный шифр — это шифр замены над очень большим ал-

фавитом (из десятков и сотен бит). Потенциально, любой шифр замены можно

описать полной таблицей соответствия между входными и выходными данными

(так, как это делалось и для побуквенных замен), однако для того чтобы описать

только одно отображение на 64-битный блок (то есть, алфавит из 2

элементов)

понадобится 64х2

— 2

бит запоминающего устройства, а это же отображение

будет применено только при каком-то одном конкретном значении ключа.

Поэтому современный блочный шифр — это закон, который описывает данное

отображения алгоритмически.

Количество бит в обрабатываемом блоке называют разрядностью блока, а

количество бит в ключе — размером ключа алгоритма. Наиболее популярна на

сегодняшний день разрядность блока 64 и 128 при размере ключа 128, 192 или

256 бит. В общем виде процесс блочного шифрования описывается формулой

[16]

Z = EnCrypt(x, key)

где х — блок исходного текста, Z — зашифрованный блок, key — ключ шиф-

рования. Разрядность зашифрованного блока в классических блочных шифрах

совпадает с разрядностью исходного блока, поэтому за этап шифрования поток

данных не уменьшается и не увеличивается в размерах. Дешифрование

описывается соответственно формулой

Х= DeCrypt(Z, key)

В тех случаях, когда и для шифрования, и для дешифрования используется

одна и та же последовательность действий, то есть

EnCrypt = DeCrypt = Crypt

и, соответственно,

Crypt(Crypt(X, key), key) = X

блочный шифр называют абсолютно симметричным. Такие шифры имеют

как преимущества, так и недостатки.

Основной идеей почти всех блочных шифров является тот факт, что по-

следовательность битов любой длины Q можно представить в виде натурального

числа в диапазоне [0...

-1]. Более того, один и тот же объем данных, разбивая

его разными способами на подобные блоки, можно представить как в виде

большого набора небольших чисел (например, от 0 до 15 или от 0 до 255), так и в

виде нескольких чисел (например, диапазона [0...4294967295]). Тут все зависит

от схемы разбиения потока данных на блоки битов. Таким образом, над этими

натуральными числами и выполняются множество простых математических и

207

алгоритмических преобразований — так называемых криптопримитивов — из

числа тех, которые легко выполняются на современных ЭВМ.

Для криптопреобразований нет никакой разницы, имеет обрабатываемая

группа битов (число) какой-либо смысл или нет. Например, на некотором

промежуточном этапе в обрабатываемом 8-битном блоке первые два бита могут

быть взяты из третей буквы шифруемого текста, следующие три — из шестой, а

последние три бита вычислены на основе первой и пятой буквы. Главное, чтобы

после установки на принимающей стороне все биты в блоке заняли свои

правильные места и получили правильное значение, то есть, опять были

преобразованы в текст, имеющий смысл. В таком абстрагировании от смысловой

нагрузки на промежуточных стадиях и заключена сила двоичного представления

данных.

Несомненно, для однозначного дешифрования текста на принимающей

стороне все использованные преобразования должны быть обратимыми. Ни на

одном из этапов шифрования в обрабатываемой последовательности не должна

возникнуть потеря информации.

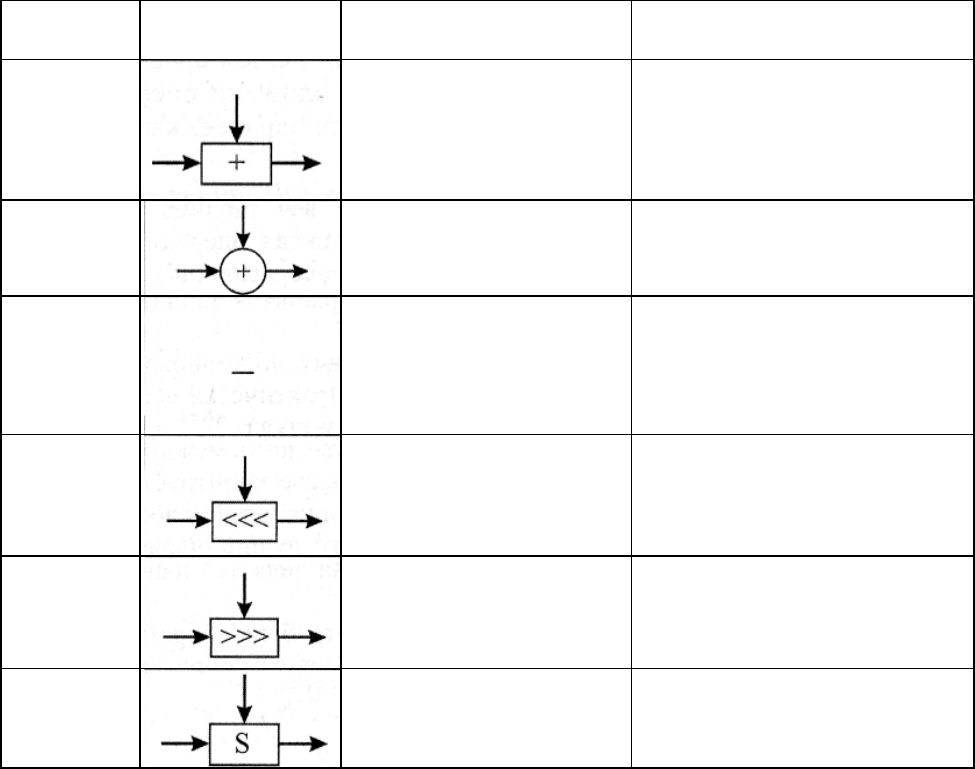
Перечень наиболее приемлемых преобразований и их условные обозначения

на схемах представлен в табл. 5.2.

Таблица 5.2. Наиболее приемлемые преобразования и их условные обозначения на схемах

Операция

Условные

обозначения

Математическая

нотация

Примечание

Сложение

X' = X + V

В случае переполнения резуль-

татом разрядности операндов, бит

переноса отбрасывается, потери

информации при этом не

происходит

Исклю-

чающее

ИЛИ

X' = X®V

Операция обратна сама себе

Умножение по

модулю 2

X' = (X*V)mod(2

+1)

Это преобразование обратимо

Множитель по известному про-

изведению и другому множителю

определяется по

алгоритму

Эвклида

Циклический

битовый

сдвиг влево

X' = X ROL V

Операция является обра

тной

циклическому сдвигу вправо

Циклический

битовый

сдвиг вправо

X' = X ROR V

Операция является обратной

циклическому сдвигу влево

Табличная

подстановка

X' = S - Box[X]

208

Несколько слов о табличных подстановках, занимающих отдельное место в

криптографических преобразованиях... С помощью табличных подстановок

(англ. "Substitute-box-S-box") реализуют наиболее общие законы изменения

данных, которые часто не воспроизводятся ни аналитически, ни алгоритмически.

В тех случаях, когда в шифрующем алгоритме необходимо реализовать

функцию, которая достаточно сложна для микропроцессора или вообще не

описывается алгоритмом, наиболее приемлемым решением является занесение

ее значения в массив, хранимый в постоянной или оперативной памяти. Такое

задание функции называют табличным.

Количество битов в исходном операнде называют разрядностью входа

табличной подстановки, количество битов в результате — разрядностью выхода.

В большинстве случаев табличные подстановки используются в качестве

биэктивной (однозначно обратимой) функции — в этом случае разрядность

входа и выхода совпадают. Чаще всего по такой схеме используются

подстановки 4x4 (четыре на четыре) бита, 8x8 бит.

Обратное преобразование (S - Вох

-1

), если в нем есть необходимость, задают

дешифрующей стороне также таблицей такого же размера. В том случае, когда

от подстановок не требуют обратимости, вместе с традиционными применяются

подстановки 4x8, 8x32 и некоторые другие.

Запись функции в таблице имеет свои преимущества и недостатки. В

сравнении с долгим вычислением функции, выборка из таблицы выполняется

значительно быстрее, однако эти две операции нельзя сравнить по скорости с

обычным сложением или XOR, потому что одним из операндов в выборке всегда

является ячейка памяти, и предвидеть заранее, какая из ячеек потребуется,

невозможно.

По этой причине на современных процессорах табличная выборка вы-

полняется довольно быстро только тогда, когда вся таблица размещена в кэш-

памяти процессора. В противном случае каждая операция выборки инициирует

многотактовый процесс обращения к оперативной памяти. Все это накладывает

жесткие ограничения на размер хранимой таблицы и, соответственно, на

разрядность ее входа и выхода.

Одним из неоспоримых преимуществ табличных подстановок является

скорость в отношении к нелинейным операциям. Практически все представ-

ленные в табл. 5.2 операции, кроме умножения по модулю 2

N+1

и табличных

подстановок, имеют очень высокую линейную зависимость между входными и

выходными значениями, а это очень плохо в смысле криптоустойчивости шифра

к линейному криптоанализу. Для повышения устойчивости шифра к этому

классу атак табличная подстановка намного лучше операции умножения по

модулю 2

N+1

, и на сегодняшний день она является наиболее приемлемым

нелинейным преобразованием.

В тех случаях, когда от преобразований не требуют обратимости по входным

параметрам, в дополнение к вышеперечисленным обратимым функциям

используются операции, представленные в табл. 5.3.

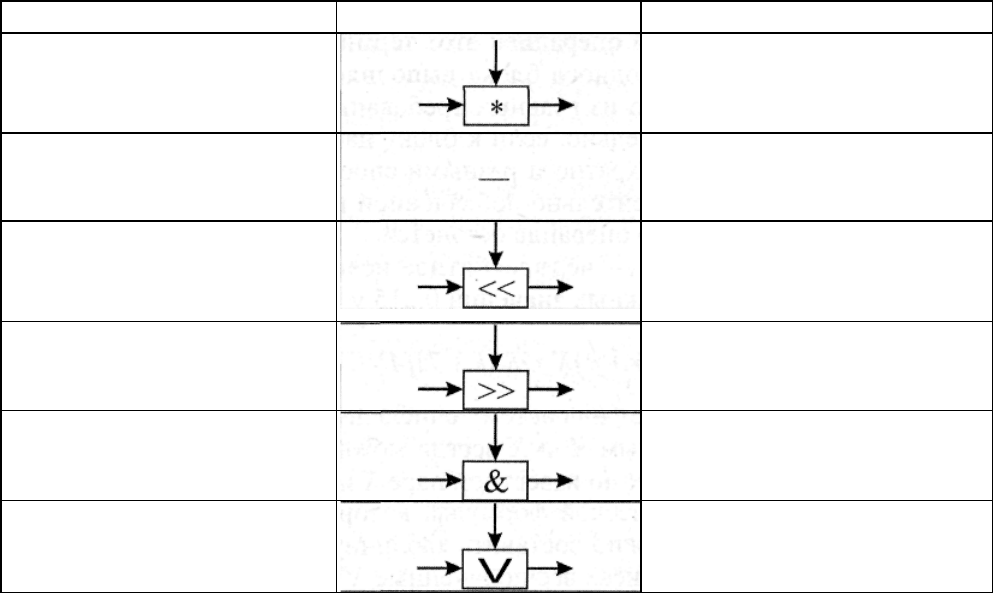
209

Таблица 5.3. Основные необратимые криптопримитивы

Операция Условные обозначения Математическая нотация

Умножение X' = {X·V)mod(2

)

Остаток (модуль) отделения

X' = X mod V

Арифметический битовый сдвиг

влево

X' = X SHL V

Арифметический битовый сдвиг

вправо

Х' = Х SHR V

Логическое "И" Х' = Х AND V

Логическое "ИЛИ" X'= X OR V

Покажем, что может выступать в качестве параметров V в обратимых и

необратимых операциях. Во-первых, это фиксированные числовые константы.

Единственным ограничением, которым всегда пользуются проектировщики

блочных шифров, является логическое обоснование их выбора. В тех случаях,

когда шифр полон фиксированных числовых констант, выбор которых тяжело

пояснить, может возникнуть подозрение, что разработчики планомерно

конструировали их для получения каких-то недокументированных возможностей

по раскрытию шифра. Поэтому, когда применение фиксированных числовых

констант выполняет только роль "перемешивания" данных, их обычно выбирают

из двоичной записи общеизвестных, не связанных ни с чем величин, например,

чисел π, е или φ (золотое сечение), или как контрольную сумму какого-нибудь

распространенного текста.

Другим возможным значением параметра V является материал ключа.

Материалом ключа называют блок данных, вычисленный на основе ключа

шифрования, который зависит только от этого ключа. В простейшем случае

материалом ключа может быть сам ключ (если его разрядность совпадает с

разрядностью операций) или произвольная его часть без какой-либо обработки.

Однако прямое применение ключа в преобразованиях может привести к

раскрытию некоторой информации о нем, например, при большом количестве

известных пар "открытий текст/зашифрованный текст" И хотя вероятность такой

атаки очень мала, необходимо перестраховаться. Для этого в качестве материла

ключа используют значения, вычисленные из него по необратимой схеме. При

этом лучше всего, чтобы любой элемент материала зависел от всех битов ключа,