Конахович Г.Ф., Климчук В.П., Паук С.М., Потапов В.Г. Защита информации в телекоммуникационных системах

Подождите немного. Документ загружается.

190

К сожалению, большинство нелинейных радиолокаторов работают на

фиксированных частотах без возможности перестройки, а это ухудшает их

эксплуатационные характеристики. Вообще, более удобны в эксплуатации

локаторы, имеющие возможность перестройки в границах какого-либо диа-

пазона. Например, локатор Orion (NJE-400) обеспечивает автоматический режим

выбора рабочей частоты в диапазоне 880-1000 МГц. Ее оптимальное значение

определяется по наилучшим условиям приема для второй гармоники частоты

зондирующего сигнала.

От рабочей частоты зависит форма и геометрические размеры антенны,

важной характеристикой которых является поляризация. Передающие антенны

имеют как правило, линейную, а принимающие — круговую поляризацию.

Точность определения местонахождения радиоэлектронного устройства

составляет несколько сантиметров.

Режим работы нелинейного локатора бывает беспрерывным и импульсным.

Мощность локаторов в беспрерывном режиме составляет от 10 до 850 мВт и

ограничена 3-5 Вт, а в импульсном режиме — от 5 до 400 Вт с ограничением в

400 Вт. Причина ограничений кроется в том, что локаторы могут создавать

проблемы в плане электромагнитной совместимости со средствами связи,

навигации, телевидения, датчиками пожарной и охранной сигнализации. Кроме

того, зондирующие излучения имеет отрицательное влияние на операторов,

которые эксплуатируют аппаратуру.

Некоторые современные нелинейные локаторы имеют возможность изменять

мощность зондирующего сигнала. Например, локатор NJE-400 изменяет

мощность от 0,01 до 1 Вт.

Чувствительность приемников современных нелинейных локаторов на-

ходится в пределах 10

-15

- 10

-11

Вт. В импульсных она несколько хуже.

Большинство приемников имеют чувствительность, которая регулируется в

пределах 30-50 дБ. [12]

Дальность действия большинства локаторов не превышает 0,5 м. Глубина

выявления объектов в маскирующей среде зависит от материала, из которого

изготовленные стены, и составляет от нескольких сантиметров до 0,5 м.

Количество одновременно анализируемых гармоник является важной ха-

рактеристикой, которая характеризует преимущества локаторов, выявляющих

больше одной гармоники.

Современные нелинейные локаторы имеют небольшие размеры, вес и

позволяют работать как от электросети, так и от автономных источников пи-

тания. Следует отметить, что нелинейные локаторы полностью не решают задачу

выявления закладок в помещении.

191

Глава 5

Основы криптографии и

шифрования

5.1. Основные принципы криптографии

Одним из первых в истории документально засвидетельствованных примеров

шифрования является шифр Цезаря (I в. до н.э.), который образовывался заменой

одних букв другими соответствующими буквами по всему тексту. Закон замены

был очень простым. Во время шифрования сообщения вместо пятой буквы

латинского алфавита подставлялась вторая, вместо четвертой — первая, вместо

третьей — двадцать шестая и т.д. Во время дешифрования сдвиг необходимо

было выполнить в прямом направлении: вместо первой буквы брать четвертую и

т.д. [16]

В современной терминологии шифр Цезаря и его модификации относятся к

одноалфавитным подстановкам или одноалфавитным заменам.

Предвестником возникновения криптографии стало появление криптоанализа,

который довольно быстро обнаружил слабые места в вышеупомянутых методах

шифрования.

Значительной модификацией одноалфавитной замены является шифр,

который называют квадратом Полибия или тюремной азбукой. В нем символы

алфавита размещают в матрице 5x6, и вместо буквы в письме записывают пару

чисел: номер строки и номер столбца ячейки.

В XVI столетии Д. Кардано изобрел новый тип шифра, основанный на очень

простой, но надежной перестановке букв сообщения. Для шифрования Кардано

предложил использовать квадрат с прорезанными в нем несколькими ячейками.

Ячейки прорезались таким образом, чтобы при повороте квадрата вокруг своего

центра на 90° (а потом — на 180° и 270°) в отверстиях поочередно появлялись

все позиции исходного квадрата по одному разу. При шифровании квадрат

кладут на лист для послания сначала в исходном положении и пишут слева

направо сверху вниз первую порцию сообщения. Для дешифрования необходимо

иметь точную копию того квадрата, которым пользовался шифровальщик, и

повторить с ней те же повороты.

Это устройство достаточно удобно для хранения и обеспечивает хорошую

стойкость шифра. Такие шифры, которые не модифицируют буквы сообщения, а

только изменяют их размещение, называют перестановочными.

После Д. Кардано французским дипломатом Виженером была предложена

модификация шифра замен, получившая название таблицы Виженера. Для

Шифрования по этой схеме требуется таблица из 26 латинских алфавитов, в

каждом из которых по какому-либо закону изменен порядок букв, и секретное

192

слово-пароль, известное только отправителю и получателю сообщения. Такой

шифр получил название многоалфавитной замены.

Следующей модификацией этого способа стало шифрование по книге, когда

отправитель и получатель сообщения договариваются об одинаковой книге

одного и того же издательства. При шифровании отправитель выбирает в ней

произвольное место и записывает вместо пароля, который повторяется под

исходным сообщением на всю его длину, текст из книги, начиная с того места.

Само кодирование выполняется по той же схеме, что и в методе Виженера.

Получатель по другому каналу связи получает страницу и слово в книге, с

которого началось шифрование.

С XIX века криптография перешла на качественно другой уровень: началась

эра цифровой криптографии.

В 20-х годах XX века Г. Вернам предложил автоматизировать шифрование

телетайпных сообщений по следующей схеме. Информация на телетайпной

ленте представляет собой последовательность отверстий и не пробитых

участков, соответствующих "0" и "1". Вернам предложил на передающей

стороне разместить замкнутую в кольцо ленту с достаточно длинной после-

довательностью похожих "0" и "1", выполняющую роль пароля. В момент

передачи очередного импульса в канал связи лента-пароль сдвигается на одну

позицию и с нее считывается текущее двоичное значение. Если был считан "0",

то исходный двоичный сигнал не изменялся, если же на ленте-пароле в этом

месте оказывалась "1", то исходный сигнал инвертировался. На принимающей

стороне должна присутствовать точно такая же лента, и притом — в том же

начальном положении, что и у отправителя.

Таким образом, тут впервые была применена операция сложения по модулю

2, которая стала базовой в цифровой криптографии. Такая операция также

называется "исключающее ИЛИ" и записывается как

⊕

ли XOR (от английского

"Exclusive OR"). В отношении сложения по модулю 2 интересен еще один факт:

существование обратной операции, то есть, вычитания по модулю 2, которая

часто применяется в разнообразных современных шифрах и схемах.

Другим интересным моментом оказалось то, что, выполнив ленту длиной,

равной длине сообщения, можно сделать шифр абсолютно стойким.

Недостатком такой схемы является неудобство хранения большого пароля и

его одноразовость.

5.2. Классификация шифров

Первым принципиальным признаком, позволяющим провести разделение

шифров, является объем информации, который неизвестен третьей стороне. Если

злоумышленнику совершенно неизвестен алгоритм выполненного над

сообщением преобразования, то шифр называют тайнописью. То есть, тай-

нопись является обычным кодированием информации или представлением ее в

другом виде. При этом третьей стороне неизвестен сам принцип кодирования.

[16]

193

В свое время А. Кергофф выдвинул идею о том, что раскрытие самого

алгоритма не должно ни на шаг приближать к закрытому сообщению. Это

должно достигаться базированием всего алгоритма шифрования на небольшом

объеме тайной информации. Эта идея легла в основу всей современной

криптографии и получила название принцип Кергоффа.

В противоположность тайнописи, криптографией с ключом называют сегодня

алгоритмы шифрования, в которых сам алгоритм преобразований широко

известен и доступен каждому, однако шифрование выполняется на основе

небольшого объема информации — ключа, известного только отправителю и

получателю сообщения. В современной криптографии размер ключа составляет

от 56 до 4096 бит.

Все криптоалгоритмы с ключом делятся на симметричные и асимметричные.

В симметричных криптоалгоритмах ключи, используемые на передающей и

принимающей стороне, полностью идентичны. Такой ключ несет в себе всю

информацию о процессе утаивания сообщения и потому не должен быть

известен никому, кроме участников переговоров. По этой причине тут часто

применяют термин тайный ключ, а сами системы называют шифрами на тайном

ключе. [16]

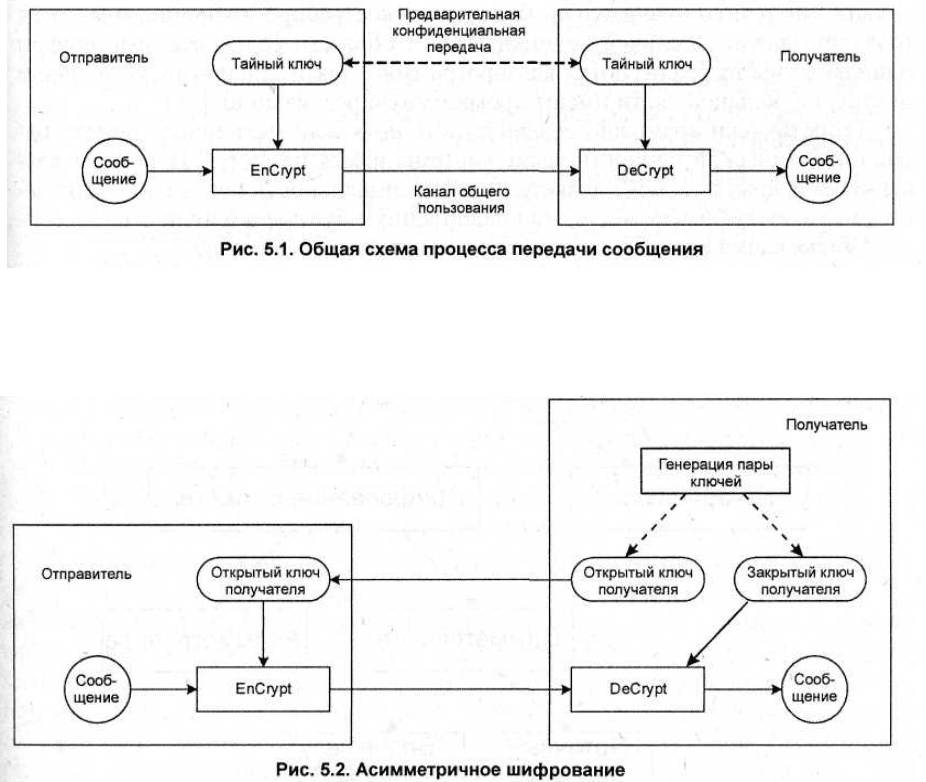
Общая схема процесса передачи сообщения представлена на рис. 5.1.

В асимметричном шифровании (рис. 5.2) для шифрования сообщения ис-

пользуется один ключ, а для дешифрования — другой.

194

Таким образом, прочитать зашифрованный текст можно только при наличии

ключа дешифрования. Поэтому ключ шифрования может быть известен всем

пользователям сети и называться открытым ключом, а ключ дешифрования

называют закрытым. Сами же асимметричные системы получили название

шифра на открытом ключе. Асимметричные шифры нет смысла использовать

для защищенного хранения документов. Их назначение — защита сообщений,

электронной почты и т.д.

Следующим критерием классификации шифров является схема обработки

ими потока информации. Согласно ему, симметричные криптоалгоритмы

делятся на поточные и блочные шифры. Поточный шифр способен обрабатывать

информацию побитно. Такая схема очень удобна в каналах последовательной

связи, где сам процесс передачи информации может обрываться в любой момент,

а потом продолжаться дальше.

Такая обработка информации является довольно медленной и потому,

учитывая возможности современных процессоров выполнять параллельную

обработку, применяют другие принципы криптографических преобразований,

носящих название блочных шифров. Основным законом блочного шифрования

является "или блок или ничего", то есть, преобразования могут осуществляться

только над информацией строго определенного объема. Размер блока на

сегодняшний день составляет 64, 128 или 256 бит. Частичное шифрование

(например, попытка обработать 177 бит) невозможно. Блочное шифрование

получило значительно более широкое распространение, благодаря развитию

вычислительной техники. Таким образом, если поточные шифры одинаково

часто реализуются как программно, так и аппаратно, то блочные шифры по

большей части имеют программную реализацию. [16]

Теоретически возможно создание поточных асимметричных систем, однако

практической ценности такие системы иметь не будут. Целью шифрования на

открытом ключе является конфиденциальность некоторого сообщения, поэтому

тут имеет место этап накопления в буфере и блочность.

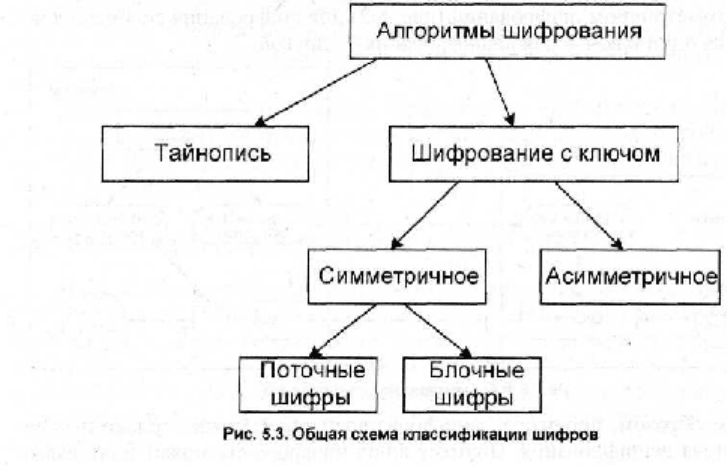
Общая схема классификации шифров представлена на рис. 5.3.

195

Как было отмечено выше, абсолютная стойкость шифра может быть дос-

тигнута только в случае, когда размер ключа равен или превышает размер

исходного сообщения. Если же размер ключа меньше объема исходного со-

общения, тогда теряется непредвиденность. Причина этого кроется в

избыточности любого национального языка. Любой человек может определить

из какого угодно небольшого текста, возможен (имеет смысл) он или нет в

родном языке. Ключ считается подобранным, если в результате дешифрования в

сообщении определилась часть, имеющая смысл. Таким образом, любой шифр,

длина которого меньше длины передаваемого сообщения, не является абсолютно

стойким. Его можно всегда раскрыть хотя бы полным перебором всех

возможных ключей до появления фразы, имеющей смысл. То есть, можно

говорить только о практической стойкости шифра.

Практически стойким называют шифр, к которому нельзя применить какие-

нибудь результативные методы атаки, кроме полного перебора всех возможных

ключей.

Рассмотрим основные виды атак, которым должен противостоять стойкий

шифр.

■ Атака на основе шифротекста — это попытка злоумышленника вы

явить или исходный текст, или ключ шифрования с помощью достаточно

большого объема зашифрованных данных.

■ Атака на основе известного открытого текста — ситуация, когда

злоумышленник знает и исходный, и преобразованный в процессе

шифрования текст и желает узнать о ключе шифрования. Дело в том,

что злоумышленник в 99% случаев знает какую-нибудь дополнительную

информацию об исходном тексте, поэтому стойкость шифров такой атаке

(то есть, невоспроизводимость относительно ключа) является такой же

важной целью их разработки как и защита от первого типа атак.

■ Атака на основе выбранного открытого текста является модифика-

цией предыдущей атаки в том случае, когда злоумышленник находится

среди обслуживающего персонала системы и может навязать службе

шифрования, какую информацию необходимо передать по крипто-

каналу. Практически стойкий шифр должен выдерживать огромное

количество подобных попыток, не давая злоумышленнику никакой

новой информации о ключе шифрования.

Если на протяжении достаточно большого промежутка времени (десятки лет)

на какой-то шифр не найдено ни одного способа взлома, то он считается

надежным шифром. Однако следует помнить, что в любой момент какой-то

шифр может покинуть совокупность надежных шифров в связи с открытием

какой-нибудь новой математической теоремы или метода криптоанализа.

Например, после доказательства Дж. Месси и Э. Берлекампом теоремы о том,

что при перехвате 2xN бит шифрующей последовательности линейного регистра

сдвига всегда можно восстановить его внутреннюю структуру, линейные

регистры сдвига покинули класс надежных шифров и применяются только как

составные элементы более сложных криптоалгоритмов. До сих пор не

196

существует теории, позволяющей генерировать надежные на 100% практически

стойкие шифры. [16]

Итак, какой угодно шифр можно открыть простым перебором ключей. Все

зависит от размера ключа, определяющего количество времени на перебор всех

вариантов. Так, если длина ключа составляет 32 бита (4 млрд. вариантов), то

требуется несколько дней (или недель) для его открытия. Ключи длиной 128 бит

в современных надежных шифрах невозможно открыть полным перебором на

современных ЭВМ. Рекомендованная длина ключей для коммерческих целей —

192 бита, а для государственных — 256 бит. То есть, сделан запас на несколько

десятков лет, с учетом бурного развития современных ЭВМ.

5.3. Симметричная криптография

5.3.1. Поточные шифры

Симметричные алгоритмы начали развиваться значительно раньше

асимметричных, потому на данный момент накопилось значительное количество

исследований в этом направлении [16].

Характерной особенностью поточных шифров является побитовая обработка

информации, поэтому шифрование и дешифрование в таких схемах может

прерываться в произвольный момент времени, а также возобновляться в случае

продолжения передачи. Такая обработка информации может быть представлена

в виде автомата, который на каждом своем такте:

■ генерирует по некоторому закону один бит шифрующей последова-

тельности;

■ каким-либо обратным преобразованием накладывает на один бит от

крытого потока этот шифрующий бит и получает зашифрованный бит.

Поясним, почему шифрующую последовательность достаточно ограничить

только одним битом на бит исходного текста. Дело в том, что в арифметике по

модулю 2, к которой относятся любые преобразования над битами, существует

только две обратимые операции: исключающее ИЛИ (оно же сложение по

модулю 2) и отрицание. Обратимой называют функцию, у которой, зная

результат и все операнды, кроме одного, можно восстановить этот неизвестный

операнд.

Таким образом, как бы много ни было создано шифрующих битов на один бит

исходного текста, все они будут накладываться на данный бит путем

комбинации из операций XOR и "Отрицание". Однако отрицание можно вносить

внутрь операции XOR, то есть, для любых а и b:

NOT (a XOR b) = a XOR (NOT b) = (NOT a) XOR b.

Итак, какой бы ни была сложной композиция из шифрующих битов и ис-

ходного, ее всегда можно разделить, то есть, представить в виде:

p XOR F(g

197

где р — исходный бит (от англ. "plain" — "открытий"), g — шифрующие биты, F

— некоторая функция, содержащая в себе операции исключающее ИЛИ и

отрицание. Логично сразу выполнить эти преобразования над промежуточными

битами g

и получить в результате, что вся формула шифрования будет иметь

универсальный вид:

c = p XOR g

где с — зашифрованный бит (от англ. "ciphered" — "зашифрованный").

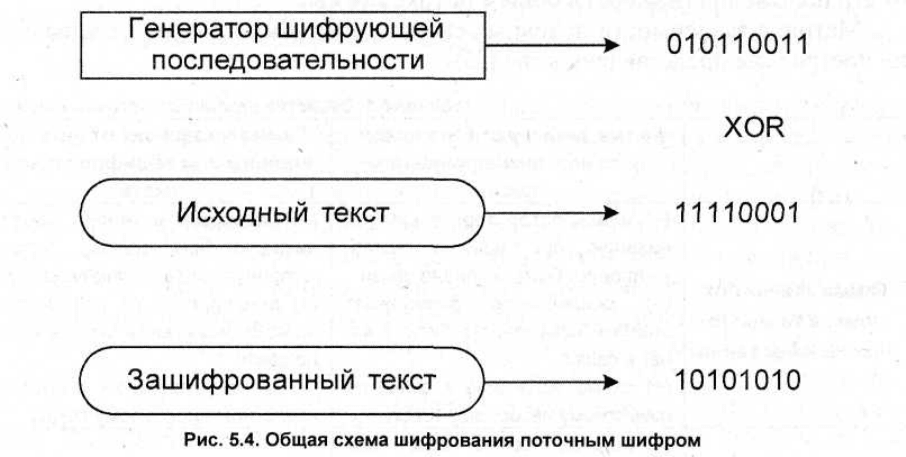
Общая схема шифрования поточным шифром представлена на рис. 5.4 [16].

Все современные поточные шифры работают по данной схеме. Бит шиф-

рования, который появляется на каждом новом шаге автомата, или целый набор

таких битов, принято обозначать символом у (гамма), а сами поточные шифры

получили за это второе название — шифры гаммирования. Эти шифры намного

быстрее своих ближайших конкурентов — блочных шифров — в том случае,

если поточное шифрование реализуется аппаратно. Когда эти алгоритмы

реализованы программно, их скорость мало отличается от блочных, а иногда и

значительно ниже.

Тремя основными компонентами, над которыми вычисляется функция,

порождающая гамму, являются:

■ ключ;

■ номер текущего шага шифрования;

■ ближайшие от текущей позиции биты исходного и/или зашифрованного

текста.

Ключ является необходимой частью гаммирующего шифра. Если ключ и

схема порождения гаммы не являются тайными, то поточный шифр превра-

щается в обычный преобразователь — кодер — скремблер (от англ. "scramble" —

"перемешивать"). Скремблеры широко применяются в системах теле-

коммуникаций для улучшения статистических характеристик передаваемого

сигнала. Частота появления "0" и "1" необходима во многих системах син-

хронизации — по моменту изменения значения (фронта) сигнала с "0" на "1" или

198

с "1" на "0" принимающая сторона корректирует свои генераторы син-

хроимпульсов. Часто в отношении поточных шифров по аналогии с подобными

кодерами применяется термин "скремблер".

Зависимость шифрующего бита от номера текущей позиции, если такая

существует, чаще всего задается номером позиции до ключа очередного бита

гаммы. Просто на каждом такте шифрования над материалом ключа и внут-

ренними переменными поточного шифра выполняются некоторые однотипные

преобразования, и потому каждый шифрующий бит фактически зависит от его

положения (номера) в общем потоке гаммы.

Матрица зависимости основных свойств поточных шифров от идеологии их

построения представлена в табл. 5.1.

Таблица 5.1. Свойства различных поточных шифров

Гамма зависит от бита исход-

ного или зашифрованного

текста

Гамма не зависит от бита ис-

ходного или зашифрованного

текста

Гамма зависит от

номера текущего такта

шифрования

(-) дешифратор теряет синхро-

низацию при ошибке "встав-

ка/пропуск бита" в канале связи.

(-) дешифратор размножает

ошибки "искаженного бита" в канале

связи

(+) схема устойчива к атаке по

известному исходному тексту

(-) дешифратор теряет синхро-

низацию при ошибке "встав-

ка/пропуск бита" в канале связи

(+) дешифратор не размножает

ошибки "искажения бита" в канале

связи

(+) схема устойчива к атакам по

известному исходному тексту

Гамма не зависит от

номера текущего

такта шифрования

(+) дешифратор не теряет син-

хронизацию при ошибке "встав-

ка/пропуск бита" в канале связи

(-) дешифратор размножает

ошибки "искажение бита" в канале

связи

(-) схема неустойчива к атаке по

известному исходному тексту

Таким образом, шифры, которые зависят только от ключа и номера такта

шифрования (правый столбец, верхняя строка в табл. 5.1.) получили наибольшее

распространение в современной практике.

Атаки на шифры гаммирования, не связанные с конкретной их реализацией,

основаны по большей части или на факте значительного отклонения

статистических характеристик гаммы от действительно случайного потока, или

на повторном использовании некоторых частей гаммы в процессе шифрования.

В первом случае отклонение характеристик гаммы не может полноценно

скрыть частотные характеристики исходного текста, и появляется возможность

проведения разнообразных форм частотного и корреляционного криптоанализа.

Во втором случае повторное наложение на исключающее ИЛИ той же

шифрующей последовательности g на новый исходный блок Pj позволяет

злоумышленнику на основе нехитрой формулы:

(Р

XOR g) XOR (Р

XOR g) = Р

XOR Р

199

полностью избавиться от гаммирующей последовательности. А это уже дает

возможность при удачном стечении обстоятельств с помощью специальных

методов, включая подбор букв и статистические исследования, получить из (Р

XOR Р

) отдельно Р

и отдельно Р

Эти методы криптоанализа позволяют сформировать два основных принципа

шифров гаммирования, не зависящие от их конкретной структуры:

■ гамма, порождаемая шифром, должна иметь очень хорошие стохасти-

ческие характеристики;

■ период гаммы шифра должен превышать длину наибольшего из сооб-

щений, которые планируется пересылать с помощью одного и того же

ключа.

Кроме того, следует помнить, что в каналах с возможностями модификации

данных шифры гаммировання полностью беззащитны перед фальсификацией. В

том случае, когда злоумышленник знает побитное размещение данных в

передаваемой последовательности, инвертирование любого бита не может быть

распознано на принимающей стороне. Это приведет к инвертированию

соответствующего бита в декодированном тексте сообщения. Во время

использования поточных шифров в каналах такого рода необходима тщательная

реализация системы подтверждения целостности сообщения.

Наиболее простыми схемами, которые используются в качестве базовых при

построении других, более устойчивых поточных шифров, являются линейные

регистры сдвига - ЛРС (англ. Linear Feedback Shift Registers — LFSR). Их

строение очень простое: устройство представляет собой несколько (20-100) ячеек

памяти, в каждой из которых может храниться один бит информации.

Совокупность бит, которая находится в данный момент в ЛРС, называют его

состоянием. Для выработки очередного бита шифрующей последовательности

(то есть, гаммы), ЛРС выполняет один цикл преобразований, носящий название

такта, по следующему алгоритму:

1. Первый (скажем, крайний справа) бит из последовательности поступает

на вход ЛРС — это очередной бит гаммы.

2. Содержимое всех промежуточных ячеек памяти сдвигается на одну пози-

цию вправо.

3. В пустую ячейку памяти, которая появилась в результате сдвига с левого

края ЛРС, размещают бит, рассчитываемый как операция XOR над значениями

из ячеек ЛРС с заданными номерами.

Естественно, направление сдвига не играет никакой роли, и можно было бы

сформулировать весь этот алгоритм сдвигами "справа налево". Схематически

линейный регистр сдвига изображен на рис. 5.5.

Количество бит, охваченных в ЛРС обратной связью, называют его раз-

рядностью. В случае использования в качестве простого шифра перед началом

процесса в ячейки памяти ЛРС помещают побитно ключ. Как следствие, бит

гаммы, порождаемый на каждом такте, зависит от ключа и от номера данного

такта в общей процедуре шифрования.