Колесников А.А. Синергетические методы управления сложными системами: теория системного синтеза
Подождите немного. Документ загружается.

u
1
u
2
u
1
(x
1
,...,x
4
) u
2
(x
1
,...,x
4
)
x
3
x
4
x
2
3
+ x
2
4
< 1
x
2
3
+ x
2
4
< 1
ψ
1
= x
1
+ β
12
x
2
+ β
13
x
3
ω
−1
;
ψ
2
= x
1
+ β
2
2x
2
+ β
2
4x
4
ω
−1
T
1
˙
ψ
1
(t)+ψ
1
=0; T
2
˙
ψ
2
(t)+ψ
2
=0; T
1
> 0; T
2
> 0,
Bu
1
= −
β
22
T
1
−
β
12
T
2
− β
24
β
12
x
1
+
β
22
β
12
T
2
+2B + β
13
β
22
−
β
12
β
22
T
1
x
2
+
+
β
12
β
22
x
3
− β
24
β
12
x
4
×
x
2
x
3
− x
1
x
4
ω
−2
−
−
β
24
β
22
+
β
22
β
13
T
1
x
3
ω
−1
−
β
13
β
22
−
β
12
β
24
T
2
x
4
ω
−1
;
Bu
2
= −
2B + β
24
−
1
T
1
+
1
T
2
x
1
−
β
13
+
β
22
T
2
−
β
12
T
1
x
2
+
β
24
+
β
13
T
1
x
3
ω
−1
+
+
β
13
+
β
24
T
2
x
4
ω
−1
+
β
13
x
3
− β
24
x
4
x
1
x
4
− x
2
x
3
ω
−2
,
B = β
22
− β
12
ω =
1 − x
2
3
− x
2
4
1/2
u
1
u
2
ψ
1
= x
1
+ β
12
x
2
+ β
13
x
3
ω
−1
=0;
ψ
2
= x
1
+ β
22
x
2
+ β
24
x
4
ω
−1
=0.
x
1
x
2
˙x
3ψ12
(t)=−
β
13
B
x
3ψ12
+
1+
β
24
B
x
3ψ12
;
˙x
4ψ12
(t)=−
1+
β
13
β
22
B
x
3ψ12
+
β
24
β
12
B
x
4ψ12
,
ψ
12
=0
β
22
> 0; β
24
> 0; β
12
< 0; β
13
> 0.
x
1
x
2
x
2
3
+x
2
4
< 1
x
3
x
4
β
1i
β
2i
ψ
1−2
=0
β
22
=1 β
24
=1 β
12
= −1 β
13
=10 B =2 T
1
= T
2
=0, 5
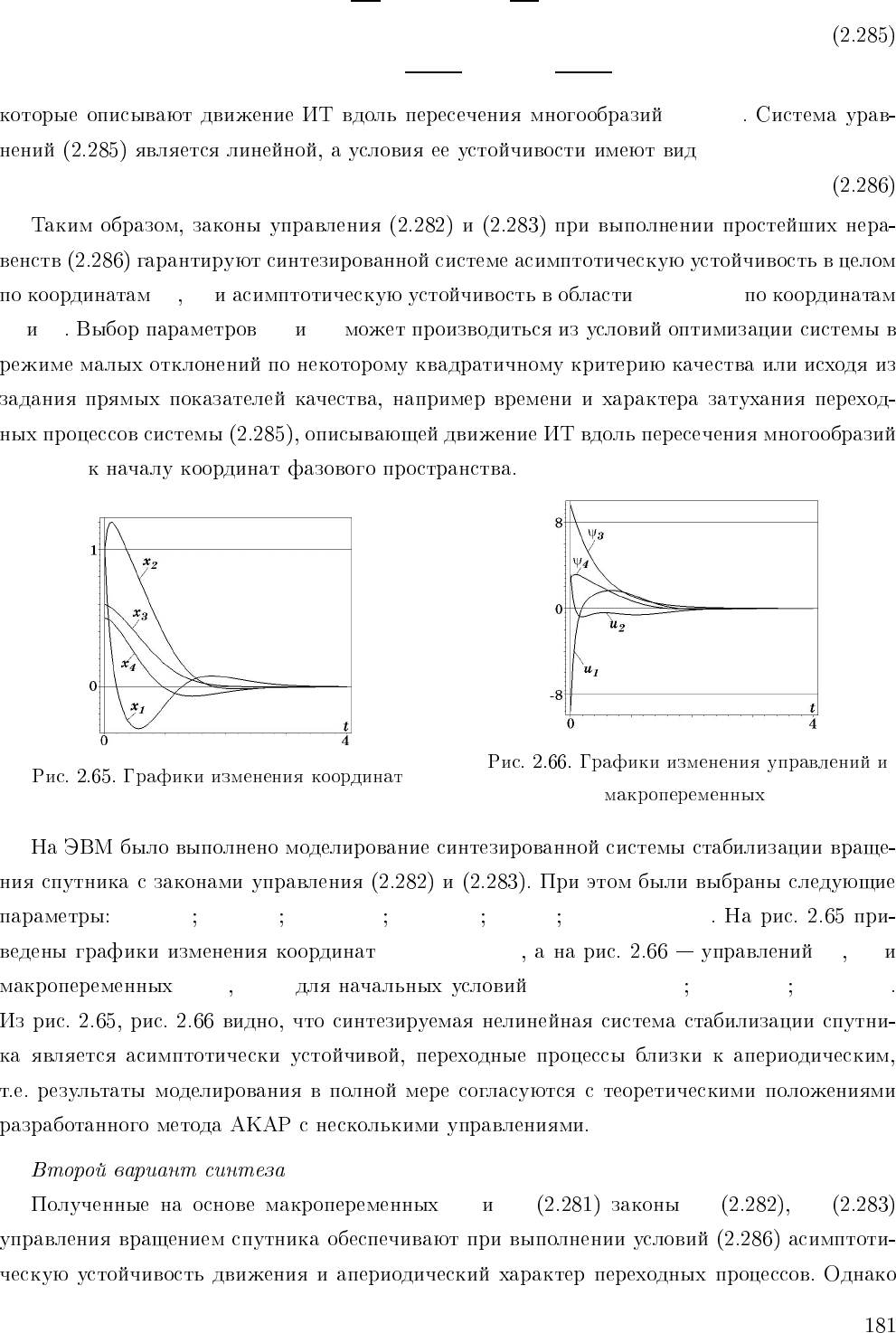
x
1
(t),...,x
4
(t) u
1
u
2
ψ
1
(t) ψ
2
(t) x
10
=˙x
20
=1, 0 x
30
=0, 6 x
40
=0, 5
ψ
1
ψ
2
u
1
u
2

x
2
1
+x
2
3
≈ 1 ω ≈ 0
ψ
3
= γ
1
x
1
+ γ
2
x
2
+ γ
3
x
3
+ x
4
+ γ
4
x
3
3
+ γ
5
x
3
4
;
ψ
4
= ρ
1
x
1
+ ρ
2
x
2
+ ρ
3
x
3
+ x
4
+ ρ
4
x
3
3
+ ρ
5
x
3
4
.
T
3
˙
ψ
3
(t)+ψ
3
=0; T
4
˙
ψ
4
(t)+ψ
4
=0; T
3
> 0; T
4
> 0,
u
3
=2x
1
−
1
γ
1
1+3γ
5
x
2
4
(x
1
ω − x
3
) −
ρ
2
B
1
γ
1
T
3
ψ
3
+
γ
2
B
1
γ
1
T
4
ψ
4
;
u
4
= −2x
1
−
γ
3
− ρ
3
+3(γ
4
− ρ
4
)x
2
3
(x
2
ω − x
3
)+
1
T
3
ψ
3
−
1
T
4
ψ
4
.
u
3
u
4
u
1
u
2
ψ
3
=0 ψ
4
=0 ψ
34
=0
˙x
3ψ34
(t)=−
β
1
x
3ψ34
+ β
2
x
3
3ψ34
ω + x
4ψ34
;
˙x
4ψ34
(t)=−
α
1
x
4ψ34
+ α
2
x
3
4ψ34
ω − x
3ψ34
.
x
3ψ34
= x
4ψ34
=0
x
2
3
+ x
2
4
1
V
ψ34
=0, 5x
2
3ψ34
+0, 5x
2
4ψ34
.
˙
V(t)=−
β
1
x
2
3ψ34
+ β
2
x
4
3ψ34
ω −
α
1
x
2
4ψ34
+ α
2
x
4
4ψ34
ω<0
β
1
> 0; β
2
> 0; α
1
> 0; α
2
> 0,
ψ
34
=0 u
3
u
4
α
1
=
1
γ
1
; α
2
=
γ
5
γ
1
; β
1
=
ρ
3
ρ
2
; β
2
=
ρ
4
ρ
2
,
γ
1
= ρ
1
γ
5
= ρ
5
γ
3
ρ
2
= ρ
3
γ
2
γ
4
ρ
2
= ρ
4
γ
2
γ
2
= ρ
2
ψ
3
ψ
4
x
3
3
x
3
4
ψ
34
=0

(γ
4
= γ
5
= ρ
4
= ρ
5
=0)
ψ
34
=0
α
1
= β
1
= α
α
2
= β
2
=0 x
3ψ
x
4ψ
˙x
3ψ
(t)x
3ψ
+˙x
4ψ
(t)x
4ψ
= −α
x
2
3ψ
+ x
2
4ψ
1 − x
2
3ψ
− x
2
4ψ
1/2
.
x
3
(t)=r(t)sinϕ(t) x
4
(t)=r(t)cosϕ(t)
r
2
= x
2
3ψ
+ x
2
4ψ
˙r(t)=−αr
√
1 − r
2
;
˙ϕ(t)=1.
ψ
34
=0
r(t)=±
1
√
1+ce
αt
; ϕ(t)=ϕ
0
+ t.
α>0 t →∞ r(t)
ψ
34
=0 α<0
r
s
=1 ω
0
=1
ψ
34
=0 T
1
> 0 T
2
> 0 α>0
x
1
x
2
x
3
x
4
x
4
3
+x
2
4
< 1

∗
˙
y = g(y, v, u);
˙
v = h(y, v, u),
y v u g(·)
h(·) y
v
v
y u
∗

ψ(t)
ψ(t)=ϕ(y, v) −
ˆ
ϕ(t),
ϕ
ˆ
ϕ(t)
ϕ(y, v)
ˆ
ϕ(t)
ϕ(y, v) −
ˆ
ϕ =0
v y ∈R
n
ψ
˙
ψ(t)=L(y)ψ,
m ×m L(y) ψ =0
L(y)
∂ϕ
∂y
g(y, v, u)+
∂ϕ
∂v
h(y, v, u) −
˙
ˆϕ = L(y)ϕ(y, v) −L(y)
ˆ
ϕ.
g(y, v, u) h(y, v, u)
γ(y, u) Γ(y) v
∂ϕ
∂y
g(y, v, u)+
∂ϕ
∂v
h(y, v, u) − L(y)ϕ(y, v)=Γ(y)g(y, v, u)+γ(y, u).
Γ(y)
˙
y −
˙
ˆϕ + γ(y, u)+L(y)
ˆ
ϕ =0
˙
z = L(y)z − L(y)
y
0
Γ(y)dy − γ(y, u),
z =
y
0
Γ(y)dy −
ˆ
ϕ.
ψ = ϕ(y, v) −
y
0
Γ(y)dy + z.
ψ =0
ˆ
v
v
ϕ(y, ˆv)=
y
0
Γ(y)dy − z,
ˆ
v
y ∈R
n

v
ψ
ϕ(y, v)
L(y) Γ(y) γ(y) ϕ(y, v)
L(y)
g h
v
g(y, v, u)=g
0
(y, u)+G
1
(y)v;
h(y, v, u)=h
0
(y, u)+H
1
(y)v.
ϕ(y, v)=Fv,
F
Γ(y) L(y) F γ(y, u)
H
T
1
(y) −G
T
1
(y)
F
−1
Γ(y)
T
=
F
−1
LF
T
.
L(y)=L
H
T
1
(y) −G
T
1
(y)
F
−1
Γ(y)
T
=
F
−1
LF
T
.
L
rang
G
T
1
(y) H
T
1
(y)G
T
1
(y) ...
H
T
1
(y)
m−1
G
T
1
(y)
= m; ∀y ∈R
n
.
F F
I
H
T
1
(y) −G
T
1
(y)Γ
T
(y)=L
T
.
Γ(y)
F = I
γ(y, u)=h
0
(y, u) − Γ(y)g
0
(y, u).
˙
z = Lz − L
y
0
Γ(y)dy − h
0
(y, u)+Γ(y)g
0
(y, u);
ˆ
v =
y
0
Γ(y)dy − z,

Γ(y)
L
˙
x = f(x, u);
y = c(x),
x u y
f(x, u) c(x)
˙
z = R(y, z);
u = u(y, z),
z
y = x
u(x)
v
y
T
v
T
T
= α(x)
α : x → α(x)
x ∈R
n+m
x = α
−1
(y, v),
v
x = α
−1
(y, ˆv),
v

˙x
1
(t)=x
2
;
˙x
2
(t)=sinx
1
+ x
3
;
˙x
3
(t)=u;
y = x
1
.
g
0
=0; G
1
=
10
; h
0
=
sin y
u
; H
1
=
01
00
; m =2.
rang
G
T
1
H
T
1
G
T
1
=rang
10
01
=2=m.
00
10
−
1
0
Γ
T
= L
T
.
L λ
1
= λ
2
= −1 Γ =
21
T
L =
−21
−10
.
x
1
= y x
2
=ˆv
1
x
3
=ˆv
2
˙z
1
(t)=− 2z
1
+ z
2
+3y − sin y;
˙z
2
(t)=− (4 + 12y
2
+cosy)z
1
− 3(1 + y
2
)z
2
+12y +30y
3
+2y cos y+
+6(2y − z
1
)
2
y +3(1+y
2
)siny;
u =(3 + 12y
2
+cosy)z
1
+3(1+y
2
)z
2
− 10y − 30y
3
− 2y cos y−
− 6(2y − z
1
)
2
y − 3(1 + y
2
)siny.
x
1
(0) =
1
x
2
(0) = −1 x
3
(0) = 0, 5 z
1
(0) = z
2
(0) = 0
˙x
1
(t)=x
1
+ x
2
;
˙x
2
(t)=x
2
2
+ u;
y = x
1
.

g(y,v, u)=y + v h(y, v,u)=y
2
+ u
∂ϕ
∂y
(y + v)+
∂ϕ
∂v
(v
2
+ u) − L(y)ϕ =Γ(y)(y + v)+γ(y,u).
ϕ = ϕ
1
(y)v.
∂ϕ
1
∂y
v(y + v)+ϕ
1
(v
2
+ u) − L(y)ϕ
1
v =Γ(y)(y + v)+γ(y,u).
∂ϕ
1
∂y
+ ϕ
1
=0;
∂ϕ
1
∂y
y − L(y)ϕ
1
=Γ(y);
Γ(y)y + γ(y, u)=ϕ
1
u.
ϕ
1
= e
−y
L(y)=−1
Γ(y)=e
−y
(1 − y);
γ(y,u)=−e
−y
(1 − y)y + e
−y
u.
y
0
Γ(y)dy = e
−y
y.
˙z(t)=−4z + e
−y
(9 − y)y + e
y
(y − e
y
z)
2
;
u = −7y +3e
y
z − (y − e
y
z)
2
.
x
1
(0) =
1
x
2
(0) = 2 z(0) = 0
