Колесников А.А. Синергетические методы управления сложными системами: энергетические системы
Подождите немного. Документ загружается.

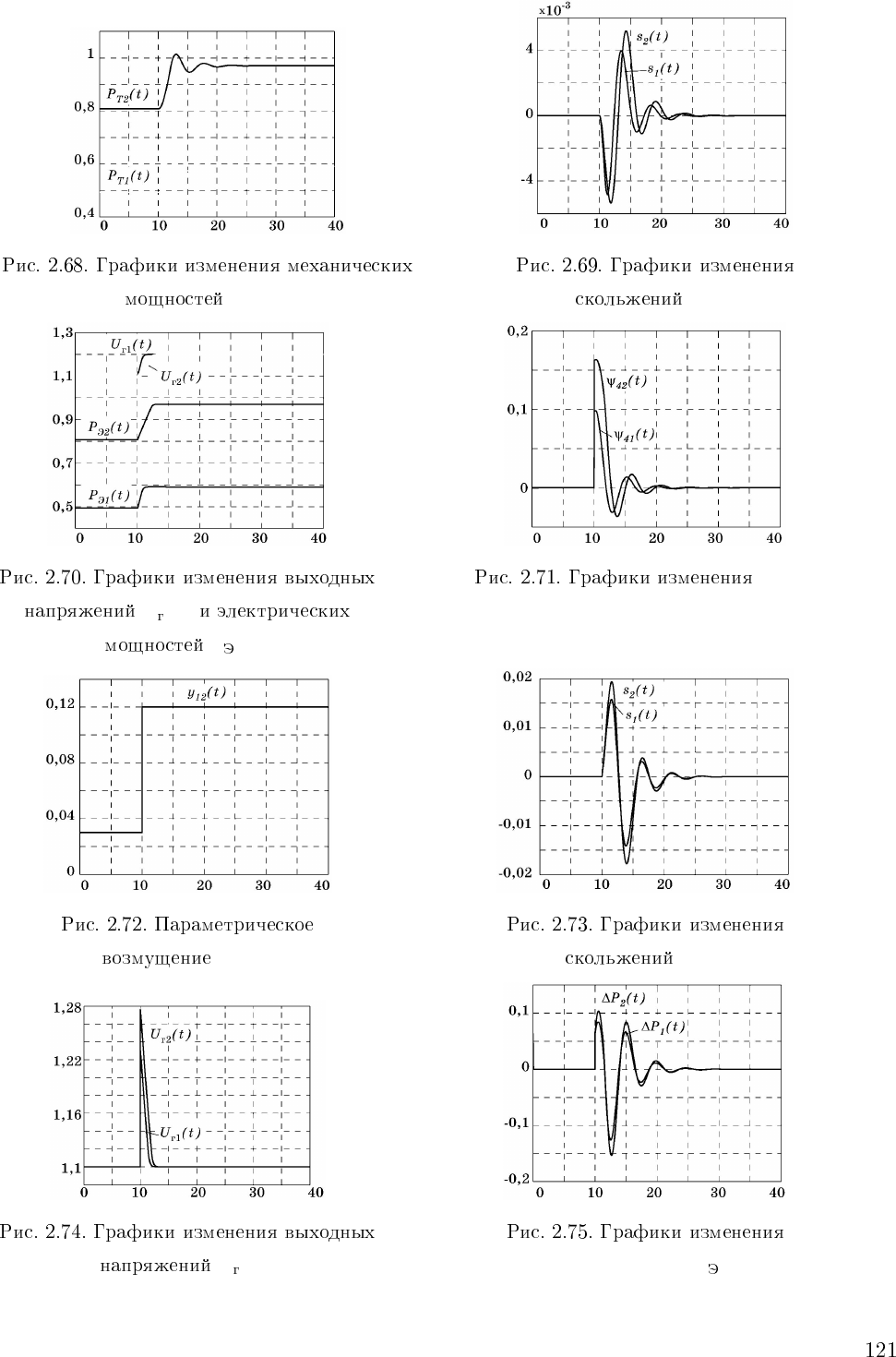
P
Ti
(t) s
i
(t)
U
i
(t)
P
i
(t)
ψ
4i
(t)
y
12
(t) s
i
(t)
U
i
(t) ∆P (t)=P
Ti
(t) − P
i
(t)

x
di
=2, 5 x
di
=0, 28 T
d0i
=6 Tj
i
=9, 17 T
i
=4 T
ci
=0, 4 T
Bi
=0, 25
k
ωi
=20 U
c
=1 C
i
=1, 2 ω
0
=1 y
11
=0, 612 y
22
=0, 487 y
12
=0, 03 α
11
=0, 443
α
22
=0, 426 α
12
=0, 253 U
0i
=1, 1 T
1i
= T
2i
= T
4i
= T
5i
=0, 25
T
3i
=2 β
i
= ξ
i
=1
0, 1 U
1
3 0 U
2
1
t =10
U
0i
=1, 1 U
0i
=1, 2
y
12
y
12
=0,α
12
=0 t
0
<t<t
0
+∆t t
0
=10
∆t =1
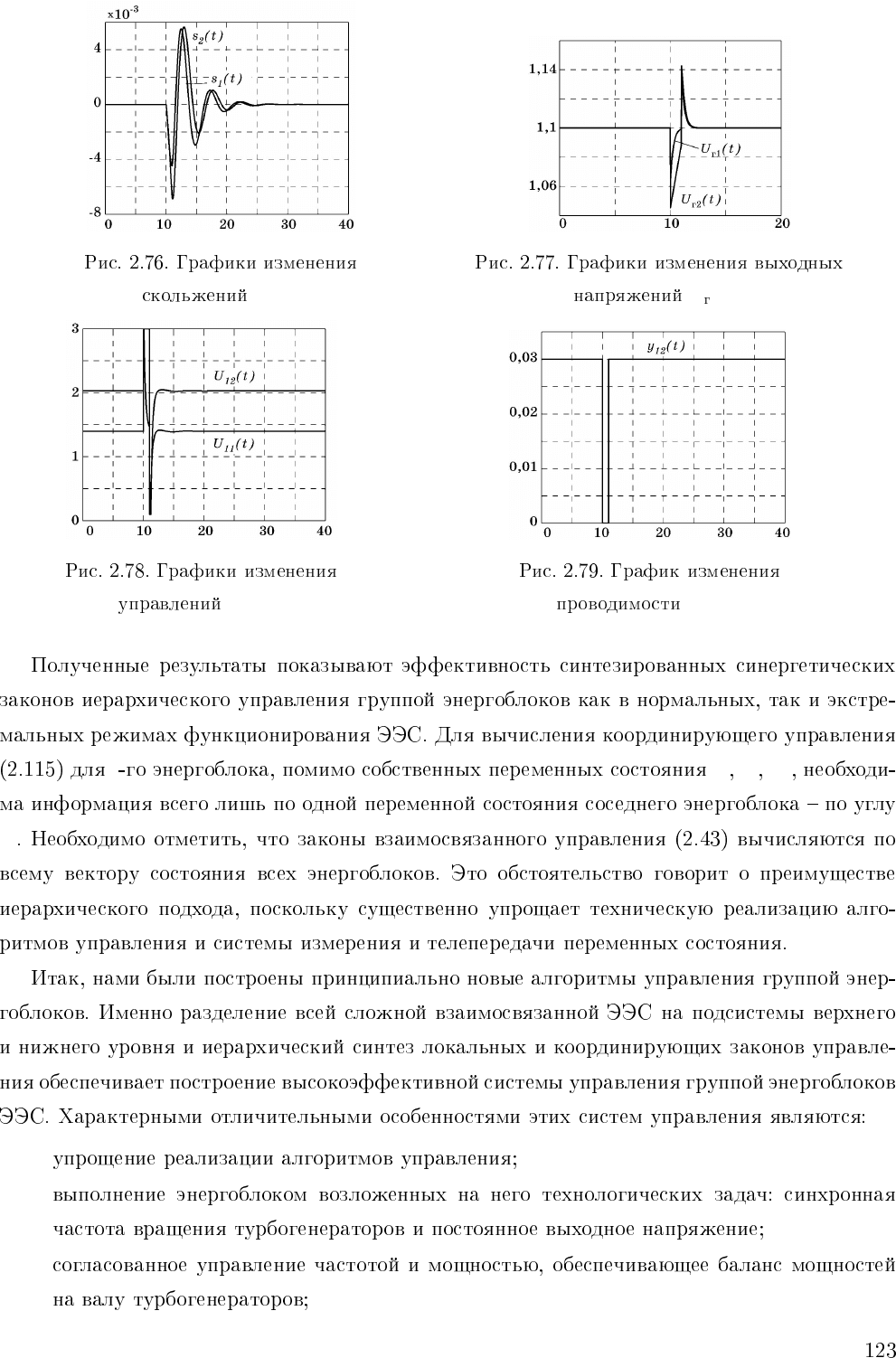
s
i
(t) U
i
(t)
U
1i
(t) y
12
(t)
i δ
i
s
i
w
i
δ
j
•
•
•

•
•
• M
i
(t)=M
0
= const
y
11
y
12
α
11
α
12
w
1
= E
2
q
y
11
sin(α
11
)+E
q
U
c
y
12
sin(δ − α
12
).
w
1
= P
w
1

dδ
dt
= s;
ds
dt
= b
1
(P
T
− w
1
);
dE
q
dt
= b
2
(−E
q
+ b
3
s sin(δ −α
12
)+U
1
);
dP
T
dt
= b
4
(−P
T
+ qC);
dq
dt
= b
6
(−γ(q) − b
5
s + h);
dh
dt
= b
7
(−h + U
2
);
dw
1
dt
=0.
w
1
w
1
w
1
ds
dt
= b
1
(P
T
− w
1
),
dw
1
dt
=0.
ψ
5
= w
1
− ˆw
1
,
ˆw
1
w
1
ˆw
1
= F
1
(s)+z
1
,
F
1
(s) s z
1
d ˆw
1
dt
=
∂F
1
(s)
∂s
ds
dt
+
dz
1
dt
.
˙
ψ
5
(t)+L
1
ψ
5
=0,
L
1
L
1
> 0 L
1
w
1

−
∂F
1
(s)
∂s
b
1
(P
T
− w
1
) −
dz
1
dt
+ L
1
w
1
− F
1
(s) −z
1
.
w
1
∂F
1
(s)
∂s
b
1
w
1
+ L
1
w
1
=0 ⇒
∂F
1
(s)
∂s
= −
L
1
b
1
.
F
1
(s)=−
L
1
b
1
s.
w
1
dz
1
dt
= L
1
P
T
− L
1
−
L
1
b
1
s + z
1
,
ˆw
1
= −
L
1
b
1
s + z
1
.
U
1
U
2
U
2
(s, P
T
,q,h,w
1
)=h +
1
b
7
∂ϕ
1
∂s
ds
dt
+
∂ϕ
1
∂P
T
dP
T
dt
+
∂ϕ
1
∂q
dq
dt
−
1
T
2
b
7
ψ
2
=
= h +
1
b
7
∂ϕ
1
∂s
b
1
(P
T
− w
1
)+
∂ϕ
1
∂P
T
b
4
(−P
T
+ qC)+
+
∂ϕ
1
∂q
b
6
−γ(q) − b
5
s + h
−
1
T
2
b
7
h − ϕ
1
(s, P
T
,q,w
1
)
,
ϕ
1
(s, P
T
,q,w
1
)=γ(q)+b
5
s +
1
b
6
∂ϕ
2
∂s
b
1
(P
T
− w
1
)+
∂ϕ
2
∂P
T
b
4
(−P
T
+ qC)
−
−
1
T
3
b
6
q − ϕ
2
(s, P
T
,w
1
)
,
ϕ
2
(s, P
T
,w
1
)=
P
T
C
−
λ
1
b
4
C
(P
T
− w
1
) −
λ
2
s
b
1
b
4
C
.
w
1
L
1
= b
1
ξ.
x
c
r
c
t =10
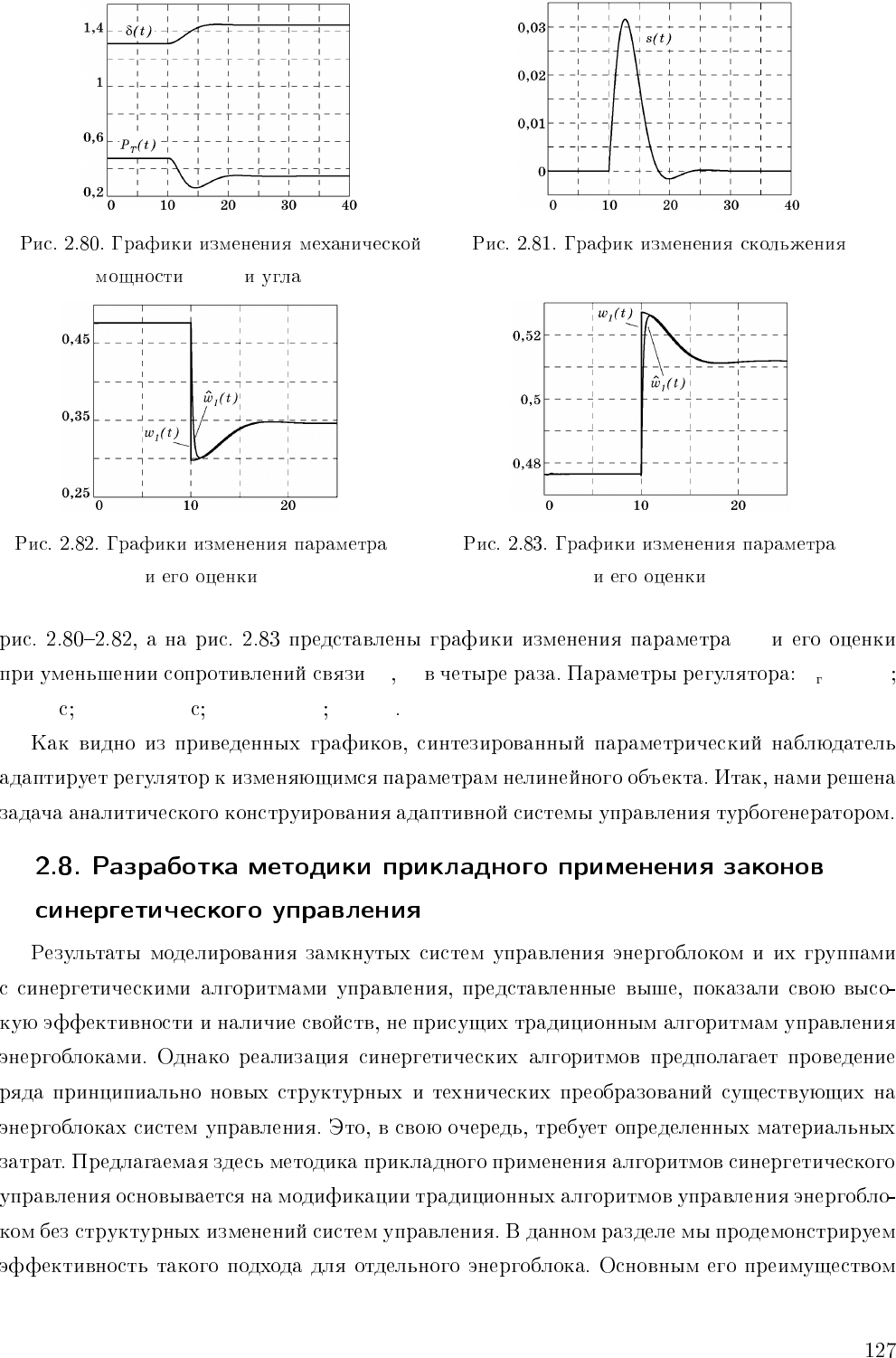
P
T
(t) δ(t) s(t)
w
1
(t) ˆw
1
(t) w
1
(t) ˆw
1
(t)
w
1
x
c
r
c
U
0
=1, 1
T
1
=1 T
2
= T
3
=5 λ
1
= λ
2
=4 ξ =50

µ
PT
= k
u
∆ω +
1
T
u
∆ωdt + k
p
(P
0
T
− P
T
)=k
u
ω
0
s +
ω
0
T
u
sdt+ k
p
(P
0
T
− P
T
),
∆ω = ω
0
− ω = ω
0
s
U = U
f0
+ k
0U
∆U + k
1U
d∆U
dt
+ k
0f
∆ω + k
1f
d∆ω
dt
=
= U
f0
+ k
0U
∆U + k
1U
d∆U
dt
+ k
0f
ω
0
s + k
1f
ω
0
ds
dt
,
U
f0
U
1
= U U
2
= µ
PT
M(t)=M
0
k
0U
=50 k
1U
=7 k
0f
=30 k
1f
=8 k
u
=20
T
u
=2, 5 k
p
=1 U
f0
=0 P
0
T
=0, 785 U =1, 05
0, 1 U
1
3 0 U
2
1
∆ω =0
∆U =0
k
0U
ε
U
=
∆U
U
100% =
U
− U
U
100%,
U
t = 650 ...700 ε
U
=5, 54%
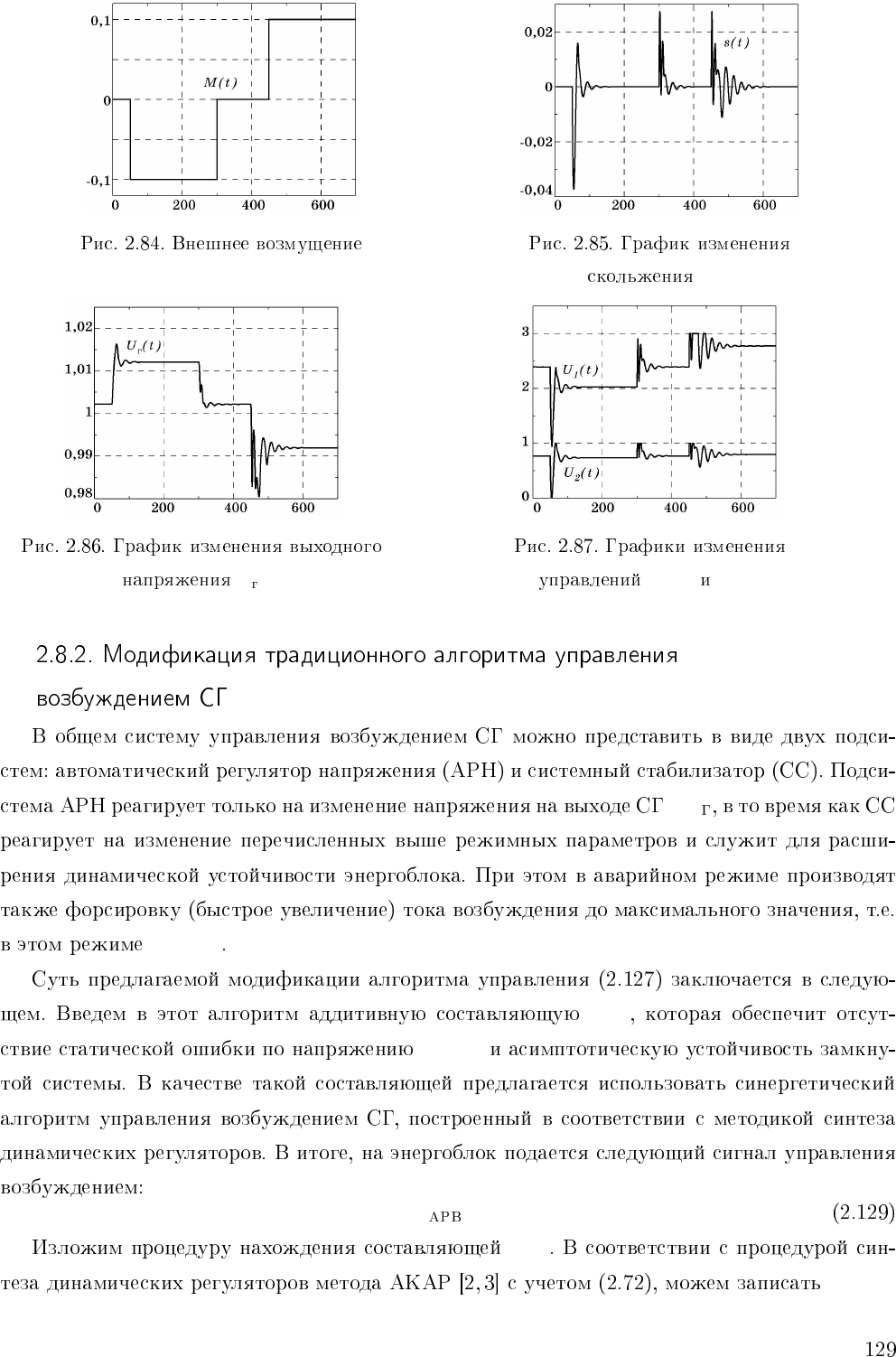
s(t)
U (t) U
1
(t) U
2
(t)
∆U
U
f0
=0
U
syn
ε
U
=0
U
1
= U + U
syn
.
U
syn

dδ
dt
= s;
dE
q
dt
= b
2
(−E
q
+ b
3
s sin(δ − α
12
)+U
syn
+ z);
dz
dt
= η(U
2
− U
2
),
η z
U
2
0
− U
2
=0.
ψ
1
= U
2
0
− U
2
+ λ
1
z,
T
1
˙
ψ
1
(t)+ψ
1
=0.
ψ
1
= U
2
0
−
'
AE
2
q
+2B(δ)E
q
+ D
(
+ λ
1
z,
˙
ψ
1
(t)=
∂ψ
1
∂E
q
dE
q
dt
+
∂ψ
1
∂δ
dδ
dt
+
∂ψ
1
∂z
dz
dt
.
U
syn
U
syn
(δ, s, E
q
,z)=E
q
− b
3
s sin(δ −α
12
) −
∂ψ
1
∂δ
s + λ
1
η(U
2
− U
2
)+
1
T
1
ψ
1
∂ψ
1
∂E
q
b
2
,
∂ψ
1
∂δ
= −2E
q
∂B(δ)
∂δ
=2E
q
U
c
y
12
x
d
(sin(δ − α
12
) − y
11
x
d
sin(δ − α
12
+ α
11
))
∂ψ
1
∂E
q
= −2AE
q
−
2B(δ)
ψ
1
=0
T
1
> 0
U
1
(δ, s, E
q
,z)=U
f0
+ k
0U
∆U + k
1U
d∆U
dt
+ k
0f
ω
0
s + k
1f
ω
ds
dt
+
+ E
q
− b
3
s sin(δ − α
12
) −
∂ψ
1
∂δ
s + λ
1
η(U
2
− U
2
)+
1
T
1
ψ
1
∂ψ
1
∂E
q
b
2
,
