Кочетков П.А. Пособие по математике для поступающих на дистанционное обучение в МГИУ
Подождите немного. Документ загружается.

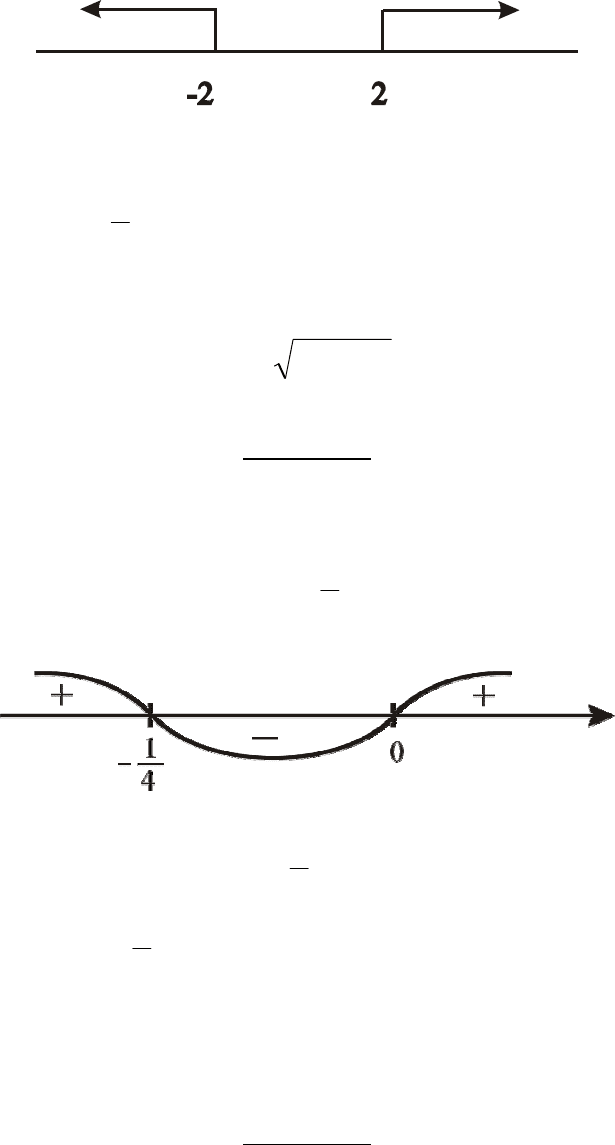
11
2-ой случай: х ≥ 2.
Получаем: х –2 ≥ 2х, х
≤ –2.
Получаем систему:
−≤
≥
2
,2
x
x
Система не имеет решения.
Ответ:
.
3
2
<x
8) Найти область определения функции
xxy +=
2
4
Решение:
Область определения находится из неравенства
,04
2
≥+ xx
тогда
0
4
1
4)14( ≥
+⋅=+⋅ xxxx
Получаем:
.
4
1
,0 −≤≥ xx
Ответ:
.0,
4
1
≥−≤ xx
9) Найти область определения функции:
).2lg(
2
xxy −=
Решение:
Область определения находится из неравенства:
2х – х
2
> 0
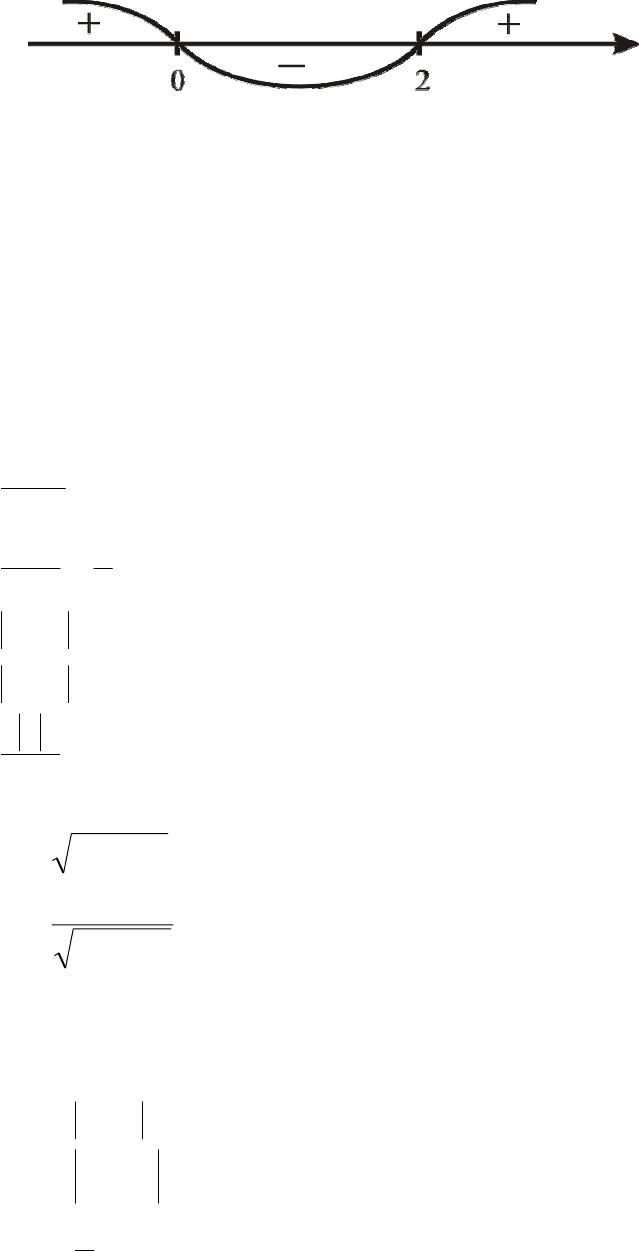
12
Тогда: х (х – 2) < 0.
Получаем: 0 < x < 2.
Ответ: 0 < x < 2.
1.3. Задачи для самостоятельного решения
1)
082
2
≤
−
− xx
(– 2 ≤ х ≤ 4).
2)
02
2
>−− xx
(х < –1, x > 2).
3)
3
2
≤
−x
x
(x < 2, x ≥ 3).
4)
xx
2
1
3
≥
+
(– 1 < x < 0, x ≥ 2).
5)
32 =−x
(x
1
= –1, x
2
= 5).
6)
2
2 xx =−
(x
1
= –2, x
2
= 1).
7)
2
1
≥
−x
x
(1 < х ≤ 2).
Найти область определения функций:
8)
2
9 xxy −=
9)
2
6
1
xx
y
+
=
10)
)10lg(
2
xxy +=
Построить графики:
11)
2
+
= xy
12)
4
2
−= xy
13)
x
y
1
=
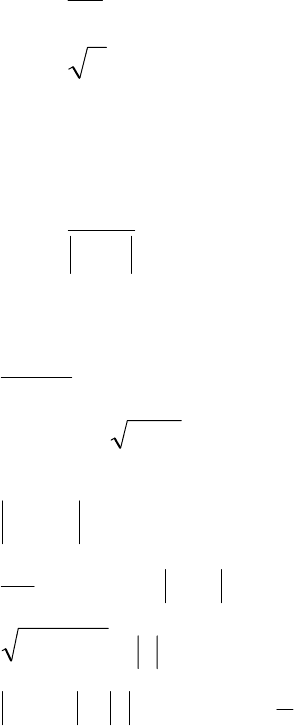
13
14)
2
1
x
y =
15)
xy =
16)
8
xy =
17)
11
xy =
18)
1
1
+
=
x
y
1.4. Задачи повышенной сложности
1) 31
1
2
2
2
=++
+
x
x
(x
1
= 0; x
2
= 1; x
3
= -1).
2)
01)4(
2
=−⋅− xx (x
1
= 1; x
2
= 2).
3) x
2
+ y
2
= 2x – 4y –5 (x = 1; y = -2).
4)
24
2
+≥− xx ((x ≤ 1; x ≥ 3).
5)
12
1
2
2
−−≤+ xx
x
(x = 1).
6)
24
2
+≥− xxx
(x = 2).
7)
542 =
+
− xx (x = -
3
1
; x = 3).

14
2. ПОКАЗАТЕЛЬНЫЕ И ЛОГАРИФМИЧЕСКИЕ
УРАВНЕНИЯ И НЕРАВЕНСТВА
2.1. Основные формулы и определения
Показательная функция: y = a
x
, где 0 < a < 1 или a > 1.
Отметим, что a
x
> 0 для любого х.
Свойства показательной функции:
1)
yxyx
aaa
+
=⋅
2)
(
)
kx
k
x
aa
⋅
=
Решение многих показательных уравнений основывается
на утверждении, что если
).()( то,
)()(
xgxfaa
xgxf
==
Если а
х
> a
y
, то при 0 < а < 1 : x < y;
если a > 1, то x > y.
Если а
х
< a
y
, то при 0 < а < 1 : x > y;
если же a > 1, то x < y.
Логарифмическая функция:
,log xy
a
=
где 0 < а < 1 или а > 1.
По определению: х = а
y
.

15
Свойства:
1) )(logloglog yxyx
aaa
⋅
=+ .
2)
=−
y
x
yx
aaa
logloglog
3)
xkx
a
k
a
loglog ⋅=
4)
x
k
x
a
a
k
log
1
)(log ⋅=
5)
a
x
x
b
b
a
log
log
log =
Решение многих логарифмических уравнений основывается
на утверждении, что если:
),(log)(log xgxf
aa
=
то f(x) = g(x).
Если
,)(log bxf
a
= то
b
axf =)( .
Если
yx
aa
loglog > , то при 0 < а < 1 получаем, что х < y;
если a > 1, то x > y.
Если
yx
aa
loglog < , то при 0 < а < 1 получаем, что х > y;
если же a > 1, то x < y.
2.2. Решение стандартных задач
1) Решить уравнение:
22
42
2
−
=
xx
.
Решение:
Согласно свойствам показательной функции:
44)22(222
224
−
−
−
=
=
xxx

16
Тогда:
44
22
2
−
=
xx
.
В результате:
44
2
−
= xx .
Решаем квадратное уравнение:
044
2
=
+
− xx
.2
2
04
2
44144
2,1
=
±
=
⋅−±
=x
Ответ: х = 2
2) Решить уравнение: 4
х
– 2
х
= 2
Решение:
Обозначим:
x
y 2= , тогда
22
24 y
xx
== .
Получаем квадратное уравнение:
02
2
=−− yy .
Решение:
2
31
2
04
2
)2(411
2,1
±
=
±
=
−⋅−±
=x
.
x
y 22
2
31
1
1
==
+
= , тогда х
1
= 1
1
2
31
2
−=
−
=y – нет решения.
Ответ: х
1
= 1.
3) Решить уравнение:
8244
1
=
⋅
−
−
xx
.
Решение:
Обозначим:
x
y 2= , тогда
22
24 y
xx
== ,
2
2
2
1
x
x
=
−
.
Получаем уравнение:
.82
2
4
22
=−=⋅− yy
y
y
Решаем:
2
62
2
)8(442
2,1
±
=
−⋅−±
=y
x
y 24
2
62
1
==
+
= , тогда х
1
= 2.
2
2
62
2
−=
−
=y – нет решения.

17
Ответ: х = 2.
4) Решить уравнение:
72
2
42
−
−
=
x
x
.
Решение:
Преобразуем:
.22
144
2
−
−
=
x
x
Тогда:
1442 −=− xx
1-ый случай: х < 2.
Получаем: – х + 2 = 4х – 14, 5х = 16.
Решаем систему:
<
=
2
,
5
16
1
x
x
– нет решения.
2-ой случай: х
≥
2.
Получаем: х – 2 = 4х – 14, 3х = 12.
Решаем систему:
≥
=
2
,4
2
x
x
– решение: 4
2
=
x .
Ответ: х = 4.
5) Решение уравнение:
xxx
365812163
⋅
=
⋅
+
⋅
.
Решение:
Преобразуем:
xxxx
945)9(2)4(3
22
⋅⋅=⋅+⋅ .
Разделим обе части на
x2
9 :
.
9
4
52
9
4
3
2 xx
⋅=+
⋅
Обозначим:
.
9
4
x
y
=
Тогда получаем квадратное уравнение:
,523
2
yy =+
0253
2
=+− yy .
6
15
32
324255
2,1
±
=
⋅
⋅⋅−±
=y
.

18
x
y
==
+
=
9
4
1
6
15
1
, но
0
9
4
1
=
.
Поскольку:
x
=
9
4
9
4
0
, получаем х
1
= 0
Далее:
.
3
2
6
4
6
15
2
==
−
=y
Поскольку:
x
=
=
9
4
9
4
3
2
2
1
, получаем
2
1
2
=x .
Ответ: х
1
= 0,
2
1
2
=x .
6) Решить неравенство: .93
314
+
+
≥
xx
Решение:
Преобразуем:
(
)
62
3
23
339
+
+
+
==
x
x
x
.
Тогда неравенство примет вид:
6214
33
+
+
≥
xx
Откуда: 6214
+
≥+ xx ,
или
2
5
,52
≥≥ xx .
Ответ:
2
5
≥x
.
7) Решить неравенство: 5
2x+1
> 5
x
+4.
Решение:
Обозначим:
x
y 5= , тогда:
2212
5555 y
xx
⋅=⋅=
+
.
Получаем неравенство:
45
2
+> yy .
()
0
5
4
1545
2
>
+−=−− yyyy .

19
Используем метод интервалов:
Решение: y > 1,
5
4
−<y
0
515 =>
x
, тогда х > 0
5
4
5
−<
x
– нет решения.
Ответ: х > 0.
8) Решить уравнение:
3)13(log)1(log
22
=
+
+
+
xx
Решение:
Преобразуем:
3)13)(1(log
2
=
+
+
xx
В результате получаем систему уравнений и неравенств:
>+
>+
=
+−
⇒
>+
>+
=++
0
3
1
01
0
3
7
)1(3
013
01
2)13)(1(
3
x
x
xx
x
x
xx
В результате:
−>
−>
−==
3
1
1
3
7
,1
x
x
xx
Решение этой системы:
решениянет
3
7
1
2
1
−−=
=
x
x
Ответ: х = 1.

20
9) Решить уравнение:
2lg3lg
2
−=− xx
Решение:
Обозначим:
.lg,lg
22
yxyx ==
Тогда:
023
2
=+− yy .
Решение:
2
13
2
2493
2,1
±
=
⋅−±
=y
11
lg2 xy == , откуда
2
1
10=x .
22
lg1 xy == , откуда
1
2
10=x .
Ответ:
2
1
10=x , 10
2
=
x .
10) Решить уравнение:
.2)83(log
3
x
x
−=−
Решение:
По свойствам логарифмов:
x
xx
3
3
383
2
2
==−
−
.
Преобразуем:
22
3383
=
⋅−
xx
Обозначим:
y
x
=3 , тогда
22
3 y
x
= .
Тогда получаем:
0)9)(1(98
2
=−+=−− yyyy .
Приходим к системе
>
=
−
+
0
0)9)(1(
y
yy
В результате имеем:
x
y 39 == , тогда х = 2.
Ответ: х = 2.
11) Решить неравенство:
6lg5lg
2
−≥ xx .
Решение:
Обозначим:
x
y
l
g
=
, тогда xy
22
lg= .
Тогда:
65
2
−≥ yy .
