Кочергин В.И. Теория многомерных цифро-векторных множеств

Подождите немного. Документ загружается.

Список обозначений и сокращений

µ (i – 1) = 0 ∨ … ∨ (i – 1) – непрерывное множество цифр ОЦК

M(i) = 0 ∨ … ∨ i = 1 ∨ … ∨ i = … = i – любое цифровое множество, содер-

жащее цифру i

(i) – кодовое расстояние между кодовыми комбинациями из i разрядов

операнда A

(i) – весовые значения кодовых комбинаций из i разрядов операнда A

a,x

– кодовые расстояния между кодовыми комбинациями систематиче-

ского кода (A – информационная часть кода, X – контрольная часть кода)

(2,3) – кодовые расстояния контрольной части квазисовершенного двух-

фазного кода

(3,3) – кодовые расстояния контрольной части квазисовершенного трех-

фазного кода

a,x

(m;2,3) – кодовые расстояния системного многофазного кода (m – чис-

ло фаз информационной части кода; 2,3 – контрольная часть квазисовер-

шенного двухфазного кода)

a,x

(m;3,3) – кодовые расстояния системного многофазного кода (m – чис-

ло фаз информационной части кода; 3,3 – контрольная часть квазисовер-

шенного трехфазного кода)

Глава 1

ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ

Предложенный в [17] нестандартный подход к управляющим дискретным

логическим устройствам и цифровой технике включает в их состав не только

машинную арифметику и цифровые системы управления, но и электропривод,

преобразовательную измерительную и силовую технику и т.д. Предлагаемая

вниманию теория многомерных цифро-векторных множеств является инстру-

ментом для синтеза в этих областях техники оптимальных устройств, исходя

из расширенного натурального ряда чисел N

1.1. Обычные двухзначные логические функции

в многомерном цифровом пространстве

Первые понятия, с которых начинается любая теория, должны быть яс-

ны и приведены к самому наименьшему числу. Только тогда они могут слу-

жить прочным и достаточным фундаментом этой теории.

Одним из таких понятий является представление обычной двухзначной

логической функции в многомерном цифровом пространстве. Прежде чем вы-

полнить это представление, дадим некоторые

пояснения.

Во-первых, в работе будут использоваться только позиционные системы

представления числа, история которых начинается за две тысячи лет до н.э.,

когда вавилоняне [18] употребляли шестидесятеричную систему счисления с

позиционным принципом записи числа. Современное представление позици-

онной системы счисления определяется следующим образом: «Систему счис-

ления называют позиционной, если одна и

та же цифра может принимать раз-

личные численные значения в зависимости от номера местоположения (разря-

да) этой цифры в совокупности цифр, представляющих заданное число. Пози-

ционные системы разделяют на однородные и смешанные. Во всех разрядах

числа, представленного в однородной системе, используются цифры из одного

и того же множества. Например, в обычной десятичной системе во всех разря-

дах любого числа используются цифры из множества {0, 1, ... , 9}, в двоичной

Математика – это не царица наук, она

анимает в мире иное, куда более почетное

положение: она является служанкой (естест-

венных и гуманитарных) наук, помогая им,

доставляя им адекватный аппарат для описа-

ния всевозможных фактов и явлений.

И.М. Яглом

Пространство есть не что иное, как ча-

стный случай трижды протяженной величины.

К.Ф. Гаусс

Глава 1

системе – цифры из множества {0, 1} и т.п. В смешанных системах множества

цифр различны для разных разрядов. В тех случаях, когда в позиционной сис-

теме для каждой цифры имеется отдельный символ, её называют системой с

непосредственным представлением чисел. В позиционных системах с кодиро-

ванием чисел количество символов меньше, чем количество цифр, а каждая

цифра кодируется определенной комбинацией из нескольких символов» [21].

Во-вторых, под кодом будем понимать «правило преобразования сообще-

ния из одной символьной формы представления (исходного алфавита) в дру-

гую (объектный алфавит)» [22]. В нашем случае цифры натурального ряда

конкретного основания системы счисления составляют одну символьную сис-

тему (систему с непосредственным представлением чисел). Другая символьная

система определяет принцип кодирования, где обычно количество символов

меньше, чем количество цифр кодируемого основания системы счисления.

В-третьих, поскольку в большей части коды, в том числе и система с непо-

средственным представлением чисел, являются циклическими, то необходимо

дать определение циклического кода: «Подпространство V наборов длины n

называется циклическим подпространством или циклическим кодом, если для

любого вектора V = (a

n–1

, a

n–2

, ..., a

) из подпространства V вектор V' =

= (a

, a

n–1

, a

n–2

, ..., a

), получаемый в результате циклического сдвига компонен-

та вектора V на единицу вправо, также принадлежит подпространству V'» [19].

Теперь можно приступить к представлению обычной двухзначной логиче-

ской функции в многомерном цифровом пространстве.

Обычной двухзначной логической функцией, в дальнейшем логической

функцией (ЛФ

либо, опуская индекс 2, ЛФ) y = f (x

, ... , x

) называется

функция, принимающая, как и её аргументы x

, ... , x

, два значения, кото-

рые обозначим, чтобы отличать от сигналов 0 и 1 обычного цифрового кода

(ОЦК), символами 0* и 1*.

Поскольку число различных наборов значений аргументов ЛФ конечно и

равно 2

, любая ЛФ может быть задана (на примере k = 3) таблицей истинно-

сти (табл. 1.1.1).

Таблица 1.1.1

ОЦК x

0 0* 0* 0* 0*

1 0* 0* 1* 1*

2 0* 1* 0* 1*

3 0* 1* 1* 0*

4 1* 0* 0* 1*

5 1* 0* 1* 0*

6 1* 1* 0* 0*

7 1* 1* 1* 1*

В таблице наборы значений аргументов расположены в порядке возрастания:

сначала идет набор (иное название набора – кодовое слово или кодовая комби-

нация), представляющий собой двоичное расположение числа 0 (0* , ... , 0*),

затем следует набор, являющийся двоичным расположением числа 1; за ним

Основные положения теории

записывается набор, соответствующий числу 2, и т.д. Последний набор со-

стоит из К единиц (1* , ... , 1*) и является двоичным разложением числа на-

турального ряда (2

– 1). Такое кодирование цифр натурального ряда называ-

ется двоичным.

Если всем наборам значений аргументов ЛФ y = f (x

1 , ... ,

) поставить в

соответствие сигналы ОЦК от 0 до (2

– 1), т.е. цифры расширенного нату-

рального ряда, то каждый аргумент x

(i = 1, ..., K) и сама ЛФ будут представ-

лять собой определенные цифровые множества, что для нашего примера будет

выражено следующим образом:

= 1 ∨ 3 ∨ 5 ∨ 7; x

= 2 ∨ 3 ∨ 6 ∨ 7; x

= 4 ∨ 5 ∨ 6 ∨ 7; y = 1 ∨ 2 ∨ 4 ∨ 7.

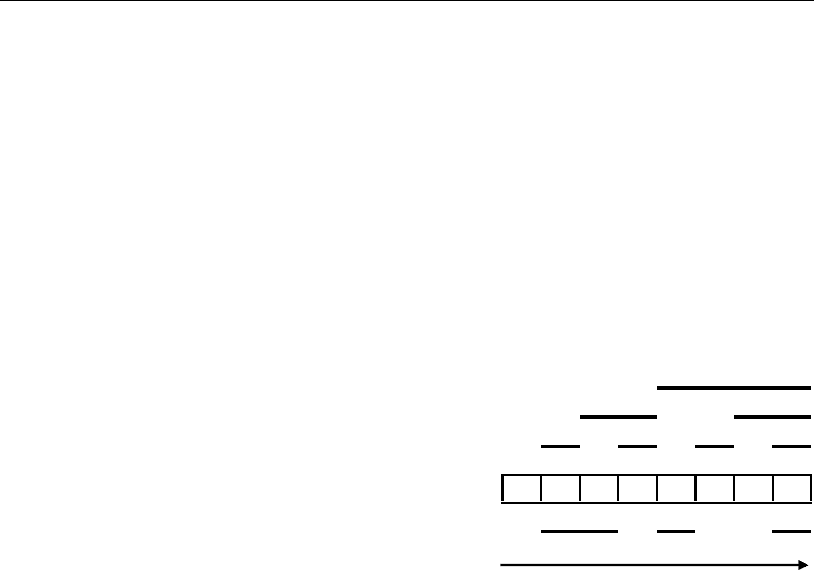
На отрезке конечной длины цифровой «прямой» (рис. 1.1) графически

представлены соотношения между этими

цифровыми множествами.

Определение же бесконечной цифровой

«прямой» следующее: геометрическое изо-

бражение бесконечного множества натураль-

ных действительных чисел N

, когда нату-

ральное число получается последователь-

ным прибавлением 1, начиная с 0, причем 0

является равноправным элементом наряду со

всеми другими цифрами 1, 2, 3 и т.д.

Следовательно, если на бесконечной

«прямой» g заданием начала отсчета и положительного направления цифро-

вого вектора откладывать последовательно единичные отрезки, соответст-

вующие цифрам 0, 1, 2, ... , то каждый единичный отрезок L «прямой» g

однозначно определяется своей координатой N

. Таким образом, каждому

единичному отрезку L «прямой» g соответствует одно действительное нату-

ральное число N

, и обратно: каждому натуральному числу N

соответствует

один элемент, расположенный на конце цифрового вектора.

При таком соответствии каждая последовательность 2

различных набо-

ров значений аргументов с учетом порядка их расположения определяет

принцип кодирования сигналов ОЦК от

0 до (2

– 1) .

Наиболее широкое распространение получило так называемое двоичное

кодирование, которое является основным во всей вычислительной технике.

Исходя из этого, последовательность набора аргументов, соответствующую

двоичному принципу кодирования, будем считать стандартной [24] формой

представления, что и выполнено в табл. 1.1.1 и на рис. 1.1.

При основном двоичном кодировании так же, как и при других способах

кодирования,

можно рассматривать цифровую «прямую» с элементами от 0 до

– 1) как графическое представление системы счисления одного основания,

равного 2

, либо как часть системы счисления с одним основанием, большим

чем 2

. Эту бесконечную «прямую» можно представить также последователь-

ным соединением разрядов числа с меньшими основаниями, равными по зна-

0 1 2 3 4 5 6 7

Рис. 1.1

Глава 1

чению либо различными 2

= 2

... ( K = L + S + T + ...). Такое пред-

ставление числа позволяет изобразить графически каждый аргумент x

и са-

му функцию y = f (x

1 , ... ,

) не только на цифровой «прямой» (одномерное

цифровое пространство), но и в многомерном варианте этого пространства.

Причем каждая координата многомерного цифрового пространства определя-

ется соответствующим разрядом либо группой разрядов числа.

При этом ЛФ y = f (x

1 , ... ,

), принимающая для всех наборов аргумен-

тов x

значение 1*, представляет собой непрерывное цифровое множество

сигналов от 0 до (2

– 1), т.е. то многомерное цифровое пространство Е (уни-

версальное цифровое множество), в котором размещается «объем» любой ЛФ

y = f (x

1 , ... ,

) с меньшим числом наборов аргументов x

, равных 1*.

Для трехместной (тернарной) логической операции y = f (x

, x

) ЛФ,

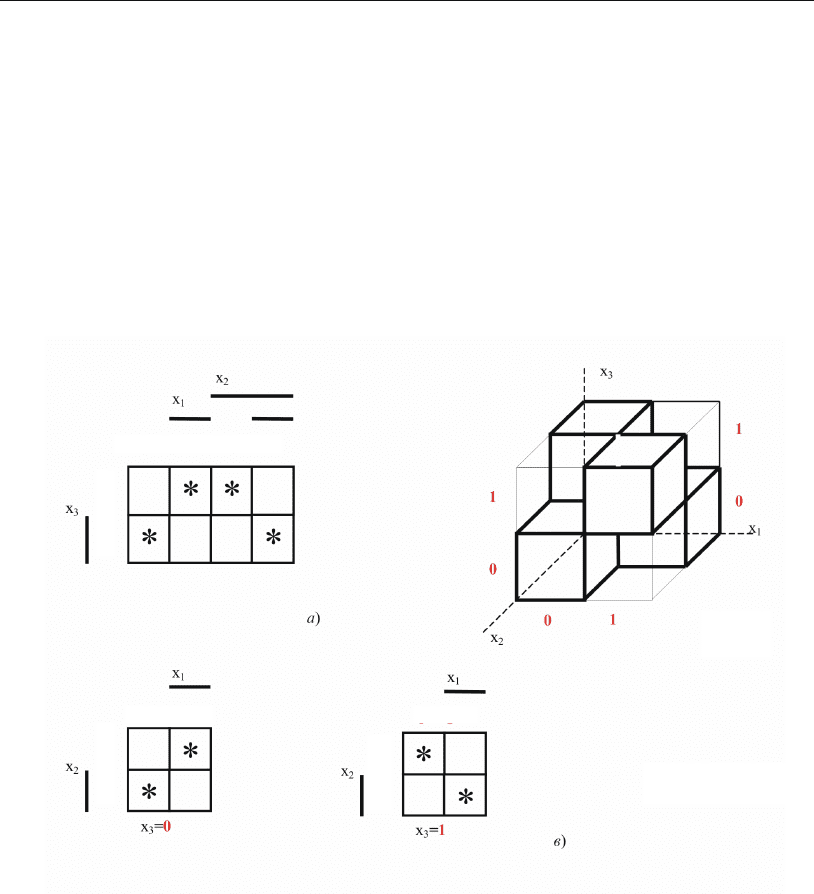
заданная табл. 1.1.1 и представленная (см. рис. 1.1) на цифровой «прямой»

(одномерное пространство), может быть также изображена в двухмерном про-

странстве (см. рис. 1.2, а), трехмерном пространстве (см. рис. 1.2, б) либо в

трехмерном пространстве, нарисованном послойно (см. рис. 1.2, в). В этом

случае можно говорить, что геометрический образ логической функции

y = f (x

1 , ... ,

) одномерного цифрового пространства однозначно может ото-

бражаться на двухмерных и трехмерных цифровых пространствах.

Во всех этих представлениях число ячеек пространства одно и то же, а

число разрядов и их оснований различно. Цифровые пространства с равным

количеством ячеек будем называть эквивалентными. Здесь и в дальнейшем

б)

Рис. 1.2

Основные положения теории

значение ЛФ, равное 1*, обозначим звёздочкой (*), а соответствующая ячейка

пространства, где ЛФ равна 0*, будет пустой.

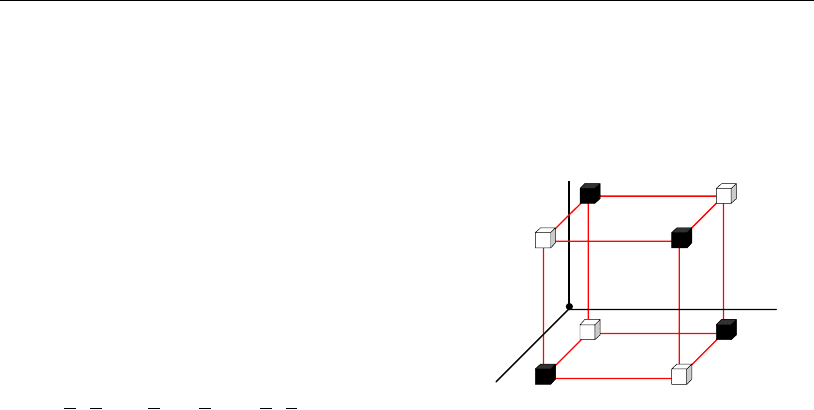
Для того чтобы увидеть все ячейки многомерного цифрового пространст-

ва, уменьшим их масштаб, но сохраним их положение в декартовой системе

координат. Тогда геометрический образ ло-

гической функции рис. 1.2 в трехмерном

цифровом пространстве координат x

, x

будет преобразован в рис. 1.3.

На этих рисунках «длина», «площадь»,

«объем» определяются мерностью про-

странства (одно-, двух-, трех-) и эквива-

лентны друг другу, а также полностью оп-

ределяют логическую функцию

y = x

∨ x

∨

В этом выражении и в дальнейшем ин-

версию функции или аргумента (входными

и выходными сигналами) будем обозначать не верхней чертой над сигналом,

как это обычно выполняется, а нижней. Это нововведение принято нами для

того, чтобы отличать логические функции, полученные из геометрического

представления, от логических функций, которые выводятся аналитическим пу-

тем, исходя из алгебры Буля. Известно, что булева алгебра может быть ис-

пользована только при двоичном принципе кодирования соответствующих ос-

нований позиционных систем счисления и не пригодна при геометрических

принципах кодирования этих оснований систем счисления.

В общем случае можно утверждать, что покрытие (определение термина

«покрытие» приведем ниже) «объема» цифрового множества ЛФ, располо-

женного в многомерном цифровом пространстве, определяет все возможные

варианты построения ЛФ. Здесь следует напомнить, что число таких логиче-

ских функций в научно-технической литературе известно, но подсчет их числа

осуществляется только путем просмотра (или, как говорят, «перебора»). При

этом утверждается, что «уже при сравнительно небольших значениях K (K ≥ 6)

перебор становится практически невозможным даже с использованием вычис-

лительной техники» [25].

Использование геометрического образа логических функций позволяет по-

лучить точный ответ: это число определяется суммой всех возможных сочета-

ний из 2

элементов цифрового множества соответственно по нулю (во мно-

жестве нет логических единиц – пустое множество ∅), по 1 (во множестве со-

держится одна логическая единица), по 2 (в множестве содержится по две ло-

гических единицы) и т.д. вплоть до сочетания из 2

по 2

(в множестве все

элементы равны логической единице – универсальное множество Е).

4 5

7 6

2 3

1 0

Рис. 1.3

Глава 1

Отмеченное записывается следующим образом:

В формуле (1.1.1) первое и последнее слагаемые определяют соответственно

пустое и универсальное множества, сумма которых, как очевидно, равна двум.

Следует отметить, что значения ЛФ могут быть представлены не на всех

возможных наборах значений аргументов, и тогда на некоторых из них они

не определены. Названия таких ЛФ и их «объемов» – неполностью определен-

ные или частичные.

(1.1.1)

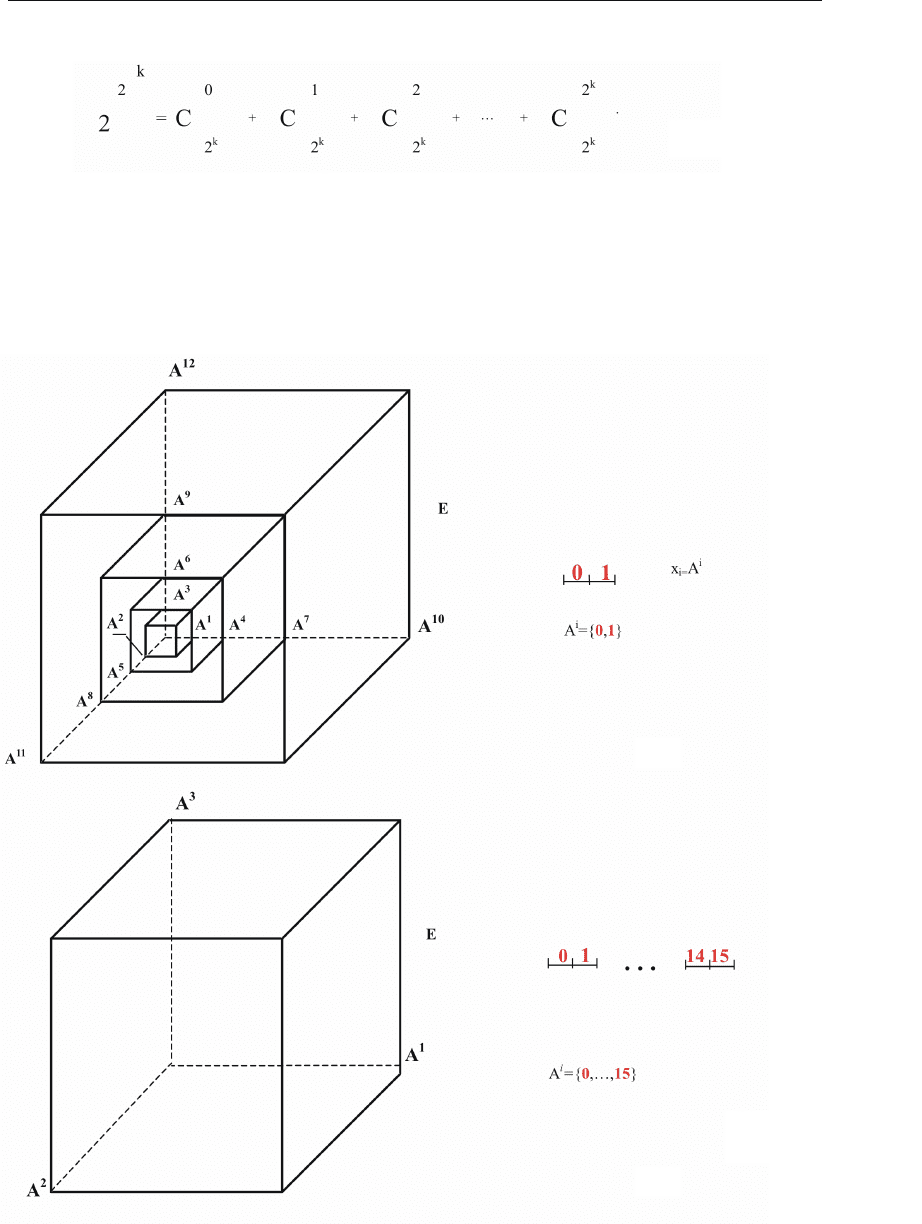
Рис. 1.4 (начало)

а)

б)

Основные положения теории

Для более четкого представления многомерного цифрового пространства,

использующего декартову систему координат, на рис. 1.4, а изображено двена-

дцатимерное цифровое пространство, где каждый разряд имеет основание сис-

темы счисления 2 (цифры 0, 1), а на рис. 1.4, б – эквивалентное ему трехмерное

цифровое множество, где каждый разряд имеет основание системы счисления

16 (цифры 00, ... , 15), которые могут быть, в свою очередь, закодированы раз-

личными способами, например четырьмя разрядами двоичного кода.

Таким образом, для геометрического представления ЛФ может быть вы-

брано цифровое пространство мерности от 1 до K, где все пространство упако-

вывается элементарными фигурами от 0 до (2

– 1) (нумерованное цифровое

пространство). Объединение всех этих 2

элементарных фигур представляет

собой универсальное цифровое множество E, включающее все возможные на-

боры значений K аргументов. Выделение в универсальном множестве E под-

множеств элементарных фигур, соответствующих наборам аргументов, при

которых ЛФ y = f (x

1 , ... ,

) равна 1*, образует ее геометрический образ.

В качестве измерения мерности пространства нами выбрано число разря-

дов соответствующего основания системы счисления, из которых может быть

составлено любое действительное натуральное число N

, нумерующее 2

на-

в)

г)

д)

е)

ж)

Рис. 1.4 (продолжение)

Глава 1

боров аргументов ЛФ. Поэтому геометрический образ многомерного цифрово-

го пространства должен обладать аналогично цифрам разряда свойством замк-

нутости этих цифр на себя. Представить физическое существование одномер-

ного либо двухмерного цифрового пространства, где цифры разрядов, опреде-

ляющих мерность пространства, замкнуты на себя, не сложно. Для одномер-

ного цифрового пространства, «склеивая» между собой свободную грань эле-

ментарного кубика, соответствующего цифре 0 и перпендикулярного свобод-

ной гранью к цифровой оси, со свободной гранью такого же кубика, соответ-

ствующего цифре (2

– 1) и также перпендикулярного свободной гранью к

цифровой оси, получим «полый» тор. Проводя аналогичные «склеивания»

цифр разрядов двухмерного цифрового пространства, получим тор с внутрен-

ней полостью и т.д.

Таким путем может быть получено достаточно сложное тороидальное

многомерное цифровое пространство.

Однако здесь необходимо остановиться и сделать следующее замечание.

Несмотря на то, что декартова система координат и тороидальная являются

ортогональными и имеют взаимно однозначные соответствия [18], обращаться

к более сложной и менее изученной тороидальной системе координат нет не-

обходимости. Такой переход только «затуманит» рассмотрение, а представить

упомянутую выше замкнутость цифр разрядов, т.е. координат на себя, можно

и в декартовой системе координат.

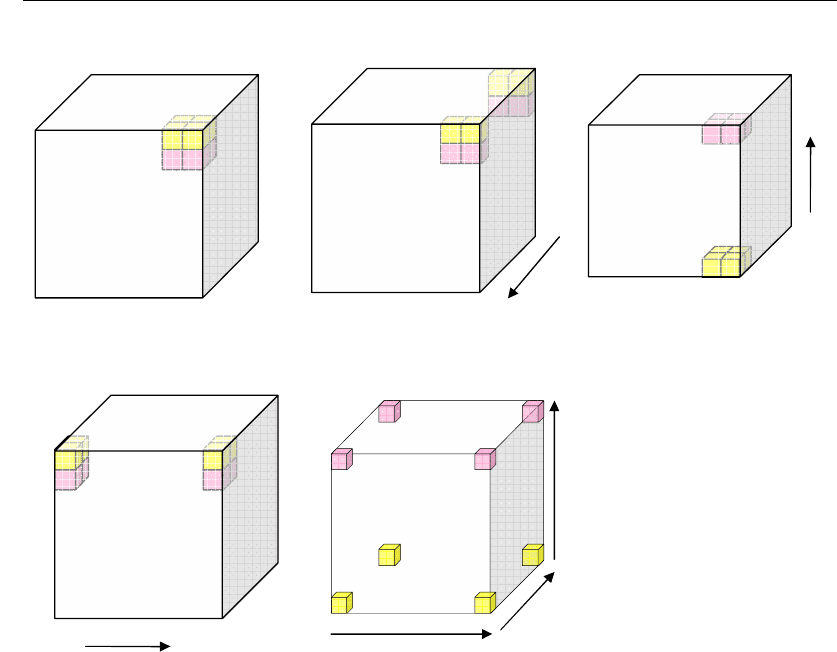
В самом деле, обратимся к трехмерному цифровому пространству декар-

товой системы координат (см. рис. 1.4, в), где на границе этого пространства

расположена геометрическая фигура, состоящая, например, для простоты из-

ложения из восьми элементарных кубиков. Для наглядности дальнейшего из-

ложения половина кубиков имеет более темный цвет.

При сдвиге этой фигуры, которая, как мы условились ранее, является гео-

метрическим образом ЛФ, вдоль координаты A

на одну цифру (см. рис. 1.4, г)

в большую сторону она появится одной своей половинкой в начале координа-

ты A

. Аналогичные положения займет эта фигура при сдвиге на одну цифру

относительно координат A

(см. рис. 1.4, д, е).

Одновременный сдвиг этой фигуры, например, по всем трем координатам

, A

(см. рис. 1.4, ж), приведет к тому, что она будет присутствовать

своими частями в начале и конце всех трех координат.

Здесь следует помнить, что исходная геометрическая фигура (см. рис. 1.4, а)

при любом сдвиге её вдоль координат преобразуется в аналогичные образы (см.

рис. 1.4, г – ж), которые все эквивалентны между собой, т.е. всегда сохраняют

свою форму (не дробятся и не объединяются в более крупные образования) и

всегда при этом находятся внутри многомерного цифрового пространства.

Если при этом многомерное цифровое пространство не бесконечно, а для

основания системы счисления используется циклический код, то отмеченное

выше свойство пространства позволяет сразу сделать важный вывод: число

всех возможных логических функций, представленных формулой (1.1.1), по-

Основные положения теории

требует при наших условиях для своей реализации в n

раз меньше принципи-

альных схем, чем число логических функций формулы (1.1.1).

Это доказывается тем, что циклические перестановки символов (аргумен-

тов) кодового слова вновь приведут к этому кодовому слову. Следовательно,

одна принципиальная схема, эквивалентная исходной логической функции,

при циклической перестановке сигналов на её входах будет эквивалентна n

логическим функциям.

Существуют и другие методы для уменьшения числа принципиальных

схем, реализующих логические функции многомерного цифрового простран-

ства, но это является предметом нашего дальнейшего рассмотрения.

Уже в начале изложения основ теории многомерных цифровых множеств,

где размещаются геометрические образы логических функций, сделаны два

серьёзных вывода. Эти выводы, по нашему мнению, не могли быть получены,

исходя из чисто аналитических логических рассуждений. Это полностью под-

тверждает высказывание Ф. Клейна (F.C. Klein), критикующего чисто фор-

мальную теорию чисел: «Попытка совершенно изгнать созерцание и удержать

только логическое исследование представляется мне в полной мере неосуще-

ствимой. Некоторый остаток, некоторый минимум интуиции всегда должен

сохраниться…». И далее: «…совершенно невозможно чисто логическим путем

показать, что законы, в которых мы обнаружили отсутствие логического про-

тиворечия, действительно имеют силу по отношению к числам, столь хорошо

нам известным эмпирически, что неопределенные объекты могут быть ото-

ждествлены с реальными числами, а выкладки, которые мы над ними произво-

дим, – с реальными эмпирическими процессами» [16].

1.2. Позиционные системы счисления

Позиционные системы счисления занимают основную, главную роль во

всей математике, и их использование при двоичном принципе кодирования ос-

нований имеет в машинной арифметике также всеобщий характер. Тем не менее

использование двоичного кодирования не может определить все возможные ва-

рианты кодирования оснований систем счисления. Нетрудно показать, что чис-

ло кодов, эквивалентных сигналам ОЦК от 0 до (2

– 1) , равно 2

В самом деле, каждой цифре от 0 до (2

– 1) основания системы счисления

сопоставляется его код – слово из алфавита {x

, x

, …, x

}. При двоичном

неизбыточном законе кодирования, например для К = 3, это будут следующие

слова (кодовые комбинации): 0 ↔ x

, 1 ↔ x

, … , 7 ↔ x

. Здесь

цифры 0, … , (2

– 1) и конъюнкции К-го ранга находятся во взаимно одно-

значном соответствии, что определяется постановкой между ними соответст-

вующего знака (↔). Другие взаимно однозначные соответствия могут быть

получены перестановкой конъюнкций К-го ранга.

Обозначим конъюнкции K-го ранга простыми цифрами 0, … , (2

– 1), сов-

падающими с двоичным принципом кодирования. Тогда взаимно однозначные