Кочергин В.И. Теория многомерных цифро-векторных множеств

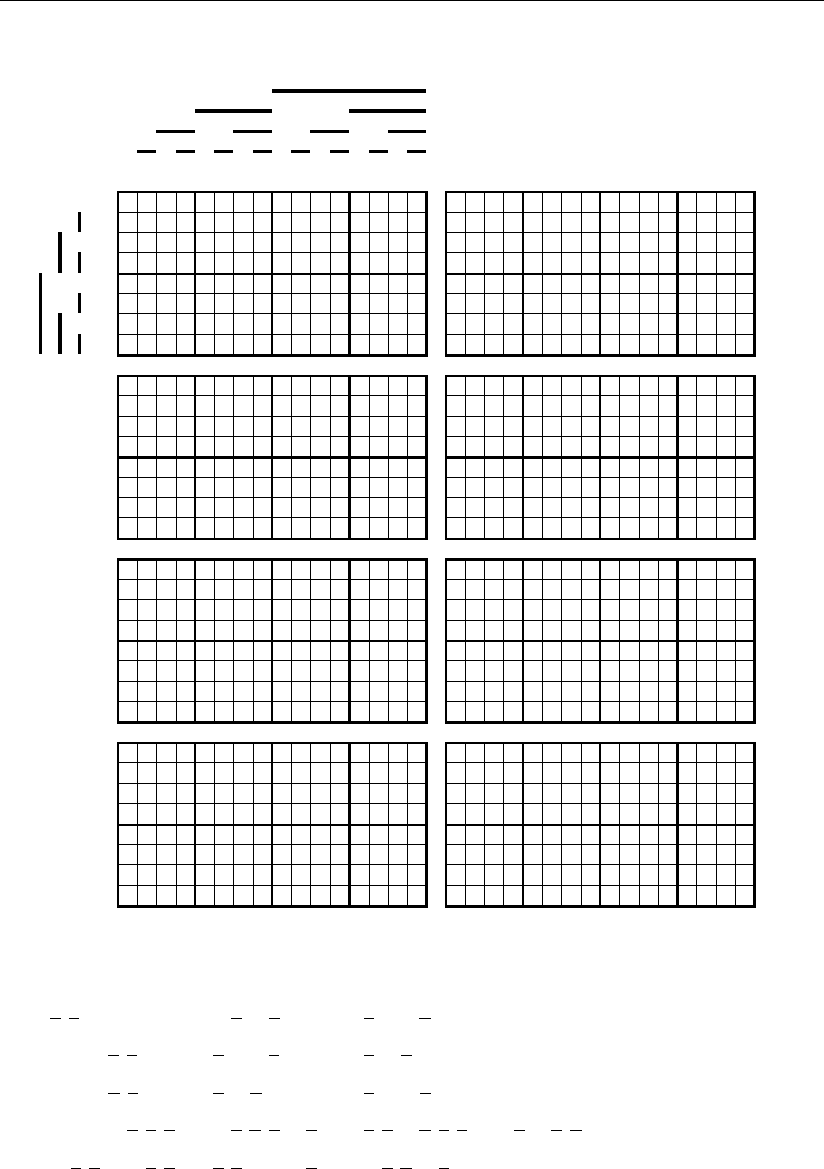
210 Глава 4

a

4

a

3

x′

1

a

2

a

1

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

x

1

0

* *

x

2

1

~

**

~

**

~

*

~

*

~

2

* *

x

3

~

**

~

*

~

**

~

*

~

4

* *

5

*

~

**

~

*

~

*

~

*

~

6

* *

7

~

*

~

**

~

*

~

**

~

* *

~

*

~

*

~

**

~

*

~

*

~

**

*

~

*

~

**

~

*

~

*

~

**

~

**

~

**

~

**

~

Рис. 4.1.5

x′

1

= a

1

a

1

x

1

x

2

∨ a

1

a

2

x

1

x

2

∨

a

1

a

2

x

1

x

2

∨ a

1

a

2

x

1

x

2

∨

∨ a

2

x

1

a

3

a

4

∨ a

2

x

1

a

3

a

4

∨ a

2

x

1

a

3

a

4

∨ a

2

x

1

a

3

a

4

∨

∨ a

1

x

1

x

3

a

4

∨ a

1

x

1

x

3

a

4

∨ a

1

x

1

x

3

a

4

∨ a

1

x

1

x

3

a

4

∨

∨ a

1

a

2

x

2

x

3

a

3

a

4

∨ a

1

a

2

x

2

x

3

a

3

a

4

∨ a

1

a

2

x

2

x

3

a

3

a

4

∨ a

1

a

2

x

2

x

3

a

3

a

4

∨

∨ a

1

a

2

x

2

x

3

a

3

a

4

∨ a

1

a

2

x

2

x

3

a

3

a

4

∨ a

1

a

2

x

2

x

3

a

3

a

4

∨

a

1

a

2

x

2

x

3

a

3

a

4

. (4.1.4)

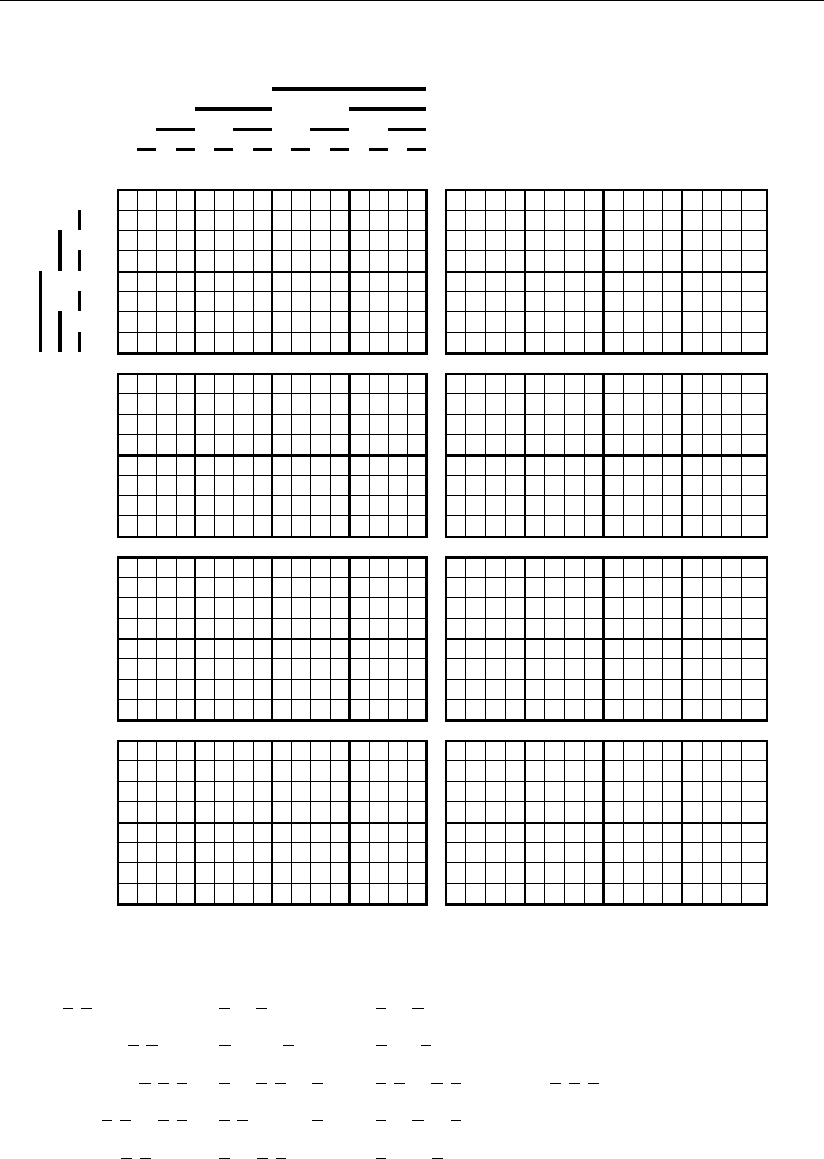
Примеры синтеза комбинационных схем

211

a

4

a

3

x′

2

a

2

a

1

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

x

1

0

**

x

2

1

**

2

~

**

~

**

~

*

~

*

~

x

3

~

**

~

*

~

**

~

*

~

4

**

5

**

6

*

~

**

~

*

~

*

~

*

~

7

~

*

~

**

~

*

~

**

~

**

~

*

~

*

~

*

~

*

~

**

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

Рис. 4.1. 6

x′

2

= a

1

a

2

x

1

x

2

∨ a

1

a

2

x

1

x

2

∨ a

1

a

2

x

1

x

2

∨ a

1

a

2

x

1

x

2

∨

∨ x

1

x

2

a

3

x

3

∨ x

1

x

2

a

3

x

3

∨ x

1

x

2

a

3

x

3

∨ x

1

x

2

a

3

x

3

∨

∨ a

1

a

2

x

1

x

3

a

3

a

4

∨ a

1

a

2

x

1

x

3

a

3

a

4

∨ a

1

a

2

x

1

x

3

a

3

a

4

∨ a

1

a

2

x

1

x

3

a

3

a

4

∨

∨ a

1

a

2

x

1

x

3

a

3

a

4

∨ a

1

a

2

x

1

x

3

a

3

a

4

∨ a

1

a

2

x

1

x

3

a

3

a

4

∨ a

1

a

2

x

1

x

3

a

3

a

4

∨

∨ a

2

x

2

x

3

a

4

∨ a

2

x

2

x

3

a

4

∨ a

2

x

2

x

3

a

4

∨

a

2

x

2

x

3

a

4

. (4.1.5)

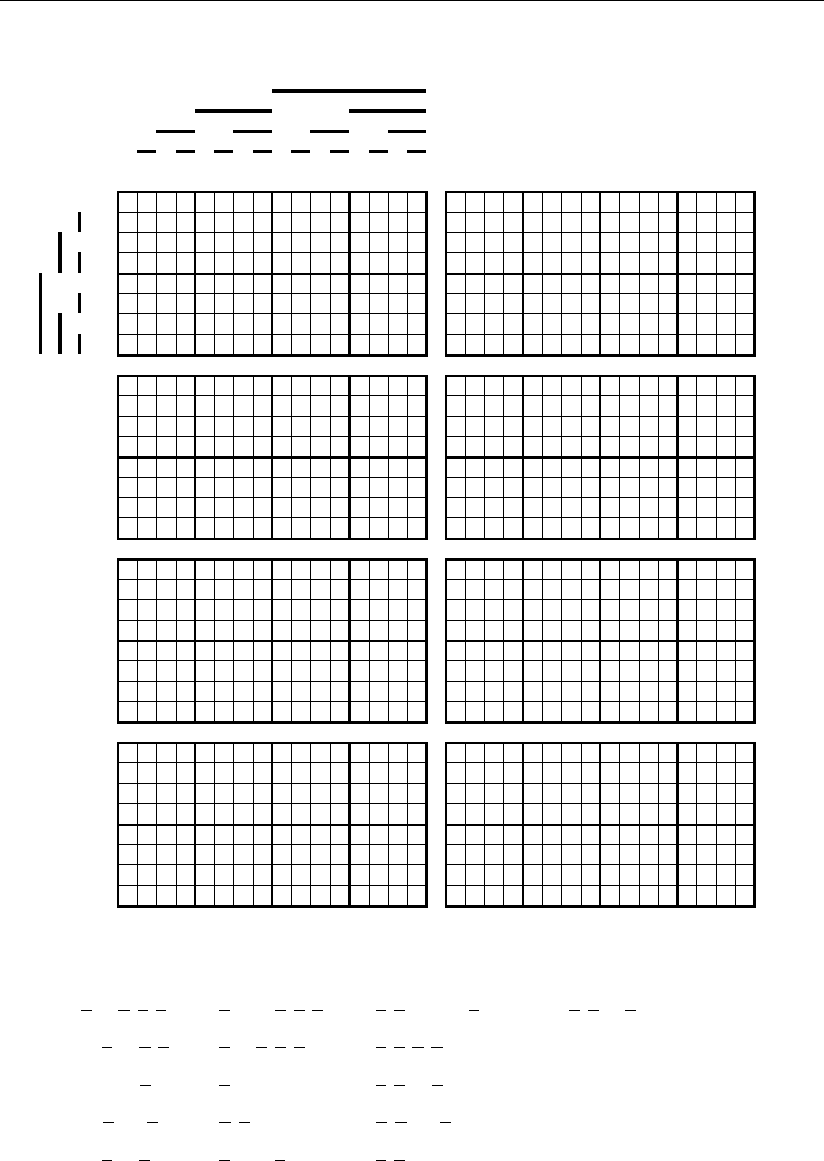
212 Глава 4

a

4

a

3

x′

3

a

2

a

1

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

x

1

0

~

x

2

1

~

2

~

x

3

~

4

******

~

***

~

***

~

5

**

~

** ***

~

**** *

~

6

*

~

**** ***

~

** **

~

7

***

~

***

******

~

*

~

**

~

*

~

**

~

**

~

*

~

**

~

*

~

**

~

***

~

*

~

*

~

**

*

~

**

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

Рис. 4.1.7

x′

3

= a

1

a

2

x

1

x

2

a

3

a

4

∨ a

1

a

2

x

1

x

2

a

3

a

4

∨ a

1

a

2

x

1

x

2

a

3

a

4

∨ a

1

a

2

x

1

x

2

a

3

a

4

∨

∨ a

1

a

2

x

1

x

2

a

3

a

4

∨ a

1

a

2

x

1

x

2

a

3

a

4

∨ a

1

a

2

x

1

x

2

a

3

a

4

∨ a

1

a

2

x

1

x

2

a

3

a

4

∨

∨ a

2

x

2

x

3

a

4

∨ a

2

x

2

x

3

a

4

∨ a

2

x

2

x

3

a

4

∨ a

2

x

2

x

3

a

4

∨

∨ x

1

x

2

x

3

a

3

∨ x

1

x

2

x

3

a

3

∨ x

1

x

2

x

3

a

3

∨ x

1

x

2

x

3

a

3

∨

∨ a

1

a

2

x

3

a

3

∨ a

1

a

2

x

3

a

3

∨ a

1

a

2

x

3

a

3

∨

a

1

a

2

x

3

a

3

. (4.1.6)

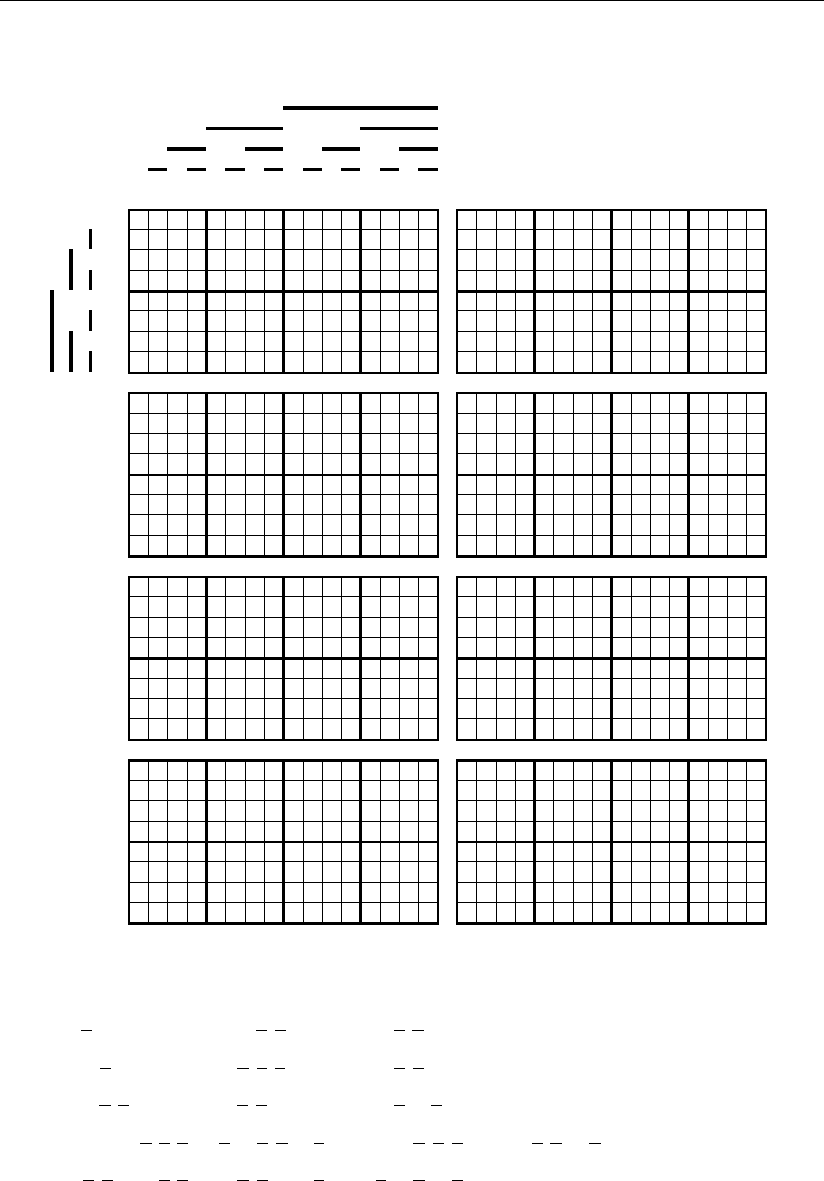
Примеры синтеза комбинационных схем

213

a

4

a

3

a′

1

a

2

a

1

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

x

1

0

~

*

~

**

~

*

~

x

2

1

~

**

~

*

~

*

~

2

~

*

~

**

~

*

~

x

3

**

~

*

~

*

~

4

*

~

**

~

*

~

5

~

**

~

*

~

*

~

6

*

~

*

~

*

~

*

~

7

*

~

*

~

**

~

*

~

*

~

**

~

**

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

Рис. 4.1.8

a′

1

= a

1

a

2

x

1

x

2

∨ a

1

a

2

x

1

x

2

∨ a

1

a

2

x

1

x

2

∨ a

1

a

2

x

1

x

2

∨

a

1

x

2

a

3

a

4

∨ a

1

x

2

a

3

a

4

∨ a

1

x

2

a

3

a

4

∨ a

1

x

2

a

3

a

4

∨

a

1

a

2

x

3

a

3

∨ a

1

a

2

x

3

a

3

∨ a

1

a

2

x

3

a

3

∨ a

1

a

2

x

3

a

3

∨

∨ a

2

x

1

x

2

x

3

a

3

a

4

∨ a

2

x

1

x

2

x

3

a

3

a

4

∨ a

2

x

1

x

2

x

3

a

3

a

4

∨ a

2

x

1

x

2

x

3

a

3

a

4

∨

∨ a

2

x

1

x

2

x

3

a

3

a

4

∨ a

2

x

1

x

2

x

3

a

3

a

4

∨ a

2

x

1

x

2

x

3

a

3

a

4

∨

a

2

x

1

x

2

x

3

a

3

a

4

. (4.1.7)

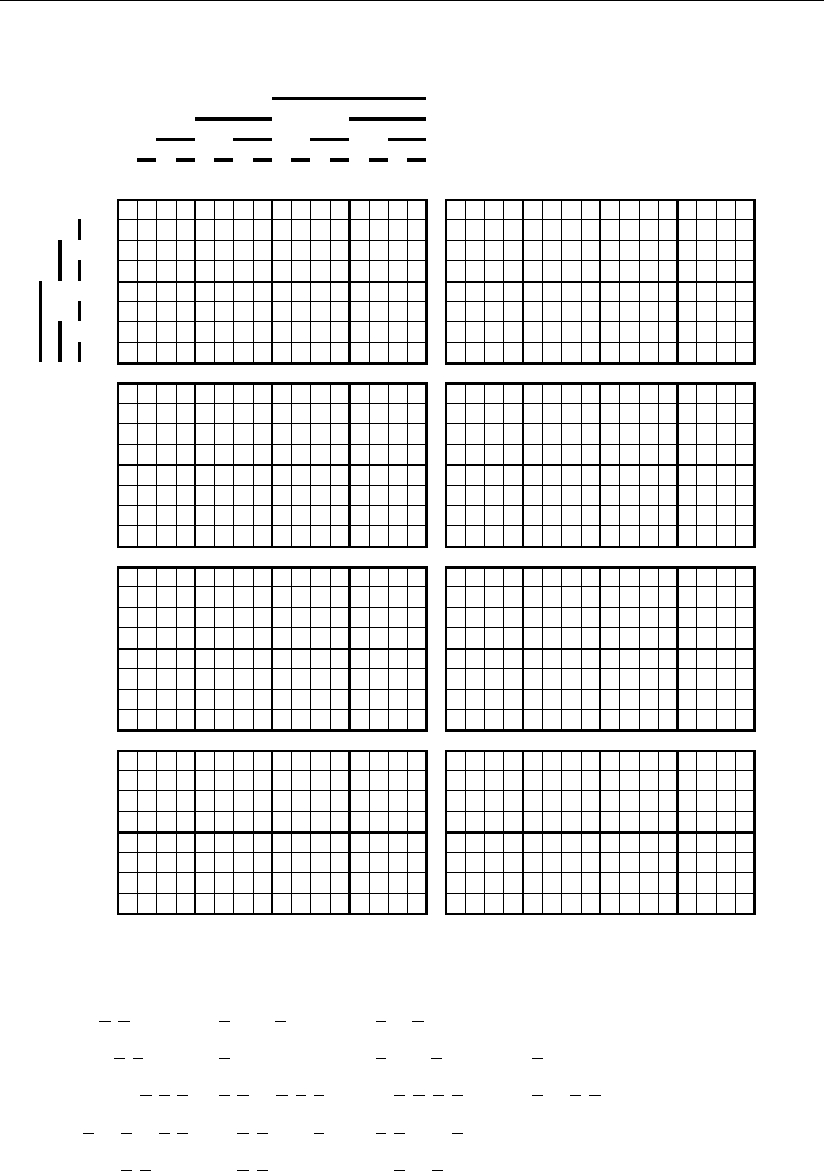
214 Глава 4

a

4

a

3

a′

2

a

2

a

1

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

x

1

0

~

*

~

**

~

*

~

x

2

1

~

*

~

**

~

*

~

2

~

**

~

*

~

*

~

x

3

**

~

*

~

*

~

4

*

~

**

~

*

~

5

*

~

*

~

*

~

*

~

6

~

**

~

*

~

*

~

7

*

~

**

~

**

~

*

~

*

~

*

~

*

~

**

~

**

~

*

~

*

~

*

~

*

~

*

**

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

Рис. 4.1.9

a′

2

= a

1

a

2

x

1

x

2

∨ a

1

a

2

x

1

x

2

∨ a

1

a

2

x

1

x

2

∨ a

1

a

2

x

1

x

2

∨

∨a

1

a

2

x

3

a

3

∨ a

1

a

2

x

3

a

3

∨ a

1

a

2

x

3

a

4

∨ a

1

a

2

x

3

a

4

∨

∨ a

1

x

1

x

2

x

3

a

3

a

4

∨ a

1

x

1

x

2

x

3

a

3

a

4

∨ a

1

x

1

x

2

x

3

a

3

a

4

∨ a

1

x

1

x

2

x

3

a

3

a

4

∨

∨ a

1

x

1

x

2

x

3

a

3

a

4

∨ a

1

x

1

x

2

x

3

a

3

a

4

∨ a

1

x

1

x

2

x

3

a

3

a

4

∨ a

1

x

1

x

2

x

3

a

3

a

4

∨

∨ a

2

x

2

x

3

a

4

∨ a

2

x

2

x

3

a

4

∨ a

2

x

2

x

3

a

4

∨

a

2

x

2

x

3

a

4

. (4.1.8)

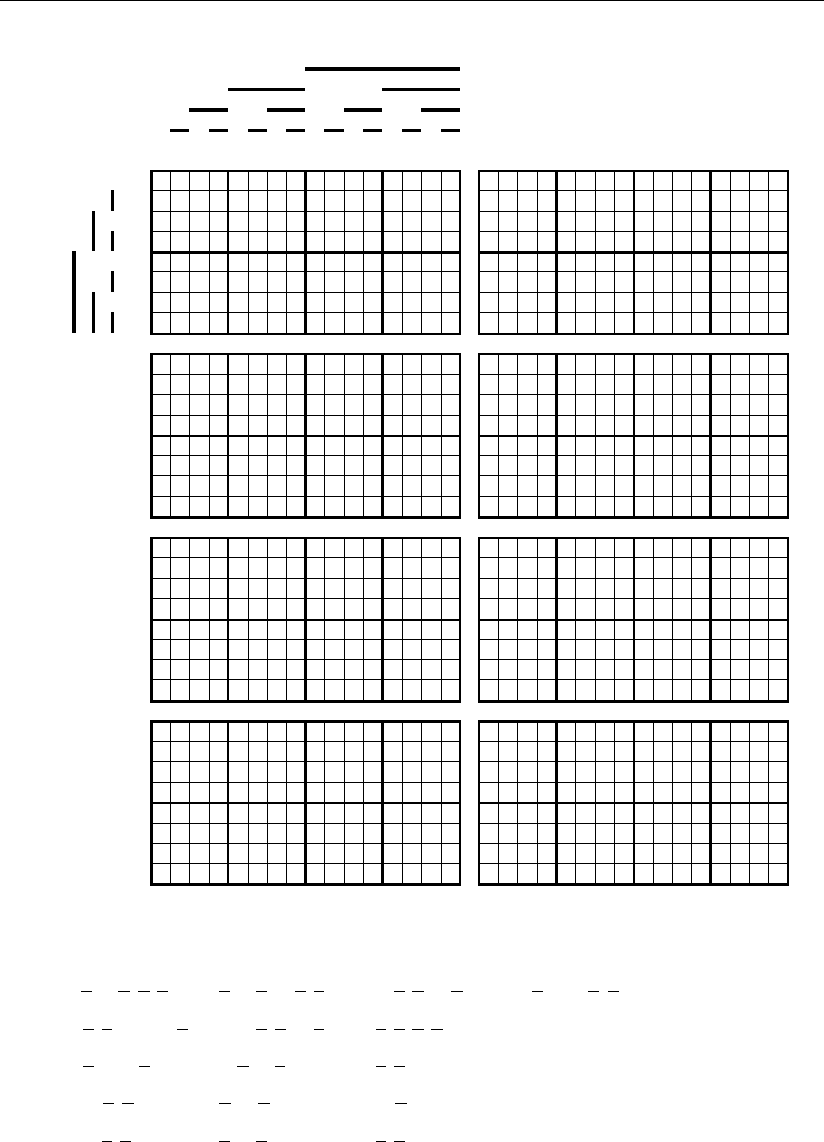
Примеры синтеза комбинационных схем

215

a

4

a

3

a′

3

a

2

a

1

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

x

1

0

*** ***

x

2

1

~

*

~

**

~

**

~

*

~

2

~

**

~

*

~

*

~

**

~

x

3

***

4

~

***

~

***

~

5

** * * **

6

***

** *

7

~

***

~

***

~

*

~

*

~

**

~

**

~

**

~

**

~

*

~

**

~

**

~

**

~

*

~

*

~

**

~

**

~

*

~

*

~

*

~

**

~

*

~

*

~

Рис. 4.1.10

a′

3

= a

1

a

2

x

1

x

2

x

3

a

4

∨ a

1

a

2

x

1

x

2

x

3

a

4

∨ a

1

a

2

x

1

x

2

x

3

a

4

∨ a

1

a

2

x

1

x

2

x

3

a

4

∨

∨ a

1

a

2

x

1

x

2

x

3

a

4

∨ a

1

a

2

x

1

x

2

x

3

a

4

∨ a

1

a

2

x

1

x

2

x

3

a

4

∨ a

1

a

2

x

1

x

2

x

3

a

4

∨

∨ a

2

x

1

a

3

a

4

∨ a

2

x

1

a

3

a

4

∨ a

2

x

1

a

3

a

4

∨ a

2

x

1

a

3

a

4

∨

∨ x

1

x

2

x

3

a

3

∨ x

1

x

2

x

3

a

3

∨ x

1

x

2

x

3

a

3

∨ x

1

x

2

x

3

a

3

∨

∨ a

1

a

2

x

3

a

3

∨ a

1

a

2

x

3

a

3

∨ a

1

a

2

x

3

a

3

∨

a

1

a

2

x

3

a

3

. (4.1.9)

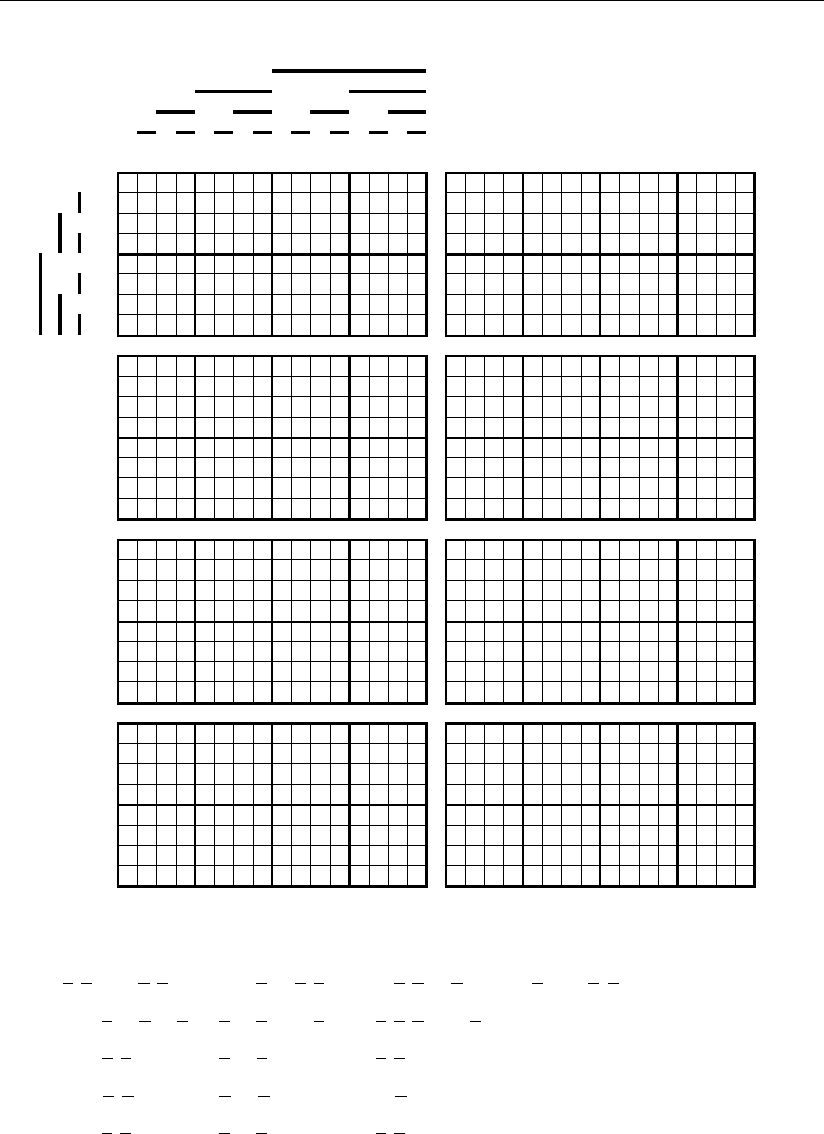
216 Глава 4

a

4

a

3

a′

4

a

2

a

1

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

x

1

0

~

**

~

****

~

x

2

1

~

*****

~

*

~

2

~

*****

~

*

~

x

3

~

** ****

~

4

~

****

~

**

~

5

~

*

~

*****

~

6

~

*

~

*****

~

7

~

****

**

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

**

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

**

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

*

~

Рис. 4.1.11

a′

4

= a

1

a

2

x

1

x

2

x

3

a

3

∨ a

1

a

2

x

1

x

2

x

3

a

3

∨ a

1

a

2

x

1

x

2

x

3

a

3

∨ a

1

a

2

x

1

x

2

x

3

a

3

∨

∨ a

1

a

2

x

1

x

2

x

3

a

3

∨ a

1

a

2

x

1

x

2

x

3

a

3

∨ a

1

a

2

x

1

x

2

x

3

a

3

∨ a

1

a

2

x

1

x

2

x

3

a

3

∨

∨ a

1

x

2

a

3

a

4

∨ a

1

x

2

a

3

a

4

∨ a

1

x

2

a

3

a

4

∨ a

1

x

2

a

3

a

4

∨

∨ x

1

x

2

x

3

a

3

∨ x

1

x

2

x

3

a

3

∨ x

1

x

2

x

3

a

3

∨ x

1

x

2

x

3

a

3

∨

∨ a

1

a

2

x

3

a

3

∨ a

1

a

2

x

3

a

3

∨ a

1

a

2

x

3

a

3

∨

a

1

a

2

x

3

a

3

. (4.1.10)

Примеры синтеза комбинационных схем

217

Покрытие геометрических образов цифровых сигналов разрядов x′

1

, x′

2

, x′

3

,

a′

1

,

a′

2

, a′

3

,

a′

4

представлено на рис. 4.1.5 – 4.1.11, где это реализовано движением

«сверху вниз». Для большей прозрачности синтеза в каждом из этих рисунков

приведено два столбца геометрических образов. В первом левом столбце пока-

зано последовательное покрытие подмножествами конкретного геометрическо-

го образа цифровых сигналов разрядов систематического кода, а в правом –

изображены геометрические образы покрывающих их подмножеств, где их

ячейки отмечены знаком ~. В результате покрытия конкретного геометрическо-

го образа подмножеством, расположенным с ним на одной горизонтали, знак

звездочки в геометрическом образе заменяется знаком ~, а измененный таким

образом геометрический образ переходит во все нижние его представления

первого столбца. Это движение осуществляется до тех пор, пока в геометриче-

ском образе все звездочки не будут заменены знаком ~.

В первом столбце всех подмножеств, которые в общем случае являются

элементарными и поэтому весьма прозрачными для записи в аналитическом

виде, представлены элементы логических сумм для аналитической записи кон-

кретного геометрического образа цифровых сигналов исправленных разрядов

систематического кода.

Логические выражения (4.1.4) – (4.1.10) полностью определяют выполне-

ние двухуровневого декодирующего устройства, обладающего максимально

возможным быстродействием.

Рассмотрев этот пример, видим что его можно значительно упростить. Из

геометрических образов исправленных сигналов разрядов a′

1

, a′

2

, a′

3

, представ-

ленных на с. 206, видно, что соответствующими мысленными поворотами от-

носительно конкретных осей симметрии цифрового пространства можно полу-

чить геометрические образы сигналов разрядов x′

1

, x′

2

, x′

3

.

Для разрядов a′

1

, a′

2

однократные повороты относительно оси 2 двухмерно-

го цифрового пространства координат A(a

1

, a

2

), X(x

1

, x

2

) позволяют получить

геометрические образы сигналов контрольных разрядов x′

1

, x′

2

. Эти преобразо-

вания распространяются и на соответствующие логические функции, где долж-

ны быть осуществлены следующие замены:

a′

1

(a

1

, a

2

, a

3

, a

4

, x

1

, x

2

, x

3

) → x′

1

= a′

1

(x

1

, x

2

, a

3

, a

4

, a

1

, a

2

, x

3

);

a′

2

(a

1

, a

2

, a

3

, a

4

, x

1

, x

2

, x

3

) → x′

2

= a′

2

(x

1

, x

2

, a

3

, a

4

, a

1

, a

2

, x

3

).

Для разряда a′

3

последовательные повороты первоначально относительно

оси 2 двухмерного цифрового пространства координат A(a

1

, a

2

, a

3

), X(x

1

, x

2

, a

3

)

выполняются следующей заменой:

a′

3

(a

1

, a

2

, a

3

, a

4

, x

1

, x

2

, x

3

) → x*

3

= a′

3

(x

1

, x

2

, x

3

, a

4

, a

1

, a

2

, a

3

)

и дают промежуточный геометрический образ логической функции, а второй

поворот относительно оси 2 двухмерного цифрового пространства координат

a

1

, a

2

либо координат x

1

, x

2

позволяет получить геометрический образ исправ-

ленного сигнала контрольного разряда x′

3

.

218 Глава 4

Эти двойные преобразования представляются следующими схемами замен

координат:

a′

3

(a

1

, a

2

, a

3

, a

4

, x

1

, x

2

, x

3

) → x*

3

= a′

3

(x

1

, x

2

, x

3

, a

4

, a

1

, a

2

, a

3

) → x′

3

= x*

3

(x

2

, x

1

, x

3

,

a

4

, a

1

, a

2

, a

3

) либо a′

3

(a

1

, a

2

, a

3

, a

4

, x

1

, x

2

, x

3

) → x*

3

= a′

3

(x

1

, x

2

, x

3

, a

4

, a

1

, a

2

, a

3

) →

→ x′

3

= x*

3

(x

1

, x

2

, x

3

, a

4

, a

2

, a

1

, a

3

),

что комплексно представляется двумя вариантами:

Вариант 1

a

1

→ x

2

a

2

→ x

1

x

1

→ a

1

x

2

→ a

2

Вариант 2

a

1

→ x

1

a

2

→ x

2

a

3

↔ x

3

x

1

→ a

2

x

2

→ a

1

Эти геометрические преобразования выглядят следующим образом:

*

*** * * * ** ***

**

**** *

***

** *

*** * *

**

*

**** *

*** * *

** *

***

** *

**

***

** *

**

*

***

* * * ** *** **

*

**** *

** ** *

** *

**

* * *

**

*

** *

*** * *

**

a′

1

** *

**

***

a′

2

** *

**

***

↓ x′

1

↓ x′

2

*

* *

*

***** ***** *** *

**

*

****** **** ** **

**** ** ** **** ** **** **** ***** *

*

* * *

*** **** ** **

*** *

*

*** ***** *** *

***

x′

1

**** ***** *****

x′

2

** ** **** ******

***

*** * *

*** **

**** *

*

**** *

*** **

*

***

*

***** * * *** ******* *** * ***

** * * ** ** **** **** ** **

***

** * *** ** **** **** *

a′

3

* * ***

*****

x*

3

→

*** * ***

*******

↓ x′

3

*

******* *** * ***

*** ** **** **** *

* * **** **** ** **

*** * ***

*******

Примеры синтеза комбинационных схем

219

Пример 2. Синтез устройства исправления одиночных ошибок двоичной

системы счисления для любых синтезированных кодов основания n = 2

4

Примеры синтеза быстродействующих арифметических и логических уст-

ройств, использующие методы многомерных цифровых множеств и представ-

ленные в [1– 3], относятся к методам точных математических моделей и не

требуют дополнительных пояснений. Другие примеры в [4–6], решающие зада-

чи исправления всех одиночных ошибок в системах счисления основания

n = 16, опираются на эвристический метод решения задачи, который обычно

противопоставляется в математике формальным методам решения, опираю-

щимся на точные математические модели.

Известно, что использование эвристик сокращает время решения задачи по

сравнению с методом полного направленного перебора возможных алгоритмов

и относится к множеству допустимых решений. Подобным образом нами было

синтезировано геометрическим эвристическим способом 18 кодов, исправляю-

щих одиночные ошибки в любых логических устройствах и блоках машинной

арифметики. Несмотря на принятые нами в этом синтезе ограничения, которые

заключаются в использовании здесь только дружественных кодов в информа-

ционной и контрольной его частях, на основе этих примеров можно сделать

следующие обобщающие выводы: для устройств исправления одиночных оши-

бок все 18 кодов полностью равноценны в смысле затрат оборудования и быст-

родействия; при схемной реализации конкретной логической или математиче-

ской функции в этих кодах имеется один или несколько кодов, позволяющих

получить решения, оптимальные по затратам оборудования.

Следует заметить, что в этих синтезированных нами кодах использована

многозначная логика, когда в ячейках многомерного цифрового пространства

для информационной части кода располагаются не логические значения нуль

(0*) или единица (1*), а цифровые значения 0–7 контрольной его части. Тем

самым получается геометрический образ логической функции синтезированно-

го систематического кода в четырехмерном цифро-векторном пространстве.

Для решения задачи синтеза устройства исправления одиночных ошибок

любого систематического кода основания n =2

4

нужно определить все эти коды.

Необходимо отметить, что уже на начальных этапах исследований совершен-

ных кодов высказывалось мнение [7], что «имеются некоторые результаты,

показывающие, что совершенных кодов мало, и кажется вполне правдоподоб-

ным, что не существует других совершенных кодов», кроме известных в это

время. Ошибочность этого утверждения представим в данном примере.

Очевидно, что к геометрическому образу любого из уже известных кодов

можно применить мысленные повороты относительно осей симметрии цифро-

векторного пространства и получить, таким образом, все другие эквивалентные

коды, исправляющие, например, все одиночные ошибки.

В первой главе было выведено число возможных положений геометриче-

ских образов логических функций s

i

= 2

i

i!, где i – мерность цифрового про-

странства, совпадающая с числом разрядов двоичного кода.

Кочергин В.И. Теория многомерных цифро-векторных множеств

Подождите немного. Документ загружается.