Кочергин В.И. Теория многомерных цифро-векторных множеств
Подождите немного. Документ загружается.

Глава 3
190
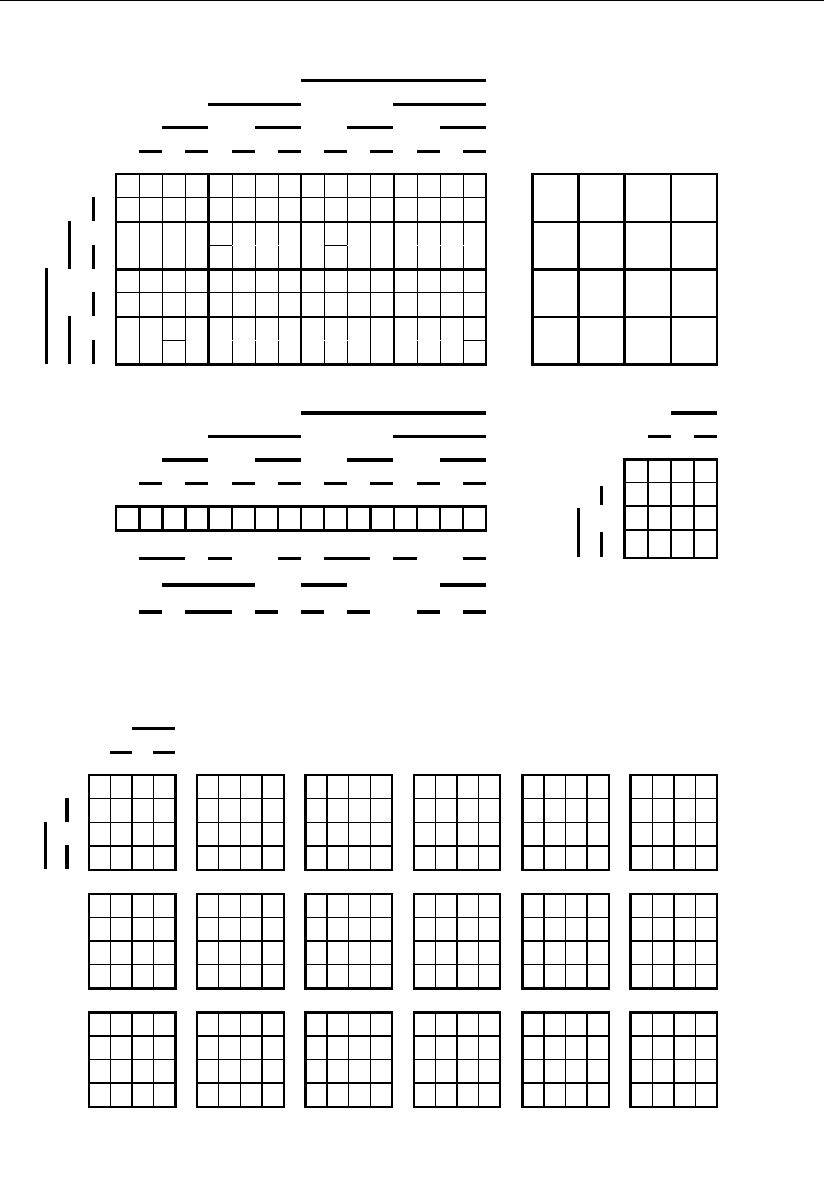
Рис. 3.65
a
1
x
3
x
2
x
1
a
2
0
0 0 2 0 1 8 4 0 1 5 9 1
1
3 1
a
3
0 2 2
2
6 10 3 2 11 7 3 2 3 1
3
3
µ
1
µ
2
0 12 5 4 6 4 4
4
5 7
5
5 13 1 5 4
a
4
6 7 14 2
6
6 6 4 7
7
5 7 6 7 3 15
µ
4
µ
3
0 12 8 9 8 10
8
8 11 9 9
9
13 1 8 9
11 10 14 2 10
10
8 10
11
11 11 9 11 10 3 15
µ
3
µ
4
12
12
14 12 13 12 8 4 13 12 5 9
13
13 13 15
14 12
14
14 6 10 14 15 11 7 14 15 13 15 15
15
µ
2
µ
1
a
4
a
2
a
3
a
1
a
2
a
1
a
3
0 5 3 6
a
4
7
2
4 1
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
6 3 5 0
1 4 2 7
x
1
x
2
x
3
a
2
a
1
Первый класс кодов
a
3
0 7 3 4 0 7 5 2 0 7 3 4 0 7 6 1 0 7 6 1
*
0 7 5 2
a
4
5 2 6 1 3 4 6 1 6 1 5 2 3 4 5 2 5 2 3 4 6 1 3 4
6 1
5 2 6 1 3 4 5 2 6 1 5 2 3 4 3 4 5 2 3 4 6 1
3 4
0 7 5 2 0 7 3 4 0 7 6 1 0 7 6 1 0 7 5 2 0 7
Вто
р
ой класс ко
д
ов
0 6 3 5 0 6 5 3 0 5 3 6 0 5 6 3 0 3 6 5 0 3 5 6
5 3
6 0 3 5 6 0 6 3 5 0 3 6 5 0 5 6 3 0 6 5 3 0
7 1
4 2 7 1 2 4 7 2 4 1 7 2 1 4 7 4 1 2 7 4 2 1
2 4
1 7 4 2 1 7 1 4 2 7 4 1 2 7 2 1 4 7 1 2 4 7
Т
р
етий класс ко
д
ов
0 5 3 6 0 3 5 6 0 6 3 5 0 3 6 5 0 5 6 3 0 6 5 3
7 2
4 1 7 4 2 1 7 1 4 2 7 4 1 2 7 2 1 4 7 1 2 4
6 3
5 0 6 5 3 0 5 3 6 0 5 6 3 0 3 6 5 0 3 5 6 0
1 4
2 7 1 2 4 7 2 4 1 7 2 1 4 7 4 1 2 7 4 2 1 7
x
1
x
2
x
3
x
1
x
3
x
2
x
2
x
1
x
3
x
2
x
3
x
1
x
3
x
2
x
1
x
3
x
1
x
2
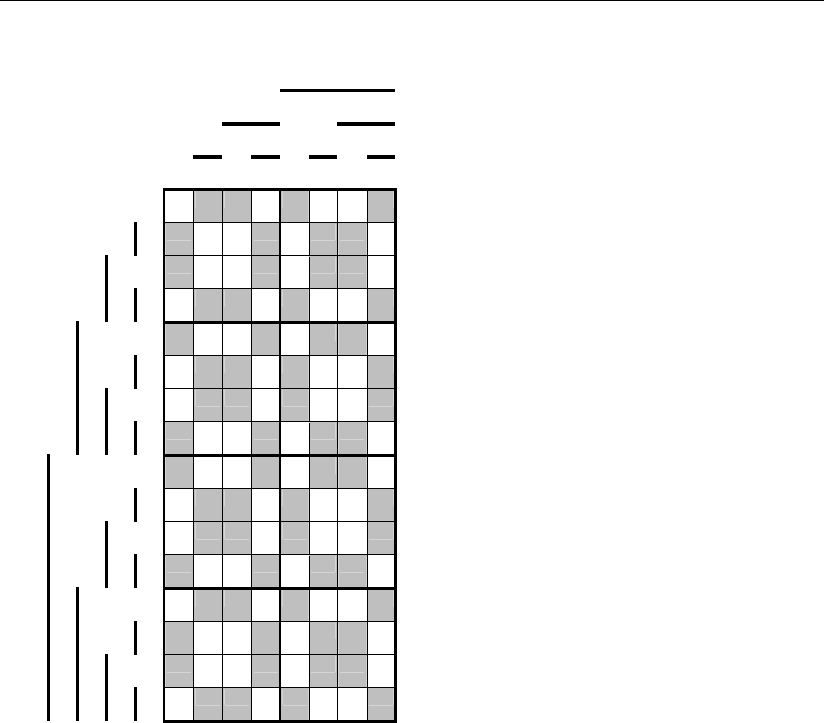
Рис. 3.66
Контролеспособность позиционных систем счисления
191
Сравнение распределения цифр 0–7 контрольных разрядов в многомер-
ном цифровом пространстве информационной части кода с аналогичным рас-
пределением кодов оснований n = 4, 8 показывает, что полностью контроле-
способный код основания n = 16 определяет все соотношения между инфор-
мационной и контрольной частями в кодах меньших оснований. Поэтому в
дальнейшем будем рассматривать только такие основания систем счисления,
которые позволяют синтезировать полностью контролеспособные коды.
3.7.3. Коды больших оснований систем счисления
с исправлением одиночных ошибок
Синтез кодов больших оснований систем счисления можно выполнить,
опираясь на представленную выше систему счисления основания n = 16. При
этом процедура операции синтеза будет так же, как рассмотренная выше, за-
ключаться в размещении в многомерном цифровом пространстве информаци-
онных и одного контрольного разряда фигур основания n = 16 семимерного
цифрового пространства (см. рис. 3.53), где реализовано исправление одиноч-
ных ошибок.
Для сокращения графическо-
го материала ограничим рас-
смотрение только представлени-
ем синтеза кода одного класса.
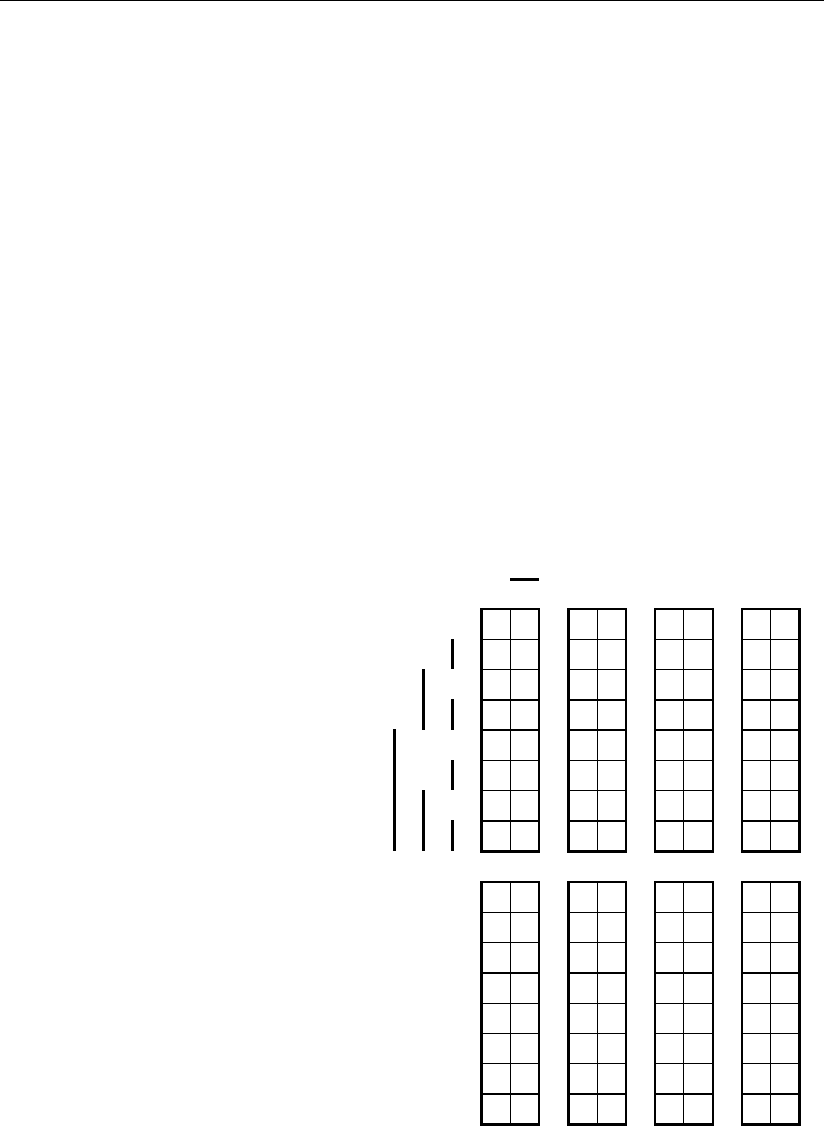
На рис. 3.67 приведены эти
восемь ячеек семимерного про-
странства, которые вместе с раз-
мещенными в них фигурами обо-
значены σ
1
– σ
8
. Эти фигуры ох-
ватывают все варианты разме-
щения цифр 0–15 основания n =
16 в семимерном (k = 3, i = 4)
цифровом пространстве, где ис-
правляются все одиночные
ошибки. Построение этих фигур,
выполненное аналогично осно-
ванию n = 2, определяется после-
довательным размещением этих
цифр на цифровой прямой емко-
стью 2
7
с сохранением симмет-
рии размещения относительно
центра этой прямой и неизмен-
ности кодового расстояния меж-
ду ними, обеспечивающим ис-
правление одиночных ошибок.
x
3
a
2
µ
1
µ
2
µ
3
µ
4
a
3
µ
2
µ
1
µ
4
µ
3
µ
3
µ
4
µ
1
µ
2
a
4
µ
4
µ
3
µ
2
µ
1
µ
4
σ
1
µ
3
σ
2
µ
2
σ
3
µ
1
σ
4
µ
3
µ
4
µ
1
µ
2
µ
2
µ
1
µ
4
µ
3
µ
1
µ
2
µ
3
µ
4
µ
1
µ
2
µ
3
µ
4
µ
2
µ
1
µ
4
µ
3
µ
3
µ
4
µ
1
µ
2
µ
4
σ
5
µ
3
σ
6
µ
2
σ
7
µ
1
σ
8
µ
4
µ
3
µ
2
µ
1
µ
3
µ
4
µ
1
µ
2
µ
2
µ
1
µ
4
µ
3
µ
1
µ
2
µ
3
µ
4
Рис. 3.67
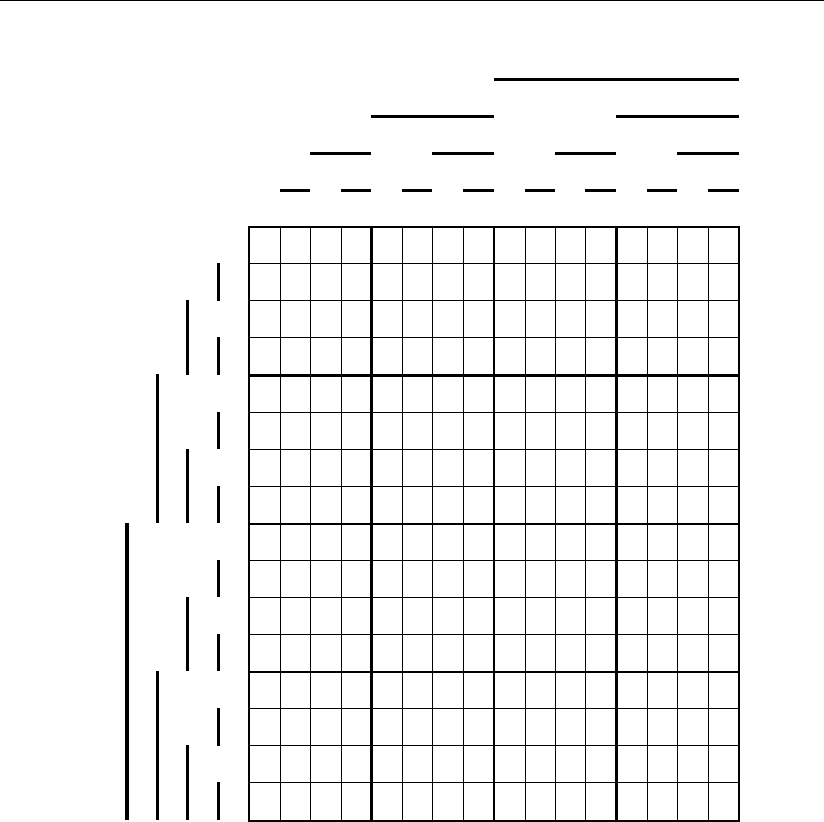
Глава 3
192
Опустив достаточно прозрачные из изложенного выше операции подстановки
фигур σ
1
– σ
8
в ячейки пространства большей мерности (см. рис. 3.53), на
рис. 3.68 приведен один из многочисленных вариантов такого размещения в про-
странстве λ
8
(0), что определяет полностью контролеспособный код для основания
n = 2
11
. В соответствии с этой процедурой не представит какого-либо труда раз-
местить в ячейках многомерного цифрового пространства информационной части
кода эквивалентные контрольным сигналам разрядов x
1
– x
4
цифры 0–15.
Для компактного графического представления одного из вариантов синтеза на
рис. 3.69,а показаны большие ячейки информационного пространства, которые
обозначены соответственно s
1
– s
4
и s
1
– s
4
, а на рис. 3.69, б приведена ячейка s
1
с
заполненными элементарными ячейками информационного пространства эквива-
лентными цифрами контрольной части синтезированного кода.
a
11
a
10
a
9
x
4
σ
1
σ
2
σ
3
σ
4
σ
4
σ
3
σ
2
σ
1
a
5
σ
5
σ
6
σ
7
σ
8
σ
8
σ
7
σ
6
σ
5
a
6
σ
6
σ
5
σ
8
σ
7
σ
7
σ
8
σ
5
σ
6
σ
2
σ
1
σ
4
σ
3
σ
3
σ
4
σ
1
σ
2
a
7
σ
7
σ
8
σ
5
σ
6
σ
66
σ
5
σ
8
σ
7
σ
3
σ
4
σ
1
σ
2
σ
2
σ
1
σ
4
σ
3
σ
4
σ
3
σ
2
σ
1
σ
1
σ
2
σ
3
σ
4
a
8
σ
8
σ
7
σ
6
σ
5
σ
5
σ
6
σ
7
σ
8
σ
8
σ
7
σ
66
σ
5
σ
5
σ
6
σ
7
σ
8
σ
4
σ
3
σ
2
σ
1
σ
1
σ
2
σ
3
σ
4
σ
3
σ
4
σ
1
σ
2
σ
2
σ
1
σ
4
σ
3
σ
7
σ
8
σ
5
σ
6
σ
6
σ
5
σ
8
σ
7
σ
2
σ
1
σ
4
σ
3
σ
3
σ
4
σ
1
σ
2
σ
6
σ
5
σ
8
σ
7
σ
7
σ
8
σ
5
σ
6
σ
5
σ
6
σ
7
σ
8
σ
8
σ
7
σ
6
σ
5
σ
1
σ
2
σ
3
σ
4
σ
4
σ
3
σ
2
σ
1
Рис. 3.68
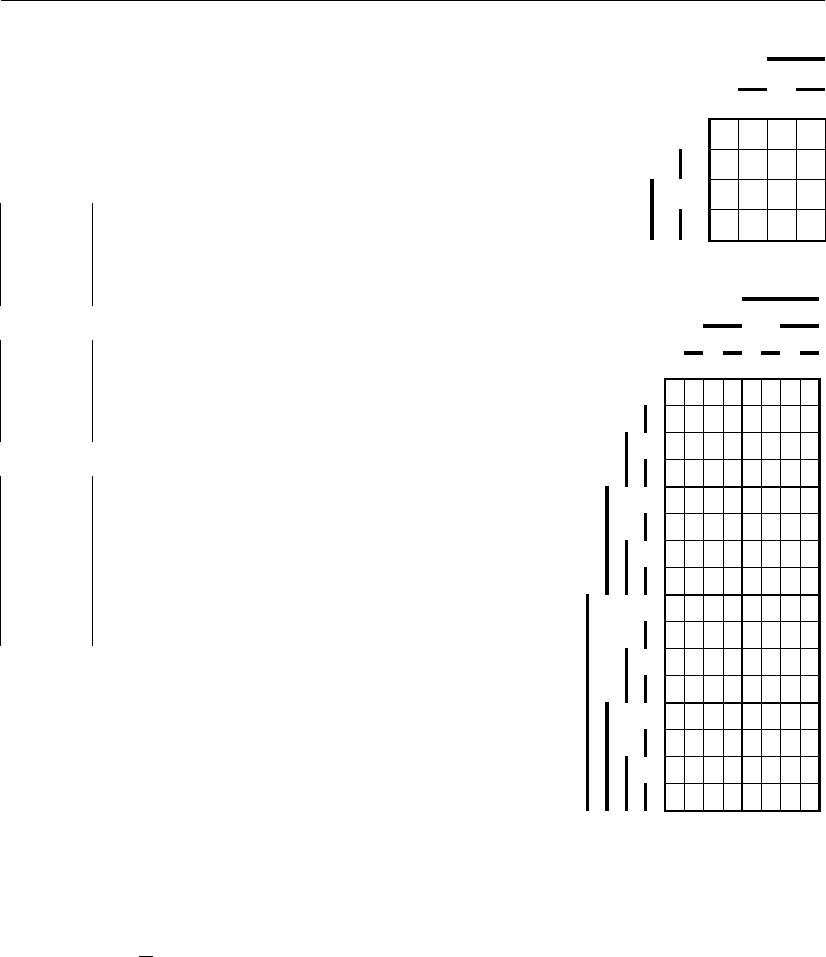
Контролеспособность позиционных систем счисления
193
Заполнение остальных больших ячеек информа-
ционного цифрового пространства, которые имеют
такие же координаты, как s
1
, подчиняется следую-
щим взаимным перестановкам эквивалентных цифр
контрольной части кода:
На основании зависимостей рис. 3.69, выполняя
определенные преобразования, аналогичные тем,
которые проводились выше, можно получить гра-
фические образы логических функций, связывающие
между собой контрольные и информационные сиг-
налы разрядов.
На рис. 3.70 приведена такая зависимость между
сигналом контрольного разряда x
1
и информацион-
ными разрядами x
1
= F(a
1
, a
2
, a
4
, a
5
, a
7
, a
9
, a
11
), которая полностью определяется
выражением λ
7
(0).
Аналогичные зависимости представляются для сигналов других контроль-
ных разрядов, которые отличаются иными группами сигналов информацион-
ных разрядов, а именно:
a
5
a
4
s
1
s
2
s
3
s
4
a
10
s
4
s
3
s
2
s
1
a
11
s
1
s
2
s
3
s
4
s
4
s
3
s
2
s
1
а)
a
3
a
2
S
1
a
1
a
6
0 3 5 6 6 5 3 0
a
7
10 9 15 12 12 15 9 10
11 8 14 13 13 14 8 11
a
8
1 2 4 7 7 4 2 1
12 15 9 10 10 9 15 12
6 5 3 0 0 3 5 6
7 4 2 1 1 2 4 7
a
9
13 14 8 11 11 8 14 13
13 14 8 11 11 8 14 13
7 4 2 1 1 2 4 7
6 5 3 0 0 3 5 6
12 15 9 10 10 9 15 12
1 2 4 7 7 4 2 1
11 8 14 13 13 14 8 11
10 9 15 12 12 15 9 10
0 3 5 6 6 5 3 0
б)
Рис. 3.69
s
1
⇔
s
2
0 1 2 3 8 9 10 11
≡
¤ ¤
¤ ¤ ¤ ¤ ¤ ¤
s
3
⇔
s
4
7 6 5 4 15 14 13 12,
s
1
⇔
s
4
0 1 2 3 4 5 6 7
≡
¤
¤ ¤ ¤ ¤ ¤ ¤ ¤
s
2
⇔
s
3
14 15 12 13 10 11 8 9,
s
1
⇔
s
1
s
2
⇔
s
2
0 1 2 3 4 5 6 7
≡
¤
¤ ¤ ¤ ¤ ¤ ¤ ¤
s
3
⇔
s
3
15 14 13 12 11 10 9 8.
s
4
⇔
s
4
x
2
= F(a
1
, a
2
, a
3
, a
4
, a
5
);
x
3
= F(a
2
, a
3
, a
4
, a
8
, a
9
);
x
4
= F(a
5
, a
6
, a
7
, a
8
, a
9
, a
10
, a
11
).
Глава 3
194
В представленных нами при-
мерах синтеза полностью контро-
леспособных кодов относительно
одиночных ошибок, тем более ох-
ватывающих все их классы, долж-
ны содержаться все коды, синте-
зированные каким-либо иным
способом. Например, замечатель-
ная процедура синтеза контроле-
способных кодов Хемминга для
исправления одиночных ошибок
представлена на рис. 3.66 в пер-
вом классе и отмечена звездочкой,
а только что синтезированный код
основания n = 2
11
также является
кодом Хемминга.
Связь между контрольными k и
информационными i сигналами раз-
рядов полностью контролеспособ-
ных кодов определяется зависимо-
стью i = [2
k
– (k+1)], что для осно-
ваний n = 2
1
, 2
4
, 2
11
, 2
26
, .... позволя-
ет исправлять все одиночные ошиб-
ки.
Отмеченное здесь не означает,
что для этих оснований и любых
других нет возможности обнаружения и исправления большего количества
комбинаций ошибок, чем рассмотрено выше. Увеличение числа контроль-
ных разрядов сверх представленного приведет к тому, что при геометриче-
ском способе синтеза кодов необходимо будет в ячейках пространства рис.
3.53 размещать, например, фигуры основания n = 2, позволяющие исправ-
лять одиночные, двойные и т.д. ошибки, частично рассмотренные в п. 3.1.
Именно эти достаточно сложные задачи будут детально рассмотрены в
последующих главах книги, а представленный в этом параграфе синтез со-
вершенных кодов и определение числа этих кодов носят предварительный,
вводный характер и будут уточнены в дальнейшем изложении.
a
4
a
2
x
1
a
1
a
5
a
7
a
9
a
11
Рис. 3.70

Контролеспособность позиционных систем счисления
195
3.8. Решение задачи повышения надежности логических и
цифровых устройств в режиме реального времени
Известно, что надежность логических и цифровых устройств можно по-
высить, не используя резервирования их элементов. Для достижения этой цели
необходимо применять высоконадежные элементы и схемы с большим запа-
сом надежности, где уделяется повышенное внимание технологии их изготов-
ления и сборки. Однако этот правильный путь не может обеспечить надежные
вычислительные системы многолетней длительной эксплуатации без челове-
ческого сопровождения и хранения, используемые для проведения, например,
исследований космического пространства и управления ответственными бор-
товыми системами реального масштаба времени [13].
С целью повышения надежности таких систем нередко используется их
резервирование со схемой голосования. Такой путь повышения надежности
был предложен Дж. фон Нейманом [14], который разработал и проанализиро-
вал схему тройного резервирования элементов с мажоритарной функцией го-
лосования. Геометрический вариант подобного подхода к проблеме исправле-
ния ошибок был представлен нами в предыдущих разделах. Этот подход за-
ключается в исправлении всех ошибок конечной двоичной системы счисле-
ния, например, всех одиночных ошибок или одновременно всех одиночных и
двойных ошибок; одновременно всех одиночных, двойных и тройных ошибок
и т.д. Под термином «всех» понимается, что конкретная ошибка может суще-
ствовать все время, и она должна при этом непременно исправляться. Следо-
вательно, исправление ошибок и резервирование, например, элементов циф-
ровой системы здесь будут совпадать при условии, что исправление ошибок
каждого разряда систематического кода осуществляется отдельной схемой, не
имеющей общих элементов со схемами исправления ошибок других разрядов.
Повышение надежности с мажоритарной функцией голосования
Дж. фон Неймана, где равные одновременные сигналы F(a) одинаковых эле-
ментов 1 (рис. 3.71) объединяются мажоритарной схемой голосования 2, име-
ет много общего с задачей исправления всех одиночных ошибок в системе
счисления основания два (см. рис. 3.3).
В самом деле, исправление всех одиноч-
ных ошибок в каждом из разрядов любой
системы счисления является резервировани-
ем канала связи, что равноценно резервиро-
ванию выходных сигналов F(a) рис. 3.71.
Здесь следует учитывать, что при несо-
вершенстве мажоритарной схемы вероят-
ность безотказной работы резервированной
схемы определяется [15] зависимостью
P
p
= P
2
(3 – 2P)P
m
,
A F(a)
1
A F(a) F(a)
1
A F(a)
1
2
Рис. 3.71

Глава 3
196
где
P – вероятность безотказной работы отдельной нерезервированной схе-
мы;
P
m
– вероятность безотказной работы отдельной мажоритарной схемы.
Из анализа этого выражения следует, что в резервированной таким образом
схеме вероятность безотказной работы выше, чем в нерезервированной, но до оп-
ределенного момента времени, после которого она становится меньше нерезерви-
рованной схемы. Поэтому средняя наработка на отказ становится недостаточной
для работы в течение требуемого интервала времени и для получения необходи-
мого значения средней наработки на отказ вся схема должна будет строиться с
многократным мажоритарным резервированием (см. рис. 3.5, рис. 3.6) либо необ-
ходимо будет выполнить резервирование мажоритарного элемента.
Построение логических и цифровых устройств, в систематических кодах с
исправлением всех заданных заранее ошибок, вполне реально, но требует зна-
чительных аппаратурных затрат. При этом наиболее целесообразно использо-
вать систематические коды с большей разрядностью его информационной час-
ти, что позволяет уменьшать аппаратурные затраты.
Правильность этого заключения легко показать на примере выполнения
комбинационных схем бинарных логических функций при исправлении всех
одиночных ошибок двоичной системы счисления, где систематический код
первого операнда будет содержать один информационный разряд – a
1
и два
контрольных разряда – x
1
, x
2
. Для второго операнда это будут соответственно
разряды b
1
, z
1
, z
2
.
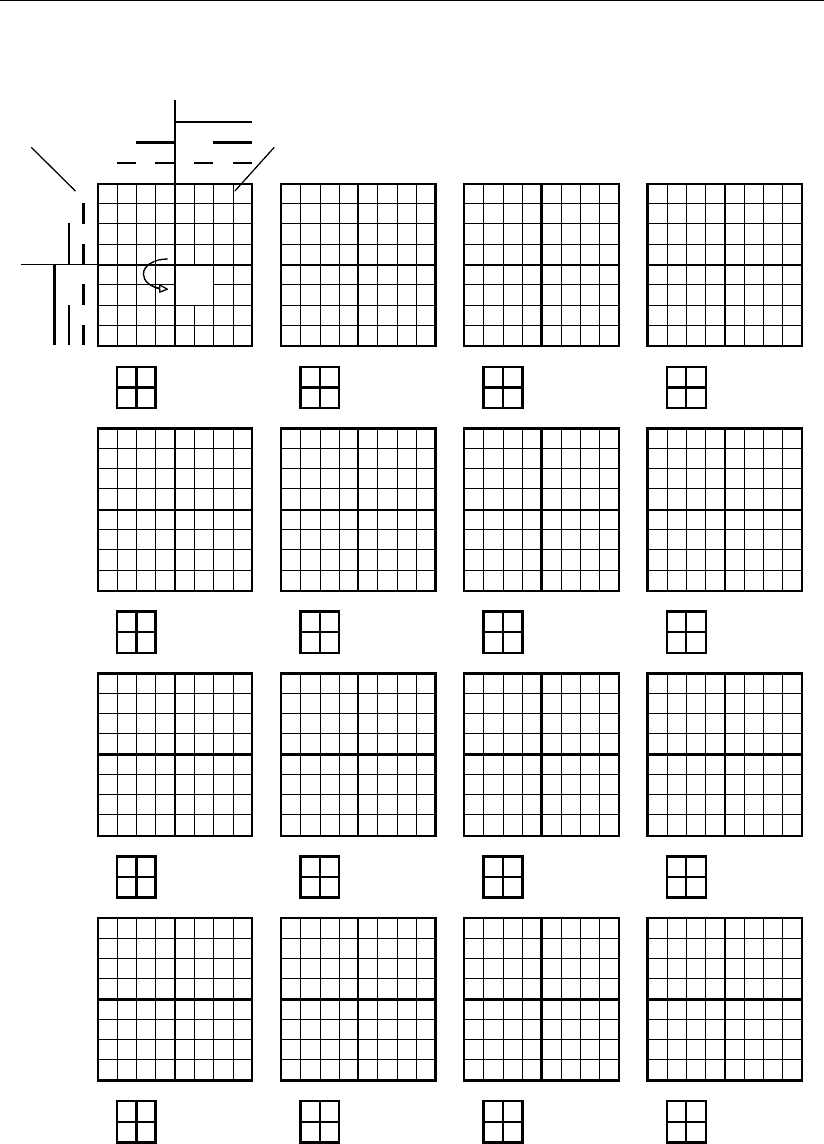
Геометрические образы бинарных логических функций y
1
– y
16
с исправ-
лением одиночных ошибок и аналогичные им функции без исправления оши-
бок приведены на рис. 3.72 в многомерном цифровом пространстве координат
a
1
, x
1
, x
2
;
b
1
, z
1
, z
2
. Звездочками в ячейках этого пространства представляются
геометрические образы выходных функций, где цветом выделены безошибоч-
ные значения входных сигналов.
Все мысленные повороты относительно осей симметрии 1–5 этого про-
странства, сопровождаемые соответствующим изменением входных сигналов
координат, переводят геометрические образы этих функций в новые положе-
ния так же, как это имеет место в двоичном коде без исправления ошибок. По-
этому в каждой из групп одинаковых геометрических образов (y
7
, y
10
; y
2
, y
3
, y
9
,
y
5
; y
15
, y
14
, y
12
, y
8
; y
4
, y
11
, y
13
, y
6
) можно представить только одну, а остальные
будут определяться соответствующими поворотами относительно осей сим-
метрии этого цифрового пространства.
Пусть это будут функции y
7
, y
2
, y
15
, y
4
, а также функция универсального
цифрового пространства – y
16
, геометрический образ которой при всех мыс-
ленных поворотах относительно осей симметрии цифрового пространства так
же, как и прежде, не меняет своего положения в координатах этого простран-
ства.
Контролеспособность позиционных систем счисления
197
1
a
3
x
2
4
x
1
b
* ******* ******* *
z
1
** **
** **
z
2
*** *
** **
2
5
*** *
*** *
* ********** * * ***
** * *
y
1
**
y
16
*
y
7
*
y
10
* ** * * ***
**
**
**
**
**
**
******* *
**
y
2
y
3
*
y
9
*
y
5
******* * * ***************
** * ** *
** * ** *
***** *
** * ** *
***** *
***** *
* ****************** * * ***
** ****
**
y
15
**
y
14
*
y
8
*
y
12
* ******* ******* *
** * *
** * *
** **
** * *
** **
** **
*************** *
** * *
y
4
*
y
11
**
y
13
*
y
6
Рис. 3.72
Глава 3
198
y
7
=
x
1
x
2
b
1
z
1
z
2
∨ x
1
a
1
b
1
z
1
z
2
∨ x
2
a
1
b
1
z
1
z
2
∨
∨ z
1
z
2
a
1
x
1
x
2
∨ z
1
b
2
a
1
x
1
x
2
∨ z
2
b
2
a
1
x
1
x
2
∨
∨ z
1
z
2
a
1
x
1
x
2
∨ z
1
b
2
a
1
x
1
x
2
∨ z
2
b
2
a
1
x
1
x
2
∨
∨ x
1
x
2
b
1
z
1
z
2
∨ x
1
a
1
b
1
z
1
z
2
∨
x
2
a
1
b
1
z
1
z
2
;
y
2
=
x
1
x
2
b
1
z
1
z
2
∨ x
2
a
1
b
1
z
1
z
2
∨ x
1
a
1
b
1
z
1
z
2
∨
∨ z
1
z
2
a
1
x
1
x
2
∨ z
2
b
1
a
1
x
1
x
2
∨
z
1
b
1
a
1
x
1
x
2
;
y
15
=
x
1
x
2
a
1
∨ z
1
z
2
b
1
;
y
4
=
z
1
z
2
a
1
x
1
x
2
∨
z
2
b
2
a
1
x
1
x
2
∨
z
1
b
2
a
1
x
1
x
2
∨
∨ z
1
z
2
a
1
x
1
x
2
∨
z
2
b
2
a
1
x
1
x
2
∨
z
1
b
2
a
1
x
1
x
2
∨
∨ z
1
z
2
b
1
;
Y
16
=
x
1
x
2
a
1
∨ x
1
x
2
a
1
∨ z
1
z
2
b
1
∨ z
1
z
2
b
1
.
Нерациональное использование многомерного цифрового пространства,
где универсальное пространство использует только его «оболочку», и слож-
ность при этом логических выражений даже для простых бинарных функций
свидетельствуют о неперспективности использования этого кода для синтеза
логических и цифровых устройств еще больших оснований систем счисления.
Следовательно, необходимо использовать систематические коды с боль-
шой разрядностью информационной части, где общее число разрядов систе-
матического кода определяется выражением
(i + k) = (2
k – 1
),
где
i – число информационных разрядов кода;
k – число контрольных разрядов кода.
Уже для k = 9 число информационных разрядов настолько большое, что
емкость такого многомерного цифрового пространства, которое является кон-
тролеспособным относительно одиночных ошибок, превосходит единицу из-
мерения Гугол (10
100
), название которой предложил американский математик
Кастнер. Хотя натуральный ряд чисел и бесконечен, Гугол – это граница ис-
числяемого мира. Обратимся к просторам космоса и выразим расстояние меж-
ду звездами в ангстремах, который равен одной десятимиллионной части
миллиметра. Тогда световой год, который определяет расстояние, проходимое
солнечным лучом в течение года, представляется только числом 10
26
Å. Даже
расстояние до самых удаленных галактик не превышает 6×10
27
Å. Возраст
Вселенной, выраженный в световых годах, составляет менее 10
40
Å. Примерно
столько же составляет вся энергия, излучаемая всеми звездами Вселенной, вы-
раженная в микроваттах. Поэтому в практической деятельности мы всегда
встречаемся только с конечными логическими и цифровыми устройствами,
что позволяет говорить о конечности исследуемого нами цифрового про-
странства, где содержимое каждой его ячейки может контролироваться, т.е.
исправляться при соответствующем соотношении информационных и кон-
трольных частей систематического кода.
Контролеспособность позиционных систем счисления
199
Перед тем как приступить к применению синтезированных нами геомет-
рическим способом систематических кодов, предназначенных для исправле-
ния, например, всех одиночных ошибок, в решении задач резервирования ло-
гических и цифровых устройств без памяти (комбинационные схемы) и с па-
мятью (автоматы), необходимо еще раз уточнить связь расширенного нату-
рального ряда чисел с логическими и цифровыми функциями и схемами, их
реализующими.
Входным аргументом любой логической функции и сигналом схемы, ее
реализующей, является натуральное число, которое определяет номер ячейки
цифрового пространства, где для выходной двухзначной функции записыва-
ются логический нуль или единица, которые также соответствуют натураль-
ному числу. Входное натуральное число поступает на входные шины схемы в
основном двоичном эквиваленте в одном из значений числа от 0 до (2
n
– 1).
N (a
1
,…, a
n
) N
1
(a
1
,…, a
i
) N
2
(a
i+1
,…, a
n
) N
1
(a
1
) N
2
(a
2
) N
3
(a
3
) N
n
(a
n
)
…
F(N) F(N)
…
F(N)
N (c
1
) N (c
1
) N (c
1
)
а)
б)
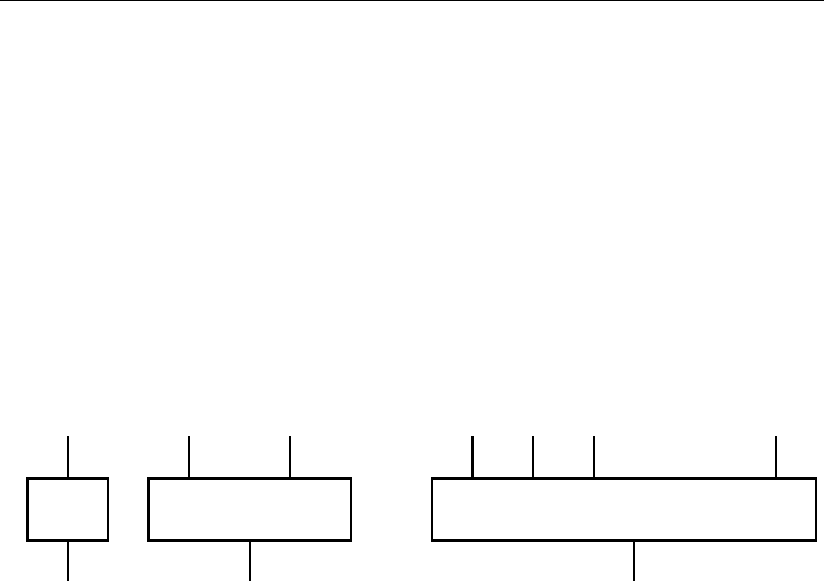
Рис. 3.73
в)
При этом натуральное входное число может представляться, как однораз-
рядным (рис. 3.73, а) в одномерном цифровом пространстве, двухразрядным
(см. рис. 3.73, б) в двухмерном пространстве и т.д. вплоть до максимальной
разрядности (см. рис. 3.73, в) n-мерного пространства.
Если выходная функция многозначная, а такой может быть представлена
любая выходная многоразрядная функция двоичного кода, то в ячейки много-
мерного цифрового пространства, номер которых определяется натуральным
входным числом, записывается также натуральное число, определяемое этой
значностью. Например, для четырехзначной выходной логической функции –
это двоичное число от 0 до 3, для восьмизначной – двоичное число от 0 до 7
и т.д. Здесь разрядность выходной функции может быть равной или различной
входной, при этом совпадать или различаться с ней по числу разрядов, а также
неограниченно превосходить ее по числу разрядов.
Все комбинационные схемы машинной арифметики, которые используют
при кодировании цифр разрядов основной двоичный код, являются также ло-
гическими схемами, где логическая связь между натуральным входным чис-
лом или цифрой в пределах одного разряда и выходным натуральным опреде-
ляется законами арифметики.
В машинной арифметике, где при кодировании цифр разрядов используется
неосновной двоичный код, т.е. «весовые» значения цифр этого кода не совпадают
с «весовыми» значениями основного двоичного кода, эквивалентность логических
