Киселева М.В. Информатика
Подождите немного. Документ загружается.

21
Пример 5. При Р=2, n=10 и m=6 диапазон чисел простирается примерно от 10
-19
до
10
19
. (Сравните примером 2.3).
Системы счисления, используемые при работе с ЭВМ.
В ВТ применяют позиционные СС с недесятичным основанием: двоичную,
восьмеричную, шестнадцатеричную и др. Для обозначения используемой СС числа
заключают в скобки и индексом указывают основание СС:
.)91(,)735(,)1011(,)15(
168210
FEA
Иногда скобки опускают и оставляют только индекс:
.91,735,1011,15
168210
FEA
Есть еще один способ обозначения СС: при помощи латинских букв добавляемых
после числа. Например,
15D; 1011 В; 735Q; 1EA9FH.
Двоичная система счисления.
Основание Р=2. Алфавит включает две двоичные цифры: 0, 1. Любое число
C= C
n
C
n-1
…C
1
C
0
C
-1
C
-m
есть сумма степеней числа Р=2,
C= C
n
⋅ 2
n
+C
n-1
⋅ 2
n-1
+…+C
1
⋅ 2
1
+C
0
⋅
2
0
+C
-1
⋅ 2
-1
+…+C
-m
⋅ 2
-m
(1.1)
Пример 6. 101011,11
2
=1⋅2
5
+ 0⋅2
4
+ 1⋅2
3
+ 0⋅2
2
+1⋅2
1
+ 1⋅2
0
+1⋅2
-1
+ 1⋅2
-2
=
= 32+8+2+1+0,5+0,25=43,75
10
.
Веса разрядов в двоичной системе счисления равны 1, 4, 8,16,... влево от запятой и
0,5; 0,25; 0,125; 0,625;... вправо от запятой.
Шестнадцатеричная и восьмеричная СС используются при составлении программ на
языке машинных кодов для более короткой и удобной записи двоичных кодов — команд,
данных, адресов и операндов.
Для изображения цифр, больших 9, в шестнадцатеричной системе счисления
применяются латинские буквы A, B, C, D, E, F. Изображения первых шестнадцати чисел в
десятичной, двоичной и шестнадцатеричной системах счисления приведены в таблице 1.
Двоично-десятичная система счисления получила большое распространение в
современных ЭВМ ввиду легкости перевода в десятичную систему и обратно. Она
используется там, где основное внимание уделяется не простоте технического построения
машины, а удобству работы пользователя. В этой системе счисления все десятичные
цифры отдельно кодируются четырьмя двоичными цифрами.
Пример 7. Десятичное число 9703 в двоично-десятичной системе выглядит так:
1001 0111 0000 0011.
Таблица 1
Системы счисления
Десятичная Двоичная Восьмеричная Шестнадцатеричная
о о 0 о
1 1 1 1
2 10 2 2
3 11 3 3
4 100 4 4
5 101 5 5
6 110 6 6
7 111 7 7
8 1000 10 8
9 1001 11 9
10 1010 12 А

22
11 1011 13 В
12 1100 14 C
13 1101 15 D
14 1110 16 Е
15 1111 17 F
16 10000 20 10
17 10001 21 11
Двоичная арифметика
Преимущество двоичной системы счисления над десятичной с точки зрения ЦВМ
состоит в следующем:
- требуются элементы с двумя устойчивыми состояниями;
- существенно упрощаются арифметические операции;
- оборудования требуется в 1,5 раза меньше;
- позволяет применить аппарат математической логики для анализа и синтеза схем.
Недостатки двоичной системы счисления состоят в следующем:
- большая длина записи
чисел;
- при вводе и выводе информации требуется перевод в десятичную систему
счисления.
Рассмотрим, как выполняются основные действия в двоичной арифметике.
Сложение
Вычитание Умножение Деление
0+0=0 0-0=0 0х0=0 0:1=0
0+1=1 1-0=1 0х1=0 1:1=1
1+0=1 1-1=0 1х0=0
1+1=10 10-1=1 1х1=1
Правила арифметики во всех позиционных системах счисления одинаковы, т.е.
сложение, умножение и вычитание начинают с младших разрядов, деление - со старших.
При сложении единица переноса складывается с цифрами соседнего старшего
разряда. При вычитании единица заёма старшего разряда дает две единицы в младшем
соседнем разряде.
Пример 8.
Умножение двоичных чисел аналогично умножению десятичных, но т.к. умножаем
только на 0 и 1, то умножение сводится к операции сдвига и сложения. Положение точки,
отделяющей целую часть от дробной части, определяется так же, как и при умножении
десятичных чисел.
Пример 9.
1011,1
х 101,01
10111
10111 - сдвинутое на 2 разряда влево множимое
10111
- сдвинутое на 4 разряда влево множимое
111100,011
1) 110111,01 55,25 2) 11011,10 27,5
+ 10011,10
+19,5 - 1101,01 -13,25
1001010,11 74,75 1110,01 14,25
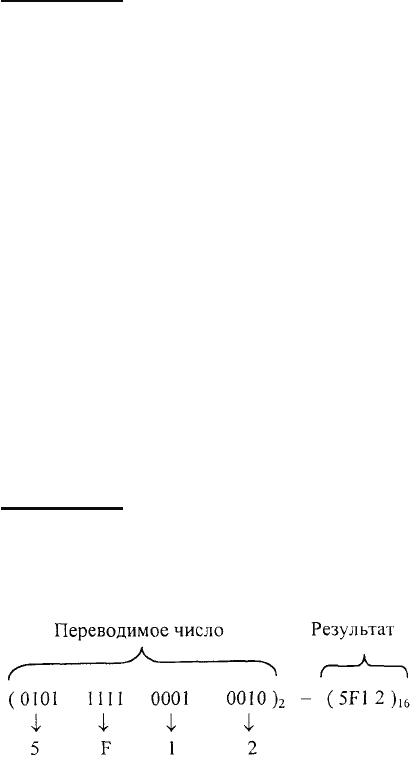
23
Перевод чисел из одной системы счисления в другую
Задача перевода из одной системы счисления в другую часто встречается при
программировании и особенно часто — при программировании на языке Ассемблера.
Например, при определении адреса ячейки памяти, для получения двоичного или
шестнадцатеричного эквивалента десятичного числа. Отдельные стандартные процедуры
языков программирования Паскаль, Бейсик, HTML и Си требуют задания параметров в
шестнадцатеричной СС. Отыскать неисправность
в ЭВМ практически невозможно без
представлений о двоичной СС.
Сначала рассмотрим перевод из двоичной системы счисления в шестнадцатеричную
и наоборот. Это наиболее просто в связи с тем, что 16=2
4
.
Правило 1. Для перевода шестнадцатеричного числа в двоичное надо каждую
цифру заменить четырехразрядным двоичным числом. Незначащие нули отбросить.
Пример 10.
305,4
16
=0011 0000 0101,0100
2
=1100000101,01
2
Ещё пример: Перевести число 7D2.ЕН из шестнадцатеричной СС в двоичную СС.
Решение
Переводимое число Результат
↑↑
=
↓↓↓↓
216
)111.01111101001()
11100010
.2
11010111
7( ED
РезультатчислоеПереводимо
4443444214444434444421
Отмеченные крайние нули следует отбросить.
Правило 2. Для перевода числа из двоичной системы счисления в
шестнадцатеричную надо число разбить на четверки влево и вправо от запятой. Крайние
группы, если необходимо дополнить нулями. Затем каждую четверку двоичных цифр
заменить соответствующей шестнадцатеричной цифрой.
Пример 11.
1010111,1101101
2
=0101 0111,1101 1010
2
=57,DA
16
Ещё пример: перевести число 10111110001.001В из двоичной СС в
шестнадцатеричную СС.
Решение.
Рассмотрим общие правила перевода чисел из одной системы счисления в другую.
Эти правила зависят от того, в какой системе счисления осуществляются арифметические
операции, связанные с преобразованием чисел, - в той, в какой представлено исходное
число, или в той, в которую оно переводится.
Правило 3.
Задано число С, представленное в системе счисления с основанием S:
C = C
n
C
n-1
…C
1
C
0
C
-1
C
-m
Нужно перевести его в h-систему, выполняя действия в новой системе счисления (в
h-системе).
24
Для этого нужно представить его в виде суммы степеней S :
C= C
n
S
n
+C
n-1
S
n-1
+…+C
1
S
1
+C
0
S
0
+C
-1
S
-1
+…+C
-m
S
-m
,
где основание S, коэффициенты c и номера разрядов i выражены в новой h-системе.
Все действия надо выполнять в h-системе.
Пример 12.
1) Перевести 2Е5,А
16
в десятичную систему счисления:
2Е5,А
16
=2⋅ 16
2
+14⋅16
1
+5⋅16
0
+10⋅16
-1
=741,625
10
2) Перевести 52
10
в двоичную систему счисления:
52
10
=101⋅1010
1
+10⋅1010
0
=110010+10=110100
2
3) Перевести 1101,101 в десятичную систему счисления:
1101,101
2
= 1⋅ 2
3
+1⋅ 2
2
+0⋅ 2
1
+1⋅ 2
0
+1⋅ 2
-1
+0⋅ 2
-2
+1⋅ 2
-3
=13,625
10
Этот способ удобен при S<h и особенно для ручного перевода в десятичную систему
счисления.
Рассмотрим перевод целого числа С (2.2) из S-системы в h-систему в арифметике S-
системы счисления.
Правило 4. Для перевода целого числа из S-системы в h-систему счисления в
арифметике S-системы нужно последовательно делить это число и получающиеся частные
на h до тех пор, пока частное не станет меньше h. Старшей цифрой в новой записи числа
будет последнее частное, а следующие за ней цифры дают остатки, вписанные в
последовательности, обратной их
получению. Все вычисления производятся в старой S-
системе. (При S<h прежде, чем записать число, надо получившиеся остатки переписать
в цифры h-системы).
Пример 13.
1) Перевести число 70 в двоичную систему счисления.
При переводе наиболее частой ошибкой является неверная запись результата. Запись
двоичного числа следует начинать со старшего значащего разряда (СЗР), а заканчивать
записью младшего значащего разряда (МЗР). Следует помнить, что при делении первым
получается значение МЗР.
В ЭВМ с целью упрощения арифметических операций
применяют специальные
коды для представления чисел. При помощи этих кодов:
• автоматически определяется знак результата;
• операция вычитания сводится к арифметическому сложению кодов чисел;
• упрощается операционная часть ЭВМ.
70
⏐
2
0 35 ⏐2
1 17 ⏐2
1 8 ⏐2
0 4 ⏐2
0 2 ⏐2 70
10
=1000110
2
0 1
2) Перевести 10000000 в десятичную систему
счисления
10000000
⏐1010
- 1010
1100 ⏐1010
1100 - 1010
1
- 1010
10=2
10
1000=8
10
10000000
2
=128
1
0

25
Прямой , обратный и дополнительный коды чисел
В ЭВМ используется прямой, обратный и дополнительный коды чисел. Знак “+”
кодируется нулем (0), “-” - единицей (1), которые записываются в дополнительном
старшем разряде - знаковом разряде.
1. Прямой двоичный код Рпр(х) — это такое представление двоичного числа х, при
котором знак «плюс» кодируется нулем в старшем разряде числа, а знак «минус» —
единицей. При этом старший разряд называется
знаковым.
Сложение в прямом коде не вызывает затруднений, когда у слагаемых одинаковые
знаки: сложить модули и сумме присвоить знак слагаемых. При вычитании чисел в
прямом коде нужно сначала определить больший модуль, от него отнять меньший и
результату присвоить знак большего модуля.
2. Обратный код Робр(х) получается из прямого кода по следующему правилу:
⎪
⎩
⎪
⎨
⎧
≤
≥
=
0)(1
0)(0
)(
'
'
xприxP
xприxP
xP
пр
пр
обр
Из приведенного выражения видно, что
обратный код для положительных чисел
совпадает с прямым кодом. Чтобы представить отрицательное двоичное число в
обратном коде нужно оставить в знаковом разряде 1, во всех значащих разрядах
заменить 1 на 0, а 0 на 1. Такая операция называется инвертированием и обозначается
горизонтальной чертой над инвертируемым выражением.
3. Дополнительный код Рдоп(х) образуется следующим образом:
⎪
⎩
⎪
⎨
⎧
≤+
≥
=
01)(1
0)(0
)(
'
'
xприxP
xприxP
xP
пр
пр
доп
Из выражения видно, что дополнительный код положительного числа совпадает с
прямым кодом, а для отрицательного числа получается инверсией всех значащих
разрядов и добавлением единицы к младшему разряду результата.
Дополнительный код может быть получен из обратного кода путём прибавления 1
к младшему разряду обратного кода (естественно, с учётом переносов между
разрядами).
Итак:
Положительные числа в прямом, обратном и дополнительном кодах изображаются
одинаково - двоичными кодами с цифрой 0 в знаковом разряде.
Отрицательные числа в прямом, обратном и дополнительном кодах имеют разное
изображение.
Обычно
отрицательные десятичные числа при вводе в машину автоматически
преобразуются в обратный или дополнительный двоичный код и в таком виде
хранятся, перемещаются и участвуют в операциях. При выводе таких чисел из машины
происходит
обратное преобразование в отрицательные десятичные числа.
Пример 14: Получить обратный код для числа х=-13D.
Решение.
кодьныйдополнителxР
кодобратныйxP
кодпрямойxP
доп
обр
пр
−=
−=
−=
2
2
2
)0011'1()(
)0010'1()(
)1101'1()(

26
Нетрудно доказать, что (по модулю):
• Обратный код от обратного кода дает прямой код числа.
• Дополнительный код от дополнительного кода дает прямой код числа.
Сложение чисел в прямом и дополнительном коде
Можно строго математически доказать следующие правила.
Правило 1. При сложении дополнительных кодов чисел знаковые разряды
складываются аналогично остальным, перенос из знакового разряда теряется, результат
получается в дополнительном коде.
Правило 2. При сложении чисел в обратном коде знаковые разряды складываются
аналогично остальным, перенос из знакового разряда прибавляется к младшему разряду
результата (так называемый циклический перенос), результат получается в обратном коде.
Таким образом, применение обратного и дополнительного кода упрощает
алгебраическое сложение. Сложение чисел с разными знаками заменяется сложением их
соответствующих кодов, знак при этом получается автоматически.
Пример 14.
Пример 15. Выполнить алгебраическое сложение с использованием
дополнительного кода для чисел
X1 = 7D и X2 = -3D.
Решение.
Необходимо найти сумму: у = X1 +X2.
Учитывая, что
X1 > 0, это число нужно представить в прямом коде, а так как X2< 0,
то X
2 нужно перевести в дополнительный код.
Так как результат положителен (в знаковом разряде
Р(у) - 0), значит, он представлен в
прямом коде. После перевода двоичного числа в десятичную СС получим ответ:
у = +4D.
Пример 16. Выполнить алгебраическое сложение с использованием дополнительного
кода для чисел
X1= 8D и X2 = -13D.
Необходимо найти сумму: у = X1 +X2.
Число
X1 нужно представить в прямом коде, а X2 — в дополнительном коде.
1) X=0,0101, Y=-0,0011
X
доп
=0,0101, Y
доп
=1,1101
X
доп
+ Y
доп
= 0,0101
+1,1101
1
0 0010
(
3) A=+0,10111, B=-0,01010
A
обр
=0,10111, B
обр
=1,10101
A
обр
+ B
обр
= 0,10111
+1,10101
10,01100
1
(циклический
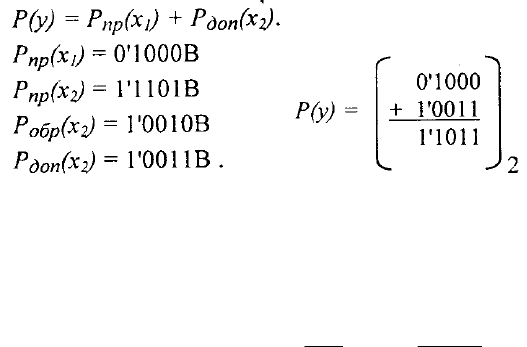
27
В знаковом разряде стоит единица и, значит, результат получен в дополнительном коде.
Для перехода от дополнительного кода
Рдоп(y)=1'1011B
к прямому коду
Рпр(у) необходимо выполнить следующие преобразования:
Робр(у) = Рдоп(у) - 1 = 1'1011B - 1 = 1'1010B,
Рпр(у) =
BByP
обр
0101'11010'1)( ==
Переходя от двоичной СС к десятичной СС, получим ответ:
y=-5D.

28
Варианты представления информации в ПК
Как уже упоминалось, вся информация (данные) представлена в виде двоичных
кодов. Для удобства работы введены следующие термины, обозначающие совокупности
двоичных разрядов (табл.2.2). Эти единицы обычно используются в качестве единиц
измерения объемов информации, хранимой или обрабатываемой в ЭВМ.
Таблица 2.2. Двоичные совокупности
Количество
двоичных
разрядов в
группе
1
8
16
8*1024
8*1024
2
8*1024
3
8*1024
4
Наименован
ие единицы
измерения
Б
и
т
Б
а
й
т
Пара-
граф
Килобайт
(Кбайт)
Мегабайт
(Мбайт)
Гигабайт
(Гбайт)
Терабайт
(Тбайт)
Восемь последовательных битов составляют
байт. Как правило, код символа
хранится в одном байте. Такие кодировки называются
однобайтными. В одном байте
можно закодировать значение одного символа из 256 возможных (2
8
=256). Примером
такой кодировки может служить код ASCII (American Code for Information Interchange –
американский код обмена информацией). В настоящее время все большее применение
приобретает двухбайтная кодировка Unicode, в ней коды символов могут иметь значение
от 0 до 65535. В этой кодировке имеются коды для практически всех применяемых
символов (букв алфавитов разных языков, математических , декоративных символов и
т.д.)
Последовательность нескольких
битов или байтов часто называют полем данных.
Биты в числе (в слове, в поле и т.п.) нумеруются справа налево, начиная с 0-го разряда.
В ПК могут обрабатываться поля постоянной и переменной длины.
Поля постоянной длины:
• слово – 2 байта;
• полуслово – 1 байт;
• двойное слово – 4байта;
• расширенное слово –8байт.
Числа с фиксированной запятой чаще всего имеют формат слова и полуслова,
числа с плавающей точкой – формат двойного и расширенного слова.
Поля переменной длины могут иметь любой размер от 0 до 256 байт, но
обязательно равный целому числу байтов.
Пример 2.15.
Структурно запись числа –193
10
=-11000001
2
в разрядной сетке ПК выглядит
следующим образом.
Число с фиксированной запятой формата слово со знаком.
Знак Абсолютная величина числа
N раз-
ряда
15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0
Число
1 0 0 0 0 0 0 0 1 1 0 0 0 0 0 1
29
Информационно-логические основы построения ЭВМ
Основы алгебры логики
Для описания логики функционирования аппаратных и программных средств ЭВМ
используется алгебра
логики или, как ее часто называют, булева алгебра.
Основоположником этого раздела математики был Дж.Буль.
Булева алгебра оперирует с логическими переменными, которые могут принимать
только два значения:
истина или ложь, обозначаемые соответственно 1 и 0.
Как ранее отмечалось, основной системой счисления ЭВМ является двоичная СС, в
которой также используются только две цифры: 1 и 0. Таким образом, одни и те же
цифровые устройства ЭВМ могут применяться для обработки как числовой информации в
двоичной СС, так и логических переменных. Это обуславливает универсальность
(однотипность) схемной реализации
процесса обработки информации в ЭВМ.
Алгебра логики – это раздел математической логики, значения всех элементов
которой определены в двухэлементном множестве: 0 или 1. Алгебра логики оперирует с
логическими высказываниями.
Высказывание – это любое предложение, в отношении которого имеет смысл
утверждение о его истинности или ложности. При этом считается, что высказывание
удовлетворяет закону исключённого третьего, т.е. каждое высказывание или истинно, или
ложно и не может быть одновременно и истинным, и ложным.
В алгебре логики все высказывания обозначают буквами: a, b, c и т.д.
Простейшими операциями в алгебре логики являются операции
логического
сложения (иначе, операция ИЛИ, операция дизъюнкции) и логического умножения
(иначе операция И, операция
конъюнкции). Для обозначения операции логического
сложения используют символы + или
∨
, а логического умножения – символы * или
∧
.
В алгебре логики вводится ещё одна операция –
операция отрицания (иначе НЕ,
операция
инверсии), обозначаемая чертой над элементом.
По определению:
.01;10;0;1 ===∗=+ aaaa
С помощью этих трех функций можно представить (аналитически выразить) любую
сколь угодно сложную логическую функцию.
Функция в алгебре логики – это алгебраическое выражение, содержащее элементы
алгебры логики a, b, c …, связанные между собой операциями, определенными в этой
алгебре.
Например,
cacbaacbaf ++∗∗+=),,(
.
Правила выполнения операций в алгебре логики определяются рядом аксиом, теорем
и следствий.
Перечислим
законы алгебры логики:
• сочетательный (или ассоциативный)
);()(
);()(
cbacba
cbacba
∗∗=∗∗
++=++
• переместительный (или коммутативный)
;
;
abba
abba
∗=∗
+=+
• распределительный
(или дистрибутивный)
;
;)(
cabacba
cabacba
∗+∗=∗+
∗
+
∗=+∗

30
• двойственности (или де Моргана)
;
;
baba
baba
+=∗
∗=+
• двойного отрицания
aa =
• поглощения
abaa
abaa
=+∗
=++
)(
;
• склеивания
.)()(
;
ababa
ababa
=+∗+
=∗+∗
Программное управление ЭВМ
Структура и виды команд в ЭВМ
Решение задач на ЭВМ реализуется программным способом, т.е. путем выполнения
последовательно во времени отдельных операций над информацией, предусмотренной
алгоритмом решения задачи.
Алгоритм – это точно определенная последовательность действий, которые
необходимо выполнить над исходной информацией, чтобы получить решение задачи.
Алгоритм решения задачи, заданный в виде последовательности команд на языке
вычислительной машины (в кодах машины), называется машинной программой.
Команда машинной программы (иначе, машинная команда) – это элементарная
инструкция машине, выполняемая ею автоматически без каких-либо дополнительных
указаний и пояснений.
Машинная команда состоит из двух частей: операционной и адресной.
Операционная часть команды – это группа разрядов в команде, предназначенная для
представления кода операции машины.
Адресная часть команды - это группа разрядов в команде, в которой записываются
коды адреса (адресов) ячеек памяти машины или иных объектов, задействованных при
выполнении команды.
По количеству адресов, записываемых в команде, команды делятся на безадресные,
одно-, двух- и трехадресные.
Типовая структура
трехадресной команды:
КОП a1 a2 a3
КОП – код операции;
a1 и a2 – адреса ячеек (регистров), где расположены соответственно первое и второе
числа, участвующие в операции;
a3 - адрес ячейки(регистра), куда следует поместить число, полученное в
результате выполнения операции.
В
двухадресной команде a1 и a2 выполняют ту же функцию, что в трехадресной
команде. По завершении операции результат помещается в а1.
