Казаринов Л.С., Попова О.В., Барбасова Т.А. Автоматизированные информационно-управляющие системы (часть 1)

Подождите немного. Документ загружается.

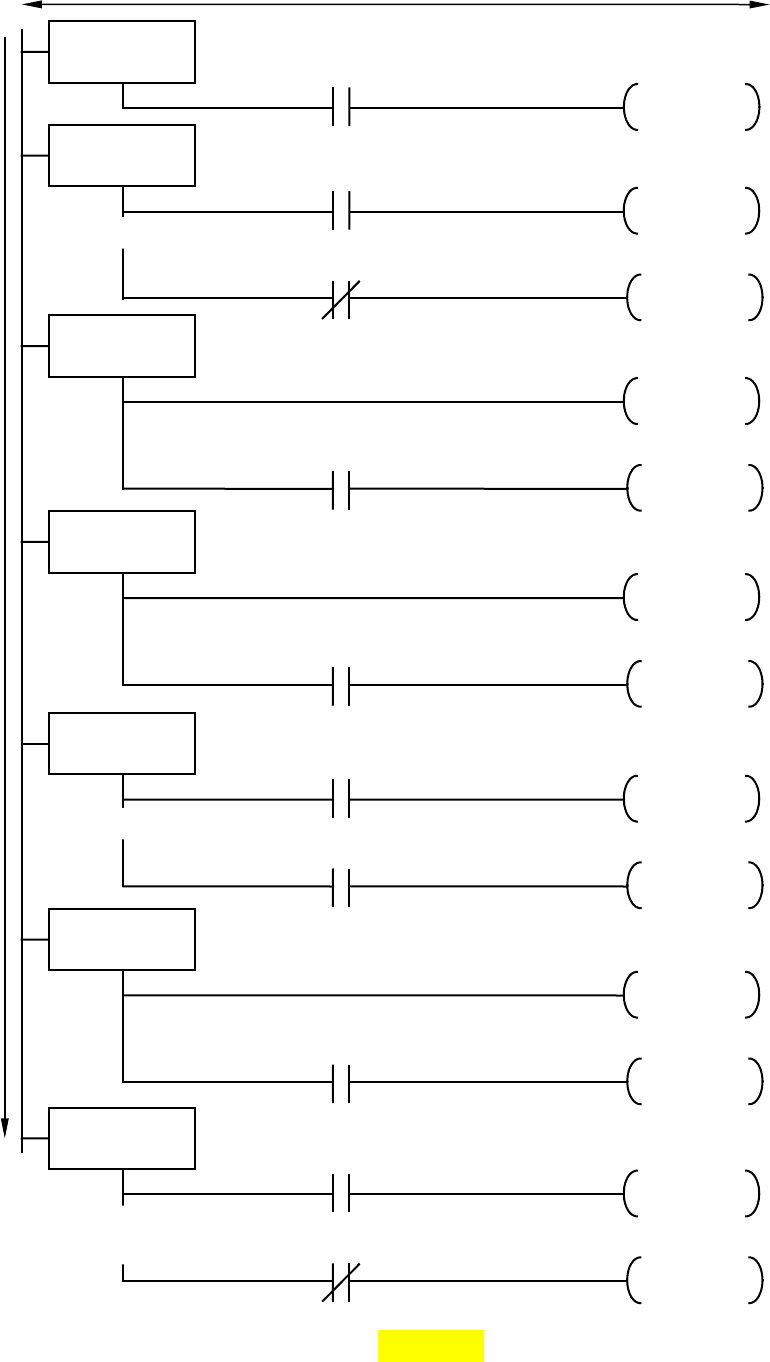
Рис. 3.18

ISG

S0000

Start

Wait for start

JMP

S0001

Part present

Check for part

JMP

Part present

JMP

S0003

Press the part

Press

down

X1SG

S0002

Lock the clamp

Clamp

Set

Part locked

JMP

Lower limit

JMP

S0004

Top limit

Unlock the clamp

Clamp

RST

Part unlocked

JMP

S0005

Index of conveyor

Move

conveyor

Conveyor moved

JMP

S0006

One cycle

One cycle of automatics?

JMP

One cycle

JMP

Only executes logic in stages that are active

131

3.3.3. Пример реализации секвенциально-логических алгоритмов в TRACE

MODE

Язык функциональных блоков (Техно FBD) TRACE MODE содержит

язык Техно LD (Ladder Diagram), который позволяет реализовать

секвенциально-логические алгоритмы на языке стандартной релейной

логики RLL.

Язык функциональных блоков TRACE MODE является языком

визуального программирования. Программа в нем разрабатывается

размещением функциональных блоков с заданными функциями в поле

редактирования, настройкой их входов и выходов, и связи их между собой

в диаграмму, реализующую требуемую функцию.

Рассмотрим основные функции языка LD, реализуемые в TRACE

MODE. Они реализуются с помощью блоков, которые могут быть

представлены как в окне LD программы, так и в окне FBD программы. В

окне LD программы блоки имеют представление и средства

редактирования, соответствующие стандарту языка LD. Рассмотрим

описание блоков в окне FBD программы и в окне LD программы.

Таблица 3.1

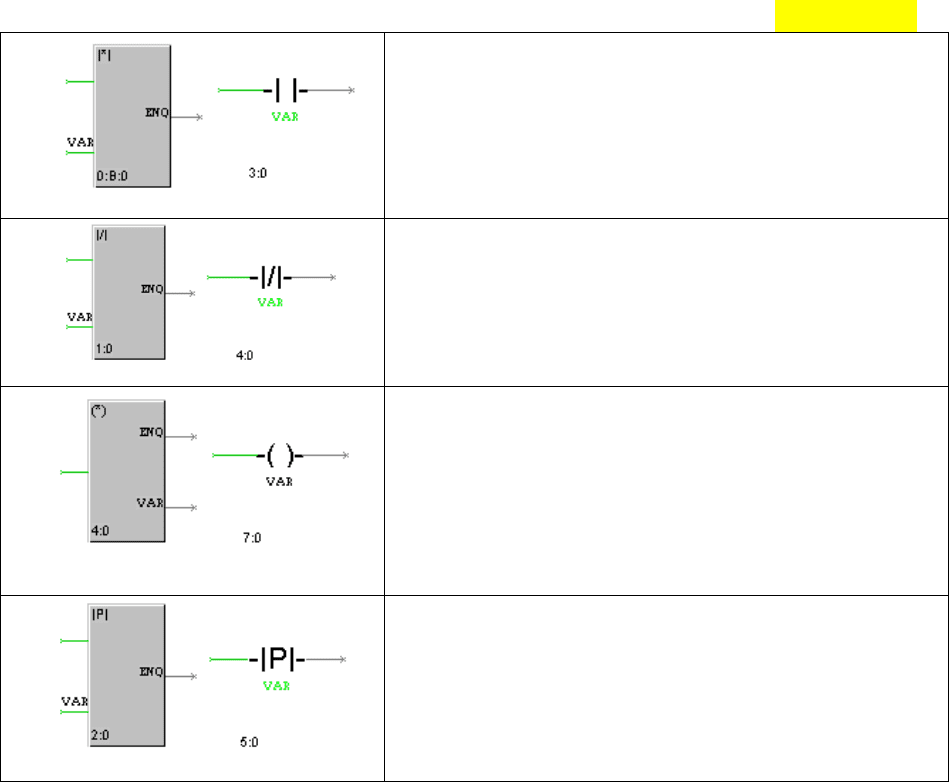
Разомкнутый контакт (| |)

Если VAR<>0, ENQ=RUN (на вход RUN можно

подавать только неотрицательные значения). Если VAR=0,

ENQ=0.

Замкнутый контакт (|/|)

Если VAR=0, ENQ=RUN (на вход RUN можно

подавать только неотрицательные значения). Если VAR<>0,

ENQ=0.

Катушка (( ))

Блок передает неотрицательное значение входа на

выходы ENQ и VAR..

Контакт по положительному переходу (|P|)

Если RUN<>0, а вход VAR меняет свое значение с 0

на любое ненулевое, то на один (следующий) такт пересчета

ENQ=1. Во всех остальных случаях ENQ=0.

132

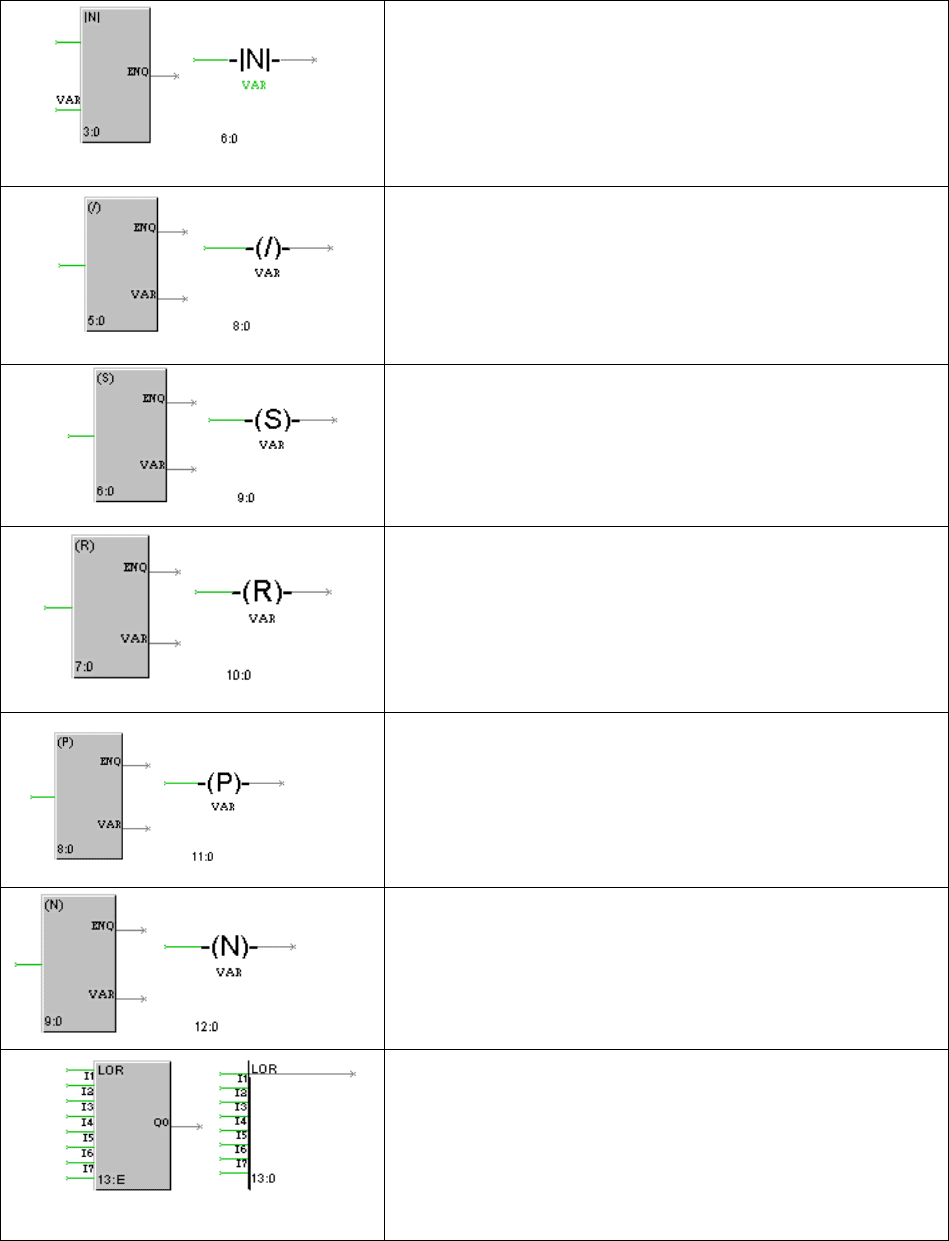
Контакт по отрицательному переходу (|N|)

Если RUN<>0, а вход VAR меняет свое значение с

любого ненулевого на 0, то на один (следующий) такт

пересчета ENQ=1. Во всех остальных случаях ENQ=0.

Инверсная катушка ((/))

Если значение входа больше нуля, VAR=0. Если

значение входа равно нулю, VAR=1. Значение входа всегда

передается на выход ENQ.

Катушка установки ((S))

Значение выхода VAR устанавливается в 1 при подаче

на вход любого ненулевого значения. В дальнейшем

значение выхода VAR не зависит от значения входа.

Катушка сброса ((R))

Значение выхода VAR устанавливается в 0 при подаче

на вход любого ненулевого значения. В дальнейшем

значение выхода VAR не зависит от значения входа.

Катушка положительного перехода ((P))

Если значение входа изменяется с 0 на любое

положительное, то на один (следующий) такт пересчета

VAR=1. Значение входа всегда передается на выход ENQ.

Катушка отрицательного перехода ((N))

Если значение входа изменяется с любого

положительного на 0, то на один (следующий) такт

пересчета VAR=1. Значение входа всегда передается на

выход ENQ.

Блок логического сложения (LOR)

Q0=1, если хотя бы один из входов блока отличен от

нуля. Если значения всех входов равны нулю, Q0=0.

При программировании ПЛК в ТРЕЙС МОУД следует учитывать

особенности редактирования в окне ’LD программы’

В окне LD программы для блоков раздела LD-функции существуют

следующие дополнительные элементы и средства редактирования:

1. Отображение связи входов.

133

Соединенные входы принимают тип, индекс и значение входа, к

которому проведена связь. Если значение соединенных входов равно нулю

или тип таких входов - аргумент, связь невидима. Кроме того, связь видима

только в том случае, если блоки расположены один под другим. Чтобы

удалить связь, нужно вручную изменить индекс одного из соединенных

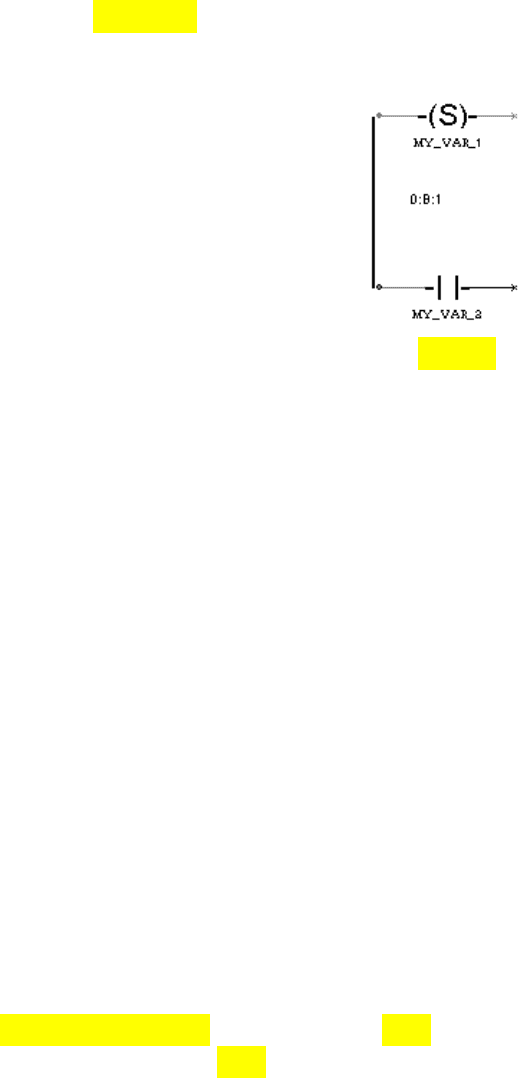
входов. Это свойство может быть использовано для прорисовки левой

шины питания, предусмотренной стандартом языка LD. Для этого надо

расположить блоки один под другим, задать ненулевое значение входа

одного из них, установить тип этого входа константа и далее провести к

этому входу связь от входа другого блока. Результат описанной процедуры

показан на рис. 3.19.

2. Правая шина питания. Эту функцию выполняет блок LOR.

Рис. 3.19

3. Особенности комментария к связанной переменной.

Связанная переменная настраивается таким же образом, как вход или

выход блока. Комментарий выводится на блоке вместо заданного по

умолчанию слова "VAR". Знак ";" выполняет в комментарии функцию

разделителя – на блок выводится текст до этого знака (не более 10

символов).

4. Установка привязки нескольких блоков к одной переменной.

Связанные переменные можно соединять так же, как входы или выходы

блоков. Результат такого действия может быть различным:

 при соединении переменных блоков-контактов итоговая

переменная принимает тип, индекс и значение переменной, к которой

проведена связь;

 при соединении переменных контакта и катушки итоговая

переменная принимает тип и индекс переменной катушки;

 при соединении переменных катушек в диаграмму блоков

добавляется блок LOR, к входам которого автоматически подключаются

соединяемые переменные.

Программа RLC контроллера, построенная для устройства

проштамповки готовых изделий, составленная в TRACE MODE изображена

на рис. 3.20 и 3.21. На рисунке 3.20 изображена программа в окне LD

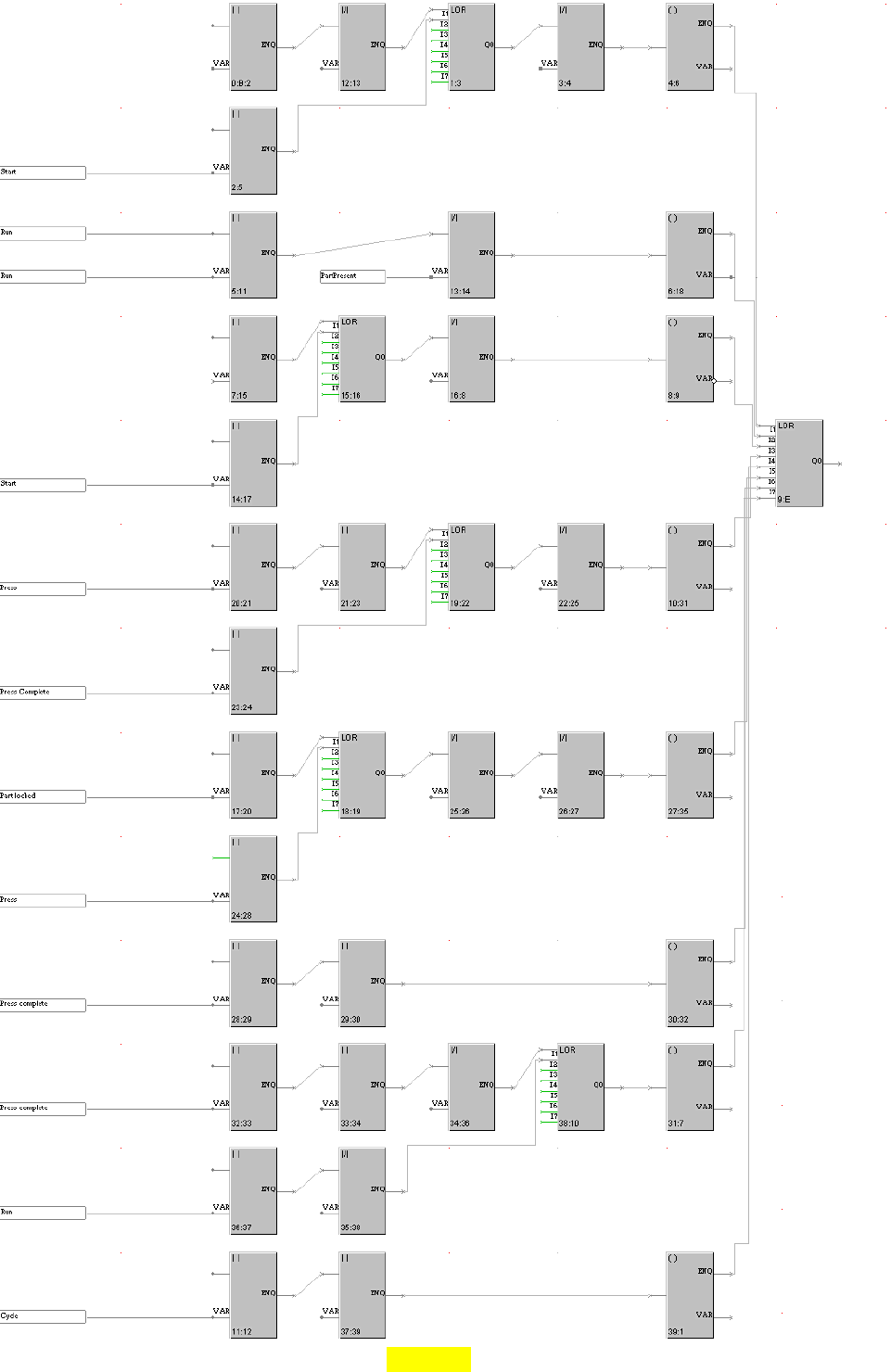
программы, а на рис. 3.21 – в окне FBD программы.

134

135

Рис. 3.20

136

Рис. 3.21

3.4. Средства идентификации и оптимизации

3.4.1. Идентификация характеристик технологических объектов

Идентификация технологического объекта представляет собой

получение (уточнение) по экспериментальным данным модели объекта,

работоспособной для всех эксплуатационных режимов. Для решения задач

идентификации может быть использована многочисленная группа методов, в

частности, регрессионный анализ (РА), корреляционный анализ (КА),

дисперсионный анализ (ДА), диаграмма рассеяния (ДР), проверки

статистических гипотез (ПСГ) и др. Каждый из этих методов имеет свои

разновидности. Например, в методе РА выделяют случаи линейный и

нелинейный РА, одномерный и многомерный РА. Метод ДА подразделяется на

однофакторный, двухфакторный, трехфакторный и т.д. Каждый метод

эффективен для решения определенной группы задач. Так при анализе

существенности влияния факторов на выходной показатель при большом числе

факторов и значительном изменении Q удобно использовать метод диаграмм

рассеяния, если же число факторов невелико и колебания Q незначительны, то

эффективнее метод ДА.

При решении идентификации моделей важное значение имеет точность

определения значений входных переменных Х. Если ошибками в определении

Х можно пренебречь, то можно использовать методы РА, если же значения Х

рассматриваются как случайные величины, то применяются методы КА.

Методы ПСГ используются в различных задачах, связанных с анализом

случайных величин (идентификация закона распределения случайной

величины, проверка существенности различий между параметрами

распределения), построением доверительных интервалов, оценки степени

согласованности мнений экспертов и др.

3.4.2. Идентификация характеристик технологических объектов с

использованием стандартных методов Excel

Суть и этапы регрессионного анализа

Регрессионный анализ заключается в определении аналитического

выражения связи зависимой случайной величины Y (называемой так же

результативным признаком) с независимыми случайными величинами X

, X

…X

(называемыми так же факторами).

Форма связи результативного признака Y с факторами X

, X

,…X

получила название уравнения регрессии. В зависимости, от типа выбранного

уравнения различают линейную и нелинейную регрессию (в последнем случае

возможно дальнейшее уточнение: квадратичная, экспоненциальная,

логарифмическая и т.д.).

В зависимости от числа взаимосвязанных признаков различают парную и

множественную регрессию. Если исследуется связь между двумя признаками

(результативным и факторным), то регрессия называется парной, если между

тремя и более признаками – множественной (многофакторной) регрессией.

137

При изучении регрессии следует придерживаться определенной

последовательности этапов:

1. Задание аналитической формы уравнения регрессии и определение

параметров регрессии.

2. Определение в регрессии степени стохастической взаимосвязи

результативного признака и факторов, проверка общего качества уравнения

регрессии.

3. Проверка статической значимости каждого коэффициента уравнения

регрессии и определение их доверительных интервалов.

Основное содержание этапов регрессионного анализа

Основное содержание выделенных этапов рассмотрим на примере

множественной линейной регрессии, реализованной в режиме «Регрессия»

надстройки Пакет анализа Microsoft Excel.

Этап 1. Уравнение линейной множественной регрессии имеет вид

xaxaxaay  ...

22110



, (3.45)

где



– теоретические значения результативного признака, полученные

путем подстановки соответствующих значений факторных признаков в

уравнение регрессии;

xxx ,...,,

– значения факторных признаков;

aaa ,...,,

– параметры уравнения (коэффициенты регрессии).

Параметры уравнения регрессии могут быть определены с помощью

метода наименьших квадратов (именно этот метод используется в Microsoft

Excel). Сущность данного метода заключается в нахождении параметров

модели (a

), при которых минимизируется сумма квадратов отклонений

эмпирических (фактических) значений результативного признака от

теоретических, полученных по выбранному уравнению регрессии, т.е.

 





mimiiiii

xaxaxaayyyS

22110

min)...()(



. (3.46)

Рассматривая S в качестве функции параметров a

и проводя

математические преобразования (дифференцирование), получаем систему

нормальных уравнений с m неизвестными (по числу параметров a













  

  

,...

............................................................................................

;...

22110

11122

1110

22111

mmmmmm

yxxaxxaxxaxa

yxxxaxxaxaxa

yxaxaxana

(3.47)

где n – число наблюдений;

m – число факторов в уравнении регрессии.

Решив систему уравнений, находим значения параметров a

, являющихся

коэффициентами искомого теоретического уравнения регрессии.

Этап 2. Для определения величины степени стохастической взаимосвязи

результативного признака Y и факторов X необходимо знать следующие

дисперсии:

- общую дисперсию результативного признака Y, отображающую влияние

как основных, так и остаточных факторов:

138









)(



, (3.48)

где



– среднее значение результативного признака Y;

- факторную дисперсию результативного признака Y, отображающую

влияние только основных факторов:









)(





; (3.49)

- остаточную дисперсию результативного признака Y, отображающую

влияние только остаточных факторов:

)1(

)(















. (3.50)

При корреляционной связи результативного признака и факторов

выполняется соотношение

yФ





, при этом

222

OФy





. (3.51)

Для анализа общего качества уравнения линейной многофакторной

регрессии используют обычно множественный коэффициент детерминации

, называемый также квадратом коэффициента множественной корреляции

R. Множественный коэффициент детерминации рассчитывается по формуле





(3.52)

и определяет долю вариации результативного признака, обусловленную

изменением факторных признаков, входящих в многофакторную

регрессионную модель.

Так как в большинстве случаев уравнение регрессии приходится строить

на основе выборочных данных, то возникает вопрос об адекватности

построенного уравнения генеральным данным. Для этого проводится

проверка статической значимости коэффициента детерминации R

на основе

F-критерия Фишера:









, (3.53)

где n – число наблюдений;

m – число факторов в уравнении регрессии.

Примечание. Если в уравнении регрессии свободный член а

= 0, то

числитель n-m-1 следует увеличить на 1, т.е. он будет равен n-m.

В математической статистике доказывается, что если гипотеза H

: R

0 выполняется, то величина F имеет F-распределение с k = m и l = n-m-1

числом степеней свободы, т.е.

)1,(









mnlmkF

. (3.54)

139

Гипотеза H

: R

= 0 о не значимости коэффициента детерминации R

отвергается, если

кр

прp





При значениях R

>0,7 считается, что вариация результативного признака

Y обусловлена в основном влиянием включенных в регрессионную модель

факторов X.

Этап 3. Возможна ситуация, когда часть вычисленных коэффициентов

регрессии не обладает необходимой степенью значимости, т.е. значения

данных коэффициентов будут меньше их стандартной ошибки. В этом случае

такие коэффициенты должны быть исключены из уравнения регрессии.

Поэтому проверка адекватности построенного уравнения регрессии наряду с

проверкой значимости коэффициента детерминации R

включает в себя так

же и проверку значимости каждого коэффициента регрессии.

Значимость коэффициентов регрессии проверяется с помощью t-

критерия Стьюдента:





, (3.55)

где



– стандартное значение ошибки для коэффициента регрессии

В математической статистике доказывается, что если гипотеза H

: a

= 0

выполняется, то величина t имеет распределение Стьюдента с k = n-m-1

числом степеней свободы, т.е.

)1(  mnkt



. (3.56)

Гипотеза H

: a

= 0 о незначимости коэффициента регрессии

отвергается, если

крp

tt 

Кроме того, зная значение t

кр

, можно найти границы доверительных

интервалов для коэффициентов регрессии:

;

max

min

aкрii

taa







(3.57)

Для работы с регрессией открываем вкладку Сервис –> Анализ данных –>

Регрессия (см. рис. 3.22.).

140