Касаева Т.В. и др. Статистика
Подождите немного. Документ загружается.

61
5. Если все варианты ряда уменьшить (увеличить) в А раз, то
средняя уменьшается (увеличивается) в А раз.
Это означает, что
∑
∑
=
f
xf
x
можно исчислять как
A
f
A
x
x *
∑
∑
=
либо
A
f
fxA
x /
*
∑
∑
=
.
6. Если все варианты ряда уменьшить (увеличить) на одно и то же
число х
0
, то и средняя величина уменьшиться (увеличиться) на х
0
∑
∑
=
f
xf
x
, то
есть может быть рассчитана как
( )
0
0
*
x
f
fxx
x
+
−
=
∑
∑
либо
( )
0
0
*
x
f
fxx
x
−
+
=
∑
∑
.
7. Если все частоты ряда разделить (умножить) на одно и то же
число b, то средняя не изменится, то есть
∑
∑
=
f
xf
x
может быть
рассчитана как
∑
∑
=
b
f
b
f
x
x
*
либо как
bf
bxf
x
*
*
Σ
Σ
=
Последние три свойства из перечисленных могут использоваться
одновременно для упрощения расчетов, и тогда считается, что средняя
рассчитывается по «способу моментов» или «методом отсчета от
условного нуля». В данном случае важен факт правильного выбора А
(чаще всего это величина интервала) и х
0
Исчисление средней по «способу моментов» производится по
формуле, вид которой меняется в зависимости от порядка применения
свойств:
(чаще всего это середина
какого-либо интервала).
0
0
*
*
xA
b
f
b
f
A
xx
x +
−
=
∑
∑
либо
Ax
b
f
b
f
x
A
x
x *
*
0
0
+
−
=
∑
∑
и т.д.

62
Независимо от того, применяются либо не применяются свойства
средней величины, результат расчета средней остается неизменным.
Например, необходимо определить среднюю заработную плату
работников организации, в т.ч. по «способу моментов».
Таблица 5.9 – Расчет средней заработной платы
ЗП,
тыс. руб., х
Число
раб-
ков,
f
x
xf
x-x
(x
0
0
A
xx
0
−
=1300)
(A=200)
b
f
(b=20)
b
f
A
xx
*
0
−
800
−
1000
1000 −1200
1200
−1400
1400
−1600
1600
−1800
1800
−
2000
20
80
160
80
40
20
900
1100
1300
1500
1700
1900
18000
88000
208000
120000
68000
3800
-400
-200
0
200
400
600
-2
-1
0
1
2
3
1
4
8
4
2
1
-2
-4
0
4
4
3
Σf=400
Σ xf=
540000
Σ
b
f
=20
Σ
b
f
A
xx
*
0
−
=5
Без использования свойств средней величины:
..1350
400
540000
*
рубтыс
f
fx
x ==
′
=
∑
∑
С использованием свойств средней величины:
0
0
*
*
xA
b
f
b
f
A
xx
x +
−
=
∑
∑
..13501300200*
20
5
рубтысx =+=
5.4 Мода и медиана, способы их вычисления и сфера
применения
Мода и медиана относятся к структурным средним и применяются
для изучения внутреннего строения рядов распределения признака.
Мода (
µ
0
Например, стаж работы, лет, Х: 5, 2,10,15, 2, 5, 7, 8, 5. µ
) − это наиболее часто встречающаяся величина признака
в вариационном ряду.
0
= 5.

63
В дискретном ряду моду будет представлять то значение признака
(та варианта), которое имеет наибольшую частоту.
Например, какое число детей в семье встречается наиболее часто:
Число
детей
х
0
1
2
3
4
5
Число
семей
f
8
12
f
9
max
6
4
1
µ
о
= 1.
Для расчета моды в интервальном ряду вначале определяется
модальный интервал, т.е. интервал, имеющий наибольшую частоту.
Затем рассчитывают моду по формуле
( ) ( )
,
100100
100
00
+−
−
−+−
−
+=
µµµµ
µµ
µµ
µ
ffff
ff
ix
o
где
0
µ
x
− начальная граница модального интервала,
o
i
µ
− ширина модального интервала,
o
f
µ
− частота модального интервала,
1−o
f
µ
− частота интервала, предшествующего модальному,
1+o
f
µ
− частота интервала, следующего за модальным.
Например, определить, с какой численностью работающих чаще
всего встречаются предприятия (организации) в данной отрасли.
Таблица 5.10 – Группировка предприятий по числу работающих
Группы предприятий
по числу работающих
Количество
предприятий в
группе
x
f
500 −1000
1000 −1500
1500 − 2000
5
10
15
-модальный интервал
2000 − 2500
2500 − 3000
14
6
Всего
50=Σf
64
( ) ( )
.1916
14151015
1015
5001500
0
чел=
−+−
−
+=
µ
Следовательно, мода в характеристике рядов распределения
указывает то значение, которое встречается чаще других. Она может
быть определена с помощью полигона: самая высокая точка полигона
указывает на оси абсцисс (х) то значение, которое является модой.
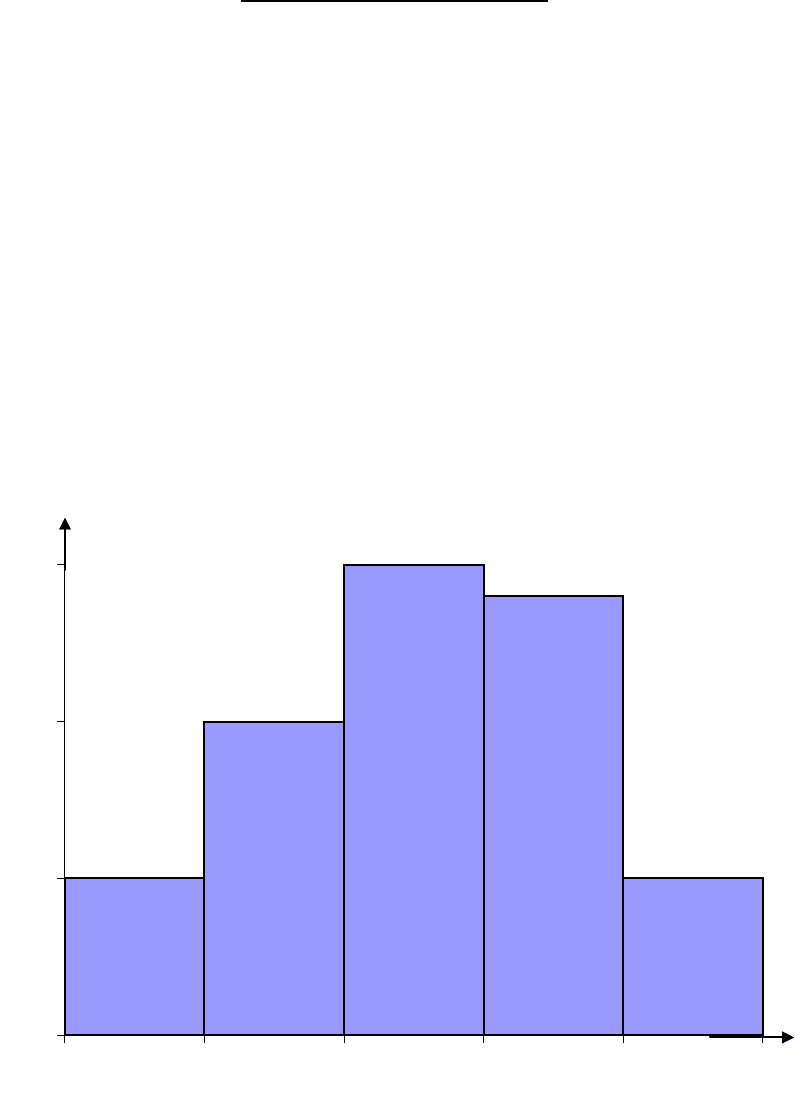
При определении моды в интервальном ряду графическим
способом на гистограмме внутри прямоугольника с наибольшей
частотой проводят две линии:
1 − соединяет его правый верхний угол с правым верхним углом
предшествующего столбика.
2 − соединяет его левый верхний угол с левым верхним углом
следующего.
Абсцисса их точки пересечения и есть мода.
0
5
10
15
500 1000 1500 2000 2500
Рисунок 5.1 – Определение моды в интервальном ряду графическим
способом
Медиана (µ
е
Например, стаж работы, лет (х): 5, 2, 10, 15, 2, 5, 7, 8, 5.
) – это величина варьирующего признака, которая
находится в середине ранжированного ряда.
Вначале ранжируем ряд:
х: 2, 2, 5, 5, 5, 7, 8, 10, 15
µ
е
3000
= 5
f
x

65
Т.е. медиана делит ряд на 2 части, равные по численности.
Половина значений меньше (либо равны) медианы, а вторая – больше
(либо равны). Если ряд состоит из нечетного количества уровней
(вариант), то порядковый номер медианы в ранжированном ряду:
.
2
1+
=
n
№
e
µ
В нашем примере
ый−=
+
5
2
19
Если же ряд состоит из четного количества уровней, то медиана
определяется как средняя арифметическая из варианты под
2
n
№ =
и
варианты
1
2
+=
n
№
.
Например, х, 2, 2, 4, 5, 5, 5, 7, 8, 10, 10, 15, 18
6
2
=
n
, x
6
7
1
2
=+
n
= 5; , x
7
Следовательно, в данном случае:
= 7.
лет
e
6
2
75
=
+
=
µ
При определении медианы в дискретном ряду используют способ
накопления частот. Частоты накапливают до тех пор, пока сумма
накопленных частот (S
µe
Например, определить медиану заработной платы работников.
) не будет равна или больше половины суммы
всех частот (Σf). Последняя накопленная частота и будет указывать то
значение признака, которое является медианой.
Таблица 5.11 – Определение медианы в дискретном ряду
ЗП, тыс. руб.
Число работников, чел.
S
µе
х
f
400
480
600
2
6
16
2
8
24
680
800
12
4
Σf = 40
µ
e
В случае, если сумма накопленных частот составила ровно
половину всех частот, медиана определяется как средняя из данного
уровня и следующего за ним.
= 600 тыс.руб.

66
Таблица 5.12 – Определение медианы в дискретном ряду
ЗП, тыс. руб.
Число работников, чел.
S
µе
х
f
400
480
600
2
6
12
2
8
20
680
800
16
4
Σf = 40
Для определения медианы в интервальном ряду вначале с
помощью суммы накопленных частот определяют медианный интервал,
а затем рассчитывают медиану по формуле
,
5.0
1
e
e
ee
f
Sf
ix
e
µ
µ
µµ
µ
∑
−
−
+=
где Х
µе
i
− начальная граница медианного интервала;
µe
f
− ширина медианного интервала;
µe
S
− частота медианного интервала;
µe-1
Например, определить медиану численности работников
предприятия (организации).
− сумма накопленных частот интервала, предшествующего
медианному.
Таблица 5.13 – Исходные данные для расчета медианы численности
работников
Группы предприятий
по числу работников
Количество
предприятий
S
µе
х
f
500 − 1000
1000 − 1500
1500 − 2000
5
10
15
5
15
30
медианный интервал
2000 − 2500
2500 − 3000
14
6
44
50
Σf = 50
.1833
15
1550*5.0
5001500 чел
e
=
−
+=
µ
Для графического определения медианы используют кумуляту:
последнюю ординату кумуляты делят пополам и через полученную
..640
2
680600
рубтыс
e
=
+
=
µ

67
точку проводят прямую параллельную оси абсцисс. Абсцисса точки
пересечения этой прямой с кумулятой и есть медиана.
0
5
10
15
20
25
30
35
40
45
50
55
60
500 1000 1500 2000 2500 3000
Рисунок 5.2 – Определение медианы графическим способом
х
S
µe
µ
e
=1833
2
1
2
1

68
6 СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ ВАРИАЦИИ
6.1. Понятие вариации и необходимость её статистического
изучения.
6.2. Показатели вариации.
6.2.1 Абсолютные показатели вариации.
6.2.2 Относительные показатели вариации.
6.3. Дисперсия, её виды и свойства.
6.1 Понятие вариации и необходимость её статистического
изучения
Вариацией признака
С другой стороны,
называется его изменение при переходе от
одной единицы наблюдения к другой.
вариация – это то, что порождает
необходимость статистики
После того, как исчислена средняя величина, возникает вопрос о
её надёжности или её типичности. При этом необходимо учитывать, что
типичность средней находится в обратной зависимости от вариации
(колеблемости) уровней признака: чем больше вариация уровней
исходной информации, тем меньше типичность (представительность,
репрезентативность) средней величины. В случае слишком большой
вариации уровней ряда можно получить фиктивную среднюю.
. Как уже отмечалось ранее, лишено смысла
исследование стоимости автобусного билета в городе Витебске, так как
это явление не варьирующее.
Рассмотрим два примера, в которых уровни средних величин
равны, но эти средние имеют разные представительности.
Пример: имеется информация о выработке рабочих двух цехов.
Таблица 6.1 – Распределение рабочих цеха № 1 по уровню выработки
деталей в смену
Выработка 1 рабочего
в смену, дет x
Число
рабочих,
чел
f
xf
xx −
xx −
f
( )
2
xx −
( )
2
xx −
f
x
x
2
2
f
30
10
300
14
140
196
1960
900
9000
42
10
420
2
20
4
40
1764
17640
46
10
460
2
20
4
40
2116
21160
58
10
580
14
140
196
1960
3364
33640
∑
= 40f
∑
= 1760xf
=−
∑
fxx
= 320
( )
2
=−
∑
fxx
=4000
81440
2
=
∑
fx
69
Таблица 6.2 – Распределение рабочих цеха № 2 по уровню выработки
деталей в смену
Выра-
ботка 1
рабочего
в смену,
дет x
Число
рабочих,
чел.
f
xf
xx −
xx −
f
( )
2
xx −
( )
2
xx −
f
x
x
2
2
f
40 5 200 4 20 16 80 1600 8000
42
10
420
2
20
4
40
1764
17640
44
10
440
0
0
0
0
1936
19360
46
10
460
2
20
4
40
2116
21160
48
5
240
4
20
16
80
2304
11520
∑
= 40f
∑
= 1760xf
80=−
∑
fxx
( )
240
2
=
−
∑
fxx
∑
= 77680
2
fx
В обоих случаях средняя выработка рассчитывается по формуле
средней арифметической взвешенной:
Цех № 1
.44
40
1760
детали
f
xf
x ===
∑
∑
Цех № 2
.44
40
1760
детали
f
xf
x ===
∑
∑
Однако, анализируя уровни исходной информации, замечаем:
Цех №1 − вариация выработки от 30 до 58 деталей в смену.
Цех №2 − вариация выработки от 40 до 48 деталей в смену.
Следовательно,
=
x
44 наиболее типична для цеха № 2.
Для характеристики степени вариации признака (а следовательно,
для оценки типичности средней величины) в статистике используют
следующие показатели:
1) размах вариации (R);
2) среднее линейное отклонение (l);
3) дисперсия (
2
σ
);
4) среднее квадратическое отклонение (
σ
);
5) коэффициент осцилляции (К
r
6) относительное линейное отклонение (К
);
l
7) коэффициент вариации (V);
);
Первые четыре относятся к абсолютным показателям вариации, а
последние три − к относительным.
Значение показателей вариации заключается в следующем:
1) они дополняют средние величины, за которыми скрываются
индивидуальные различия отдельных единиц совокупности;
2) они характеризуют степень однородности статистической
совокупности по изучаемому признаку;
3) они характеризуют границы вариации признака;

70
4) соотношение показателей вариации может быть использовано
для характеристики взаимосвязи между признаками (см. 6.3).
6.2 Показатели вариации
Показатели вариации относятся к числу обобщающих
показателей, они измеряют вариацию совокупности явлений.
6.2.1 Абсолютные показатели вариации
К числу абсолютных показателей вариации относят:
- размах вариации;
- среднее линейное отклонение;
- дисперсию;
- среднее квадратическое отклонение.
6.2.1.1
Размах вариации – это разность между максимальным и
минимальным значениями признака.
(6.1)
В наших примерах: R
1
R
= 58 – 30 = 28 (дет.)
2
Следовательно, для цеха № 2
= 48 – 40 = 8 (дет.)
=x
44 наиболее типична, чем для
цеха № 1.
Преимущество данного показателя: простота его исчисления.
Недостатки:
1) он не учитывает внутреннюю колеблемость уровней ряда;
2) он часто зависит от случайности. Например, количество
пропущенных часов занятий студентами группы,
Х, 4, 6, 8, 0, 8, 2, 4, 6, 8, 4, 0, 0, 80, 4, 8, 4, 6, 8, 8, 0, 0, 4, 2, 4, 2, 6
R= 80 – 0 = 80 час, хотя на самом деле за исключением одного студента
вся остальная часть совокупности более-менее однородна по пропускам:
0 ÷ 8 час.
Область применения R поэтому ограничивается достаточно
однородными совокупностями. Например, в предупредительном
контроле качества продукции.
6.2.1.2
Однако, учитывая нулевое свойство средней арифметической:
сумма отклонений индивидуальных значений признака от средней
равна 0. Поэтому при исчислении среднего линейного отклонения
суммируются модули этих отклонений.
Среднее линейное отклонение – это средняя
арифметическая величина, исчисленная из абсолютных отклонений
индивидуальных значений признаков от средней величины.
minmax
XXR −=
