Караулов В.Н., Громов А.К.: Испытания синхронных машин. Методические указания к лабораторным работам
Подождите немного. Документ загружается.

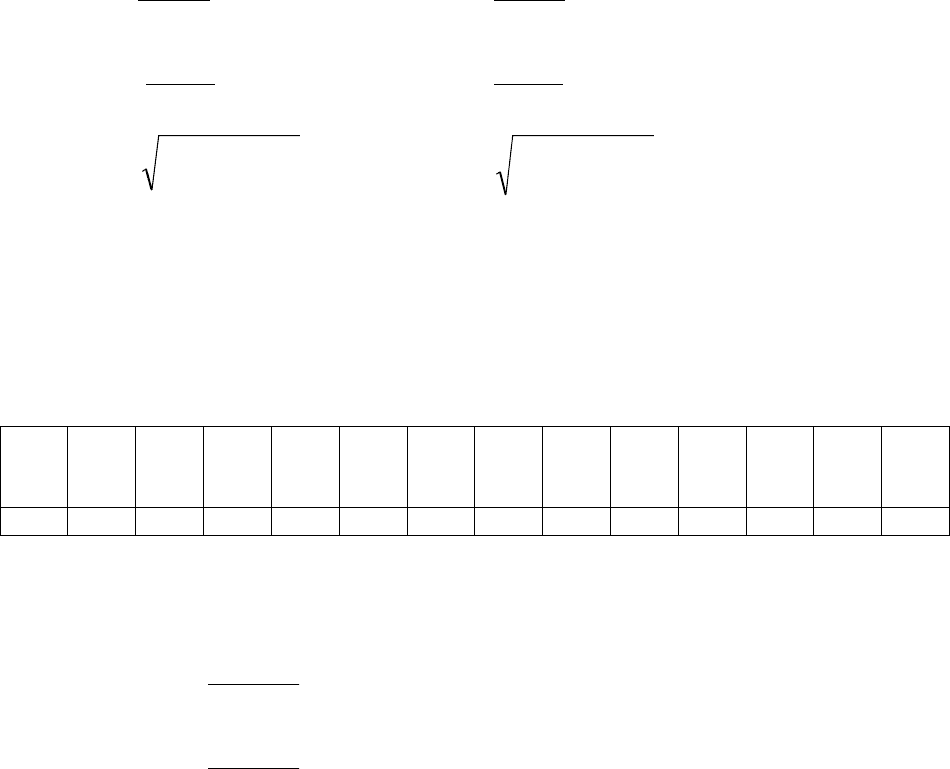
Измерив в этих положениях приложенное напряжение U, ток в обмотке
якоря I и потребляемую мощность Р (табл. 4.4) определяют сопротивления
х
d
'' (х
q
'') по следующим формулам:
max
min
''
d
2I
U
z = , r''
d
=
2
maх
max
I2
P
,
z =
''
q
min
max
I2
U
,
r =
"
q
2
min
min
I2
P
,
() ()
2
"
d
2
"
d
"
d
rzx −= ,
() ()
2
"
q
2
"
q
"
q
rzx −=
. (4.9)
Таблица 4.4.
Сверхпереходные индуктивные сопротивления обмотки якоря по продольной
и поперечной осям х
d
'' и х
q
''
U,
В
I,
А
Р,
Вт
z''
d
,
Ом
r''
d
,
Ом
х''
d
,
Ом
z
b
,
Ом
х''
d
*
,
о.е.
r''
d
*
,
о.е.
z''
q
*
,
о.е.
r''
q
*
,
о.е.
х''
q
*
,
о.е.
х''
q
*
,
о.е.
r''
q
*
,
о.е.
По полученным значениям х
d
'' и х
q
'' может быть рассчитана величина
индуктивного сопротивления обратной последовательности по формулам
х
2
=
2
хx
''
q
''
d
+
, (4.10)
х
2
=
''
q
''
d
''
q
''
d
хx
хx2
+
. (4.11)
Сопротивление х
2
по формуле (4.10) соответствует случаю, когда
напряжения статора синусоидальны, а токи несинусоидальны. Последние
индуцированы в обмотке статора токами ротора двойной частоты. Если
последовательно с обмоткой статора включены значительные индуктивные
сопротивления (например, сопротивления трансформаторов и линии
передачи), то токи статора синусоидальны, а напряжения обмотки статора
несинусоидальны. В этом случае сопротивление х
2
рассчитывают по формуле
(4.11).
Сопротивление х
2
по (4.10) и (4.11) необходимо сравнить со средним
значением х
2
по п. 4.3.
41
Контрольные вопросы
1.
Какие опыты позволяют рассчитать синхронные индуктивные
сопротивления
х
d
и х
q
? Назовите условия и порядок проведения этих
опытов.
2.
Какие опыты позволяют рассчитать параметры обратной
последовательности
х
2
и r
2
? Назовите условия и порядок проведения
этих опытов.
3.
Какие опыты позволяют рассчитать параметры нулевой
последовательности
х
0
и r
0
? Назовите условия и порядок проведения этих
опытов.
4.
Какие опыты позволяют рассчитать сверхпереходные индуктивные
сопротивления
х
d
'' и х
q
''? Назовите условия и порядок проведения этих
опытов.
5.
Назовите режимы работы синхронной машины, при анализе которых
используются найденные параметры.
6.
Сравните и объясните различие числовых значений параметров:
х
d
и х
q
, х
d
'' и х
q
'', х
2
и х
1
, х
1
и х
0
, х
d
'' и х
d
.
7.
Все представленные в работе опыты выполняются при пониженном
значении напряжения. Как это влияет на значения определяемых
параметров?
42
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Вольдек А.И. Электрические машины. Изд. 2–ое. –Л.: Энергия, 1974. –
839 с.
2.
Костенко М.П., Пиотровский Л.М. Электрические машины, В 2 ч.,
ч.2. – Машины переменного тока. –Л.: Энергия, I973–648 с.
3.
Жерве Г.К. Промышленные испытания электрических машин. Л.:
Энергия,1968. . –574 с.: ил.
4.
Гольдберг О.Д. Испытания электрических машин: Учеб. для вузов. –
М.: Высш. шк., 2000. –255 с.: ил.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ ……………………………………………….……………….
1.
ИСПЫТАНИЯ ТРЕХФАЗНОГО СИНХРОННОГО
ГЕНЕРАТОРА ………………………………………………………..
2.
ИССЛЕДОВАНИЕ ПАРАЛЛЕЛЬНОЙ РАБОТЫ С СЕТЬЮ
ТРЕХФАЗНОГО СИНХРОННОГО ГЕНЕРАТОРА ………………
3.
ИСПЫТАНИЯ СИНХРОННОГО ДВИГАТЕЛЯ …………………..
4.
ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ СИНХРОННОЙ МАШИНЫ ….
БИБЛИОГРАФИЧЕСКИЙ СПИСОК ……………………………….…...
3
4
20
27
34
43
43
