Караулов В.Н., Громов А.К.: Испытания синхронных машин. Методические указания к лабораторным работам

Подождите немного. Документ загружается.

соответствии с требованиями стандарта (ГОСТ 10169-77): замыкание фаз

накоротко производится как можно ближе к выводам машины; частота

вращения ротора при определении характеристики трехфазного короткого

замыкания может отличаться от номинальной (но не ниже 0,2 номинальной);

опыты двухфазного и однофазного коротких замыканий проводятся при

скоростях вращения, близких к номинальной. Соответствующие схемы для

снятия характеристик показаны

на рис. 1.6.

При определении характеристики короткого замыкания ротор

генератора вращается со скоростью, близкой к номинальной. Первый отсчет

производится при токе якоря I

кз

≈1,1 I

; затем ток короткого замыкания I

кз

уменьшают, снижая значение тока возбуждения i

. Для каждой из

характеристик достаточно записать 3–4 пары показаний приборов в табл. 1.6.

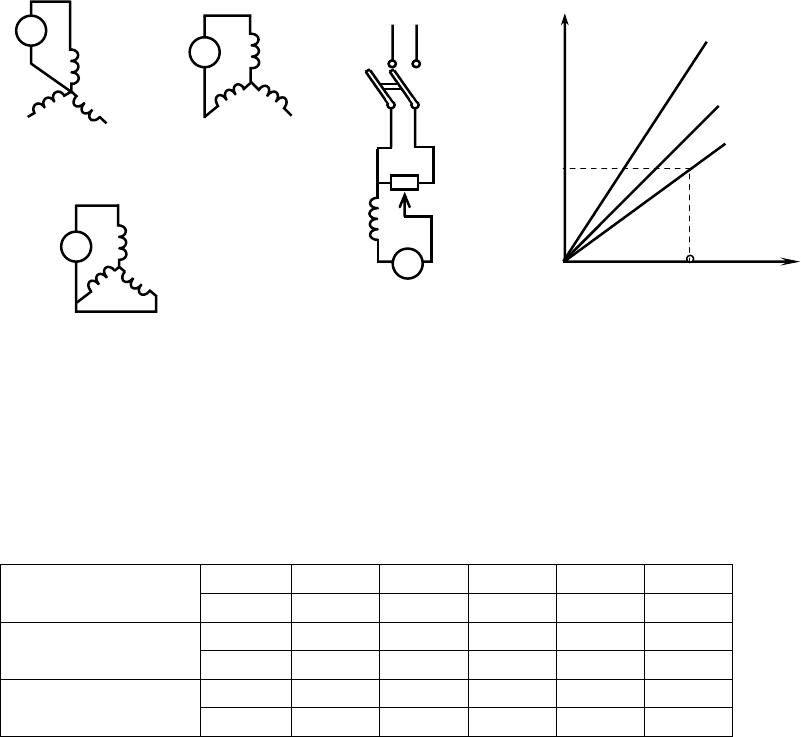
Рис. 1.6. Схемы опытов коротких замыканий Рис. 1.7. Характеристики

коротких замыканий

Таблица 1.6.

Характеристики установившихся коротких замыканий

, А 3 - фазное КЗ

К3

, А

к1

к2

Iк

к3

fк

И2

И1

, А 2 - фазное КЗ

К2

, А

, А 1 - фазное КЗ

К1

, А

Качественный вид характеристик коротких показан на

рис.1.7.

замыканий

При построении и использовании характеристик установившихся

коротких замыканий в системе относительных единиц ток

нф

1.7. Определение синхронного индуктивного сопротивления х

d ненас

в ненасыщенном состоянии магнитной цепи, отношения короткого

замыкания и расчетного индуктивного сопротивления х

I.7.1. Определение ненасыщенного синхронного индуктивного

сопротивления обмотки статора по продольной оси

Ненасыщенное значение синхронного индуктивного сопротивления по

продольной оси обмотки статора х

можно вычислить с помощью

характеристик холостого хода и трехфазного короткого замыкания (ХКЗ).

Нужно построить на одном рисунке ХХХ U

оф

= f (i

) или U*

= f (i

*) и ХКЗ

I=f(i

) или I*=f(i

*) как это показано на рис. 1.8.

Поскольку при трехфазном коротком замыкании генератора реакция

якоря носит почти чисто размагничивающий характер, то результирующий

поток генератора получается очень небольшим и магнитная система

генератора при коротком замыкании не насыщена. Поэтому при определении

индуктивного сопротивления обмотки статора х

dненас

пользуются не

действительной ХХХ, а ее начальной прямолинейной частью или ее

продолжением – линия Oh на рис. 1.8.

Отношение напряжения U

′ по спрямленной ХХХ при величине тока

возбуждения i

к току I

, соответствующему i

по ХКЗ, дает ненасыщенное

значение синхронного индуктивного сопротивления по продольной оси:

ненас

′

= ,

(1.4)

где U

′ и I

– соответственно напряжение и ток в вольтах и в амперах.

В относительных единицах:

ненас

*Xd = ,

(1.5)

где U′* и I

* - напряжение и ток в о.е.

По ХКЗ определяется ток возбуждения i

fк

= ОА, при котором ток

короткого замыкания равен номинальному I

. Точка А является исходной для

ИНХ (см. рис. 1.3 и рис. 1.9.).

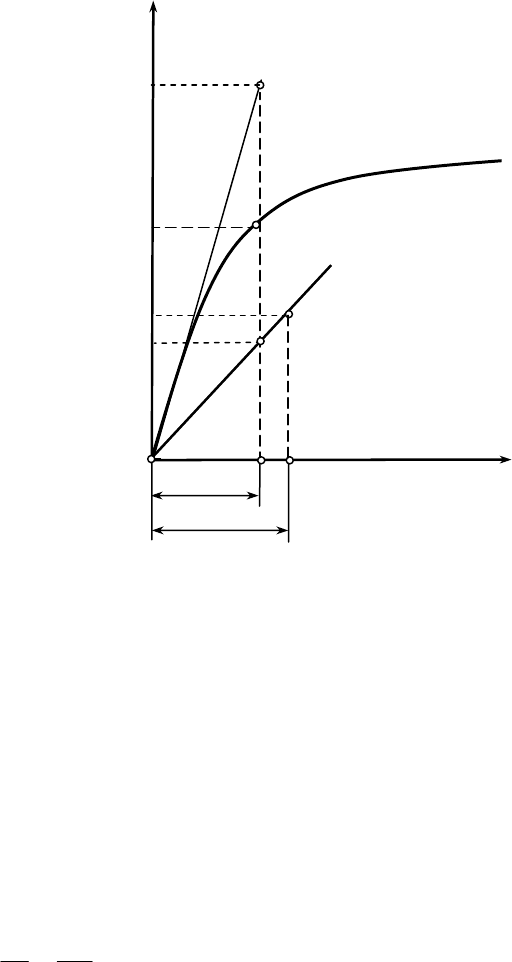
Рис. 1.8. Определение индуктивного сопротивления х

и отношения короткого замыкания

I.7.2. Определение отношения короткого замыкания

Отношением короткого замыкания (ОКЗ) называется отношение тока

трехфазного короткого замыкания I

при токе возбуждения,

соответствующем номинальному напряжению при холостом ходе, к

номинальному току якоря I

(рис. 1.8)

ОКЗ =

ХХХ

′

ХКЗ

O е

fо

fк

= . (1.6)

I.7.3. Определение расчетного индуктивного сопротивления

Расчетное индуктивное сопротивление

можно вычислить с помощью

характеристик холостого хода и индукционной нагрузочной. Нужно

построить на одном рисунке ХХХ (U

оф

= f (i

) или U*

оф

= f (i

*)) и ИНХ

=f(i

) или U

*=f(i

*)) и выполнить построения так, как это показано на

рис.1.9.

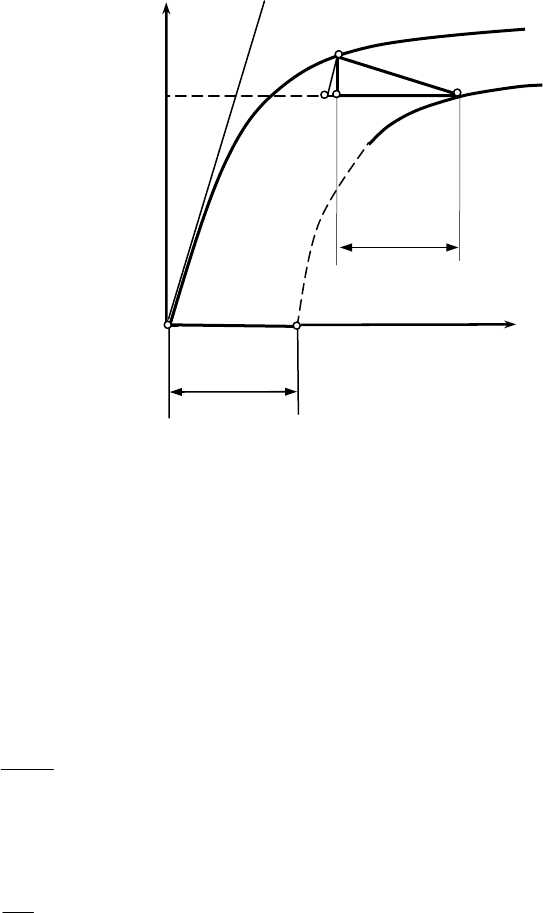
Порядок построений на рис. 1.9:

•

на индукционной нагрузочной характеристике необходимо найти точку А',

соответствующую номинальному значению U

оф

( или U

оф

*);

•

от т. А' влево параллельно оси абсцисс отложить отрезок А'О' = АО (п.

1.7.1);

•

из точки О' параллельно начальной части характеристики холостого хода

провести отрезок О'В' до пересечения с характеристикой холостого хода в

т. В';

•

из точки В' опустить перпендикуляр В'С' на отрезок А'О'.

Рис. 1.9. Определение расчетного индуктивного сопротивления х

В треугольнике А'В'С' катет А'С' соответствует току возбуждения i

fа

* – если характеристики построены в относительных единицах),

компенсирующему размагничивающее действие продольной реакции якоря,

а катет С'В' – падению напряжения в искомом расчетном индуктивном

сопротивлении. Расчетное индуктивное сопротивление равно, Ом,

Uф

оф

ИНХ

B′

O′

fк

А′

′

ХХХ

ВС

′′

= , (I.6)

где С'В' в вольтах.

Полученное значение подсчитывают в относительных единицах

, (1.7)

где базисное сопротивление

нф

нл

z = . (1.8)

Если характеристики ХХХ и ИНХ построены в относительных единицах, то

и значение С'В' определяется в относительных единицах. В этом случае

расчетное индуктивное сопротивление равно, о.е.,

ВС

′′

= . (I.9)

Здесь и далее принимается, что расчетное индуктивное сопротивление

приближенно равно сопротивлению рассеяния обмотки якоря х

σ1

≈

I.8. Определение тока возбуждения при нагрузке генератора

методом графического построения и вычисление насыщенного

значения синхронного индуктивного сопротивления обмотки

статора по продольной оси

I.8.1. Определение тока возбуждения при нагрузке генератора

методом графического построения

Приводимое графическое построение (диаграмма) служит для

определения изменения напряжения при сбросе нагрузки и для определения

тока возбуждения при симметричном режиме нагрузки генератора.

Диаграмма справедлива для насыщенных неявнополюсных машин, но может

быть применена и для явнополюсных машин.

Диаграмма строится для известных напряжения U

, тока I

коэффициента мощности cos ϕ (задается преподавателем). Для построения

диаграммы должны быть известны: сопротивление

, ХХХ U

=f(i

) и МДС

реакции якоря i

в масштабе тока возбуждения (см. рис. 1.9). Диаграмма

может быть построена как в именованных единицах так и в относительных.

Традиционный вид диаграммы показан на рис. 1.10. В технических

требованиях к синхронным генераторам (ГОСТ 10169-77) диаграмма МДС

строится в виде, представленном на рис. 1.11. Диаграмма строится без учета

падения напряжения на омическом сопротивлении фазы İ

так как величина

его в синхронных машинах средней и большой мощности относительно

незначительна.

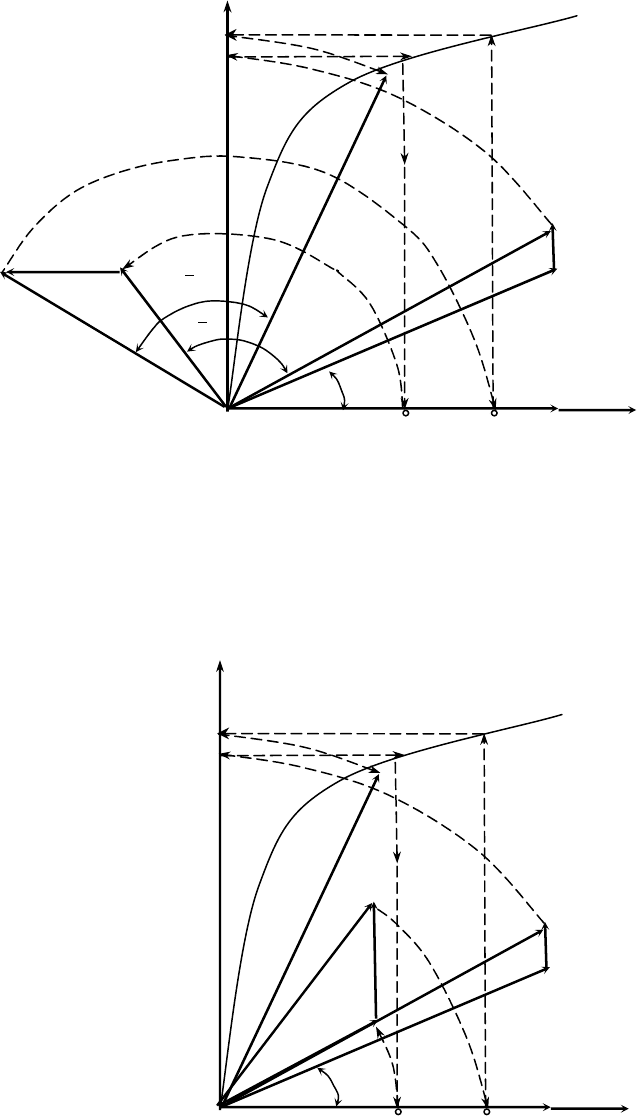
Рис. 1.10. Традиционный вид диаграммы для определения тока возбуждения

синхронной машины при нагрузке

Рис. 1.11. Построение диаграммы МДС

Ỉ

jỈx

fδ

fн

Ủ

нф

．．

ХХХ

．

fδ

fн

jỈx

fδ

-i

fн

Ủ

нф

．．

ХХХ

Ỉ

．

fδ

fн

Для построения диаграммы МДС сначала необходимо выбрать

масштабы для тока и напряжения, чтобы диаграмма разместилась на листе.

Порядок построения диаграммы, представленной на рис. 1.11:

•

по горизонтальной оси откладывается вектор тока якоря İ;

•

под углом ϕ к вектору тока якоря İ в сторону опережения (для активно-

индуктивной нагрузки) откладывается вектор напряжения Ů

нф

;

•

к вектору напряжения нужно прибавить вектор падения напряжения на

расчетном индуктивном сопротивлении jİ

перпендикулярно к вектору

тока в сторону опережения. Полученный вектор Ẻ

представляет собой

ЭДС, которая индуцируется в обмотке якоря результирующим потоком в

зазоре при нагрузке генератора;

•

по характеристике холостого хода определяется величина

результирующего тока возбуждения i

fδ

, соответствующего ЭДС Ẻ

;

•

ток i

fδ

откладывается из начала координат по направлению вектора Ẻ

;

•

из конца отрезка, равного i

fδ

, вверх, перпендикулярно вектору тока якоря

, откладывают составляющую тока возбуждения i

, компенсирующую

реакцию якоря Fa при токе короткого замыкания, равном номинальному

току. Значение Fa равно (i

fа

в масштабе тока возбуждения) отрезку С'А' на

рис. 1.9;

•

отрезок прямой от начала координат 0 до конца отрезка i

дает величину

номинального тока возбуждения i

fн

Если известно число витков w

обмотки возбуждения, то может быть

рассчитана МДС этой обмотки. Тогда в построениях может быть

использовано обозначение МДС i

, а диаграмма имеет название

«диаграмма МДС».

Найденный ток возбуждения i

fн

позволяет с помощью характеристики

холостого хода определить напряжение генератора U

при сбросе нагрузки.

Изменение напряжения генератора

%100

но

⋅

−

=∆ . (1.10)

Найденное значение

U% необходимо сравнить со значением U%,

полученным в п. 1.4.

I.8.2. Вычисление насыщенного синхронного индуктивного

сопротивления обмотки статора по продольной оси

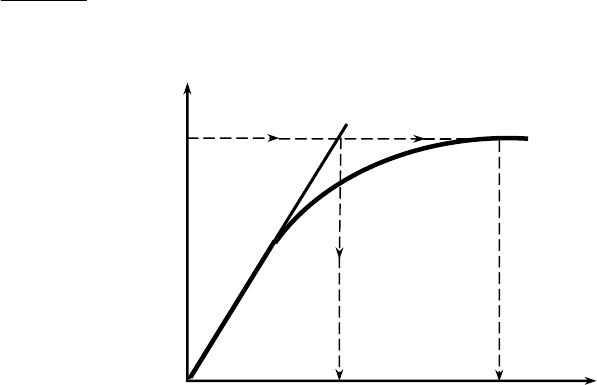
При построении диаграммы определены величины E

и i

fδ

. На рис. 1.12

показана величина i

fδ

соответствующая значению E

. Спрямленная

характеристика холостого хода на рис. 1.12 позволяет определить величину

∆ ∆

тока возбуждения i'

fδ

, соответствующего той же величине ЭДС E

ненасыщенной машине. Степень насыщения магнитной цепи

характеризуется коэффициентом насыщения k

= i

fδ

/ i'

fδ

Насыщение приводит к уменьшению магнитных проводимостей и

соответствующему уменьшению индуктивных сопротивлений. Поэтому

величина насыщенного синхронного сопротивления по продольной оси равна

ненасd

насd

. (1.11)

Рис. 1.12. Определение коэффициента насыщения магнитной цепи

Нарисуйте полюсного и

неявнополюсного синхронного

генератора.

Объясните образование синхронной

машине.

Чем определяется генератора в

режиме холостого

Как снимается объясняется ее

нелинейный характер?

Дайте определение продольной d и поперечной q осей синхронной

машины. Объясните влияние тока якоря на основное магнитное поле при

различном характере нагрузки?

Как снимаются характеристики установившихся коротких замыканий?

Чем объясняется их линейный характер?

fδ

ХХХ

Контрольные вопросы

принципиальное устройство явно

генераторов; объясните принцип действия

электромагнитного момента в

частота и величина ЭДС автономного

хода?

характеристика холостого хода? Чем

7. Перечислите факторы определяющие величину индуктивных

сопротивлений х

аd

и х

аq

Как снимается индукционная нагрузочная характеристика. Почему

индукционная нагрузочная характеристика находится ниже

характеристики холостого хода?

Как определяется начальная точка индукционной нагрузочной

характеристики?

10.

Как определяется ненасыщенное значение синхронного индуктивного

сопротивления по продольной оси?

11.

Как определяется расчетное индуктивное сопротивление?

12.

Как снимаются внешние и регулировочные характеристики при

увеличении нагрузки и снижении нагрузки? Объясните вид этих

характеристик.

13.

Нарисуйте векторные диаграммы напряжений при различном характере

автономных нагрузок явнополюсного генератора.

14.

Как определяется отношение короткого замыкания? Какой

конструктивный размер определяет его величину?

15.

Объясните построение диаграммы МДС.

16.

Как определяется насыщенное значение синхронного индуктивного

сопротивления по продольной оси?

2. ИССЛЕДОВАНИЕ ПАРАЛЛЕЛЬНОЙ РАБОТЫ С СЕТЬЮ

ТРЕХФАЗНОГО СИНХРОННОГО ГЕНЕРАТОРА (2С)

2.1. Программа исследования

Записать паспорт синхронного генератора и приводного двигателя.

Включить генератор на параллельную работу с сетью методом точной

синхронизации.

Провести испытания синхронного генератора при параллельной работе с

сетью в режиме регулирования активной мощности при постоянном токе

возбуждения; испытания провести при двух значениях тока возбуждения

по заданию преподавателя.

Провести испытания синхронного генератора при параллельной работе с

сетью при постоянной активной мощности и переменном возбуждении;

испытания провести при двух значениях отдаваемой активной

мощности:

а) Р

=0; б) Р

=(0,2–0,5) Р

2.2. Включение генератора на параллельную работу с сетью

методом точной синхронизации

Перед включением генератора на параллельную работу добиваются

выполнения следующих условий:

Действующие значения напряжений генератора и сети должны быть

одинаковы U

Частота напряжения генератора должна быть равна частоте

напряжения сети f

= f

Порядок следования фаз у генератора и в сети должен быть

одинаковым.

В момент подключения генератора к сети мгновенные значения

напряжений на одноименных фазах генератора и сети должны быть

одинаковы.

Выполнение перечисленных условий включения генератора на

параллельную работу с сетью называется синхронизацией.

Для проведения опыта собирается схема, представленная на рис. 2.1; в

процессе сборки выбирается и реализуется схема включения лампового

синхроноскопа (рис. 2.2). В качестве двигателя, приводящего во вращение

ротор синхронного генератора, в работе используется двигатель постоянного