Kao M.-Y. (ed.) Encyclopedia of Algorithms

Подождите немного. Документ загружается.

118 B Byzantine Agreement

lows to solve the problem in t +1rounds[23]. An algo-

rithm which terminates in min( f +2; t +1) rounds was

presented in [22]. Uniform agreement is impossible for

t  n/2 [23]. For t < n/2, there is an algorithm that

achieves uniform agreement in min(f +2; t +1) rounds

(and O(n

f ) message complexity) [20].

Byzantine Failures with Authentication

A(t + 1)-round BA algorithm is presented in [12]. An al-

gorithm which terminates in min( f +2; t +1)roundscan

be found in [24]. The message complexity of the problem

is analyzed in [10], where it is shown that the number of

signatures and the number of messages in any authenti-

cated BA algorithm are ˝(nt)and˝(n + t

), respectively.

In addition, it is shown that ˝(nt) is the bound on the

number of messages for the unauthenticated BA.

Byzantine Failures Without Authentication

In the unauthenticated case, the BA problem can be solved

if and only if n > 3t. The proof can be found in [1,19].

An algorithm that decides in min(f +3; t +1)rounds(it

might require two additional rounds to stop) is presented

in [16]. Unfortunately, this algorithm is complicated.

Simpler algorithms, that run in min(2 f +4; 2t +1) and

3min(f +2; t + 1) rounds, are presented in [24]and[5],

respectively. In these algorithms the number of sent mes-

sages is O(n

), moreover, in the latter algorithm the mes-

sages are of constant size (2 bits). Both algorithms assume

V = f0; 1g. To solve the BA problem for a larger V, sev-

eral instances of a binary algorithm can be run in paral-

lel. Alternatively, there exists a simple 2-round protocol

that reduces a BA problem with arbitrary initial values to

the binary case, e. g., see Sect. 6.3.3 in [19]. For algorithms

with optimal O(nt) message complexity and t + o(t)round

complexity see [4,9].

Arbitrary Network Topologies

When the network is not fully connected, BA can be solved

for crash, omission and authenticated Byzantine failures if

and only if it is (t + 1)-connected [12]. In case of Byzantine

failures without authentication, BA has a solution if and

only if the network is (2t + 1)-connected and n > 3t [19].

In both cases the BA problem can be solved by simulat-

ing the algorithms for the fully connected network, using

the fact that the number of disjoint communication paths

between any pair of non-adjacent processors exceeds the

number of faulty nodes by an amount that is suﬃcient for

reliable communication.

Interactive Consistency and Byzantine Generals

The BA (consensus) problem can be stated in several simi-

lar ways. Two widely used variants are the Byzantine Gen-

erals (BG) problem and the Interactive Consistency (IC)

problem. In the BG case there is a designated processor,

say p

, which is the only one to have an input value. The

termination and agreement requirements of the BG prob-

lem are exactly as in BA, while the validity condition re-

quires that if the input value of p

is v and p

is correct,

then the correct processors decide v.TheICproblemis

an extension of BG, where every processor is “designated”,

so that each processor has to decide on a vector of n val-

ues, where the conditions for the i-th entry are as in BG,

with p

as the designated processor. For deterministic syn-

chronous algorithms BA, BG and IC problems are essen-

tially equivalent, e. g., see the discussion in [15].

Firing Squad

The above algorithms assume that the processors share

a “global time”, i. e., all the processors start in the same

(ﬁrst) round, so that their round counters are equal

throughout the execution of the algorithm. However, there

are cases in which the processors run in a synchronous

network, yet each processor has its own notion of time

(e. g., when each processor starts on its own, the round

counter values are distinct among the processors). In these

cases, it is desirable to have a protocol that allows the

processors to agree on some speciﬁc round, thus creating

a common round which synchronizes all the correct pro-

cessors. This synchronization task, known as the Byzan-

tine ﬁring squad problem [6], is tightly realted to BA.

General Translation Techniques

One particular direction that was pursued as part of the

research on the BA problem is the development of meth-

ods that automatically translate any protocol that tolerates

a more benign failure type into one which tolerates more

severe failures [24]. Eﬃcient translations spanning the en-

tire failure hierarchy, starting from crash failures all the

way to unauthenticated Byzantine failures, can be found

in [3]andinCh.12of[1].

Applications

Due to the very tight synchronization assumptions made

in the algorithms presented above, they are used mainly in

real-time, safety-critical systems, e. g., aircraft control [13].

In fact, the original interest of Pease, Shostak and Lamport

in this problem was raised by such an application [21]. In

Byzantine Agreement B 119

addition, BA protocols for the Byzantine failure case serve

as a basic building block in many cryptographic proto-

cols, e. g., secure multi-party computation [17], by provid-

ing a broadcast channel on top of pairwise communication

channels.

Cross References

 Asynchronous Consensus Impossibility

 Atomic Broadcast

 Consensus with Partial Synchrony

 Failure Detectors

 Optimal Probabilistic Synchronous Byzantine

Agreement

 Randomization in Distributed Computing

 Renaming

 Set Agreement

Recommended Reading

1. Attiya, H., Welch, J.L.: Distributed Computing: Fundamentals,

Simulations and Advanced Topics. McGraw-Hill, UK (1998)

2. Barborak, M., Dahbura, A., Malek, M.: The Consensus Prob-

lem in Fault-Tolerant Computing. ACM Comput. Surv. 25(2),

171–220 (1993)

3. Bazzi, R.A., Neiger, G.: Simplifying Fault-tolerance: Providing

the Abstraction of Crash Failures. J. ACM 48(3), 499–554 (2001)

4. Berman, P., Garay, J.A., Perry, K.J.: Bit Optimal Distributed Con-

sensus. In: Yaeza-Bates, R., Manber, U. (eds.) Computer Science

Research, pp. 313–322. Plenum Publishing Corporation, New

York (1992)

5. Berman, P., Garay, J.A., Perry, K.J.: Optimal Early Stopping in

Distributed Consensus. In: Proc. 6th International Workshop on

Distributed Algorithms (WDAG), pp. 221–237, Israel, Novem-

ber 1992

6. Burns, J.E., Lynch, N.A.: The Byzantine Firing Squad problem.

Adv. Comput. Res. 4, 147–161 (1987)

7. Charron-Bost, B., Schiper, A.: Uniform Consensus is Harder than

Consensus. J. Algorithms 51(1), 15–37 (2004)

8. Chlebus, B.S., Kowalski, D.R.: Time and Communication

Efficient Consensus for Crash Failures. In: Proc. 20th Inter-

national Symposium on Distributed Computing (DISC),

pp. 314–328, Sweden, September 2006

9. Coan, B.A., Welch, J.L.: Modular construction of a Byzantine

agreement protocol with optimal message bit complexity. Inf.

Comput. 97(1), 61–85 (1992)

10. Dolev, D., Reischuk, R.: Bounds on Information Exchange for

Byzantine Agreement. J. ACM 32(1), 191–204 (1985)

11. Dolev,D.,Reischuk,R.,Strong,H.R.:EarlyStoppinginByzantine

Agreement. J. ACM 37(4), 720–741 (1990)

12. Dolev, D., Strong, H.R.: Authenticated Algorithms for Byzantine

Agreement. SIAM J. Comput. 12(4), 656–666 (1983)

13. Driscoll, K., Hall, B., Sivencrona, H., Zumsteg, P.: Byzantine

Fault Tolerance, from Theory to Reality. In: Proc. 22nd Interna-

tional Conference on Computer Safety, Reliability, and Security

(SAFECOMP), pp. 235–248, UK, September 2003

14. Dwork, C., Moses, Y.: Knowledge and Common Knowledge in

a Byzantine Environment: Crash Failures. Inf. Comput. 88(2),

156–186 (1990)

15. Fischer, M.J.: The Consensus Problem in Unreliable Distributed

Systems (A Brief Survey). Research Report, YALEU/DCS/RR-273,

Yale University, New Heaven (1983)

16. Garay, J.A., Moses, Y.: Fully Polynomial Byzantine Agreement

for n > 3t Processors in t + 1 Rounds. SIAM J. Comput. 27(1),

247–290 (1998)

17. Goldreich, O.: Foundations of Cryptography, vol. 1-2. Cam-

bridge University Press, UK (2001) (2004)

18. Lamport,L.,Shostak,R.E.,Pease,M.C.:TheByzantineGenerals

Problem. ACM Trans. Program. Lang. Syst. 4(3), 382–401 (1982)

19. Lynch, N.A.: Distributed Algorithms. Morgan Kaufmann, CA

(1996)

20. Parvédy, P.R., Raynal, M.: Optimal Early Stopping Uniform Con-

sensus in Synchronous Systems with Process Omission Fail-

ures. In: Proc. 16th Annual ACM Symposium on Parallel Algo-

rithms (SPAA), pp. 302–310, Spain, June 2004

21. Pease, M.C., Shostak, R.E., Lamport, L.: Reaching Agreement in

thePresenceofFaults.J.ACM27(2), 228–234 (1980)

22. Perry, K.J., Toueg, S.: Distributed Agreement in the Presence of

Processor and Communication Faults. IEEE Trans. Softw. Eng.

12(3), 477–482 (1986)

23. Raynal, M.: Consensus in Synchronous Systems: A Concise

Guided Tour. In: Proc. 9th Pacific Rim International Symposium

on Dependable Computing (PRDC), pp. 221–228, Japan, De-

cember 2002

24. Toueg, S., Perry, K.J., Srikanth,T.K.: Fast Distributed Agreement.

SIAM J. Comput. 16(3), 445–457 (1987)

Cache-Oblivious B-Tree C 121

Cache-Oblivious B-Tree

2005; Bender, Demaine, Farach-Colton

ROLF FAGERBERG

Department of Mathematics and Computer Science,

University of Southern Denmark,

Odense, Denmark

Keywords and Synonyms

Cache-oblivious search tree; Cache-oblivious dictionary

Problem Definition

Computers contain a hierarchy of memory levels, with

vastly diﬀering access times. Hence, the time for a mem-

ory access depends strongly on what is the innermost level

containing the data accessed. In analysis of algorithms, the

standard RAM (or von Neumann) model cannot capture

this eﬀect, and external memory models were introduced

to better model the situation. The most widely used of

these models is the two-level I/O-model [1], also called the

External Memory model or the Disk Access model. The

I/O-model approximates the memory hierarchy by mod-

eling two levels, with the inner level having size M,the

outer level having inﬁnite size, and transfers between the

levels taking place in blocks of B consecutive elements. The

cost of an algorithm is the number of memory transfers it

makes.

The cache-oblivious model, introduced by Frigo

et al. [18], elegantly generalizes the I/O-model to a multi-

level memory model by a simple measure: the algorithm is

not allowed to know the value of B and M.Moreprecisely,

a cache-oblivious algorithm is an algorithm formulated in

the RAM model, but analyzed in the I/O-model, with an

analysis valid for any value of B and M. Cache replace-

ment is assumed to take place automatically by an opti-

mal oﬀ-line cache replacement strategy. Since the analysis

holds for any B and M, it holds for all levels simultane-

ously.

The subject here is that of eﬃcient cache-oblivious

data structures for the ordered dictionary problem, i. e.,

the problem of storing elements with keys from an ordered

universe while supporting searches, insertions, deletions,

and range searches. In full generality, searches are prede-

cessor searches, returning the element with the largest key

smaller than or equal to the key searched for.

Key Results

The ﬁrst cache-oblivious dictionary was given by Pro-

kop [21], who showed how to lay out a static binary

tree in memory such that searches take O(log

n)mem-

ory transfers. This layout, often called the van Emde Boas

layout because it is reminiscent of the classic van Emde

Boas data structure, also ensures that range searches take

O(log

n + k/B) memory transfers [2], where k is the size

of the output. Both bounds are optimal for comparison-

based searching.

The ﬁrst dynamic, cache-oblivious dictionary was

given by Bender et al. [10].Makinguseofavariantofthe

van Emde Boas layout, a density maintenance algorithm of

the type invented by Itai et al. [19], and weight-balanced

B-trees [5], they arrived at the following results:

Theorem 1 ([10]) There is a cache-oblivious dictionary

structure supporting searches in O(log

n) memory trans-

fers, and insertions and deletions in amortized O(log

memory transfers.

Theorem 2 ([10]) There is a cache-oblivious dictionary

structure supporting searches in O(log

n) memory trans-

fers, insertions and deletions in amortized O(log

n +

(log

n)/B) memory transfers, and range searches in

O(log

n + k/B) memory transfers, where k is the size of

the output.

Later, Bender et al. [7] developed a cache-oblivious struc-

ture for maintaining linked lists which supports inser-

tion and deletion of elements in O(1) memory trans-

122 C Cache-Oblivious B-Tree

fers and scanning of k consecutive elements in amortized

O(k/B) memory transfers. Combining this structure with

the structure of the ﬁrst theorem above, the following re-

sult can be achieved.

Theorem 3 ([7,10]) There is a cache-oblivious dictio-

nary structure supporting searches in O(log

n) memory

transfers, insertions and deletions in amortized O(log

memory transfers, and range searches in amortized

O(log

n + k/B) memory transfers, where k is the size of the

output.

A long list of extensions of these basic cache-oblivious dic-

tionary results has been given. We now survey these.

Bender et al. [11] and Brodal et al. [16] gave very sim-

ilar proposals for reproducing the result of Theorem 2,

but with signiﬁcantly simpler structures (avoiding the use

of weight-balanced B-trees). On the basis of exponen-

tial trees, Bender et al.[8] gave a proposal with O(log

worst-case queries and updates. They also gave a solu-

tion with partial persistence, where searches (in all ver-

sions of the structure) and updates (in the latest version of

the structure) require amortized O(log

(m + n)) memory

transfers, where m is the number of versions and n is the

number of elements in the version operated on. Bender et

al. [14] extended the cache-oblivious model to a concur-

rent setting, and gave three proposals for cache-oblivious

B-trees in this setting. Bender et al. [12] gave cache-obliv-

ious dictionary structures exploring trade-oﬀs between

faster insertion costs and slower search cost. Franceschini

and Grossi [17] showed how to achieve O(log

n)worst-

case queries and updates while using O(1) space besides

the space for the n elements stored. Extensions to dictio-

naries on other data types such as strings [13,15]andgeo-

metric data [3,4,6] have been given.

It has been shown [9] that the best-possible multiplica-

tive constant in the (log

n) search bound for compari-

son-based searching is diﬀerent in the I/O-model and in

the cache-oblivious model.

Applications

Dictionaries solve a fundamental data structuring prob-

lem which is part of solutions for a very high number of

computational problems. Dictionaries for external mem-

ory are useful in settings where memory accesses are dom-

inating the running time, and cache-oblivious dictionaries

in particular stand out by their ability to optimize the ac-

cess to all levels of an unknown memory hierarchy. This is

an asset e. g. when developing programs to be run on di-

verse or unknown architectures (such as software libraries

or programs for heterogeneous distributed computing like

grid computing and projects such as SETI@home). Even

on a single, known architecture, the memory parameters

available to a computational process may be non-con-

stant if several processes compete for the same memory

resources. Since cache-oblivious algorithms are optimized

for all parameter values, they have the potential to adapt

more gracefully to these changes, and also to varying in-

put sizes forcing diﬀerent memory levels to be in use.

Open Problems

For the one-dimensional ordered dictionary problem dis-

cussed here, one notable open problem is to ﬁnd a data

structure achieving worst case versions of all the bounds

in Theorem 3.

Experimental Results

Cache-oblivious dictionaries have been evaluated empir-

ically in [11,13,16,20,22]. The overall conclusion of these

investigations is that cache-oblivious methods easily can

outperform RAM algorithms, although sometimes not as

much as algorithms tuned to the speciﬁc memory hier-

archy and problem size in question. On the other hand,

cache-oblivious algorithms seem to perform well on all

levels of the memory hierarchy, and to be more robust to

changing problem sizes.

Cross References

 B-trees

 Cache-Oblivious Model

 Cache-Oblivious Sorting

 I/O-model

Recommended Reading

1. Aggarwal, A., Vitter, J.S.: The Input/Output complexity of sort-

ing and related problems. Commun. ACM 31(9), 1116–1127

(1988)

2. Arge, L., Brodal, G.S., Fagerberg, R.: Cache-oblivious data struc-

tures.In:Mehta,D.,Sahni,S.(eds.)HandbookonDataStruc-

tures and Applications. CRC Press, Boca Raton (2005)

3. Arge, L., Brodal, G.S., Fagerberg, R., Laustsen, M.: Cache-oblivi-

ous planar orthogonal range searching and counting. In: Proc.

21st ACM Symposium on Computational Geometry, pp. 160–

169. ACM, New York (2005)

4. Arge,L.,deBerg,M.,Haverkort,H.J.:Cache-obliviousR-trees.

In: Proc. 21st ACM Symposium on Computational Geometry,

pp. 170–179. ACM, New York (2005)

5. Arge, L., Vitter, J.S.: Optimal external memory interval manage-

ment. SIAM J. Comput. 32(6), 1488–1508 (2003)

6. Arge, L., Zeh, N.: Simple and semi-dynamic structures for

cache-oblivious planar orthogonal range searching. In: Proc.

22nd ACM Symposium on Computational Geometry, pp. 158–

166. ACM, New York (2006)

Cache-Oblivious Model C 123

7. Bender, M., Cole, R., Demaine, E., Farach-Colton, M.: Scan-

ning and traversing: Maintaining data for traversals in a mem-

ory hierarchy. In: Proc. 10th Annual European Symposium

on Algorithms. LNCS, vol. 2461, pp. 139–151. Springer, Berlin

(2002)

8. Bender, M., Cole, R., Raman, R.: Exponential structures for

cache-oblivious algorithms. In: Proc. 29th International Col-

loquium on Automata, Languages, and Programming. LNCS,

vol. 2380, pp. 195–207. Springer, Berlin (2002)

9. Bender, M.A., Brodal, G.S., Fagerberg, R., Ge, D., He, S., Hu, H.,

Iacono, J., Lopez-Ortiz, A.: The cost of cache-oblivious search-

ing. In: Proc. 44th Annual IEEE Symposium on Foundations of

Computer Science, pp. 271–282. IEEE Computer Society Press,

Los Alamitos (2003)

10. Bender, M.A., Demaine, E.D., Farach-Colton, M.: Cache-oblivi-

ous B-trees. SIAM J. Comput. 35(2), 341–358 (2005). Confer-

ence version appeared at FOCS (2000)

11. Bender, M.A., Duan, Z., Iacono, J., Wu, J.: A locality-preserving

cache-oblivious dynamic dictionary. J. Algorithms 53(2), 115–

136 (2004). Conference version appeared at SODA (2002)

12. Bender, M.A., Farach-Colton, M., Fineman, J.T., Fogel, Y.R., Kusz-

maul, B.C., Nelson, J.: Cache-oblivious streaming B-trees. In:

Proc. 19th Annual ACM Symposium on Parallel Algorithms and

Architectures, pp. 81–92. ACM, New York (2007)

13. Bender, M.A., Farach-Colton, M., Kuszmaul, B.C.: Cache-oblivi-

ous string B-trees. In: Proc. 25th ACM SIGACT-SIGMOD-SIGART

Symposium on Principles of Database Systems, pp. 233–242.

ACM, New York (2006)

14. Bender, M.A., Fineman, J.T., Gilbert, S., Kuszmaul, B.C.: Concur-

rent cache-oblivious B-trees. In: Proc. 17th Annual ACM Sym-

posium on Parallel Algorithms, pp. 228–237. ACM, New York

(2005)

15. Brodal, G.S., Fagerberg, R.: Cache-oblivious string dictionar-

ies. In: SODA: ACM-SIAM Symposium on Discrete Algorithms,

pp. 581–590. ACM Press, New York (2006)

16. Brodal, G.S., Fagerberg, R., Jacob, R.: Cache-oblivious search

trees via binary trees of small height. In: Proc. 13th Annual

ACM-SIAM Symposium on Discrete Algorithms, pp. 39–48

ACM, New York (2002)

17. Franceschini, G., Grossi, R.: Optimal worst-case operations for

implicit cache-oblivious search trees. In: Proc. Algorithms and

Data Structures, 8th International Workshop, WADS. LNCS,

vol. 2748, pp. 114–126. Springer, Berlin (2003)

18. Frigo, M., Leiserson, C.E., Prokop, H., Ramachandran, S.: Cache-

oblivious algorithms. In: 40th Annual IEEE Symposium on

Foundations of Computer Science, pp. 285–298. IEEE Com-

puter Society Press, Los Alamitos (1999)

19. Itai, A., Konheim, A.G., Rodeh, M.: A sparse table implementa-

tion of priority queues. In: Automata, Languages and Program-

ming, 8th Colloquium. LNCS, vol. 115, pp. 417–431. Springer,

Berlin (1981)

20. Ladner, R.E., Fortna, R., B.-Nguyen, H.: A comparison of cache

aware and cache oblivious static search trees using pro-

gram instrumentation. In: Experimental Algorithmics. LNCS,

vol. 2547, pp. 78–92. Springer, Berlin (2000)

21. Prokop, H.: Cache-oblivious algorithms. Master’s thesis, Mas-

sachusetts Institute of Technology (1999)

22. Rahman, N., Cole, R., Raman, R.: Optimised predecessor data

structures for internal memory. In: Proc. Algorithm Engineer-

ing, 5th International Workshop, WAE. LNCS, vol. 2141, pp. 67–

78. Springer, Berlin (2001)

Cache-Oblivious Model

1999; Frigo, Leiserson, Prokop, Ramachandran

ROLF FAGERBERG

Department of Mathematics and Computer Science,

University of Southern Denmark, Odense, Denmark

Model Definition

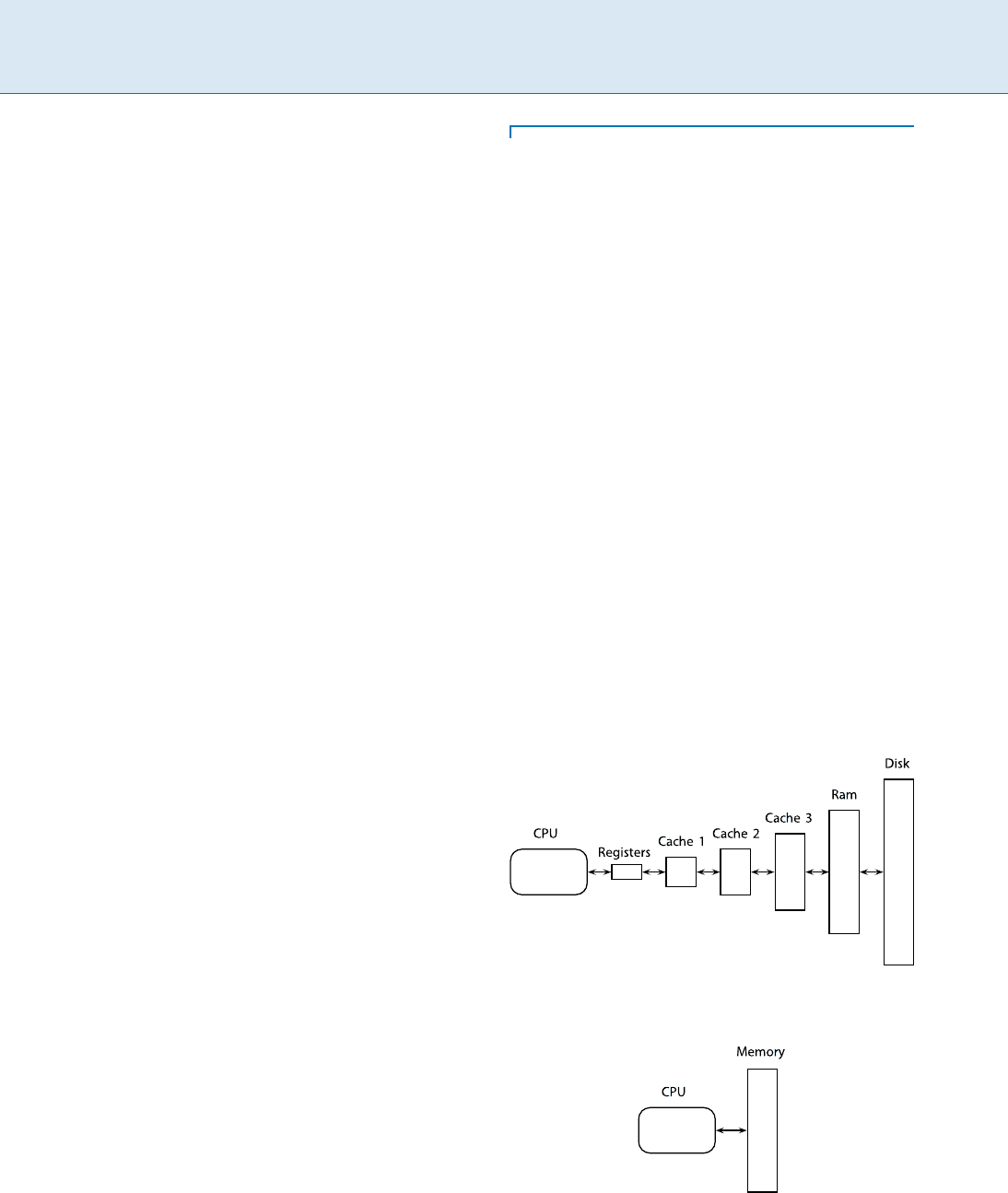
The memory system of contemporary computers consists

of a hierarchy of memory levels, with each level acting as

a cache for the next; a typical hierarchy may consist of

registers, level 1 cache, level 2 cache, level 3 cache, main

memory, and disk (Fig. 1). One characteristic of the hier-

archy is that the memory levels get larger and slower the

further they get from the processor, with the access time

increasing most dramatically between RAM memory and

disk. Another characteristic is that data is moved between

levels in blocks.

As a consequence of the diﬀerences in access time be-

tween the levels, the cost of a memory access depends

highly on what is the current lowest memory level hold-

ing the element accessed. Hence, the memory access pat-

tern of an algorithm has a major inﬂuence on its practi-

cal running time. Unfortunately, the RAM model (Fig. 2)

traditionally used to design and analyze algorithms is not

Cache-Oblivious Model, Figure 1

The memory hierarchy

Cache-Oblivious Model, Figure 2

The RAM model

124 C Cache-Oblivious Model

Cache-Oblivious Model, Figure 3

The I /O-model

capable of capturing this, as it assumes that all memory ac-

cesses take equal time.

To better account for the eﬀects of the memory hier-

archy, a number of computational models have been pro-

posed. The simplest and most successful is the two-level

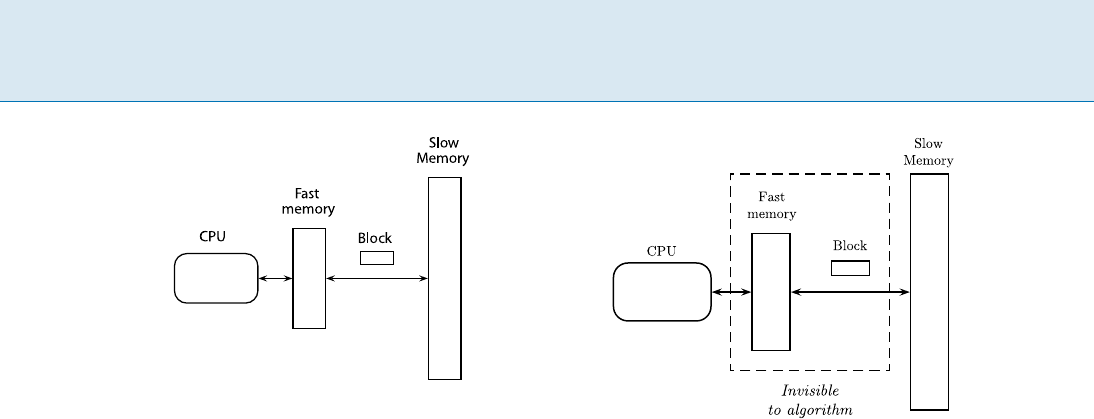
I/O-model introduced by Aggarwal and Vitter [2](Fig.3).

In this model a two-level memory hierarchy is assumed,

consisting of a fast memory of size M and a slower mem-

ory of inﬁnite size, with data transferred between the lev-

els in blocks of B consecutive elements. Computation can

only be performed on data in the fast memory, and algo-

rithms are assumed to have complete control over trans-

fers of blocks between the two levels. Such a block trans-

fer is denoted a memory transfer. The complexity mea-

sure is the number of memory transfers performed. The

strength of the I/O-model is that it captures part of the

memory hierarchy, while being suﬃciently simple to make

design and analysis of algorithms feasible. Over the last

two decades, a large body of results for the I/O-model has

been produced, covering most areas of algorithmics. For

an overview, see the surveys [3,24,26,27].

More elaborate models of multi-level memory have

been proposed (see e. g. [26] for an overview) but these

models have been less successful than the I/O-model,

mainly because of their complexity which makes analy-

sis of algorithms harder. All these models, including the

I/O-model, assume that the characteristics of the memory

hierarchy (the level and block sizes) are known.

In 1999 the cache-oblivious model (Fig. 4)wasintro-

duced by Frigo et al. [22]. A cache-oblivious algorithm is

an algorithm formulated in the RAM model but analyzed

in the I/O-model, with the analysis required to hold for

any block size B and memory size M. Memory transfers

are assumed to take place automatically by an optimal oﬀ-

line cache replacement strategy.

The crux of the cache-oblivious model is that because

the I/O-model analysis holds for any block and memory

Cache-Oblivious Model, Figure 4

The cache-oblivious model

size, it holds for all levels of a multi-level memory hier-

archy (see [22,25] for detailed versions of this statement).

Put diﬀerently, by optimizing an algorithm to one un-

known level of the memory hierarchy, it is optimized to all

levels simultaneously. Thus, the cache-oblivious model el-

egantly generalizes the I/O-model to a multi-levelmemory

model by one simple measure: the algorithm is not allowed

to know the value of B and M. The challenge, of course, is

to develop algorithms having good memory transfer ana-

lyzes under these conditions.

Besides capturing the entire memory hierarchy in

a conceptually simple way, the cache-oblivious model has

other beneﬁts: Algorithms developed in the model do not

rely on knowing the parameters of the memory hierarchy,

which is an asset when developing programs to be run on

diverse or unknown architectures (e. g. software libraries

or programs for heterogeneous distributed computing

such as grid computing and projects like SETI@home).

Even on a single, known architecture, the memory param-

eters available to a computational process may be non-

constant if several processes compete for the same mem-

ory resources. Since cache-oblivious algorithms are opti-

mized for all parameter values, they have the potential to

adapt more gracefully to these changes. Also, the same

code will adapt to varying input sizes forcing diﬀerent

memory levels to be in use. Finally, cache-oblivious algo-

rithms automatically are optimizing the use of translation

lookaside buﬀers (a cache holding recently accessed parts

of the page table used for virtual memory) of the CPU,

which may be seen as a second memory hierarchy paral-

lel to the one mentioned in the introduction.

Possible weak points of the cache-oblivious model are

the assumption of optimal oﬀ-line cache replacement, and

the lack of modeling of the limited associativity of many of

the levels of the hierarchy. The ﬁrst point is mitigated by

Cache-Oblivious Model C 125

the fact that normally, the provided analysis of a proposed

cache-oblivious algorithm will work just as well assuming

a Least-Recently-Used cache replacement policy, which is

closer to actual replacement strategies of computers. The

second point is also a weak point of most other memory

models.

Key Results

This section surveys a number of the known results in

the cache-oblivious model. Other surveys available in-

clude [5,14,20,24].

First of all, note that scanning an array of N elements

takes O(N/B) memory transfers for any values of B and M,

and hence is an optimal cache-oblivious algorithm. Thus,

standard RAM algorithms based on scanning may already

possess good analysis in the cache-oblivious model – for

instance, the classic deterministic selection algorithm has

complexity O(N/B)[20].

For sorting, a fundamental fact in the I/O-model is that

comparison-based sorting of N elements takes (Sort(N))

memory transfers [2], where Sort(N)=

log

M/B

.Also

in the cache-oblivious model, sorting can be carried out in

(Sort(N)) memory transfer, if one makes the so-called

tall cache assumption M  B

1+"

[15,22]. Such an assump-

tion has been shown to be necessary [16], which proves

a separation in power between cache-oblivious algorithms

and algorithms in the I/O-model (where this assumption

is not needed for the sorting bound).

For searching, B-trees have cost O(log

N), which is

optimal in the I/O-model for comparison-based searching.

This cost is also attainable in the cache-oblivious model,

as shown for the static case in [25] and for the dynamic

case in [13]. A number of later variants of cache-oblivious

search trees have appeared. Also for searching, a separa-

tion between cache-oblivious algorithms and algorithms

in the I/O-model has been shown [12] in the sense that the

constants attainable in the O(log

N)boundareprovably

diﬀerent.

Permuting in the I/O-model has complexity (minf

Sort(N); Ng), assuming that elements are indivisible [2]. It

has been proven [16] that this asymptotic complexity can-

not be attained in the cache-oblivious model, hence also

for this problem, a separation exists.

Cache-oblivious priority queues supporting opera-

tions in O(1/B log

M/B

N/M) memory transfers amortized

have been given.

Currently known cache-oblivious algorithms also in-

clude algorithms for problems in computational geom-

etry [1,6,7,8,10,15], for graph problems [4,17,18,23], for

scanning dynamic sets [9], for layout of static trees [11],

for search problems on multi-sets [21], for dynamic pro-

gramming [19], for partial persistence [10], for matrix op-

erations [22], and for the Fast Fourier Transform [22].

Applications

The cache-oblivious model is a means for design and anal-

ysis of algorithms that use the memory hierarchy of com-

puters eﬃciently.

Experimental Resul t s

Cache-oblivious algorithms have been evaluated empiri-

cally in a number of areas, including sorting, searching,

matrix algorithms [22], and dynamic programming [19].

The overall conclusion of these investigations is that

cache-oblivious methods often outperform RAM algo-

rithms, but not always exactly as much as do algorithms

tuned to the speciﬁc memory hierarchy and problem size.

On the other hand, cache-oblivious algorithms seem to

perform well on all levels of the memory hierarchy, and

to be more robust to changing problem sizes.

Cross References

 Cache-Oblivious B-Tree

 Cache-Oblivious Sorting

 I/O-model

Recommended Reading

1. Agarwal, P.K., Arge, L., Danner, A., Holland-Minkley, B.: Cache-

oblivious data structures for orthogonal range searching. In:

Proc. 19th ACM Symposium on Computational Geometry,

pp. 237–245. ACM, New York (2003)

2. Aggarwal, A., Vitter, J.S.: The Input/Output complexity of sort-

ing and related problems. Commun. ACM 31(9), 1116–1127

(1988)

3. Arge, L.: External memory data structures. In: Abello, J., Parda-

los, P.M., Resende, M.G.C. (eds.) Handbook of Massive Data

Sets, pp. 313–358. Kluwer Academic Publishers, Boston (2002)

4. Arge, L., Bender, M.A., Demaine, E.D., Holland-Minkley, B.,

Munro, J.I.: Cache-oblivious priority queue and graph algo-

rithm applications. In: Proc. 34th Annual ACM Symposium on

Theory of Computing, pp. 268–276. ACM, New York (2002)

5. Arge, L., Brodal, G.S., Fagerberg, R.: Cache-oblivious data struc-

tures. In: Mehta, D., Sahni, S. (eds.) Handbook on Data Struc-

tures and Applications. CRC Press, Boca Raton (2005)

6. Arge, L., Brodal, G.S., Fagerberg, R., Laustsen, M.: Cache-oblivi-

ous planar orthogonal range searching and counting. In: Proc.

21st Annual ACM Symposium on Computational Geometry,

pp. 160–169. ACM, New York (2005)

7. Arge,L.,deBerg,M.,Haverkort,H.J.:Cache-obliviousR-trees.In:

Symposium on Computational Geometry, pp. 170–179. ACM,

New York (2005)

126 C Cache-Oblivious Sorting

8. Arge, L., Zeh, N.: Simple and semi-dynamic structures for

cache-oblivious planar orthogonal range searching. In: Sym-

posium on Computational Geometry, pp. 158–166. ACM, New

York (2006)

9. Bender, M., Cole, R., Demaine, E., Farach-Colton, M.: Scan-

ning and traversing: Maintaining data for traversals in a mem-

ory hierarchy. In: Proc. 10th Annual European Symposium

on Algorithms. LNCS, vol. 2461, pp. 139–151. Springer, Berlin

(2002)

10. Bender, M., Cole, R., Raman, R.: Exponential structures for

cache-oblivious algorithms. In: Proc. 29th International Col-

loquium on Automata, Languages, and Programming. LNCS,

vol. 2380, pp. 195–207. Springer, Berlin (2002)

11. Bender, M., Demaine, E., Farach-Colton, M.: Efficient tree layout

in a multilevel memory hierarchy. In: Proc. 10th Annual Euro-

pean Symposium on Algorithms. LNCS, vol. 2461, pp. 165–173.

Springer, Berlin (2002). Full version at http://arxiv.org/abs/cs/

0211010

12. Bender, M.A., Brodal, G.S., Fagerberg, R., Ge, D., He, S., Hu, H.,

Iacono, J., López-Ortiz, A.: The cost of cache-oblivious search-

ing. In: Proc. 44th Annual IEEE Symposium on Foundations of

Computer Science, pp. 271–282. IEEE Computer Society Press,

Los Alamitos (2003)

13. Bender, M.A., Demaine, E.D., Farach-Colton, M.: Cache-obliv-

ious B-trees. In: 41st Annual Symposium on Foundations of

Computer Science, pp. 399–409. IEEE Computer Society Press,

Los Alamitos (2000)

14. Brodal, G.S.: Cache-oblivious algorithms and data structures.

In: Proc. 9th Scandinavian Workshop on Algorithm Theory.

LNCS, vol. 3111, pp. 3–13. Springer, Berlin (2004)

15. Brodal, G.S., Fagerberg, R.: Cache oblivious distribution sweep-

ing. In: Proc. 29th International Colloquium on Automata,

Languages, and Programming. LNCS, vol. 2380, pp. 426–438.

Springer, Berlin (2002)

16. Brodal, G.S., Fagerberg, R.: On the limits of cache-oblivious-

ness. In: Proc. 35th Annual ACM Symposium on Theory of Com-

puting, pp. 307–315. ACM, New York (2003)

17. Brodal, G.S., Fagerberg, R., Meyer, U., Zeh, N.: Cache-oblivi-

ous data structures and algorithms for undirected breadth-

first search and shortest paths. In: Proc. 9th Scandinavian

Workshop on Algorithm Theory. LNCS, vol. 3111, pp. 480–492.

Springer, Berlin (2004)

18. Chowdhury, R.A., Ramachandran, V.: Cache-oblivious shortest

paths in graphs using buffer heap. In: Proc. 16th Annual ACM

Symposium on Parallelism in Algorithms and Architectures.

ACM, New York (2004)

19. Chowdhury, R.A., Ramachandran, V.: Cache-oblivious dynamic

programming. In: Proc. 17th Annual ACM-SIAM Symposium on

Discrete Algorithms, pp. 591–600. ACM-SIAM, New York (2006)

20. Demaine, E.D.: Cache-oblivious algorithms and data struc-

tures. In: Proc. EFF summer school on massive data sets, LNCS.

Springer, Berlin. To appear. Online version at http://theory.

csail.mit.edu/edemaine/papers/BRICS2002/

21. Farzan, A., Ferragina, P., Franceschini, G., Munro, J.I.: Cache-

oblivious comparison-based algorithms on multisets. In: Proc.

13th Annual European Symposium on Algorithms. LNCS,

vol. 3669, pp. 305–316. Springer, Berlin (2005)

22. Frigo, M., Leiserson, C.E., Prokop, H., Ramachandran, S.: Cache

oblivious algorithms. In: 40th Annual IEEE Symposium on

Foundations of Computer Science, pp. 285–298. IEEE Com-

puter Society Press, Los Alamitos (1999)

23. Jampala, H., Zeh, N.: Cache-oblivious planar shortest paths. In:

Proc. 32nd International Colloquium on Automata, Languages,

and Programming. LNCS, vol. 3580, pp. 563–575. Springer,

Berlin (2005)

24. Meyer,U.,Sanders,P.,Sibeyn,J.F.(eds.):AlgorithmsforMem-

ory Hierarchies. LNCS, vol. 2625. Springer, Berlin (2003)

25. Prokop, H.: Cache-oblivious algorithms. Master’s thesis, Mas-

sachusetts Institute of Technology, Dept. of Electrical Engi-

neering and Computer Science (1999)

26. Vitter, J.S.: External memory algorithms and data structures:

Dealing with MASSIVE data. ACM Comput. Surv. 33(2), 209–

271 (2001)

27. Vitter, J.S.: Geometric and spatial data structures in external

memory. In: Mehta, D., Sahni, S. (eds.) Handbook on Data Struc-

tures and Applications. CRC Press, Boca Raton (2005)

Cache-Oblivious Sorting

1999; Frigo, Leiserson, Prokop, Ramachandran

GERTH STØLTING BRODAL

Department of Computer Science, University of Aarhus,

Århus, Denmark

Keywords and Synonyms

Funnel sort

Problem Definition

Sorting a set of elements is one of the most well-studied

computational problems. In the cache-oblivious setting

the ﬁrst study of sorting was presented in 1999 in the sem-

inal paper by Frigo et al. [8] that introduced the cache-

oblivious framework for developing algorithms aimed at

machines with (unknown) hierarchical memory.

Model

In the cache-oblivious setting the computational model

is a machine with two levels of memory: a cache of lim-

ited capacity and a secondary memory of inﬁnite capac-

ity. The capacity of the cache is assumed to be M elements

and data is moved between the two levels of memory in

blocks of B consecutive elements. Computations can only

be performed on elements stored in cache, i. e. elements

from secondary memory need to be moved to the cache

before operations can access the elements. Programs are

written as acting directly on one unbounded memory, i. e.

programs are like standard RAM programs. The necessary

block transfers between cache and secondary memory are

handled automatically by the model, assuming an optimal

oﬄine cache replacement strategy. The core assumption of

the cache-oblivious model is that M and B are unknown to

Cache-Oblivious Sorting C 127

the algorithm whereas in the related I/O model introduced

by Aggarwal and Vitter [1] the algorithms know M and

B and the algorithms perform the block transfers explic-

itly. A thorough discussion of the cache-oblivious model

and its relation to multi-level memory hierarchies is given

in [8].

Sorting

For the sorting problem the input is an array of N elements

residing in secondary memory, and the output is required

to be an array in secondary memory storing the input ele-

ments in sorted order.

Key Results

IntheI/Omodeltightupperandlowerboundswere

proved for the sorting problem and the problem of

permuting an array [1]. In particular it was proved

that sorting requires (

log

M/B

)blocktransfersand

permuting an array requires (minfN;

log

M/B

block transfers. Since lower bounds for the I/O model

also hold for the cache-oblivious model, the lower

bounds from [1] immediately give a lower bound of

˝(

log

M/B

) block transfers for cache-oblivious sort-

ing and ˝(minfN;

log

M/B

g)blocktransfersfor

cache-oblivious permuting. The upper bounds from [1]

can not be applied to the cache-oblivious setting since

thesealgorithmsmakeexplicituseofB and M.

Binary Mergesort performs O(N log

N)comparisons,

but analyzed in the cache-oblivious model it performs

log

) block transfers which is a factor (log

)

from the lower bound (assuming a recursive implemen-

tation of binary Mergesort, in order to get M in the de-

nominator in the log N/M part of the bound on the block

transfers). Another comparison-based sorting algorithm

is the classical Quicksort sorting algorithm from 1962

by Hoare [9], that performs expected O(N log

N)com-

parisons and expected O(

log

) block transfers. Both

these algorithms achieve their relatively good performance

for the number of block transfers from the fact that they

are based on repeated scanning of arrays—a property not

shared with e. g. Heapsort [10] that has a very poor perfor-

mance of (N log

) block transfers. In the I/O model

the optimal performance of O(

log

M/B

) is achieved

by generalizing binary Mergesort to (

)-way Merge-

sort [1].

Frigo et al. in [8] presented two cache-oblivious sort-

ing algorithms (which can also be used to permute an ar-

ray of elements). The ﬁrst algorithm [8,Section4]isde-

noted Funnelsort and is a reminiscent of classical binary

Mergesort, whereas the second algorithm [8,Section5]

is a distribution-based sorting algorithm. Both algorithms

perform optimal O(

log

M/B

)blocktransfers–pro-

vided a tall cache assumption M = ˝(B

)issatisﬁed.

Funnelsort

The basic idea of Funnelsort is to rearrange the sorting

process performed by binary Mergesort, such that the pro-

cessed data is stored “locally.” This is achieved by two ba-

sic ideas: (1) A top-level recursion that partitions the in-

put into N

1/3

sequences of size N

2/3

, Funnelsort these se-

quences recursively, and merge the resulting sorted sub-

sequences using an N

1/3

-merger.(2)Ak-merger is recur-

sively deﬁned to perform binary merging of k input se-

quences in a clever schedule with an appropriate recur-

sive layout of data in memory using buﬀers to hold sus-

pended merging processes (see Fig. 1). Subsequently two

simpliﬁcations were made, without sacriﬁcing the asymp-

totic number of block transfers performed. In [3]itwas

proved that the binary merging could be performed lazily,

simplifying the scheduling of merging. In [5]itwasfur-

ther observed that the recursive layout of k-mergers is not

necessary.Itissuﬃcientthatak-merger is stored in a con-

secutive array, i. e. the buﬀers can be laid out in arbitrary

order which simpliﬁes the construction algorithm for the

k-merger.

Implicit Cache-Oblivious Sorting

Franceschini in [7] showed how to perform optimal cache-

oblivious sorting implicitly using only O(1) space, i. e. all

data is stored in the input array except for O(1) additional

words of information. In particular the output array is just

a permutation of the input array.

TheRoleoftheTallCacheAssumption

The role of the tall cache assumption on cache-oblivious

sorting was studied by Brodal and Fagerberg in [4]. If no

tall cache assumption is made, they proved the following

theorem:

Theorem 1 ([4], Corollary 3) Let B

=1and B

= M/2.

For any cache-oblivious comparison-based sorting algo-

rithm, let t

and t

be upper bounds on the number of I/Os

performed for block sizes B

and B

.Ifforarealnum-

ber d  0 it is satisﬁed that t

= d 

log

M/B

then

> 1/8  N log

N/M.

The theorem shows cache-oblivious comparison-based

sorting without a tall cache assumption cannot match the

performance of algorithms in the I/O model where M and