Kao M.-Y. (ed.) Encyclopedia of Algorithms

Подождите немного. Документ загружается.

Attribute-Efficient Learning A 77

Atomic Scan

 Snapshots in Shared Memory

Atomic Selfish Flows

 Best Response Algorithms for Selﬁsh Routing

Attribute-Efficient Learning

1987; Littlestone

JYRKI KIVINEN

Department of Computer Science, University of Helsinki,

Helsinki, Finland

Keywords and Synonyms

Learning with irrelevant attributes

Problem Definition

Given here is a basic formulation using the online mistake

bound model, which was used by Littlestone [9]inhissem-

inal work.

Fix a class C of Boolean functions over n variables. To

start a learning scenario, a target function f



2 C is cho-

sen but not revealed to the learning algorithm.Learning

then proceeds in a sequence of trials.Attrialt,aninput

2f0; 1g

is ﬁrst given to the learning algorithm. The

learning algorithm then produces its prediction

,which

is its guess as to the unknown value f



). The correct

value y

= f



) is then revealed to the learner. If y

the learning algorithm made a mistake. The learning algo-

rithm learns C with mistake bound m,ifthenumberof

mistakes never exceeds m, no matter how many trials are

made and how f



and x

; x

;:::are chosen.

Variable (or attribute) X

is relevant for func-

tion f :

0; 1

if f (x

;:::;x

) ¤

f (x

;:::;1  x

;:::;x

) holds for some

x 2 0; 1

.Sup-

pose now that for some k n, every function f 2 C has

at most k relevant variables. It is said that a learning algo-

rithm learns class C attribute-eﬃciently,ifitlearnsC with

a mistake bound polynomial in k and log n. Additionally,

the computation time for each trial is usually required to

be polynomial in n.

Key Results

The main part of current research of attribute-eﬃcient

learning stems from Littlestones Winnow algorithm [9].

The basic version of Winnow maintains a weight vec-

tor w

=(w

t;1

;:::;w

t;n

) 2 R

.Thepredictionforinput

0; 1

is given by

=sign

i=1

t;i

 

where  is a parameter of the algorithm. Initially w

(1;:::;1), and after trial t each component w

t, i

is updated

according to

t+1;i

˛w

t;i

if y

=1,

=0andx

t;i

/˛ if y

=0,

=1andx

t;i

otherwise

(1)

where ˛>1 is a learning rate parameter.

Littlestone’s basic result is that with a suitable choice

of  and ˛, Winnow learns the class of monotone k-literal

disjunctions with mistake bound O(k log n). Since the al-

gorithm changes its weights only when a mistake occurs,

this bound also guarantees that the weights remain small

enough for computation times to remain polynomial in

n. With simple transformations, Winnow also yields at-

tribute-eﬃcient learning algorithms for general disjunc-

tions and conjunctions. Various subclasses of DNF formu-

las and decision lists [8] can be learned, too.

Winnow is quite robust against noise, i. e., errors in in-

put data. This is extremely important for practical applica-

tions. Remove now the assumption about a target func-

tion f



2 C satisfying y

= f



)forallt.Deﬁneattribute

error of a pair (x; y) with respect to a function f as the

minimum Hamming distance between x and x

such that

f (x

)=y. The attribute error of a sequence of trials with

respect to f is the sum of attribute errors of the individual

pairs (x

; y

). Assuming the sequence of trials has attribute

error at most A with respect to some k-literal disjunc-

tion, Auer and Warmuth [1] show that Winnow makes

O(A + k log n) mistakes. The noisy scenario can also be

analyzed in terms of hinge loss [5].

The update rule (1) has served as a model for a whole

family of multiplicative update algorithms. For example,

Kivinen and Warmuth [7] introduce the Exponentiated

Gradient algorithm, which is essentially Winnow modiﬁed

for continuous-valued prediction, and show how it can be

motivated by a relative entropy minimization principle.

Consider a function class C where each function can

be encoded using O(p(k)logn)bitsforsomepolynomial

p. An example would be Boolean formulas with k rele-

vant variables, when the size of the formula is restricted

to p(k) ignoring the size taken by the variables. The cardi-

nality of C is then jCj =2

O(p(k)logn)

. The classical Halving

78 A Automated Search Tree Generation

Algorithm (see [9] for discussion and references) learns

any class consisting of m Boolean functions with mistake

bound log

m, and would thus provide an attribute-eﬃ-

cient algorithm for such a class C. However, the running

time would not be polynomial. Another serious drawback

would be that the Halving Algorithm does not tolerate any

noise. Interestingly, a multiplicative update similar to (1)

has been used in Littlestone and Warmuth’s Weighted

Majority Algorithm [10], and also Vovk’s Aggregating Al-

gorithm [14], to produce a noise-tolerant generalization of

the Halving Algorithm.

Attribute-eﬃcient learning has also been studied in

other learning models than the mistake bound model, such

as Probably Approximately Correct learning [4], learning

with uniform distribution [12], and learning with mem-

bership queries [3]. The idea has been further developed

into learning with a potentially inﬁnite number of at-

tributes [2].

Applications

Attribute-eﬃcient algorithms for simple function classes

have a potentially interesting application as a component

in learning more complex function classes. For exam-

ple, any monotone k-term DNF formula over variables

,:::,x

can be represented as a monotone k-literal dis-

junction over 2

variables z

,wherez

i2A

for A 

1;:::;n

is deﬁned. Running Winnow with the trans-

formed inputs z 2

0; 1

would give a mistake bound

O(k log 2

)=O(kn). Unfortunately the running time

would be linear in 2

, at least for a naive implementa-

tion. Khardon et al. [6] provide discouraging computa-

tional hardness results for this potential application.

Online learning algorithms have a natural application

domain in signal processing. In this setting, the sender

emits a true signal y

at time t,fort =1; 2; 3;:::.Atsome

later time (t + d), a receiver receives a signal z

,whichis

a sum of the original signal y

and various echoes of earlier

signals y

, t

< t, all distorted by random noise. The task

is to recover the true signal y

based on received signals

; z

t1

;:::; z

tl

over some time window l. Currently at-

tribute-eﬃcient algorithms are not used for such tasks, but

see [11] for preliminary results.

Attribute-eﬃcient learning algorithms are similar in

spirit to statistical methods that ﬁnd sparse models. In par-

ticular, statistical algorithms that use L

regularization are

closely related to multiplicative algorithms such as Win-

now and Exponentiated Gradient. In contrast, more clas-

sical L

regularization leads to algorithms that are not at-

tribute-eﬃcient [13].

Cross References

 Boosting Textual Compression

 Learning DNF Formulas

Recommended Reading

1. Auer, P., Warmuth, M.K.: Tracking the best disjunction. Mach.

Learn. 32(2), 127–150 (1998)

2. Blum, A., Hellerstein, L., Littlestone, N.: Learning in the pres-

ence of finitely or infinitely many irrelevant attributes. J. Comp.

Syst. Sci. 50(1), 32–40 (1995)

3. Bshouty, N., Hellerstein, L.: Attribute-efficient learning in query

and mistake-bound models. J. Comp. Syst. Sci. 56(3), 310–319

(1998)

4. Dhagat, A., Hellerstein, L.: PAC learning with irrelevant at-

tributes. In: Proceedings of the 35th Annual Symposium on

Foundations of Computer Science, Santa Fe, pp 64–74. IEEE

Computer Society, Los Alamitos (1994)

5. Gentile, C., Warmuth, M.K.: Linear hinge loss and average mar-

gin. In: Kearns, M.J., Solla, S.A., Cohn, D.A. (eds.) Advances in

neural information processing systems 11, p. 225–231. MIT

Press, Cambridge (1999)

6. Khardon, R., Roth, D., Servedio, R.A.: Efficiency versus conver-

gence of boolean kernels for on-line learning algorithms. J. Ar-

tif. Intell. Res. 24, 341–356 (2005)

7. Kivinen, J., Warmuth, M.K.: Exponentiated gradient versus gra-

dient descent for linear predictors. Inf. Comp. 132(1), 1–64

(1997)

8. Klivans, A.R. Servedio, R.A.: Toward attribute efficient learning

of decision lists and parities. J. Mach. Learn. Res. 7(Apr), 587–

602 (2006)

9. Littlestone, N.: Learning quickly when irrelevant attributes

abound: A new linear threshold algorithm. Mach. Learn. 2(4),

285–318 (1988)

10. Littlestone, N., Warmuth, M.K.: The weighted majority algo-

rithm. Inf. Comp. 108(2), 212–261 (1994)

11. Martin, R.K., Sethares, W.A., Williamson, R.C., Johnson, Jr., C.R.:

Exploiting sparsity in adaptive filters. IEEE Trans. Signal Pro-

cess. 50(8), 1883–1894 (2002)

12. Mossel, E., O’Donnell, R., Servedio, R.A.: Learning functions of

k relevant variables. J. Comp. Syst. Sci. 69(3), 421–434 (2004)

13. Ng, A.Y.: Feature selection, L

vs. L

regularization, and rota-

tional invariance. In: Greiner, R., Schuurmans, D. (eds.) Proceed-

ings of the 21st International Conference on Machine Learn-

ing, pp 615–622. The International Machine Learning Society,

Princeton (2004)

14. Vovk,V.:Aggregatingstrategies.In:Fulk,M.,Case,J.(eds.)

Proceedings of the 3rd Annual Workshop on Computational

Learning Theory, p. 371–383. Morgan Kaufmann, San Mateo

(1990)

Automated Search Tree Generation

2004; Gramm, Guo, Hüffner, Niedermeier

FALK HÜFFNER

Department of Math and Computer Science,

University of Jena, Jena, Germany

Automated Search Tree Generation A 79

Keywords and Synonyms

Automated proofs of upper bounds on the running time

of splitting algorithms

Problem Definition

This problem is concerned with the automated develop-

ment and analysis of search tree algorithms. Search tree

algorithms are a popular way to ﬁnd optimal solutions to

NP-complete problems.

The idea is to recursively solve

several smaller instances in such a way that at least one

branch is a yes-instance if and only if the original instance

is. Typically, this is done by trying all possibilities to con-

tribute to a solution certiﬁcate for a small part of the input,

yielding a small local modiﬁcation of the instance in each

branch.

For example, consider the NP-complete C

LUSTER

EDITING problem: can a given graph be modiﬁed by

adding or deleting up to k edges such that the resulting

graph is a cluster graph, that is, a graph that is a disjoint

union of cliques? To give a search tree algorithm for C

LUS-

TER EDITING, one can use the fact that cluster graphs are

exactly the graphs that do not contain a P

(a path of

3 vertices) as an induced subgraph. One can thus solve

LUSTER EDITING by ﬁnding a P

and splitting it into

3 branches: delete the ﬁrst edge, delete the second edge,

or add the missing edge. By this characterization, when-

ever there is no P

found, one already has a cluster graph.

The original instance has a solution with k modiﬁcations if

andonlyifatleastoneofthebrancheshasasolutionwith

k  1 modiﬁcations.

Analysis

For NP-complete problems, the running time of a search

tree algorithm only depends on the size of the search tree

up to a polynomial factor , which depends on the num-

ber of branches and the reduction in size of each branch.

If the algorithm solves a problem of size s and calls it-

self recursively for problems of sizes s  d

;:::;s  d

then (d

;:::;d

) is called the branching vector of this re-

cursion. It is known that the size of the search tree is

then O(˛

), where the branching number ˛ is the only pos-

itive real root of the characteristic polynomial

 z

dd

z

dd

; (1)

where d =maxfd

;:::;d

g.ForthesimpleCLUSTER

EDITING search tree algorithm and the size measure k,the

For ease of presentation, only decision problems are considered;

adaption to optimization problems is straightforward.

branching vector is (1, 1, 1) and the branching number is 3,

meaning that the running time is up to a polynomial fac-

tor O(3

Case Distinction

Often, one can obtain better running times by distinguish-

ing a number of cases of instances, and giving a specialized

branching for each case. The overall running time is then

determined by the branching number of the worst case.

Several publications obtain such algorithms by hand (e. g.,

a search tree of size O(2.27

)forCLUSTER EDITING [4]);

the topic of this work is how to automate this. That is, the

problem is the following:

Problem 1 (Fast Search Tree Algorithm)

NPUT:AnNP-hardproblemP and a size measure s(I) of

an instance I of

P where instances I with s(I)=0can be

solved in polynomial time.

UTPUT: A partition of the instance set of P into cases, and

for each case a branching such that the maximum branch-

ing number over all branchings is as small as possible.

Note that this problem deﬁnition is somewhat vague; in

particular, to be useful, the case an instance belongs to

must be recognizable quickly. It is also not clear whether

an optimal search tree algorithm exists; conceivably, the

branching number can be continuously reduced by in-

creasingly complicated case distinctions.

Key Results

Gramm et al. [3] describe a method to obtain fast search

tree algorithms for C

LUSTER EDITING and related prob-

lems,wherethesizemeasureisthenumberofeditingop-

erations k. To get a case distinction, a number of subgraphs

are enumerated such that each instance is known to con-

tain at least one of these subgraphs. It is next described

how to obtain a branching for a particular case.

A standard way of systematically obtaining specialized

branchings for instance cases is to use a combination of

basic branching and data reduction rules. Basic branching

is typically a very simple branching technique, and data re-

duction rules replace an instance with a smaller, solution-

equivalent instance in polynomial time. Applying this to

LUSTER EDITING ﬁrst requires a small modiﬁcation of

the problem: one considers an annotated version, where

an edge can be marked as permanent and a non-edge can

be marked as forbidden. Any such annotated vertex pair

cannot be edited anymore. For a pair of vertices, the basic

branching then branches into two cases: permanent or for-

bidden (one of these options will require an editing opera-

tion). The reduction rules are: if two permanent edges are

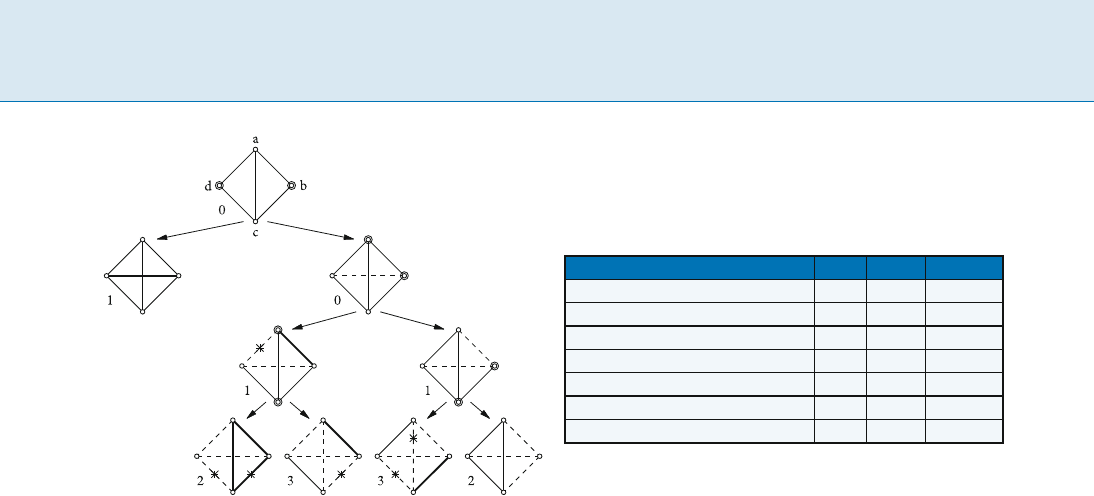
80 A Automated Search Tree Generation

Automated Search Tree Generation, Figure 1

Branching for a C

LUSTER EDITI NG case using only basic branch-

ing on vertex pairs (double circles), and a pplications of the re-

duction rules (asterisks). Permanent edges are marked bold,

forbidden edges dashed.Thenumbers next to the subgraphs

state the change of the problem size k. The branching vector

is(1,2,3,3,2),correspondingtoasearchtreesizeofO(2.27

)

adjacent, the third edge of the triangle they induce must

also be permanent; and if a permanent and a forbidden

edge are adjacent, the third edge of the triangle they in-

duce must be forbidden.

Figure 1 shows an example branching derived in this

way.

Using a reﬁned method of searching the space for all

possible cases and to distinguish all branchings for a case,

Gramm et al. [3] derive a number of search tree algorithms

for graph modiﬁcation problems.

Applications

Gramm et al. [3] apply the automated generation of search

tree algorithms to several graph modiﬁcation problems

(see also Table 1). Further, Hüﬀner [5]demonstratesan

application of D

OMINATING SET on graphs with maxi-

mumdegree4,wherethesizemeasureisthesizeofthe

dominating set.

Fedin and Kulikov [2]examinevariantsofSAT;how-

ever, their framework is limited in that it only proves up-

per bounds for a ﬁxed algorithm instead of generating al-

gorithms.

Skjernaa [6] also presents results on variants of SAT.

His framework does not require user-provided data reduc-

tion rules, but determines reductions automatically.

Automated Search Tree Generation, Table 1

Summary of search tree sizes where automation gave improve-

ments. “Known” is the size of the best previously published

“hand-made” search tree. For the satisfiability problems, m is the

number of clauses and l is the length of the formula

Problem Trivial Known New

CLUSTER EDITING 3 2.27 1.92 [3]

CLUSTER DELETION 2 1.77 1.53 [3]

CLUSTER VERTEX DELETION 3 2.27 2.26 [3]

BOUNDED DEGREE DOMINATINGSET 4 3.71 [5]

X3SAT, size measure m 3 1.1939 1.1586 [6]

(n,3)-MAXSAT, size measure m 2 1.341 1.2366 [2]

(n,3)-MAXSAT, size measure l 2 1.1058 1.0983 [2]

Open Problems

The analysis of search tree algorithms can be much

improved by describing the “size” of an instance by

more than one variable, resulting in multivariate recur-

rences [1]. It is open to introduce this technique into an

automation framework.

It has frequently been reported that better running

time bounds obtained by distinguishing a large number

of cases do not necessarily speed up, but in fact can slow

down, a program. A careful investigation of the tradeoﬀs

involved and a corresponding adaption of the automation

frameworks is an open task.

Experimental Results

Gramm et al. [3]andHüﬀner[5] report search tree sizes

for several NP-complete problems. Further, Fedin and Ku-

likov [2]andSkjernaa[6] report on variants of satisﬁabil-

ity. Table 1 summarizes the results.

Cross References

 Vertex Cover Search Trees

Acknowledgments

Partially supported by the Deutsche Forschungsgemeinschaft, Emmy

Noether research group PIAF (ﬁxed-parameter algorithms), NI

369/4.

Recommended Reading

1. Eppstein, D.: Quasiconvex analysis of backtracking algorithms.

In: Proc. 15th SODA, ACM/SIAM, pp. 788–797 (2004)

2. Fedin, S.S., Kulikov, A.S.: Automated proofs of upper bounds

on the running time of splitting algorithms. J. Math. Sci. 134,

2383–2391 (2006). Improved results at http://logic.pdmi.ras.ru/

~kulikov/autoproofs.html

Automated Search Tree Generation A 81

3. Gramm, J., Guo, J., Hüffner, F., Niedermeier, R.: Automated gen-

eration of search tree algorithms for hard graph modification

problems. Algorithmica 39, 321–347 (2004)

4. Gramm, J., Guo, J., Hüffner, F., Niedermeier, R.: Graph-modeled

data clustering: Exact algorithms for clique generation. Theor.

Comput. Syst. 38, 373–392 (2005)

5. Hüffner, F.: Graph Modification Problems and Automated

Search Tree Generation. Diplomarbeit, Wilhelm-Schickard-Insti-

tut für Informatik, Universität Tübingen (2003)

6. Skjernaa, B.: Exact Algorithms for Variants of Satisfiability and

Colouring Problems. Ph. D. thesis, University of Aarhus, Depart-

ment of Computer Science (2004)

Backtracking Based k-SAT Algorithms B 83

Backtracking Based k-SAT

Algorithms

2005; Paturi, Pudlák, Saks, Zane

RAMAMOHAN PATURI

,PAVEL PUDLÁK

ICHAEL SAKS

,FRANCIS ZANE

Department of Computer Science and Engineering,

University of California at San Diego,

San Diego, CA, USA

Mathematical Institute, Academy of Science

of the Czech Republic, Prague, Czech Republic

Department of Mathematics, Rutgers, State University

of New Jersey, Piscataway, NJ, USA

Bell Laboraties, Lucent Technologies,

Murray Hill, NJ, USA

Problem Definition

Determination of the complexity of k-CNF satisﬁability is

a celebrated open problem: given a Boolean formula in

conjunctive normal form with at most k literals per clause,

ﬁnd an assignment to the variables that satisﬁes each of the

clauses or declare none exists. It is well-known that the de-

cision problem of k–CNF satisﬁability is NP-complete for

k  3. This entry is concerned with algorithms that signif-

icantly improve the worst case running time of the naive

exhaustive search algorithm, which is poly(n)2

for a for-

mula on n variables. Monien and Speckenmeyer [8]gave

the ﬁrst real improvement by giving a simple algorithm

whose running time is O(2

(1"

), with "

> 0forallk.

In a sequence of results [1,3,5,6,7,9,10,11,12], algorithms

with increasingly better running times (larger values of "

)

have been proposed and analyzed.

These algorithms usually follow one of two lines of at-

tack to ﬁnd a satisfying solution. Backtrack search algo-

rithms make up one class of algorithms. These algorithms

were originally proposed by Davis, Logemann and Love-

land [4] and are sometimes called Davis–Putnam proce-

dures. Such algorithms search for a satisfying assignment

by assigning values to variables one by one (in some or-

der), backtracking if a clause is made false. The other class

of algorithms is based on local searches (the ﬁrst guaran-

teed performance results were obtained by Schöning [12]).

One starts with a randomly (or strategically) selected as-

signment, and searches locally for a satisfying assignment

guided by the unsatisﬁed clauses.

This entry presents ResolveSat,arandomizedalgo-

rithm for k-CNF satisﬁability which achieves some of the

best known upper bounds. ResolveSat isbasedonanear-

lier algorithm of Paturi, Pudlák and Zane [10], which is es-

sentially a backtrack search algorithm where the variables

are examined in a randomly chosen order. An analysis of

the algorithm is based on the observation that as long as

the formula has a satisfying assignment which is isolated

from other satisfying assignments, a third of the variables

are expected to occur as unit clauses as the variables are

assigned in a random order. Thus, the algorithm needs to

correctly guess the values of at most 2/3 of the variables.

This analysis is extended to the general case by observing

that there either exists an isolated satisfying assignment, or

there are many solutions so the probability of guessing one

correctly is suﬃciently high.

ResolveSat combines these ideas with resolution to

obtain signiﬁcantly improved bounds [9]. In fact, Re-

solveSat obtains the best known upper bounds for k-

CNF satisﬁability for all k  5. For k =3and4,Iwama

and Takami [6] obtained the best known upper bound

with their randomized algorithm which combines the

ideas from Schöning’s local search algorithm and Re-

solveSat. Furthermore, for the promise problem of unique

k-CNF satisﬁability whose instances are conjectured to be

among the hardest instances of k-CNF satisﬁability [2],

ResolveSat holds the best record for all k  3. Bounds ob-

tained by ResolveSat for unique k-SAT and k-SAT, for

k =3; 4; 5; 6areshowninTable1. Here, these bounds are

compared with those of of Schöning [12], subsequently

improved results based on local search [1,5,11], and the

most recent improvements due to Iwama and Takami [6

The upper bounds obtained by these algorithms are ex-

84 B Backtracking Based k-SAT Algorithms

pressed in the form 2

cno(n)

and the numbers in the table

represent the exponent c. This comparison focuses only on

the best bounds irrespective of the type of the algorithm

(randomized versus deterministic).

Notation In this entry, a CNF boolean formula F(x

;

;:::;x

) is viewed as both a boolean function and a set

of clauses. A boolean formula F is a k-CNF if all the clauses

have size at most k.ForaclauseC,writevar(C)fortheset

of variables appearing in C.Ifv 2 var(C), the orientation

of v is positive if the literal v is in C and is negative if

is in C.RecallthatifF is a CNF boolean formula on vari-

ables (x

; x

;:::;x

)anda is a partial assignment of the

variables, the restriction of F by a is deﬁned to be the for-

mula F

= Fd

on the set of variables that are not set by

a, obtained by treating each clause C of F as follows: if C

is set to 1 by a then delete C,andotherwisereplaceC by

the clause C

obtained by deleting any literals of C that are

set to 0 by a.Finally,aunit clause is a clause that contains

exactly one literal.

Key Results

ResolveSat Algorithm

The ResolveSat algorithm is very simple. Given a k-CNF

formula, it ﬁrst generates clauses that can be obtained by

resolution without exceeding a certain clause length. Then

it takes a random order of variables and gradually assigns

values to them in this order. If the currently considered

variable occurs in a unit clause, it is assigned the only value

that satisﬁes the clause. If it occurs in contradictory unit

clauses, the algorithm starts over. At each step, the algo-

rithm also checks if the formula is satisﬁed. If the formula

is satisﬁed, then the input is accepted. This subroutine is

repeated until either a satisfying assignment is found or

a given time limit is exceeded.

The ResolveSat algorithm uses the following subrou-

tine, which takes an arbitrary assignment y,aCNFformula

F, and a permutation  as input, and produces an assign-

ment u. The assignment u is obtained by considering the

variables of y in the order given by  and modifying their

values in an attempt to satisfy F.

Function Modify(CNF formula G(x

; x

;:::;x

), permu-

tation  of f1; 2;:::;ng, assignment y) ! (assignment

= G.

for i =1to n

if G

i1

contains the unit clause x

(i)

then u

(i)

else if G

i1

contains the unit clause

(i)

then u

(i)

else u

(i)

= y

(i)

= G

i1

(i)

end /* end for loop */

return u;

The algorithm Search is obtained by running Modi-

fy(G;;y) on many pairs (; y), where  is a random

permutation and y is a random assignment.

Search(CNF-formula F, integer I)

repeat I times

 = uniformly random permutation of 1;:::;n

y = uniformly random vector 2f0; 1g

u = Modify(F;;y);

if u satisﬁes F

then output(u); exit;

end/* end repeat loop */

output(‘Unsatisﬁable’);

The ResolveSat algorithm is obtained by combining

Search with a preprocessing step consisting of bounded

resolution.FortheclausesC

and C

, C

and C

conﬂict

on variable v if one of them contains v and the other

contains

v. C

and C

is a resolvable pair if they conﬂict

on exactly one variable v.Forsuchapair,theirresolvent,

denoted R(C

; C

), is the clause C = D

_ D

where D

and D

are obtained by deleting v and

v from C

and C

It is easy to see that any assignment satisfying C

and C

also satisﬁes C.Hence,ifF is a satisﬁable CNF formula

containing the resolvable pair C

; C

then the formula

= F ^ R(C

; C

) has the same satisfying assignments as

F. The resolvable pair C

; C

is s-bounded if jC

j; jC

js

and jR(C

; C

)js. The following subroutine extends

aformulaF to a formula F

by applying as many steps of

s-bounded resolution as possible.

Resolve(CNF Formula F, integer s)

= F.

while F

has an s-bounded resolvable pair C

; C

with R(C

; C

) 62 F

= F

^ R(C

; C

return (F

The algorithm for k-SAT is the following simple combina-

tion of Resolve and Search:

ResolveSat(CNF-formula F, integer s, positive integer I)

= Resolve(F; s).

Search(F

; I).

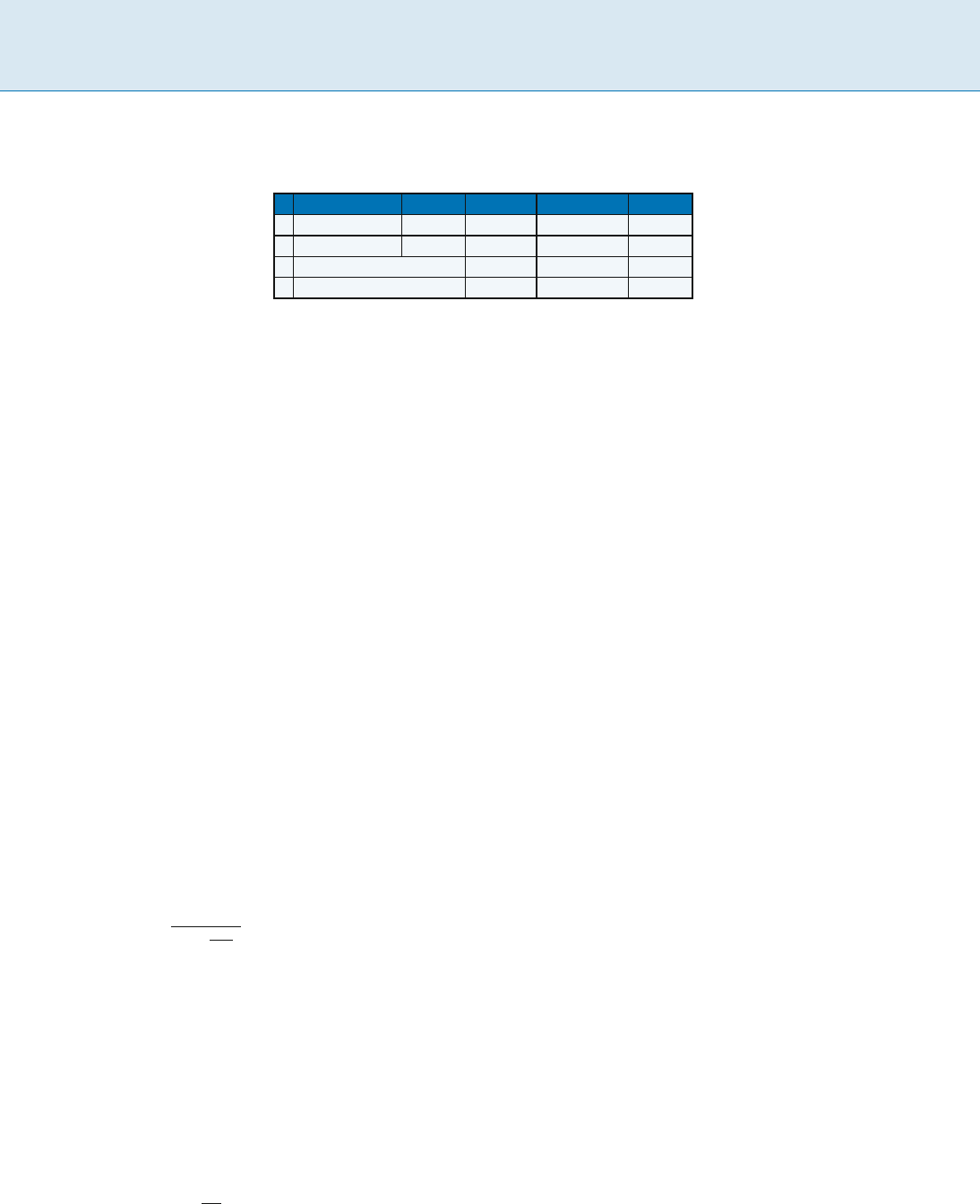
Backtracking Based k-SAT Algorithms B 85

Backtracking Based k-SAT Algorithms, Table 1

This table shows the exponent c in the bound 2

cno(n)

for the unique k-SAT and k-SAT from the ResolveSat algorithm, the bounds

for k-SAT from Schöning’s algorithm [12], its improved versions for 3-SAT [1,5 ,11], and the hybrid version of [6]

k unique k-SAT [9] k-SAT [9] k-SAT [12] k-SAT [1,5,11] k-SAT [6]

3 0.386 . . . 0.521 . . . 0.415 . . . 0.409 . . . 0.404 ...

4 0.554 . . . 0.562 . . . 0.584 . . . 0.559 ...

5 0.650 . . . 0.678 . . .

6 0.711 . . . 0.736 . . .

Analysis of ResolveSat

The running time of ResolveSat(F; s; I) can be bounded

as follows. Resolve(F; s) adds at most O(n

)clausestoF

by comparing pairs of clauses, so a naive implementation

runs in time n

poly(n) (this time bound can be improved,

but this will not aﬀect the asymptotics of the main re-

sults). Search(F

; I)runsintimeI(jFj + n

)poly(n). Hence

the overall running time of ResolveSat(F; s; I)iscrudely

bounded from above by (n

+ I(jFj+ n

))poly(n). If

s = O(n/logn), the overall running time can be bounded

by IjFj2

O(n)

since n

O(n)

.Itwillbesuﬃcienttochoose

s either to be some large constant or to be a slowly growing

function of n.Thatis,s(n) tends to inﬁnity with n but is

O(log n).

The algorithm Search(F; I) always answers “unsatis-

ﬁable” if F is unsatisﬁable. Thus the only problem is to

place an upper bound on the error probability in the case

that F is satisﬁable. Deﬁne (F) to be the probability that

Modify(F;;y) ﬁnds some satisfying assignment. Then

for a satisﬁable F the error probability of Search(F; I)is

equal to (1   (F))

 e

I(F)

,whichisatmoste

n

pro-

vided that I  n/ (F). Hence, it suﬃces to give good upper

bounds on  (F).

Complexity analysis of ResolveSat requires certain

constants 

for k  2:



j=1

j(j +

k1

)

It is straightforward to show that 

=4 4ln2> 1:226

using Taylor’s series expansion of ln 2. Using standard

facts, it is easy to show that 

is an increasing function

of k with the limit

j=1

(1/j

)=(

/6) = 1:644 :::

The results on the algorithm ResolveSat are summa-

rized in the following three theorems.

Theorem 1 (i) Let k  5,andlets(n) be a function going

to inﬁnity. Then for any satisﬁable k-CNF formula F on n

variables,

(F

)  2

(1



k1

)no(n)

Hence, ResolveSat(F; s; I) with I =2

(1

/(k1))n+O(n)

has error probability O(1) and running time

(1

/(k1))n+O(n)

on any satisﬁable k-CNF formula, pro-

vided that s(n) goes to inﬁnity suﬃciently slowly.

(ii) For k  3, the same bounds are obtained provided

that F is uniquely satisﬁable.

Theorem 1 is proved by ﬁrst considering the uniquely

satisﬁable case and then relating the general case to the

uniquely satisﬁable case. When k  5, the analysis reveals

that the asymptotics of the general case is no worse than

that of the uniquely satisﬁable case. When k =3ork =4,

it gives somewhat worse bounds for the general case than

for the uniquely satisﬁable case.

Theorem 2 Let s = s(n) be a slowly growing function. For

any satisﬁable n-variable 3-CNF formula, (F

)  2

0:521n

and so ResolveSat(F; s; I) with I = n2

0:521n

has error prob-

ability O(1) and running time 2

0:521n+O(n)

Theorem 3 Let s = s(n) be a slowly growing function.

For any satisﬁable n-variable 4-CNF formula, (F

) 

0:5625n

,andsoResolveSat(F; s; I) with I = n2

0:5625n

has

error probability O(1) and running time 2

0:5625n+O(n)

Applications

Various heuristics have been employed to produce imple-

mentations of 3-CNF satisﬁability algorithms which are

considerably more eﬃcient than exhaustive search algo-

rithms. The ResolveSat algorithm and its analysis provide

a rigorous explanation for this eﬃciency and identify the

structural parameters (for example, the width of clauses

and the number of solutions), inﬂuencing the complexity.

Open Problems

The gap between the bounds for the general case and the

uniquely satisﬁable case when k 2f3; 4g is due to a weak-

ness in analysis, and it is conjectured that the asymptotic

bounds for the uniquely satisﬁable case hold in general for

all k. If true, the conjecture would imply that ResolveSat

is also faster than any other known algorithm in the k =3

case.

86 B Best Response Algorithms for Selfish Routing

Another interesting problem is to better understand

the connection between the number of satisfying assign-

ments and the complexity of ﬁnding a satisfying assign-

ment [2]. A strong conjecture is that satisﬁability for for-

mulas with many satisfying assignments is strictly easier

than for formulas with fewer solutions.

Finally, an important open problem is to design an

improved k-SAT algorithm which runs faster than the

bounds presented in here for the unique k-SAT case.

Cross References

 Local Search Algorithms for kSAT

 Maximum Two-Satisﬁability

 Parameterized SAT

 Thresholds of Random k-S

Recommended Reading

1. Baumer, S., Schuler, R.: Improving a Probabilistic 3-SAT Algo-

rithm by Dynamic Search and Independent Clause Pairs. In:

SAT 2003, pp. 150–161

2. Calabro, C., Impagliazzo, R., Kabanets, V., Paturi, R.: The Com-

plexity of Unique k-SAT: An Isolation Lemma for k-CNFs. In:

Proceedings of the Eighteenth IEEE Conference on Computa-

tional Complexity, 2003

3. Dantsin, E., Goerdt, A., Hirsch, E.A., Kannan, R., Kleinberg, J.,

Papadimitriou, C., Raghavan, P., Schöning, U.: A deterministic

(2 

k+1

)

algorithm for k-SAT based on local search. Theor.

Comp. Sci. 289(1), 69–83 (2002)

4. Davis,M.,Logemann,G.,Loveland,D.:Amachineprogramfor

theorem proving. Commun. ACM 5, 394–397 (1962)

5. Hofmeister, T., Schöning, U., Schuler, R., Watanabe, O.: A prob-

abilistic 3–SAT algorithm further improved. In: STACS 2002.

LNCS, vol. 2285, pp. 192–202. Springer, Berlin (2002)

6. Iwama, K., Tamaki, S.: Improved upper bounds for 3-SAT. In:

Proceedings of the fifteenth annual ACM-SIAM symposium on

Discrete algorithms, 2004, pp. 328–329

7. Kullmann, O.: New methods for 3-SAT decision and worst-case

analysis. Theor. Comp. Sci. 223(1–2), 1–72 (1999)

8. Monien, B., Speckenmeyer, E.: Solving Satisfiability In Less Than

Steps. Discret. Appl. Math. 10, 287–295 (1985)

9. Paturi, R., Pudlák, P., Saks, M., Zane, F.: An Improved Exponen-

tial-time Algorithm for k-SAT. J. ACM 52(3), 337–364 (2005) (An

earlier version presented in Proceedings of the 39th Annual

IEEE Symposium on Foundations of Computer Science, 1998,

pp. 628–637)

10. Paturi, R., Pudlák, P., Zane, F.: Satisfiability Coding Lemma. In:

Proceedings of the 38th Annual IEEE Symposium on Foun-

dations of Computer Science, 1997, pp. 566–574. Chicago J.

Theor. Comput. Sci. (1999), http://cjtcs.cs.uchicago.edu/

11. Rolf, D.: 3-SAT 2RTIME(1:32971

). In: ECCC TR03-054, 2003

12. Schöning, U.: A probabilistic algorithm for k-SAT based on lim-

ited local search and restart. Algorithmica 32, 615–623 (2002)

(An earlier version appeared in 40th Annual Symposium on

Foundations of Computer Science (FOCS ’99), pp. 410–414)

Best Response Algorithms

for Selfish Routing

2005; Fotakis, Kontogiannis, Spirakis

PAUL SPIRAKIS

Computer Engineering and Informatics, Research

and Academic Computer Technology Institute,

Patras University, Patras, Greece

Keywords and Synonyms

Atomic selﬁsh ﬂows

Problem Definition

A setting is assumed in which n selﬁsh users compete for

routing their loads in a network. The network is an s  t

directed graph with a single source vertex s and a single

destination vertex t. The users are ordered sequentially.

It is assumed that each user plays after the user before

her in the ordering, and the desired end result is a Pure

Nash Equilibrium (PNE for short). It is assumed that, when

a user plays (i. e. when she selects an s  t path to route

her load), the play is a best response (i. e. minimum de-

lay), given the paths and loads of users currently in the net.

The problem then is to ﬁnd the class of directed graphs for

which such an ordering exists so that the implied sequence

of best responses leads indeed to a Pure Nash Equilibrium.

The Model

A network congestion game is a tuple

(

)

i2N

; G; (d

)

e2E

)

where N = f1;:::;ng is the set of users where user i con-

trols w

units of traﬃc demand. In unweighted conges-

tion games w

=1for i =1;:::;n. G(V,E)isadirected

graph representing the communications network and d

is the latency function associated with edge e 2 E.Itisas-

sumed that the d

’s are non-negative and non-decreasing

functions of the edge loads. The edges are called identi-

cal if d

(x)=x; 8e 2 E. The model is further restricted

to single-commodity network congestion games, where G

has a single source s and destination t and the set of users’

strategies is the set of s  t paths, denoted P.Withoutloss

of generality it is assumed that G is connected and that ev-

ery vertex of G lies on a directed s  t path.

A vector P =(p

;:::;p

) consisting of an s  t

path p

for each user i is a pure strategies proﬁle.Let

(P)=

i:e2p

be the load of edge e in P.Theauthors

deﬁne the cost 

(P)foruseri routing her demand on

Best Response Algorithms for Selfish Routing B 87

path p in the proﬁle P to be



(P)=

e2p\p

(

(P)

)

e2pXp

(

(P)+w

)

The cost 

(P)ofuseri in P is just 

(P), i. e. the total

delay along her path.

ApurestrategiesproﬁleP is a Pure Nash Equilibrium

(PNE) iﬀ no user can reduce her total delay by unilaterally

deviating i. e. by selecting another s  t path for her load,

while all other users keep their paths.

Best Response

Let p

be the path of user i and P



;:::;p



be the

pure strategies proﬁle for users 1;:::;i. Then the best re-

sponse of user i +1isapathp

i+1

so that

i+1

= avg min

p2P

e2p





+ w

i+1



;

Flows and Common Best Response

A (feasible) ﬂow on the set P of s  t paths of G is a func-

tion

: P !<

0

so that

p2P

i=1

The single-commodity network congestion game

(

)

i2N

; G; (d

)

e2E

)

has the Common Best Response

property if for every initial ﬂow

(not necessarily feasible),

all users have the same set of best responses with respect

.Thatis,ifapathp is a best response with respect to

for some user, then for all users j and all paths p

e2p0



+ w





e2p



+ w



Furthermore, every segment  of a best response

path p is a best response for routing the demand of any

user between ’s endpoints. It is allowed here that some

users may already have contributed to the initial ﬂow

Layered and Series-Parallel Graphs

A directed (multi)graph G(V, E) with a distinguished

source s and destination t is layered iﬀ all directed s  t

paths have exactly the same length and each vertex lies on

some directed s  t path.

Amultigraphisseries-parallel with terminals (s, t)if

1. it is a single edge (s, t)or

2. it is obtained from two series-parallel graphs G

; G

with terminals (s

; t

)and(s

; t

) by connecting them

either in series or in parallel. In a series connection, t

is identiﬁed with s

and s

becomes s and t

becomes t.

In a parallel connection, s

= s

= s and t

= t

= t.

Key Results

The Greedy Best Response Algorithm (GBR)

GBR considers the users one-by-one in non-increasing or-

der of weight (i. e. w

 w

w

). Each user adopts

her best response strategy on the set of (already adopted

in the net) best responses of previous users. No user can

change her strategy in the future. Formally, GBR succeeds

if the eventual proﬁle P is a Pure Nash Equilibrium (PNE).

The Characterization

In [3]itisshown:

Theorem 1 If G is an (s  t) series-parallel graph and the

game

(

)

i2N

; G; (d

)

e2E

)

has the common best response

property, then GBR succeeds.

Theorem 2 A weighted single-commodity network conges-

tion game in a layered network with identical edges has the

common best response property for any set of user weights.

Theorem 3 For any single-commodity network congestion

game in series-parallel networks, GBR succeeds if

1. Theusersareidentical(ifw

=1for all i) and the edge-

delays are arbitrary but non-decreasing or

2. Thegraphislayeredandtheedgesareidentical(forar-

bitrary user weights)

Theorem 4 If the network consists of bunches of parallel-

links connected in series, then a PNE is obtained by applying

GBR to each bunch.

Theorem 5

1. If the network is not series-parallel then there exist games

where GBR fails, even for 2 identical users and identical

edges.

2. If the network does not have the common best response

property (and is not a sequence of parallel links graphs

connected in series) then there exist games where GBR

fails, even for 2-layered series-parallel graphs.

Examples of such games are provided in [3].

Applications

GBR has a natural distributed implementation based on

a leader election algorithm. Each player is now represented

by a process. It is assumed that processes know the net-

work and the edge latency functions. The existence of