Kao M.-Y. (ed.) Encyclopedia of Algorithms

Подождите немного. Документ загружается.

998 U Utilitarian Mechanism Design for Single-Minded Agents

Algorithm A

1 ˛

"2

;

2 for i =1;:::;n do

3 v

:= minfv

; 2

k+1

4 v

:= b˛

v

5returnA

(a; v

);

Algorithm A

FPTAS

1 V := max

, Best := (;;:::;;), bes t := 0;

2 for j =0;:::;dlog(1  ")

1

ne +1do

3 k := blog(V)cj;

4 if w

(a; v)) > best then

5 Best := A

(a; v); be st := w

(a; v));

6returnBest;

Utilitarian Mechanism Design for Single-Minded Agents, Figure 1

A monotone FPTAS for utilitarian problem ˘ and single-minded agents

Monotonicity

A suﬃcient condition for truthfulness of approximate

mechanisms for single-minded CAs was ﬁrst given by

Lehmann et al. [10]. Their results can be adopted for the

considered scenario. An algorithm A is monotone with

respect to R



i 2 S(A((a

; v

); (a

i

; v

i

)))

) i 2 S(A((a

; v

); (a

i

; v

i

)))

for any a

 a

and v

 v

. Intuitively, one requires that

a winning declaration (a

; v

) remains winning if an ob-

ject a

, smaller according to R



,andahighervaluationv

are declared. If declarations (a

i

; v

i

) are ﬁxed and object

declared by i,algorithmA deﬁnes a critical value 

i. e., the minimum valuation v

that makes (a

; v

)win-

ning, i. e., i 2 S(A((a

; v

); (a

i

; v

i

))) for any v

>

and i … S(A((a

; v

); (a

i

; v

i

))) for any v

<

.The

critical value payment scheme p

associated with A is de-

ﬁned by p

(a; v)=

,ifi 2 S(A(a; v)), and p

(a; v)=0,

otherwise. The critical value for any ﬁxed agent i can be

computed, e. g., by performing binary search on interval

[0; v

] and repeatedly running algorithm A to check if i

is selected. Also, mechanism M

=(A; p

)isnormalized,

i. e., agents that are not selected pay 0. Algorithm A is ex-

act, if for declarations (a; v), A(a; v)

= a

or A(a; v)

= ¿

for all i.Inanalogyto[10] one obtains the following.

Theorem 1 Let A be a monotone and exact algorithm

for some utilitarian problem ˘ and single-minded agents.

Then mechanism M

=(A; p

) is truthful.

Additional deﬁnitions

In the unsplittable ﬂow problem (UFP), an undirected

graph G =(V ; E), jEj = m, jVj = n, with edge capacities

, e 2 E,andasetK of k  1 commodities described

by terminal pairs (s

; t

) 2 V  V and a demand d

and

avaluec

are given. One assumes that max

 min

2 [0; 1] for each i 2 K = f1;:::;kg,andb

 1forall

e 2 E.LetB =min

g. A feasible solution is a subset

 K and a single ﬂow s

-t

-path for each i 2 K

,such

that the demands of K

can simultaneously and unsplit-

tably be routed along the paths and the capacities are not

exceeded. The goal in UFP, called B-bounded UFP,isto

maximize the total value of the commodities in K

.Agen-

eralization is allocating bandwidth for multicast com-

munication, where commodity is a set of terminals that

should be connected by a multicast tree.

Key Results

Monotone approximation schemes

Let ˘ be a given utilitarian (maximization) problem.

Given declarations (a; v), let Opt(a; v)denoteanoptimal

solution to ˘ on this instance and w(Opt(a; v)) the cor-

responding social welfare. Assuming that A

is a pseu-

dopolynomial exact algorithm for ˘ an algorithm A

and

monotone FPTAS for ˘ is deﬁned in Fig. 1.

Theorem 2 Let ˘ be a utilitarian mechanism de-

sign problem among single-minded agents, A

mono-

tone pseudopolynomial algorithm for ˘ with running

time poly(n; V ),whereV=max

, and assume that

V  w(Opt(a; v)) for declaration (a; v).ThenA

FPTAS

a monotone FPTAS for ˘ .

Theorem 2 can also be applied to minimization problems.

Section “Applications” describes how these approximation

schemes can be used for forward multi-unit auctions and

job scheduling with deadlines.

Truthful primal-dual mechanisms

For an instance G =(V ; E) of UFP deﬁned above, let

be the set of all s

-t

-paths in G,andS =

i=1

. Given

S 2 S

,letq

(e)=d

if e 2 S,andq

(e)=0otherwise.

Utilitarian Mechanism Design for Single-Minded Agents U 999

Algorithm Greedy-1:

T := ;; K := f1;:::;kg;

2 forall e 2 E do y

:= 1/ b

;

3 repeat

4 forall i 2 K do S

:= argmin

e2S

S 2



;

5 j := argmax

(

e2S

i 2 K

)

;

T := T [fS

g; K := K nfjg;

7 forall e 2 S

do y

:= y





B1



(e)/(b

1)

;

8 until

e2E

 e

B1

m or K = ;;

9return

Utilitarian Mechanism Design for Single-Minded Agents, Figure 2

Truthful mechanism for network (multicast) routing. e  2:718 is Euler number.

UFP is the following integer linear program (ILP)

max

i=1



S2S

(1)

s.t.

S:S2S;e2S

(e)x

 b

8e 2 E (2)

S2S

 1 8i 2f1;:::;kg (3)

2f0; 1g8S 2 S : (4)

The linear programming (LP) relaxation is the same linear

program with constraints (4)replacedwithx

 0forall

S 2 S. The corresponding dual linear program is

min

e2E

i=1

(5)

s.t. z

e2S

(e)y

 c

8i 2f1;:::;kg8S 2 S

(6)

; y

 0 8i 2f1;:::;kg8e 2 E: (7)

Based on these LPs, Fig. 2 speciﬁes a primal-dual mecha-

nism for routing, called Greedy-1. Greedy-1 ensures feasi-

bility by using y

’s: if an added set exceeded the capacity b

of some e 2 E, then this would imply the stopping condi-

tion already in the previous iteration. Using the weak du-

ality of LPs the following result can be shown.

Theorem 3 Greedy-1 outputs a feasible solution, and it

is a (

e B

B1

(m)

1/(B1)

)-approximation algorithm if there is

a polynomial time algorithm that ﬁnds a  -approximate set

in line 4.

In case of UFP  = 1, as the shortest s

-t

-path computa-

tion ﬁnds set S

in line 4 of Greedy-1. For multicast rout-

ing, this problem corresponds to the NP-hard Steiner tree

problem, for which one can take  =1:55. Greedy-1 can

easily be shown to be monotone in demands and valua-

tions as required in Theorem 1. Thus it implies a truth-

ful mechanism for allocating network resources. The com-

modities correspond to bidders, the terminal nodes of bid-

ders are known, but the bidders might lie about their de-

mands and valuations. In the multicast routing the set of

terminals for each bidder is known but the demands and

valuations are unknown.

Corollary 1 Given any >0,B 1+, Greedy-1 is

atruthfulO(m

1/(B1)

)-approximation mechanism for UFP

(unicast routing) as well as for the multicast routing prob-

lem, where the demands and valuations of the bidders are

unknown.

When B is large, ˝(log m), then the approximation fac-

tor in Corollary 1 becomes constant. Azar et al. [4]pre-

sented further results in case of large B.Awerbuchetal.[3]

gave randomized online truthful mechanisms for uni-

and multicast routing, obtaining an expected O(log(m))-

approximation if B = ˝(log m), where  is the ratio of the

largest to smallest valuation. Their approximation holds

in fact with respect to the revenue of the auctioneer, but

they assume that the demands are known to the mecha-

nism. Bartal et al. [5] give a truthful O(B  (m/)

1/(B2)

approximation mechanism for UFP with unknown valua-

tions and demands, where  =min

Greedy-1 can be modiﬁed to give truthful mecha-

nisms for multi-unit CAs among unknown single-mined

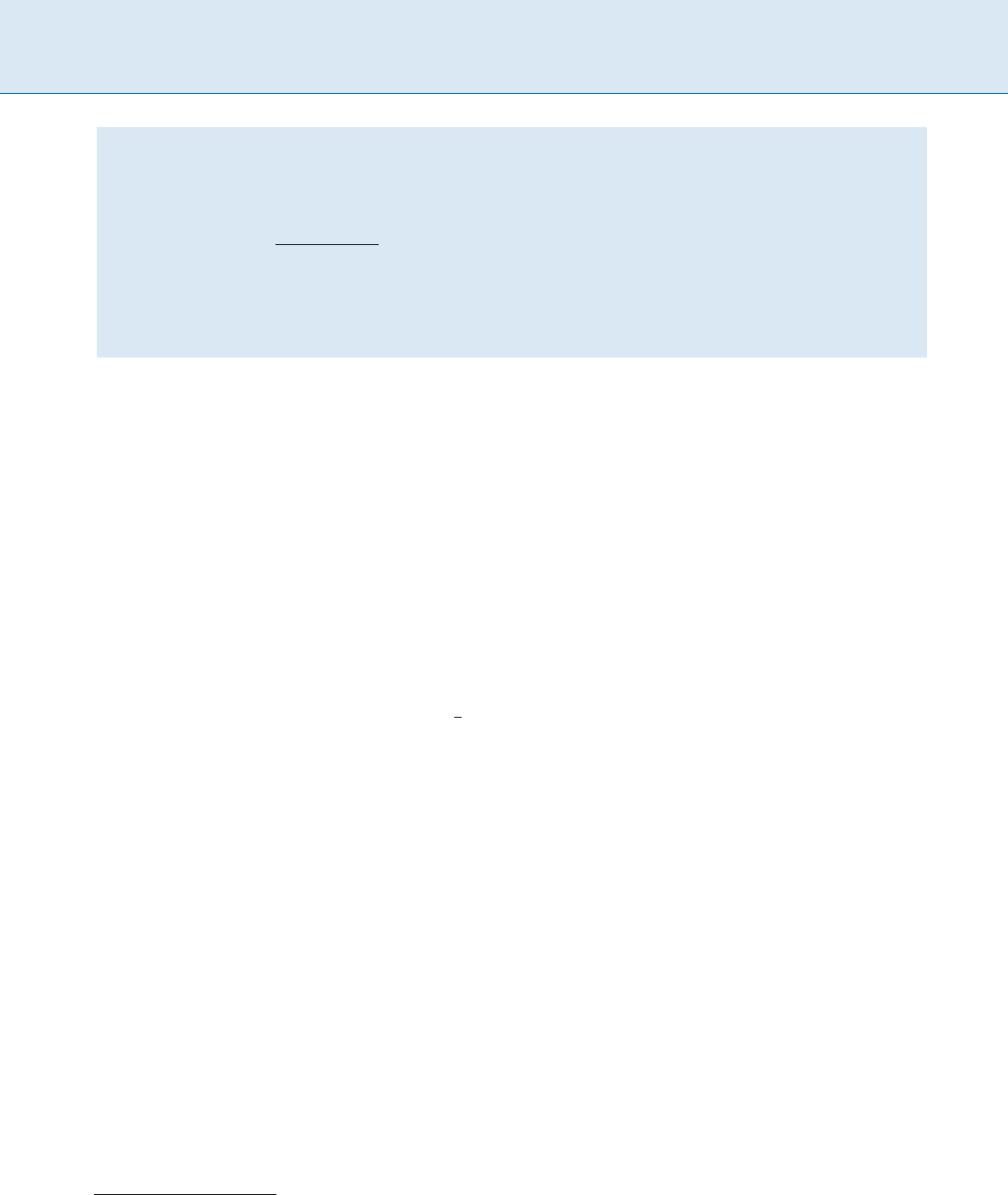
1000 U Utilitarian Mechanism Design for Single-Minded Agents

Algorithm Greedy-2:

T := ;;

2 forall e 2 U do y

:= 1/ b

;

3 repeat

4 S := argmax



e2U

(e)y

S 2 S n T



;

T := T [fSg;

6 forall e 2 S do y

:= y

(e

(e)/b

;

7 until

e2U

 e

8returnT.

Utilitarian Mechanism Design for Single-Minded Agents, Figure 3

Truthful mechanism for multi-unit CAs among unknown single-minded bidders. For CAs without multisets: q

(e) 2f0; 1g for each

e 2 U, S 2

bidders.

Archer et al. [2]usedrandomizedrounding

to obtain a truthful mechanism for multi-unit CAs, but

only in a probabilistic sense and only for known bidders.

Multi-unit CA among single-minded bidders is a special

case of ILP (1)–(4), where j

j =1 for each i 2 K,and

(e) 2f0; 1gfor each e 2 U, S 2 S (E is U in CAs). A bid

of bidder i 2 K is (a

; v

)=(S; c

), S 2 S

,andc

= c

the valuation. The relation R



is . Algorithm Greedy-2

in Fig. 3 is exact and monotone for CAs with unknown

single-minded bidders, as needed in Theorem 1.

Theorem 4 Algorithm Greedy-2 is a truthful O(m

)-ap-

proximation mechanism for multi-unit CAs among un-

known single-minded bidders.

Bartal et al. [5] presented a truthful mechanism for this

problem among unknown single-minded bidders which

is O(B  m

1/(B2)

)-approximate. (It works in fact for more

general bidders.)

Applications

Applications of the techniques described above are pre-

sented and a short survey of other results.

Applications of monotone approximation schemes

In a forward multi-unit auction a single auctioneer wants

to sell m identical items to n possible buyers (bidders).

Each single-minded bidder speciﬁes the number of items

she is interested in and a price she is willing to pay. El-

ements in the introduced notation correspond to the re-

quested and allocated numbers of items. Relation R



de-

Inthecaseofunknown single-minded bidders, the bidders have

as private data not only their valuations (as in the case of known

single-minded bidders) but also the sets they demand.

scribes that bidder i requesting q

items will be satis-

ﬁed also by any larger number of items. Mu’alem and

Nisan [11] give a 2-approximate monotone algorithm for

this problem. Theorem 2 gives a monotone FPTAS for

multi-unit auctions among unknown single-minded bid-

ders. This FPTAS is truthful with respect to agents where

both the number of items and price are private.

In job scheduling with deadlines (JSD),eachagenti

has a job with running time t

,deadlined

and a price

she is willing to pay if her job is processed by dead-

line d

.Elementa

is deﬁned as a

=(t

; d

). Output for

agent i is a time slot for processing i’s job. For two el-

ements a

=(t

; d

)anda

=(t

; d

)onehasa

 a

 t

and d

 d

. Theorem 2 leads to a monotone FP-

TAS, which, however, is not exact (see Theorem 1) with

respect to deadlines, and so it is a truthful mechanism

only if the deadlines are known. The techniques of The-

orem 2 apply also to minimization mechanism design

problems with a single buyer, such as reverse multi-unit

auctions, scheduling to minimize tardiness, constrained

shortest path and minimum spanning tree problems [6].

Applications of the primal dual algorithms

The applications of the primal dual algorithms are com-

binatorial auctions and auctions for unicast and multicast

routing. As these applications are tied very much to the al-

gorithms, they have already been presented in Sect. “Key

Results”.

Survey of other results

First truthful mechanisms for single-minded CAs were

the concept of single-minded agents, identiﬁed the role

of monotonicity, and used greedy algorithms to design

Utilitarian Mechanism Design for Single-Minded Agents U 1001

truthful mechanisms. Better approximation ratios of these

greedy mechanisms were proved by Krysta [9]withthe

help of LP duality. A tool-box of techniques for designing

truthful mechanisms for CAs was given by Mu’alem and

Nisan [11].

The previous section presented a monotone FPTAS

for job scheduling with deadlines where jobs are selﬁsh

agents and the seller oﬀers the agents the facilities to pro-

cess their jobs. Such scenarios when jobs are selﬁsh agents

to be scheduled on (possibly selﬁsh) machines have been

investigated further by Andelman and Mansour [1], see

also references therein.

So far social welfare was mostly assumed as the ob-

jective, but for a seller probably more important is to

maximize her revenue. This objective turns out to be

much harder to enforce in mechanism design. Such truth-

ful (in probabilistic sense) mechanisms were obtained for

auctioning unlimited supply goods among one-parameter

agents [7,8]. Another approach to maximizing seller’s rev-

enue is known as optimal auction design [12]. A seller

wants to auction a single good among agents and each

agent has a private value for winning the good. One

assumes that the seller knows a joint distribution of

those values and wants to maximize her expected rev-

enue [13,14].

Cross References

Mechanisms that approximately maximize revenue for

unlimited-supply goods as of Goldberg, Hartline and

Wright 8 are presented in entry  Competitive Auction.

Recommended Reading

1. Andelman, N., Mansour, Y.: A sufficient condition for truthful-

ness with single parameter agents. In: Proc. 8th ACM Confer-

ence on Electronic Commerce (EC),Ann, Arbor, Michigan, June

(2006)

2. Archer,A.,Papadimitriou,C.H.,Talwar,K.,Tardos,E.:Anapprox-

imate truthful mechanism for combinatorial auctions with sin-

gle parameter agents. In: Proc. 14th Ann. ACM–SIAM Symp. on

Discrete Algorithms (SODA), pp. 205–214. Baltimore, Maryland

(2003)

3. Awerbuch, B., Azar, Y., Meyerson, A.: Reducing truth-tellingon-

line mechanisms to online optimization. In: Proc. 35th Ann.

ACM. Symp. on Theory of Comput. (STOC), San Diego, Califor-

nia (2003)

4. Azar, Y., Gamzu, I., Gutner, S.: Truthful unsplittable flow for

large capacity networks. In: Proc. 19th Ann. ACM Symp. on Par-

allelism in Algorithms and Architectures (SPAA), pp. 320–329

(2007)

5.Bartal,Y.,Gonen,R.,Nisan,N.:Incentivecompatiblemulti

unit combinatorial auctions. In: Proceedings of the 9th con-

ference on Theoretical aspects of rationality and knowledge

(TARK), pp. 72–87. ACM Press (2003). http://doi.acm.org/10.

1145/846241.846250

6. Briest, P., Krysta, P., Vöcking, B.: Approximation techniques for

utilitarian mechanism design. In: Proc. 37th Ann. ACM. Symp.

on Theory of Comput. (STOC), pp. 39–48 (2005)

7. Fiat, A., Goldberg, A.V., Hartline, J.D., Karlin, A.R.: Competitive

generalized auctions. In: Proc. 34th Ann. ACM. Symp. on The-

ory of Comput. (STOC), pp. 72–81 (2002)

8. Goldberg, A.V., Hartline, J.D., Wright, A.: Competitive auctions

and digital goods. In: Proc. 12th Ann. ACM–SIAM Symp. on Dis-

crete Algorithms (SODA), pp. 735–744 (2001)

9. Krysta, P.: Greedy approximation via duality for packing, com-

binatorial auctions and routing. In: Proc. 30th Int. Confer-

ence on Mathematical Foundations of Comput. Sci. (MFCS).

Lecture Notes in Computer Science, vol. 3618, pp. 615–627

(2005)

10. Lehmann, D.J., O’Callaghan, L.I., Shoham, Y.: Truth revelation

in approximately efficient combinatorial auctions. In: Proc. 1st

ACM Conference on Electronic Commerce (EC), pp. 96–102

(1999)

11. Mu’alem, A., Nisan, N.: Truthful approximation mechanisms for

restricted combinatorial auctions. In: Proc. 18th Nat. Conf. Arti-

ficial Intelligence, pp. 379–384. AAAI (2002)

12. Myerson, R.B.: Optimal auction design. Math. Oper. Res. 6,

58–73 (1981)

13. Ronen, A.: On approximating optimal auctions (extended ab-

stract). In: Proc. 3rd ACM Conference on Electronic Commerce

(EC), pp. 11–17 (2001)

14. Ronen, A., Saberi, A.: On the hardness of optimal auctions. In:

Proc. 43rd Ann. IEEE Symp. on Foundations of Comput. Sci.

(FOCS), pp. 396–405 (2002)

Vertex Cover Kernelization V 1003

Valid-Utility Games

 Market Games and Content Distribution

VCG

 Generalized Vickrey Auction

Vector Sorting

 String Sorting

Vertex Coloring

 Distributed Vertex Coloring

 Exact Graph Coloring Using Inclusion–Exclusion

Vertex Cover Data Reduction

 Vertex Cover Kernelization

Vertex Cover Kernelization

2004; Abu-Khzam, Collins, Fellows, Langston,

Suters, Symons

JIANER CHEN

Department of Computer Science,

Texas A&M University, College Station, TX, USA

Keywords and Synonyms

Vertex cover preprocessing; Vertex cover data reduction

Problem Definition

Let G be an undirected graph. A subset C of vertices in G is

a vertex cover for G if every edge in G has at least one end in

C. The (parametrized)

VERTEX COVER problem is for each

given instance (G, k), where G is a graph and k  0isan

integer (the parameter), to determine whether the graph G

has a vertex cover of at most k vertices.

The

VERTEX COVER problem is one of the six “ba-

sic” NP-complete problems according to Garey and John-

son [4]. Therefore, the problem cannot be solved in

polynomial time unless P = NP. However, the NP-

completeness of the problem does not obviate the need

for solving it because of its fundamental importance and

wide applications. One approach was initiated based on

the observation that in many applications, the parameter

k is small. Therefore, by taking the advantages of this fact,

one may be able to solve this NP-complete problem eﬀec-

tively and practically for instances with a small parameter.

More speciﬁcally, algorithms of running time of the form

f (k)p(n) have been studied for

VERTEX COVER,where

p(n) is a low-degree polynomial of the number n = jGj of

vertices in G and f (k) is a function independent of n.

There has been an impressive sequence of improved

algorithms for the

VERTEX COVER problem. A number of

new techniques have been developed during this research,

including kernelization, folding, and reﬁned branch-and-

search. In particular, the kernelization method is the

study of polynomial time algorithms that can signiﬁ-

cantly reduce the instance size for

VERTEX COVER.The

following are some concepts related to the kernelization

method:

Deﬁnition 1 Two instances (G, k)and(G

; k

)ofVERTEX

COVER

are equivalent if the graph G has a vertex cover of

size  k if and only if the graph G

has a vertex cover of

size  k

Deﬁnition 2 A kernelization algorithm for the

VER-

TEX COVER problem takes an instance (G, k)ofVER-

TEX COVER as input and produces an equivalent instance

; k

)fortheproblem,suchthatjG

jjGj and k

 k.

1004 V Vertex Cover Kernelization

The kernelization method has been used extensively in

conjunction with other techniques in the development of

algorithms for the

VERTEX COVER problem. Two major

issues in the study of kernelization method are (1) eﬀec-

tive reductions of instance size; and (2) the eﬃciency of

kernelization algorithms.

Key Results

A number of kernelization techniques are discussed and

studied in the current paper.

Preprocessing Based on Vertex Degrees

Let (G, k) be an instance of

VERTEX COVER.Letv be a ver-

tex of degree larger than k in G. If a vertex cover C does not

include v,thenC must contain all neighbors of v,which

implies that C contains more than k vertices. Therefore, in

order to ﬁnd a vertex cover of no more than k vertices, one

must include v in the vertex cover, and recursively look for

a vertex cover of k  1 vertices in the remaining graph.

The following fact was observed on vertices of degree

less than 3.

Theorem 1 There is a linear time kernelization algorithm

that on each instance (G, k) of

VERTEX COVER,wherethe

graph G contains a vertex of degree less than 3, produces

an equivalent instance (G

; k

) such that jG

j < jGj and/or

k < k

Therefore, vertices of high degree (i. e., degree > k)and

low degree (i. e., degree < 3) can always be handled eﬃ-

ciently before any more time-consuming process.

Nemhauser-Trotter Theorem

Let G be a graph with vertices v

, v

, :::, v

.Considerthe

following integer programming problem:

(IP) Minimize x

+ x

+ + x

Subject to x

+ x

 1 for each edge [v

; v

]inG

2f0; 1g; 1  i  n

It is easy to see that there is a one-to-one correspondence

between the set of feasible solutions to (IP) and the set of

vertex covers of the graph G. A natural LP-relaxation (LP)

of the problem (IP) is to replace the restrictions x

2f0; 1g

with x

 0foralli. Note that the resulting linear pro-

gramming problem (LP) now can be solved in polynomial

time.

Let  = fx

;:::;x

g be an optimal solution to the

linear programming problem (LP). The vertices in the

graph G can be partitioned into three disjoint parts accord-

ing to :

= fv

j x

< 0:5g;

= fv

j x

> 0:5g; and

= fv

j x

=0:5g

The following nice property of the above vertex partition

of the graph G was ﬁrst observed by Nemhauser and Trot-

ter [5].

Theorem 2 (Nemhauser-Trotter) Let G[V

] be the sub-

graph of G induced by the vertex set V

. Then (1) every

vertex cover of G[V

] contains at least jV

j/2 vertices; and

(2) every minimum vertex cover of G[V

] plus the vertex set

makes a minimum vertex cover of the graph G.

Let k be any integer, and let G

= G[V

]andk

= k jC

As ﬁrst noted in [3], by Theorem 2, the instances (G, k)

and (G

; k

) are equivalent, and jG

j2k

is a necessary

condition for the graph G

to have a vertex cover of size

. This observation gives the following kernelization re-

sult.

Theorem 3 There is a polynomial-time algorithm that for

a given instance (G, k) for the

VERTEX COVER problem,

constructs an equivalent instance (G

; k

) such that k

 k

and jG

j2k

A faster Nemhauser-Trotter Construction

Theorem 3 suggests a polynomial-time kernelization algo-

rithm for

VERTEX COVER. The algorithm is involved in

solving the linear programming problem (LP) and parti-

tioning the graph vertices into the sets I

, C

,andV

.Solv-

ing the linear programming problem (LP) can be done in

polynomial time but is kind of costly in particular when

the input graph G is dense. Alternatively, Nemhauser and

Trotter [5] suggested the following algorithm without us-

ing linear programming. Let G be the input graph with

vertex set fv

;:::;v

1. construct a bipartite graph B with vertex set fv

;:::;

; v

;:::;v

g such that [v

; v

]isanedgeinB if and

only if [v

; v

]isanedgeinG;

2. ﬁnd a minimum vertex cover C

for B;

3. I

= fv

j if neither v

nor v

is in C

= fv

j if both v

and v

are in C

= fv

j if exactly one of v

and v

is in C

It can be proved [5](seealso[2]) that Theorem 2 still

holds true when the sets C

and V

in the theorem are re-

placed by the sets C

and V

, respectively, constructed in

the above algorithm.

Vertex Cover Kernelization V 1005

The advantage of this approach is that the sets C

and

can be constructed in time O(m

n) because the mini-

mum vertex cover C

for the bipartite graph B can be con-

structed via a maximum matching of B, which can be con-

structed in time O(m

n) using Dinic’s maximum ﬂow al-

gorithm, which is in general faster than solving the linear

programming problem (LP).

Crown Reduction

For a set S of vertices in a graph G,denotebyN(S)thesetof

vertices that are not in S but adjacent to some vertices in S.

A crown in a graph G is a pair (I, H) of subsets of vertices

in G satisfying the following conditions: (1) I ¤;is an

independent set, and H = N(I); and (2) there is a matching

M on the edges connecting I and H such that all vertices

in H are matched in M.

It is quite easy to see that for a given crown (I, H),

there is a minimum vertex cover that includes all vertices

in H and excludes all vertices in I.LetG

be the graph

obtained by removing all vertices in I and H from G.

Then, the instances (G, k)and(G

; k

) are equivalent,

where k

= k jHj. Therefore, identiﬁcation of crowns in

a graph provides an eﬀective way for kernelization.

Let G be the input graph. The following algorithm is

proposed.

1. construct a maximal matching M

in G;letO be the set

of vertices unmatched in M

;

2. construct a maximum matching M

of the edges be-

tween O and N(O); i =0; letI

be the set of vertices

in O that are unmatched in M

;

3. repeat until I

= I

i1

= N(I

); I

i+1

= I

[ N

);

i = i +1;};(whereN

) is the set of vertices in O

that match the vertices in H

in the matching M

)

4. I = I

; H = N(I

); output (I, H).

Theorem 4 (1) if the set I

is not empty, then the above

algorithm constructs a crown (I, H); (2) if both jM

j and

jare bounded by k, and I

= ;, then the graph G has at

most 3k vertices.

According to Theorem 4, the above algorithm on an in-

stance (G, k)of

VERTEX COVER either (1) ﬁnds a match-

ing of size larger than k – which implies that there is no

vertex cover of k vertices in the graph G; or (2) constructs

acrown(I, H) – which will reduce the size of the instance;

or (3) in case neither of (1) and (2) holds true, concludes

that the graph G contains at most 3k vertices. Therefore,

repeatedly applying the algorithm either derives a direct

solution to the given instance, or constructs an equivalent

instance (G

; k

)withk

 k and jG

j3k

Applications

The research of the current paper was directly motivated

by authors’ research in bioinformatics. It is shown that for

many computational biological problems, such as the con-

struction of phylogenetic trees, phenotype identiﬁcation,

and analysis of microarray data, preprocessing based on

the kernelization techniques has been very eﬀective.

Experimental Resul t s

Experimental results are given for handling graphs ob-

tained from the study of phylogenetic trees based on pro-

tein domains, and from the analysis of microarray data.

The results show that in most cases the best way to ker-

nelize is to start handling vertices of high and low de-

grees (i. e., vertices of degree larger than k or smaller than

3) before attempting any of the other kernelization tech-

niques. Sometimes, kernelization based on Nemhauser-

Trotter Theorem can solve the problem without any fur-

ther branching. It is also observed that sometimes partic-

ularly on dense graphs, kernelization techniques based on

Nemhauser-Trotter Theorem are kind of time-consuming

but do not reduce the instance size by much. On the other

hand, the techniques based on high-degree vertices and

crown reduction seem to work better.

Data Sets

The experiments were performed on graphs obtained

based on data from NCBI and SWISS-PROT, well known

open-source repositories of biological data.

Cross References

 Data Reduction for Domination in Graphs

 Local Approximation of Covering and Packing

Problems

 Vertex Cover Search Trees

Recommended Reading

1. Abu-Khzam, F., Collins, R., Fellows, M., Langston, M., Suters, W.,

Symons, C.: Kernelization algorithms for the vertex cover prob-

lem: theory and experiments. In: Proc. Workshop on Algorithm

Engineering and Experiments (ALENEX) pp. 62–69 (2004)

2. Bar-Yehuda, R., Even, S.: A local-ratio theorem for approximat-

ing the weighted vertex cover problem. Ann. Discret. Math. 25,

27–45 (1985)

3. Chen, J., Kanj, I.A., Jia, W.: Vertex cover: further observations

and further improvements. J. Algorithm 41, 280–301 (2001)

4. Garey, M., Johnson, D.: Computers and Intractability: A Guide

to the Theory of NP-completeness. Freeman, San Francisco

(1979)

5. Nemhauser, G.L., Trotter, L.E.: Vertex packing: structural prop-

erties and algorithms. Math. Program. 8, 232–248 (1975)

1006 V Vertex Cover Preprocessing

Vertex Cover Preprocessing

 Vertex Cover Kernelization

Vertex Cover Search Trees

2001; Chen, Kanj, Jia

JIANER CHEN

Department of Computer Science, Texas A&M

University, College Station, TX, USA

Keywords and Synonyms

Branch and search; Branch and bound

Problem Definition

The

VERTEX COVER problem is one of the six “basic” NP-

complete problems according to Garey and Johnson [7].

Therefore, the problem cannot be solved in polynomial

time unless P = NP. However, the NP-completeness of the

problem does not obviate the need for solving it because of

its fundamental importance and wide applications.

One approach is to develop parameterized algorithms

for the problem, with the computational complexity of the

algorithms being measured in terms of both input size and

a parameter value. This approach was initiated based on

the observation that in many applications, the instances of

the problem are associated with a small parameter. There-

fore, by taking the advantages of the small parameters, one

may be able to solve this NP-complete problem eﬀectively

and practically.

The problem is formally deﬁned as follows. Let G be an

(undirected) graph. A subset C of vertices in G is a vertex

cover for G if every edge in G has at least one end in C.

An instance of the (parameterized)

VERTEX COVER prob-

lem consists of a pair (G, k), where G is a graph and k is

an integer (the parameter), which is to determine whether

the graph G has a vertex cover of k vertices. The goal

is to develop parameterized algorithms of running time

O(f (k)p(n)) for the

VERTEX COVER problem, where p(n)

is a lower-degree polynomial of the input size n,andf (k)

is the non-polynomial part that is a function of the param-

eter k but independent of the input size n.Itwouldbeex-

pected that the non-polynomial function f (k)isassmall

as possible. Such an algorithm would become “practically

eﬀective” when the parameter value k is small. It should be

pointed out that unless an unlikely consequence occurs in

complexity theory, the function f (k) is at least an exponen-

tial function of the parameter k [8].

Key Results

A number of techniques have been proposed in the de-

velopment of parameterized algorithms for the

VERTEX

COVER

problem.

Kernelization

Suppose (G, k) is an instance for the

VERTEX COVER prob-

lem, where G is a graph and k is the parameter. The ker-

nelization operation applies a polynomial time prepro-

cessing on the instance (G, k) to construct another in-

stance (G

, k

), where G

is a smaller graph (the kernel)and

 k,suchthatG

has a vertex cover of k

vertices if and

only if G has a vertex cover of k vertices. Based on a clas-

sical result by Nemhauser and Trotter [9], the following

kernelization result was derived.

Theorem 1 There is an algorithm of running time

O(kn + k

) that for a given instance (G, k) for the VERTEX

COVER

problem, constructs another instance (G

)forthe

problem, where the graph G

contains at most 2k

vertices

and k

 k, such that the graph G has a vertex cover of k

vertices if and only if the graph G

has a vertex cover of k

vertices.

Therefore, kernelization provides an eﬃcient preprocess-

ing for the

VERTEX COVER problem, which allows one to

concentrate on graphs of small size (i. e., graphs whose size

is only related to k).

Folding

Suppose v is a degree-2 vertex in a graph G with two neigh-

bors u and w such that u and w are not adjacent to each

other. Construct a new graph G

as follows: remove the

vertices v, u,andw and introduce a new vertex v

that is

adjacent to all remaining neighbors of the vertices u and w

in G.ThegraphG

is said being obtained from the graph

G by folding the vertex v. The following result was derived.

Theorem 2 Let G

be a graph obtained by folding a degree-

2 vertex v in a graph G, where the two neighbors of v are not

adjacent to each other. Then the graph G has a vertex cover

of k vertices if and only if the graph G

has a vertex cover of

k 1 vertices.

An folding operation allows one to decrease the value of

the parameter k without branching. Therefore, folding op-

erations are regarded as very eﬃcient in the development

of exponential time algorithms for the

VERTEX COVER

problem. Recently, the folding operation has be general-

ized to apply to a set of more than one vertex in a graph [6].

Vertex Cover Search Trees V 1007

Branch and Search

A main technique is the branch and search method that has

been extensively used in the development of algorithms

for the

VERTEX COVER problem (and for many other NP-

hard problems). The method can be described as follows.

Let (G; k) be an instance of the

VERTEX COVER problem.

Suppose that somehow a collection fC

;:::;C

gof vertex

subsets in the graph G is identiﬁed, where for each i,the

subset C

has c

vertices, such that if the graph G contains

a vertex cover of k vertices, then at least for one C

of the

vertex subsets in the collection, there is a vertex cover of k

vertices for G that contains all vertices in C

.Thenacol-

lection of (smaller) instances (G

, k

) can be constructed,

where 1  i  b; k

= k  c

,andG

is obtained from G

by removing all vertices in C

. Note that the original graph

G has a vertex cover of k vertices if and only if for one

, k

) of the smaller instances the graph G

has a ver-

tex cover of k

vertices. Therefore, now the process can be

branched into b sub-processes, each on a smaller instance

, k

) recursively searches for a vertex cover of k

vertices

in the graph G

Let T(k) be the number of leaves in the search tree for

the above branch and search process on the instance (G, k),

then the above branch operation gives the following recur-

rence relation:

T(k)=T(k  c

)+T(k  c

)++ T(k  c

)

To solve this recurrence relation, let T(k)=x

so that the

above recurrence relation becomes

= x

kc

+ x

kc

+ + x

kc

It can be proved [3] that the above polynomial equation

has a unique root x

larger than 1. From this, one gets

T(k)=x

,which,uptoapolynomialfactor,givesanup-

per bound on the running time of the branch and search

process on the instance (G, k).

The simplest case is that a vertex v of degree d > 0in

the graph G is picked. Let w

,...,w

be the neighbors of v.

Then either v is contained in a vertex cover C of k vertices,

or, if v is not contained in C, then all neighbors w

,...,w

of v must be contained in C. Therefore, one obtains a col-

lection of two subsets C

= fvgand C

= fw

;:::;w

g,on

which the branch and search process can be applied.

The eﬃciency of a branch and search operation de-

pends on how eﬀectively one can identify the collection

of the vertex subsets. Intuitively, the larger the sizes of the

vertex subsets, the more eﬃcient is the operation. Much ef-

fort has been made in the development of

VERTEX COVER

algorithms to achieve larger vertex subsets. Improvements

on the size of the vertex subsets have been involved with

very complicated and tedious analysis and enumerations

of combinatorial structures of graphs. The current pa-

per [3] achieved a collection of two subsets C

and C

sizes c

=1andc

= 6, respectively, and other collections

of vertex subsets that are at least as good as this (the tech-

niques of kernelization and vertex folding played impor-

tant roles in achieving these collections). This gives the fol-

lowing algorithm for the

VERTEX COVER problem.

Theorem 3 The

VERTEX COVER problem can be solved in

time O(kn +1:2852

Very recently, a further improvement over Theorem 3 has

been achieved that gives an algorithm of running time

O(kn +1:2738

)fortheVERTEX COVER problem [4].

Applications

The study of parameterized algorithms for the

VERTEX

COVER

problem was motivated by ETH Zürich’s DAR-

WIN project in computational biology and computational

biochemistry (see, e. g. [10,11],). A number of computa-

tional problems in the project, such as multiple sequence

alignments [10] and biological conﬂict resolving [11], can

be formulated into the

VERTEX COVER problem in which

the parameter value is in general not larger than 100.

Therefore, an algorithm of running time O(kn +1:2852

)

for the problem becomes very eﬀective and practical in

solving these problems.

The parameterized algorithm given in Theorem 3 has

also induced a faster algorithm for another important NP-

hard problem, the

MAXIMUM INDEPENDENT SET prob-

lem on sparse graphs [3].

Open Problems

The main open problem in this line of research is how

far one can go along this direction. More speciﬁcally, how

small the constant c > 1canbeforthe

VERTEX COVER

problem to have an algorithm of running time O(c

O(1)

With further more careful analysis on graph combinatorial

structures, it seems possible to slightly improve the cur-

rent best upper bound [4] for the problem. Some new tech-

niques developed more recently [6] also seem very promis-

ing to improve the upper bound. On the other hand, it is

known that the constant c cannot be arbitrarily close to 1

unless certain unlikely consequence occurs in complexity

theory [8].

Experimental Resul t s

A number of research groups have implemented some of

the ideas of the algorithm in Theorem 3 or its variations,