Kao M.-Y. (ed.) Encyclopedia of Algorithms

Подождите немного. Документ загружается.

988 T Two-Interval Pattern Problems

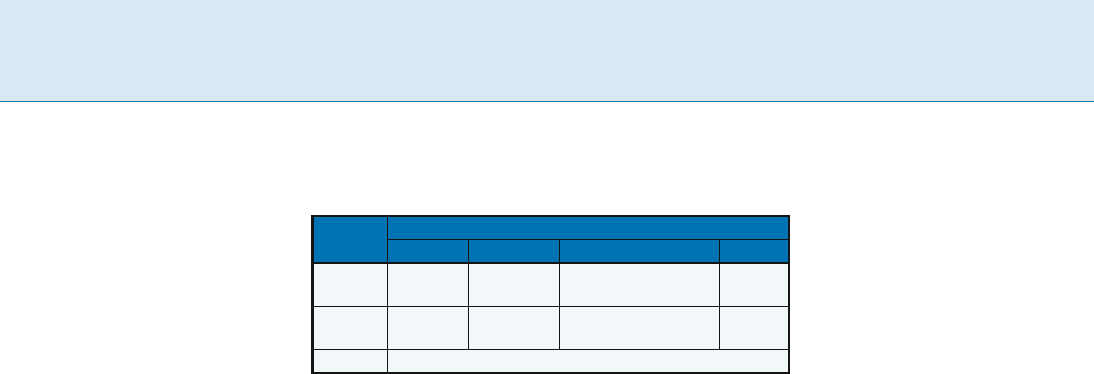
Two-Interval Pattern Problems, Table 2

Performance ratios for hard instances of the 2-interval-pattern problem. LP stands for Linear Programming and N/A stands for Not

Applicable

Model R

Interval ground set I(D)

Unlimited Balanced Unit Disjoint

f<; @;Gg 4LP[1] 4

O(n lg n)[7]

2+

O(n

+ n

O(log 1/)

)[13]

N/A

f@;Gg 4LP[7] 4

O(n

lg n)[7]

2+

O(n

+ n

O(log 1/)

)[13]

N/A

f<;Gg 1+1/ O(n

2+3

); 2[14]

Open Problems

A number of problems related to the 2-interval-pattern

problem remain open. First, improving the approxima-

tion ratios for the various ﬂavors of the 2-interval-pattern

problem is of particular importance. For example, the exis-

tence of a fast approximation algorithm with good perfor-

mance guarantee for the 2-interval-pattern problem for

model

R = f<; @;Gg remains an apparently challenging

open problem. A related open research area is concerned

with balanced-interval ground sets. In particular, no ev-

idence has shown yet that the 2-interval-pattern prob-

lem becomes easier to approximate for balanced-interval

ground sets. This question is of special importance in the

context of RNA structures where most 2-intervals are bal-

anced.

A number of important question are still open for

model

R = f<;Gg. First, it is still unknown whether the

2-interval-pattern problem for disjoint-interval ground

sets and model

R = f<;Gg is polynomial-time-solvable.

Observe that this problem trivially reduces to the fol-

lowing graph problem: Given a graph G =(V; E)with

V = f1; 2;:::;ng, ﬁnd a maximum cardinality matching

M  E such that for any two distinct edges fi; jg and

fk; lg of

M, i < j, k < l and i < k,eitherj < k or j < l.

Another open question concerns the approximation of the

2-interval-pattern problem for balanced interval ground

set. Is this special case better approximable than the gen-

eral case?

A last direction of research is concerned with the pa-

rameterized complexity of the 2-interval-pattern prob-

lem. For example, it is not known whether the 2-interval-

pattern problem for models

R = f<; @;Gg, R = f@;Gg or

R = f<;Gg is ﬁxed-parameter-tractable when parameter-

ized by the size of the solution. Also, investigating the pa-

rameterized complexity for parameters such as the max-

imum number of pairwise crossing intervals in the input

set or the treewidth of the corresponding intersection 2-in-

terval graph, which are expected to be relatively small for

most practical applications, is of particular interest.

Cross References

 RNA Secondary Structure Prediction Including

Pseudoknots

 RNA Secondary Structure Prediction by Minimum

Free Energy

Recommended Reading

1. Bar-Yehuda, R., Halldorsson, M., Naor, J., Shachnai, H., Shapira,

I.: Scheduling split intervals. In: Proc. 13th Annual ACM-SIAM

Symposium on Discrete Algorithms (SODA), 2002, pp. 732–741

2. Billoud, B., Kontic, M., Viari, A.: Palingol a declarative program-

ming language to describe nucleic acids’ secondary structures

and to scan sequence database. Nucleic. Acids. Res. 24, 1395–

1403 (1996)

3. Blin, G., Fertin, G., Vialette, S.: Extracting 2-intervals subsets

from 2-interval sets. Theor. Comput. Sci. 385(1–3), 241–263

(2007)

4. Blin, G., Fertin, G., Vialette, S.: New results for the 2-interval pat-

tern problem. In: Proc. 15th Annual Symposium on Combina-

torial Pattern Matching (CPM). Lecture Notes in Computer Sci-

ence, vol. 3109. Springer, Berlin (2004)

5. Butman, A., Hermelin, D., Lewenstein, M., Rawitz, D.: Optimiza-

tion problems in multiple-interval graphs. In: Proc. 9th Annual

ACM-SIAM Symposium on Discrete Algorithms (SODA), ACM-

SIAM, 2007, pp. 268–277

6. Chen, J.-H., Le, S.-Y., Maize, J.: Prediction of common secondary

structures of RNAs: a genetic algorithm approach. Nucleic.

Acids. Res. 28, 991–999 (2000)

7. Crochemore,M.,Hermelin,D.,Landau,G.,Rawitz,D.,Vialette,

S.: Approximating the 2-interval pattern problem, Theoretical

Computer Science (special issue for Alberto Apostolico) (2008)

8. Erdong, C., Linji, Y., Hao, Y.: Improved algorithms for 2-interval

pattern problem. J. Combin. Optim. 13(3), 263–275 (2007)

9. Halldorsson, M., Karlsson, R.: Strip graphs: Recognition and

scheduling. In: Proc. 32nd International Workshop on Graph-

Theoretic Concepts in Computer Science (WG). Lecture Notes

in Computer Science, vol. 4271, pp. 137–146. Springer, Berlin

(2006)

10. Jiang, M.: A 2-approximation for the preceding-and-crossing

structured 2-interval pattern problem, J. Combin. Optim. 13,

217–221 (2007)

11. Jiang, M.: Improved approximation algorithms for predicting

RNA secondary structures with arbitrary pseudoknots. In: Proc.

3rd International Conference on Algorithmic Aspects in Infor-

Two-Level Boolean Minimization T 989

mation and Management (AAIM), Portland, OR, USA, Lecture

Notes in Computer Science, vol. 4508, pp. 399–410. Springer

(2007)

12. Jiang, M.: A PTAS for the weighted 2-interval pattern problem

over the preceding-and-crossing model. In: Y.X. A.W.M. Dress,

B. Zhu (eds.) Proc. 1st Annual International Conference on

Combinatorial Optimization and Applications (COCOA), Xi’an,

China, Lecture Notes in Computer Science, vol. 4616, pp. 378–

387. Springer (2007)

13. Joseph, D., Meidanis, J., Tiwari, P.: Determining DNA sequence

similarity using maximum independent set algorithms for in-

terval graphs. In: Proc. 3rd Scandinavian Workshop on Al-

gorithm Theory (SWAT). Lecture Notes in Computer Science,

pp. 326–337. Springer, Berlin (1992)

14. Lyngsø, R., Pedersen, C.: RNA pseudoknot prediction in energy-

based models. J. Comput. Biol. 7, 409–427 (2000)

15. Micali,S.,Vazirani,V..AnO



sqrtjVjjEj



algorithm for finding

maximum matching in general graphs. In: Proc. 21st Annual

Symposium on Foundation of Computer Science (FOCS), IEEE,

1980, pp. 17–27

16. Nussinov,R.,Pieczenik,G.,Griggs,J.,Kleitman,D.:Algorithms

for loop matchings. SIAM J. Appl. Math. 35, 68–82 (1978)

17. Ren, J., Rastegart, B., Condon, A., Hoos, H.: HotKnots: Heuristic

prediction of rna secondary structure including pseudoknots.

RNA 11, 1194–1504 (2005)

18. Rivas, E., Eddy, S.: A dynamic programming algorithm for RNA

structure prediction including pseudoknots. J. Mol. Biol. 285,

2053–2068 (1999)

19. Ruan, J., Stormo, G., Zhang, W.: An iterated loop matching ap-

proach to the prediction of RNA secondary structures with

pseudoknots. Bioinformatics 20, 58–66 (2004)

20. Vialette, S.: On the computational complexity of 2-interval pat-

tern matching. Theor. Comput. Sci. 312, 223–249 (2004)

21. Zhao, J., Malmberg, R., Cai, L.: Rapid ab initio rna folding includ-

ing pseudoknots via graph tree decomposition. In: Proc. Work-

shop on Algorithms in Bioinformatics. Lecture Notes in Com-

puter Science, vol. 4175, pp. 262–273. Springer, Berlin (2006)

Two-Level Boolean Minimization

1956; McCluskey

ROBERT DICK

Department Electrical Engineering and Computer

Systems, Northwestern University, Evanston, IL, USA

Keywords and Synonyms

Logic minimization; Quine–McCluskey algorithm; Tabu-

lar method

Problem Definition

Summary

Find a minimal sum-of-products expression for a Boolean

function.

Two-Level Boolean Minimization, Table 1

Equivalent representations with different implementation com-

plexities

Expression Meaning in english Boolean logic

identity

a ^b _a ^b not a and not b or not a and b

Distributivity

Complements

Boundedness

a ^



b _b



not a and either not b or b

a ^True not a and True

a not a

Extended Deﬁnition

Consider a Boolean algebra with two elements: False or

True. A Boolean function f (y

; y

; ; y

)ofn Boolean

input variables speciﬁes an output value for each combi-

nation of input variable values. It is possible to represent

the same function with a number of diﬀerent expressions.

For example, the ﬁrst and last expressions in Table 1 corre-

spond to this function. Assuming access to complemented

input variables, straight-forward implementations of these

expressions would require two and gates and an or gate for

a ^ b _ a ^ b and only a wire for a. Although the imple-

mentation eﬃciency depends on target technology, in gen-

eral terser expressions enable greater eﬃciency. Boolean

minimization is the task of deriving the tersest expression

for a function. Elegant and optimal algorithms exist for

solving the variant of this problem in which the expression

is limited to two levels, i. e., a layer of and gates followed

by a single or gate or a layer of or gates followed by a single

and gate.

Key Results

This survey will start by introducing the Karnaugh Map

visualization technique, which will be used to assist in

the subsequent explanation of the Quine–McCluskey algo-

rithm for two-level Boolean minimization. This algorithm

is optimal for its constrained problem variant. It is one of

the fundamental algorithms in the ﬁeld of computer-aided

design and forms the basis or inspiration for many solu-

tions to more general variants of the Boolean minimiza-

tion problem.

Karnaugh Maps

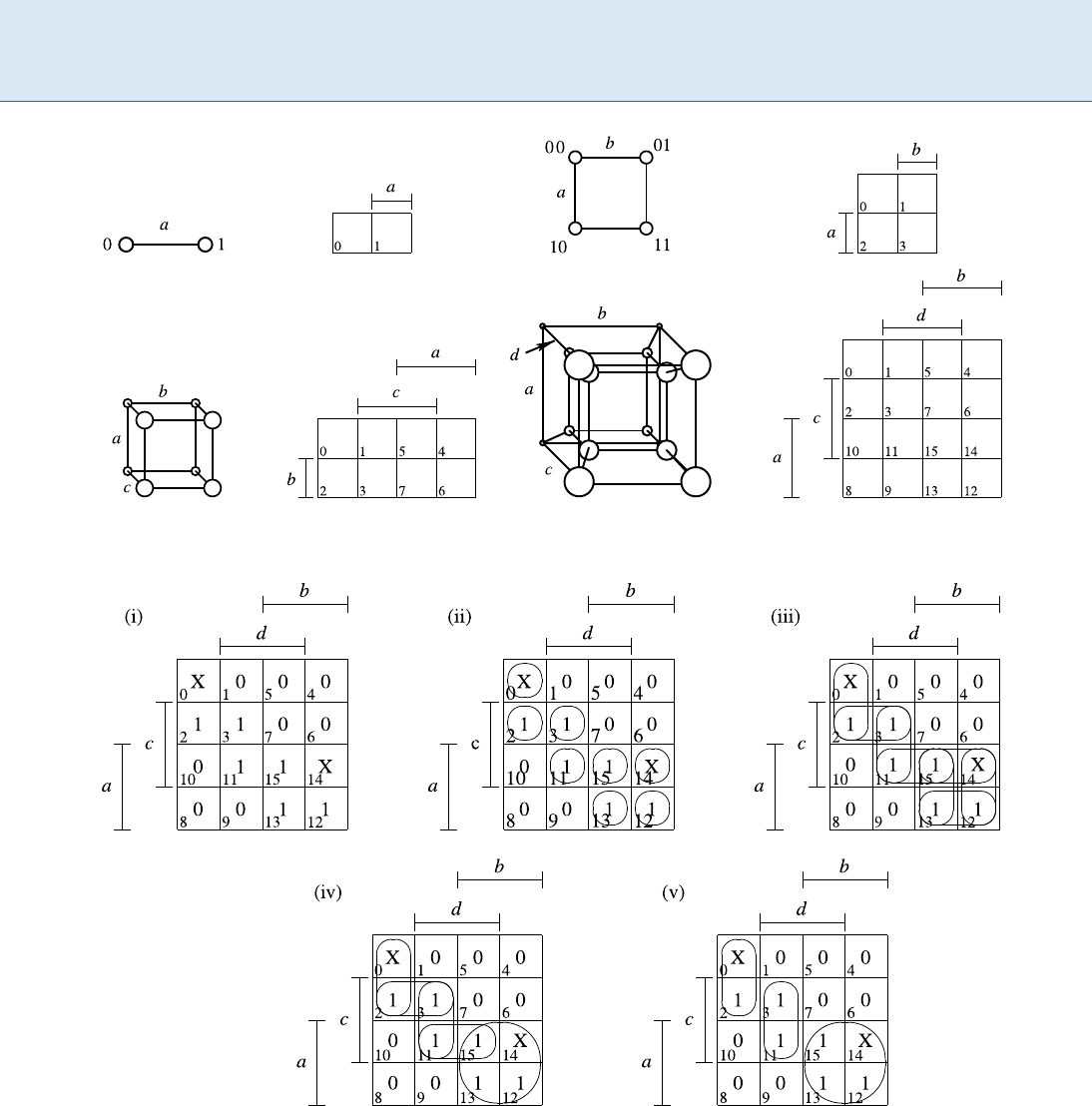
Karnaugh Maps [4] provide a method of visualizing adja-

cency in Boolean space. A Karnaugh Map is a projection of

an n-dimensional hypercube onto two-dimensional sur-

face such that adjacent points in the hypercube remain ad-

jacent in the two-dimensional projection. Figure 1 illus-

trates Karnaugh Maps of 1, 2, 3, and 4 variables: a, b, c,

and d.

990 T Two-Level Boolean Minimization

Two-Level Boolean Minimization, Figure 1

Boolean function spaces from one to four dimensions and their corresponding Karnaugh Maps

Two-Level Boolean Minimization, Figure 2

(i) Karnaugh Map of function f (a; b; c; d), (ii) elementary implicants, (iii) second-order implicants, (iv) prime implicants, and (v) a min-

imal cover

A literal is a single appearance of a complemented or

uncomplemented input variable in a Boolean expression.

A product term or implicant is the Boolean product, or

and, of one or more literals. Every implicant corresponds

to a repeated balanced bisection of Boolean space, or of the

corresponding Karnaugh Map, i. e., an implicant is a rect-

angle in a Karnaugh Map with width m and height n where

m =2

and n =2

for arbitrary non-negative integers j

and k,e.g,theovalsinFig.2(ii–v). An elementary impli-

cant is an implicant in which, for each variable of the cor-

Two-Level Boolean Minimization T 991

responding function, the variable or its complement ap-

pears, e. g., the circles in Fig. 2(ii). Implicant Acoversim-

plicant B if every elementary implicant in B is also in A.

Prime implicants are implicants that are not covered by

any other implicants, e. g., the ovals and circle in Fig. 2(iv).

It is unnecessary to consider anything but prime impli-

cants when seeking a minimal function representation be-

cause, if a non-prime implicants could be used to cover

some set of elementary implicants, there is guaranteed to

exist a prime implicant that covers those elementaryimpli-

cants and contains fewer literals. One can draw the largest

implicants covering each elementary implicant and cover-

ing no positions for which the function is False,thereby

using Karnaugh Maps to identify prime implicants. One

can then manually seek a compact subset of prime impli-

cants covering all elementary implicants in the function.

This Karnaugh Map based approach is eﬀective for

functions with few inputs, i. e., those with low dimen-

sionality. However, representing and manipulating Kar-

naugh Maps for functions of many variables is challenging.

Moreover, the Karnaugh Map method provides no clear

set of rules to follow when selecting a minimal subset of

prime implicants to implement a function.

The Quine–McCluskey Algorithm

The Quine–McCluskey algorithm provides a formal, op-

timal way of solving the two-level Boolean minimiza-

tion problem. W. V. Quine laid the essential theoret-

ical groundwork for optimal two-level logic minimiza-

tion [7,8]. However, E. J. McCluskey ﬁrst proposed a pre-

cise algorithm to fully automate the process [6].

The Quine–McCluskey method has two phases:

(1) produce all prime implicants and (2) select a minimal

subset of prime implicants covering the function. In the

ﬁrst phase, the elementary implicants of a function are it-

eratively combined to produce implicants with fewer lit-

erals. Eventually, all prime implicants are thus produced.

In the second phase, a minimal subset of prime implicants

covering the on-set elementary implicants is selected using

unate covering.

The Quine–McCluskey method may be illustrated us-

ing an example. Consider the function indicated by the

Karnaugh Map in Fig. 2(i) and the truth table in Table 2.

For each combination of Boolean input variable values, the

function f (a; b; c; d) is required to output a 0 (False), a 1

(True), or has no requirement. The lack of a requirement

is indicated with an X, or don’t-care symbol.

Expanding implicants as much as possible will ulti-

mately produce the prime implicants. To do this, combine

on-set and don’t-care elementary implicants using the re-

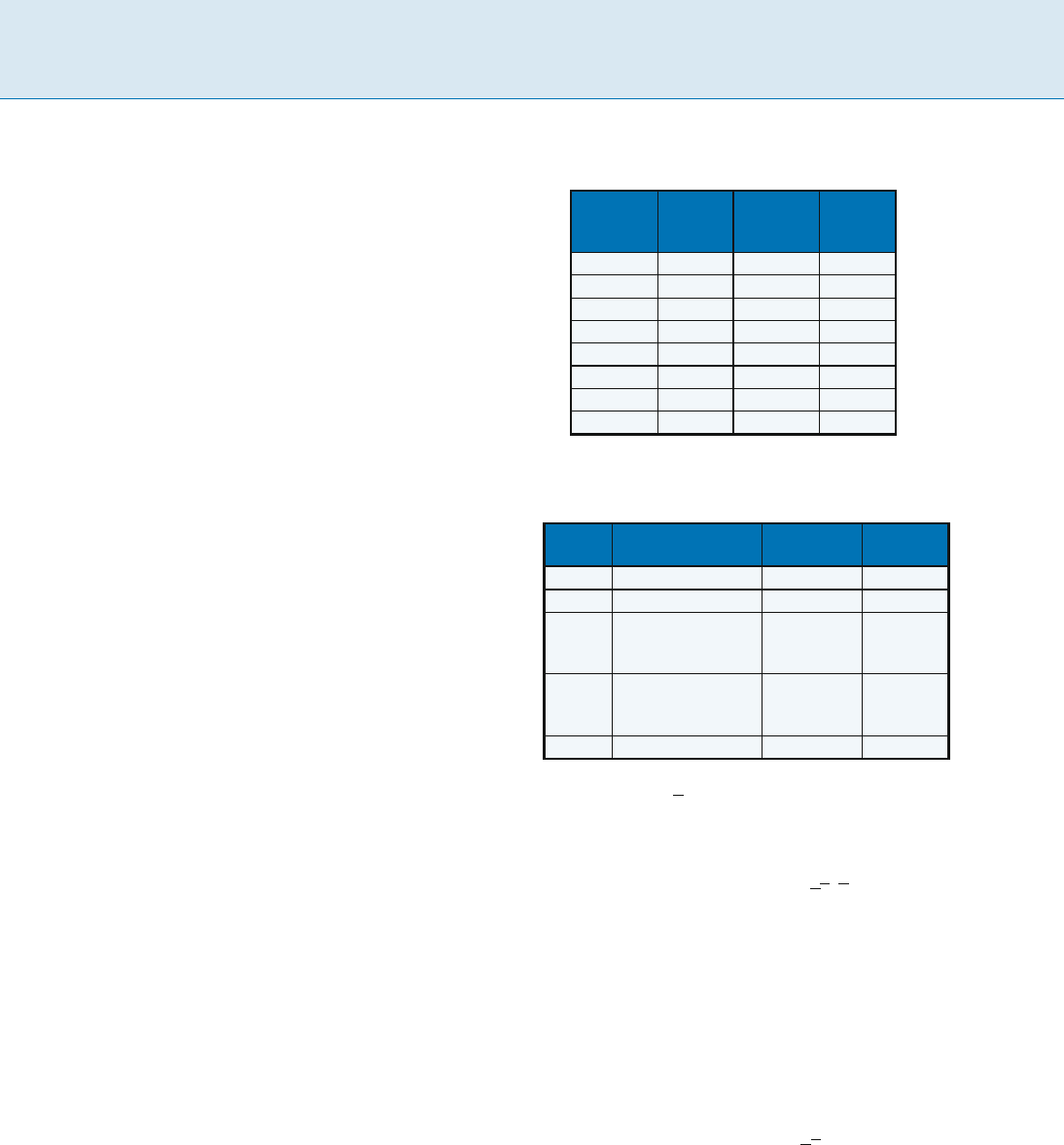
Two-Level Boolean Minimization, Table 2

Truth table of function f(a; b; c; d)

Elementary

implicant

(a; b; c; d)

Function

value

(a; b; c; d)

Elementary

implicant

Function

value

0000 X 1000 0

0001 0 1001 0

0010 1 1010 0

0011 1 1011 1

0100 0 1100 1

0101 0 1101 1

0110 0 1110 X

0111 0 1111 1

Two-Level Boolean Minimization, Table 3

Identifying prime implicants

Number

of ones

Elementary implicant

(a; b; c; d)

Second-order

implicant

Third-order

implicant

0 0000 X 00X0

1 0010 X 001X

0011 X

1100 X

X011

110X X

11X0 X

11XX

1011 X

1101 X

1110 X

1X11

11X1 X

111X X

4 1111 X

duction theorem (ab _ ab = b)showninTable1.Theel-

ementary implicants are circled in Fig. 2(ii) and listed in

the second column of Table 3.Inthistable,0sindicate

complemented variables and 1s indicate uncomplemented

variables, e. g., 0010 corresponds to

abcd. It is necessary

to determine all possible combinations of implicants. It is

impossible to combine non-adjacent implicants, i. e., those

that diﬀer in more than one variable. Therefore, it is not

necessary to consider combining any pair of implicants

with a number of uncomplemented variables diﬀering by

any value other than 1. This fact can be exploited by or-

ganizing the implicants based on the number of ones they

contain, as indicated by the ﬁrst column in Table 3.All

possible combinations of implicants in adjacent subsets

are considered. For example, consider combining 0010

with 0011, which results in 001X or

abc, and also consider

combining 0010 with 1100, which is impossible due to dif-

ferences in more than one variable. Whenever an impli-

cant is successfully merged, it is marked. These marked

implicants are clearly not prime implicants because the

implicants they produced cover them and contain fewer

literals. Note that marked implicants should still be used

for subsequent combinations. The merged implicants in

992 T Two-Level Boolean Minimization

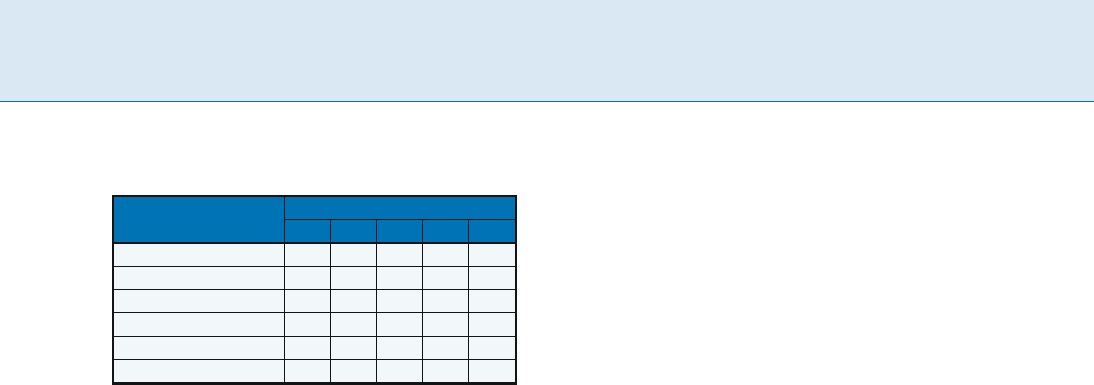
Two-Level Boolean Minimization, Table 4

Solving unate covering problem to select minimal cover

Requirements

(elementary implicants)

Resources (prime implicants)

00X0 001X X011 1X11 11XX

0010 X X

0011 X X

1011 X X

1100 X

1101 X

1111 X X

the third column of Table 3 correspond to those depicted

in Fig. 2(iii).

After all combinations of elementary implicants have

been considered, and successful combinations listed in the

third column, this process is repeated on the second-order

merged implicants in the third column, producing the

implicants in the fourth column. Implicants that contain

don’t-care marks in diﬀerent locations may not be com-

bined. This process is repeated until a column yielding no

combinations is arrived at. The unmarked implicants in

Table 3 aretheprimeimplicants,whichcorrespondtothe

implicants depicted in Fig. 2(iv).

After a function’s prime implicants have been identi-

ﬁed, it is necessary to select a minimal subset that cov-

ers the function. The problem can be formulated as unate

covering.AsshowninTable4, label each column of a ta-

blewithaprimeimplicant;theseareresourcesthatmay

be used to fulﬁll the requirements of the function. Label

each row with an elementary implicant from the on-set;

these rows correspond to requirements. Do not add rows

for don’t-cares. Don’t-cares impose no requirements, al-

though they were useful in simplifying prime implicants.

Mark each row–column intersection for which the ele-

mentary implicant corresponding to the row is covered by

the prime implicant corresponding to the column. If a col-

umn is selected, all the rows for which the column con-

tains marks are covered, i. e., those requirements are satis-

ﬁed. The goal is to cover all rows with a minimal-cost sub-

set of columns. McCluskey deﬁned minimal cost as having

a minimal number of prime implicants, with ties broken

by selecting the prime implicants containing the fewest

literals. The most appropriate cost function depends on

the implementation technology. One can also use a sim-

ilar formulation with other cost functions, e. g., minimize

the total number of literals by labeling each column with

a cost corresponding to the number of literals in the cor-

responding prime implicant.

One can use a number of heuristics to accelerate so-

lution of the unate covering problem, e. g., neglect rows

that have a superset of the marks of any other row, for

they will be implicitly covered and neglect columns that

have a subset of the marks of any other column if their

costs are as high, for the other column is at least as use-

ful. One can easily select columns as long as there exists

a row with only one mark because the marked column is

required for a valid solution. However, there exist prob-

lem instances in which each row contains multiple marks.

In the worst case, the best existing algorithms are required

to make tentative decisions, determine the consequences,

then backtrack and evaluate alternative decisions.

The unate covering problem appears in many applica-

tions. It is

NP-complete [5], even for the instances arising

during two-level minimization [9]. Its use in the Quine–

McCluskey method predates its categorization as an

NP-

complete problem by 16 years. A detailed treatment of this

problem would go well beyond the scope of this entry.

However, Gimpel [3]aswellasCoudertandMadre[2]

provide good starting points for further reading.

Some families of logic functions have optimal two-

level representations that grow in size exponentially in the

number of inputs, but have more compact multi-level im-

plementations. These families are frequently encountered

in arithmetic, e. g., a function indicating whether the num-

ber of on inputs is odd. Eﬃcient implementation of such

functions requires manual design or multilevel minimiza-

tion [1].

Applications

Digital computers are composed of precisely two things:

(1) implementations of Boolean logic functions and

(2) memory elements. The Quine–McCluskey method is

used to permit eﬃcient implementation of Boolean logic

functions in a wide range of digital logic devices, includ-

ing computers. The Quine–McCluskey method served as

a starting point or inspiration for most currently-used

logic minimization algorithms. Its direct use is contra-

dicted when functions are not amenable to eﬃcient two-

level implementation, e. g., many arithmetic functions.

Cross References

 Local Approximation of Covering and Packing

Problems

Recommended Reading

1. Brayton, R.K., Hachtel, G.D., Sangiovanni-Vincentelli, A.L.: Multi-

level logic synthesis. Proc. IEEE 78(2), 264–300 (1990)

2. Coudert, O., Madre, J.C.: New ideas for solving covering prob-

lems. In: Proc. Design Automation Conf., 1995, pp. 641–646

Two-Player Nash T 993

3. Gimpel, J.F.: A reduction technique for prime implicant tables.

IEEE Trans. Electron. Comput. 14(4), 535–541 (1965)

4. Karnaugh, M.: The map method for synthesis of combina-

tional logic circuits. Trans. AIEE, Commun. Electron. 72, 593–599

(1953)

5. Karp, R.M.: Reducibility among combinatorial problems. In:

Miller, R.E., Thatcher, J.W. (eds.) Complexity of Computer Com-

putations, pp. 85–103. Plenum Press, New York (1972)

6. McCluskey, E.J.: Minimization of Boolean functions. Bell Syst.

Tech. J. 35(6), 1417–1444 (1956)

7. Quine, W.V.: The problem of simplyfying truth functions. Am.

Math. Mon. 59(8), 521–531 (1952)

8. Quine, W.V.: A way to simplify truth functions. Am. Math. Mon.

62(9), 627–631 (1955)

9. Umans, C., Villa, T., Sangiovanni-Vincentelli, A.L.: Complexity of

two-level logic minimization. IEEE Trans. Comput.-Aided Des. In-

tegr. Circuits Syst. 25(7), 1230–1246 (2006)

Two-Person Game

 Complexity of Bimatrix Nash Equilibria

Two-Player Game

 Complexity of Bimatrix Nash Equilibria

Two-Player Nash

 Complexity of Bimatrix Nash Equilibria

Undirected Feedback Vertex Set U 995

Undirected Feedback Vertex Set

2005; Dehne, F ellows, Langston, Rosamond,

Stevens

2005; Guo, Gramm, Hüffner, Niedermeier,

Wernicke

JIONG GUO

Department of Mathematics and Computer Science,

University of Jena, Jena, Germany

Keywords and Synonyms

Odd cycle transversal

Problem Definition

The U

NDIRECTED FEEDBACK VERTEX SET (UFVS) prob-

lem is deﬁned as follows:

Input:AnundirectedgraphG =(V; E)andaninte-

ger k  0.

Task:Findafeedback vertex set F  V with jFjk

such that each cycle in G contains at least one vertex

from F. (The removal of all vertices in F from G re-

sults in a forest.)

Karp [11] showed that UFVS is NP-complete. Lund

and Yannakakis [12] proved that there exists some con-

stant >0 such that it is NP-hard to approximate the op-

timization version of UFVS to within a factor of 1 + .

The best-known polynomial-time approximation algo-

rithm for UFVS has a factor of 2 [1,4]. There is a simple

and elegant randomized algorithm due to Becker et al. [3]

which solves UFVS in O(c4

kn)timeonann-vertex and

m-edge graph by ﬁnding a feedback vertexsetof size k with

probability at least 1  (1 4

k

)

for an arbitrary con-

stant c. An exact algorithm for UFVS with a running time

Supported by the Deutsche Forschungsgemeinschaft, Emmy

Noether research group PIAF (ﬁxed-parameter algorithms), NI 369/4

of O(1.7548

) was recently found by Fomin et al. [9]. In

the context of parameterized complexity [8,13], Bodlaen-

der [5] and Downey and Fellows [7] were the ﬁrst to show

that the problem is ﬁxed-parameter tractable, i. e., that the

combinatorial explosion when solving it can be conﬁned

to the parameter k. The currently best ﬁxed-parameter al-

gorithm for UFVS runs in O(c

mn) for a constant c [6,10]

(see [6] for the so far best running time analysis leading to

aconstantc =10:567). This algorithm is the subject of this

entry.

Key Results

The O(c

mn)-time algorithm for the UNDIRECTED FEED-

BACK VERTEX SET is based on the so-called “iterative

compression” technique, which was introduced by Reed et

al. [14]. The central observation of this technique is quite

simple but fruitful: To derive a ﬁxed-parameter algorithm

for a minimization problem, it suﬃces to give a ﬁxed-

parameter “compression routine” that, given a size-(k +1)

solution, either proves that there is no size-k solution or

constructs one. Starting with a trivial instance and iter-

atively applying this compression routine a linear num-

ber of rounds to larger instances, one obtains a ﬁxed-

parameter algorithm of the problem. The main challenge

of applying this technique to UFVS lies in showing that

there is a ﬁxed-parameter compression routine.

The compression routine from [6,10] works as follows:

1 Consider all possible partitions (X, Y)ofthesize-

(k + 1) feedback vertex set F with jXjk under the

assumption that set X is entirely contained in the new

size-k feedback vertex set F

and Y \ F

= ;

2 For each partition (X, Y), if the vertices in Y induce cy-

cles, then answer “no” for this partition; otherwise, re-

move the vertices in X. Moreover, apply the following

data reduction rules to the remaining graph:

 Remove degree-1 vertices.

 If there is a degree-2 vertex v with two neighbors v

and v

,wherev

… Y or v

… Y,thenremovev and

connect v

and v

. If this creates two parallel edges

996 U Unified Energy-Efficient Unicast and Broadcast Topology Control

between v

and v

, then remove the vertex of v

and v

that is not in Y and add it to any feedback

vertex set for the reduced instance.

Finally, exhaustively examine every vertex set S with

size at most k jXj of the reduced graph as to

whether S can be added to X to form a feedback ver-

tex set of the input graph. If there is one such vertex set,

then output it together with X as the new size-k feed-

back vertex set.

The correctness of the compression routine follows from

its brute-force nature and the easy to prove correctness of

the two data reduction rules. The more involved part is to

show that the compression routine runs in O(c

m)time:

There are 2

+1 partitions of F into the above sets (X, Y)

and one can show that, for each partition, the reduced

graph after performing the data reduction rules has at

most dk vertices for a constant d;otherwise,thereisno

size-k feedback vertex set for this partition. This then gives

the O(c

m)-running time. For more details on the proof

of the dk-size bound see [6,10].

Given as input a graph G with vertex set fv

;:::;v

the ﬁxed-parameter algorithm from [6,10] solves UFVS

by iteratively considering the subgraphs G

:= G[fv

;:::;

g]. For i = 1, the optimal feedback vertex set is empty.

For i > 1, assume that an optimal feedback vertex set X

for G

is known. Obviously, X

[fv

i+1

g is a solution set

for G

i+1

. Using the compression routine, the algorithm

can in O(c

m) time either determine that X

[fv

i+1

g is

an optimal feedback vertex set for G

i+1

,or,ifnot,com-

pute an optimal feedback vertex set for G

i+1

.Fori = n,we

thus have computed an optimal feedback vertex set for G

in O(c

mn)time.

Theorem 1 U

NDIRECTED FEEDBACK VERTEX SET can

be solved in O(c

mn) time for a constant c.

Applications

The U

NDIRECTED FEEDBACK VERTEX SET is of funda-

mental importance in combinatorial optimization. One

typical application, for example, appears in the context of

combinatorial circuit design [1]. For applications in the ar-

eas of constraint satisfaction problems and Bayesian infer-

ence, see Bar-Yehuda et al. [2].

Open Problems

It is open to explore the practical performance of the de-

scribed algorithm. Another research direction is to im-

prove the running time bound given in Theorem 1. Fi-

nally, it remains a long-standing open problem whether

the F

EEDBACK VERTEX SET on directed graphs is ﬁxed-

parameter tractable. The answer to this question would

represent a signiﬁcant breakthrough in the ﬁeld.

Recommended Reading

1. Bafna, V., Berman, P., Fujito, T.: A 2-approximation algorithm

for the undirected feedback vertex set problem. SIAM J. Dis-

cret. Math. 3(2), 289–297 (1999)

2. Bar-Yehuda, R., Geiger, D., Naor, J., Roth, R.M.: Approximation

algorithms for the feedback vertex set problem with applica-

tions to constraint satisfaction and Bayesian inference. SIAM

J. Comput. 27(4), 942–959 (1998)

3. Becker, A., Bar-Yehuda, R., Geiger, D.: Randomized algorithms

for the Loop Cutset problem. J. Artif. Intell. Res. 12, 219–234

(2000)

4. Becker, A., Geiger, D.: Approximation algorithms for the Loop

Cutset problem. In: Proc. 10th Conference on Uncertainty in Ar-

tificial Intelligence, pp. 60–68. Morgan Kaufman, San Fransisco

(1994)

5. Bodlaender, H.L.: On disjoint cycles. Int. J. Found. Comp. Sci.

5(1), 59–68 (1994)

6. Dehne, F., Fellows, M.R., Langston, M.A., Rosamond, F.,

Stevens, K.: An O(2

O(k)

) FPT algorithm for the undirected

feedback vertex set problem. In: Proc. 11th COCOON. LNCS,

vol. 3595, pp. 859–869. Springer, Berlin (2005). Long version to

appear in: J. Discret. Algorithms

7. Downey, R.G., Fellows, M.R.: Fixed-parameter tractability and

completeness. Congres. Numerant. 87, 161–187 (1992)

8. Downey, R.G., Fellows, M.R.: Parameterized Complexity.

Springer, Heidelberg (1999)

9. Fomin, F.V., Gaspers, S., Pyatkin, A.V.: Finding a minimum feed-

back vertex set in time O(1.7548

). In: Proc. 2th IWPEC. LNCS,

vol. 4196, pp. 184–191. Springer, Berlin (2006)

10. Guo, J., Gramm, J., Hüffner, F., Niedermeier, R., Wernicke, S.:

Compression-based fixed-parameter algorithms for Feedback

Vertex Set and Edge Bipartization. J. Comp. Syst. Sci. 72(8),

1386–1396 (2006)

11. Karp, R.: Reducibility among combinatorial problems. In:

Miller, R., Thatcher, J. (eds.) Complexity of Computer Compu-

tations, pp. 85–103. Plenum Press, New York (1972)

12. Lund, C., Yannakakis, M.: The approximation of maximum sub-

graph problems. In: Proc. 20th ICALP. LNCS, vol. 700, pp. 40–51.

Springer, Berlin (1993)

13. Niedermeier, R.: Invitation to Fixed-Parameter Algorithms. Ox-

ford University Press, Oxford (2006)

14. Reed, B., Smith, K., Vetta, A.: Finding odd cycle transversals.

Oper. Res. Lett. 32(4), 299–301 (2004)

Unified Energy-Efficient Unicast

and Broadcast Topology Control

 Degree-Bounded Planar Spanner with Low Weight

University Admissions P roblem

 Hospitals/Residents Problem

Utilitarian Mechanism Design for Single-Minded Agents U 997

Using Visualization in the Empirical

Assessment of Algorithms

 Visualization Techniques for Algorithm Engineering

Utilitarian Mechanism Design

for Single-Minded Agents

2005; Briest, Krysta, Vöcking

PIOTR KRYSTA

,BERTHOLD VÖCKING

Department of Computer Science, University of

Liverpool, Liverpool, UK

Department of Computer Science, RWTH Aachen

University, Aachen, Germany

Keywords and Synonyms

Forward (combinatorial, multi-unit) auction

Problem Definition

This problem deals with the design of eﬃciently com-

putable incentive compatible, or truthful, mechanisms for

combinatorial optimization problems with selﬁsh one-

parameter agents and a single seller. The focus is on ap-

proximation algorithms for NP-hard mechanism design

problems. These algorithms need to satisfy certain mono-

tonicity properties to ensure truthfulness.

A one parameter agent is an agent who as her private

data has some resource as well as a valuation,i.e.,themax-

imum amount of money she is willing to pay for this re-

source. Sometimes, however, the resource is assumed to

be known to the mechanism. The scenario where a sin-

gle seller oﬀers these resources to the agents is primarily

considered. Typically, the seller aims at maximizing the

social welfare or her revenue. The work by Briest, Krysta

and Vöcking [6] will mostly be considered, but also other

existing models and results will be surveyed.

Utilitarian Mechanism Design

A famous example of mechanism design problems is given

by combinatorial auctions (CAs), in which a single seller,

auctioneer, wants to sell a collection of goods to poten-

tial buyers. A wider class of problems is encompassed

by a utilitarian mechanism design (maximization) prob-

lem ˘ deﬁned by a ﬁnite set of objects

A, a set of feasi-

ble outputs O

 A

and a set of n agents. Each agent

declares a set of objects S

 A and a valuation func-

tion v

: P(A)  A

! R by which she values all possible

outputs. Given a vector S =(S

;:::;S

)ofdeclarations

one is interested in output o



2 O

maximizing the social

welfare,i.e.,o



2 argmax

o2O

i=1

; o). In CAs, an

object a corresponds to a subset of goods. Each agent de-

clares all the subsets she is interested in and the prices she

would be willing to pay. An output speciﬁes the sets to be

allocated to the agents.

Here, a limited type of agents called single-minded

is considered, introduced by Lehmann et al. [10]. Let



 A

be a reﬂexive and transitive relation on A,

such that there exists a special object ¿ 2

A with ¿  a

for any a 2

A to model the situation in which some

agent does not contribute to the solution at all. For

a; b 2

A (a; b) 2 R



will be denoted by a  b.The

single-minded agent i declares a single object a

and is fully

deﬁned by her type (a

; v

), with a

2 A and v

> 0. The

valuation function introduced earlier reduces to

; o)=

(

; if a

 o

0 ; else :

Agent i is called known if object a

is known to the

mechanism [11]. Here, mostly unknown agents will be

considered. Intuitively, each a

corresponds to an ob-

ject agent i oﬀers to contribute to the solution, v

de-

scribes her valuation of any output o that indeed selects

.InCAs,relationR



is set inclusion: an agent inter-

ested in set S will is also satisﬁed by S

with S  S

For ease of notation let (a; v)=((a

; v

);:::;(a

; v

)),

i

; v

i

)=((a

; v

);:::;(a

i1

; v

i1

); (a

i+1

; v

i+1

);:::;

; v

)) and ((a

; v

); (a

i

; v

i

)) = (a; v).

Mechanism

A mechanism M =(A; p) consists of an algorithm A

computing a solution A(a; v) 2 O

and an n-tuple

p(a; v)=(p

(a; v);:::;p

(a; v)) 2 R

of payments col-

lected from the agents. If a

 A(a; v)

,agenti is se-

lected,andletS(A(a; v)) = fija

 A(a; v)

g be the set

of selected agents. Agent i’s type is her private knowl-

edge. Thus, the types declared by agents may not

match their true types. To reﬂect this, let (a



; v



)re-

fer to agent i’s true type and (a

; v

)bethedeclared

type. Given an output o 2 O

,theutility of agent i is

(a; v)=v



; o)  p

(a; v). Each agent’s goal is to max-

imize her utility. To achieve this, she will try to ma-

nipulate the mechanism by declaring a false type if this

could result in higher utility. A mechanism is called truth-

ful,orincentive compatible,ifnoagenti can gain by

lying about her type, i. e., given declarations (a

i

; v

i

((a



; v



); (a

i

; v

i

))  u

((a

; v

); (a

i

; v

i

)) for any

; v

) 6=(a



; v

