Калинин Н.А., Толмачёва Н.И. Космические методы исследований в метеорологии
Подождите немного. Документ загружается.

Глава 7
ПРОГНОЗИРОВАНИЕ НА ОСНОВЕ ЦИФРОВОЙ
ОБРАБОТКИ ИЗОБРАЖЕНИЙ
Одной из важных как в научном, так и в прикладном плане за-
дач современной метеорологии является разработка объективных ав-
томатизированных методов исследования закономерностей протекания
мезомасштабных метеорологических процессов и связанных с ними
опасных метеорологических явлений. Для ее решения в последние го-
ды стала быстро развиваться технология сверхкраткосрочного (соглас-
но терминологии ВМО, с заблаговременностью до 12 ч) и текущего
(постоянно обновляемые по мере поступления метеорологической ин-
формации с заблаговременностью до 3 ч, по терминологии ВМО —
наукастинг (Nowcasting) прогнозирования мезомасштабных метеоро-
логических процессов.
Несмотря на наличие различных подходов, задача специализи-
рованной цифровой обработки космических изображений до настоя-
щего времени полностью не решена, особенно при совместном усвое-
нии такой разнородной метеорологической информации, как спутни-
ковая и станционная.
В данной теме изложены общие принципы обработки изобра-
жений с использованием со
временных ПК, а также вопросы построе-
ния центральной линии объекта, сегментации и выделения контура
объекта. Приводятся результаты использования рассмотренных мето-
дов для решения конкретных метеорологических задач. Указанные
методы призваны помочь метеорологу в оперативной обработке спут-
никовых изображений для анализа и составления прогноза погоды раз-
личной заблаговременности.
7.1. ОБЩИЕ ПРИНЦИПЫ И МЕТОДЫ ЦИФРОВОЙ
ОБРАБОТКИ СПУТНИКОВЫХ ИЗОБРАЖЕНИЙ
Методы цифровой обработки изображения применяются тогда,
когда необходимо:
– повысить качество изображения или его модифицировать для
того, чтобы выделить некоторые аспекты информации, содержащиеся
в изображении;
– классифицировать, сравнить или измерить элементы в изоб-
ражении;
– скомбинировать части изображений или реорганизовать эле-
менты изображения.
282
В настоящее время имеется обширная литература по цифровой
обработке изображений. Большинство решаемых современной метео-
рологи
его используются черно-белые полутоновые изо-
бражени
интенс
иной
Δλ
. Очевидно, что подобные изображения
можно описа
вности излучения в зависимости от параметров х и у, однозначно
определяющи каждой точки. При рассмотре
кационных и ункция В(х,у) будет описыват
венное
предпочтитель ажения, п
ставленные в цифровом виде, т. е. в виде матрицы. Каждая такая мат-
твует прямоугольник, определяемый не-
равенс
изображение мало
отлича
допустить достаточно большое количество уровней квантова-
ния. Частным случаем квантования является двоичное изображение, в
ей задач по анализу видеоданных отличается от традиционных
задач обработки изображений. Эти отличия приводят к необходимости
разработки методов и алгоритмов анализа применительно к метеоро-
логической информации, при этом традиционные методы цифровой
обработки используются как вспомогательные.
Под изображением будем понимать зафиксированное на каком-
либо носителе отображение пространственного распределения собст-
венного или отраженного излучения некоторого сюжета. В дистанци-
онных методах зондирования системы «подстилающая поверхность–
атмосфера» чаще вс
я, отображающие пространственное распределение излучения,
ивность которого регистрируется внутри некоторого спектраль-
ного интервала шир
ть одной функцией В(х, у), отображающей изменения ин-
тенси
х положение нии радиоло-
зображений ф ь пространст-
распределение отражаемости. Значение функции В(х,у), описы-
вающей изображение в некоторой точке, будем называть яркостью
изображения в этой точке.
При интерпретации метеорологической видеоинформации
но использовать дискретизованные изобр ред-
рица с действительными, неотрицательными элементами является
цифровым представлением изображения. Пусть для каждой пары (i, j),
где 1 < i < M, 1 < j < N, сущес
твами i – 1 < x < i , j – 1 < у < j. Тогда можно считать, что каж-
дой матрице B размерности M×N
соответствует изображение, значения
яркости которого в квадрате b
ij
равны постоянной величине a
ij
для
каждой пары (i, j). Построенное таким образом изображение называет-
ся дискретным. Естественно, что каждое исходное
ется от дискретного изображения размерности M×N лишь при
достаточно больших значениях N и M.
При цифровой обработке изображений считается, что функция
В(х,у) может принимать только конечное количество значений, т. е.
сигнал, соответствующий изображению, квантуется. Можно показать,
что исходное изображение практически не отличается от квантованно-
го, если
283
которо
точками Ви и Bk опреде-
ляется
ого пространства расстояние на-
ходится по формуле
R
N
(Bu, Bk) = [(Ви
1
– Bk
1
)
2
+...+ (Bu
N
или
м функция В(х,у) может принимать только два значения: нуль и
единицу.
Известно, что квантованное изображение отличается от исход-
ного. Это означает, что оба изображения будут представлены различ-
ными точками. Искажение при квантовании (при условии, что сами
системы квантования не вносят дополнительных искажений) характе-
ризуется расстояниями между этими точками.
Рассмотрим случай в трехмерном пространстве. Пусть точка Ви
с координатами Ви
x
Bu
y
и Ви
z
является точкой реального изображения,
a Bk — соответственно точка квантованного изображения с координа-
тами Bk
x
, Bk
y
и Bk
z
. Тогда расстояние между
выражением
R(Bu,Bk) = [(Ви
x
– Bk
x
)
2
+ (Bu
y
– Bk
y
)
2
+ (Bu
z
– Bk
z
)
2
]
1/2
. (5.1)
В самом общем случае N–мерн
–Bk
N
)
2
]
1/2
(5.2)
R
R
N
(Bu, Bk) =
2/1
11
22
2)(
⎥
⎦
⎤
⎢
⎣
⎡
−+
∑∑
==
N
i
ii
N
i
ii
BkBuBkBu
. (5.3)
Видно, что функция R
R вели-
чина.
(Bu, Bk) — всегда неотрицательная
N
Только при Ви
i
= Вk
i
т.е. при точном совпадении обоих изобра-
жений, R
R
N
(Bu
i
, Bk
i
)=0. Во всех остальных R
N
R
на исходным и кванто-
ванны
и, тем меньше значение R
N
(Bu
i
, Bk
i
).
При интерпретации спутниковых ажений, и особенно при
нейтрального
(Bu
i
, Bk
i
)>0. Первая сум-
ма
∑
=
+
N
i
ii
BkBu
1
22
)(
соответствует мощности. Вторая сумма
∑
=
N
i
Bu
1
2
ii
Bk
пропорцио льна корреляции между
м изображениями. Чем больше корреляция между обоими изо-
бражениям
изобр
визуально-инструментальной интерпретации с помощью
градационного клина, всегда можно найти или выбрать такое значе-
ние Δ, чтобы при R
R
параметром для всех оцедур цифровой обработки,
приведенных далее, будет служить утоновое дискретизованное
изобра
N
(Bu
i
, Bk
i
) ≤ Δ квантованное изображение относи-
лось к заранее выбранному или заданному эталону.
Входным пр
пол
жение, представленное в виде цифрового массива яркостей B(i,
j), i =1, М, j =1, N, где М и N — размеры изображения, заданного на
прямоугольной сетке с конечным разрешением. Каждый элемент
массива может принимать значение от 0 (черный цвет) до 15 (белый
цвет).
284

В задачах обработки изображений оследние нередко интерпре-
тируются как случайные процессы двух еменных, т.е. как случай-
ные п
сива м
как ме
размером N×M элементов, формула вычисления начальных
моментов т
k
k–го поряд
п
пер
оля. Тогда непосредственно по имеющейся реализации изобра-
жения или с помощью предварительно полученной гистограммы мож-
но оценить различные статистические моменты, характеризующие
обрабатываемое изображение. Кроме того, для обрабатываемого мас-
огут быть оценены значения экстремальных статистик (напри-
мер, минимум или максимум), размах и энтропия. Энтропия может
быть использована либо как инструментарий для введения различных
мер количества информации, присутствующего в изображениях, либо
ра хаотичности данного изображения.
Применительно к анализу изображения, представленному как
матрица В
ка имеет вид
∑∑
=
M
k
N
jiBm ).,(
1
(5.4)
==
⋅
ji
MN
11
Начальный момент первого порядка т
k
начале вычисляются начальные моменты, а за-
тем использую мо-
ментов в центр
2
1
является мате-
матическим ожиданием; начальный момент второго порядка т
2
—
средним квадратом; моменты третьего и четвертого порядков исполь-
зуются для вычисления коэффициентов асимметрии и эксцесса.
Чтобы не перебирать дважды элементы поля при расчете цен-
тральных моментов, в
тся известные выражения для пересчета начальных
альные:
u
2
= т
2
– m
1
;
u
3
= m
3
– 3m
1
m
2
+ 2 m
1
2
;
u
4
= m
4
– 4m
1
m
3
+ 6 m
1
2
m
2
– m
1
4
.
Центральный момент второго порядка и
2
является дисперсией, а
величина
2
u=
σ
представляет собой среднеквадратическое отклонение.
С центральным моментом третьего порядка u
3
связан коэффи-
циент асимметрии q
1
, характеризующий скошенность распределения
вероятностей:
.
3
3
1
σ
u
ующий крутость распределения:
q =
Для симметричного (относительно математического ожидания)
распределения коэффициент асимметрии равен нулю.
С центральным моментом четвертого порядка и
4
связан коэф-
фициент эксцесса q
2
, характериз
285

3
4
4
2
−
=
σ
u
q
.
Коэффициент эксцесса нормального распределения равен нулю.
Если кривая плотности вероятности имеет более острую и высокую
вершину по сравнению с нормальным распределением, то эксцесс по-
ложителен, если более низкую и пологую — эксцесс отрицателен.
Энтропия чаще всего применяется в случаях асимметричных
или многовершинных распределений, когда использование таких чи-
словых характеристик, как среднее значение, среднеквадратическое
отклонение и моменты высших порядков, теряет наглядность.
При равномерном законе распределения (полная хаотичность)
энтропия достигает максимума, который зависит только от количества
уровней:
I = log (h – h
2 max min
min
+ 1),
где h
знаки могут
быть р
изображениях гео-
метри ых объектов, обу-
словле
икой.
— значения максимального и минимального уровня соответст-
венно.
Приведенные характеристики позволяют количественно оце-
нить результат применения того или иного метода цифровой обработ-
ки изображений. Однако они являются слишком общими для того,
чтобы опираться на них при решении задач выделения и идентифика-
ции облачности. Более привлекательными в этом отношении являются
текстурные признаки.
7.1.1. Текстурный анализ изображений
Образ объекта и его состояние складываются из определенных
дешифровочных признаков, по которым этот объект распознается.
Применительно к космическим изображениям, поступающим с метео-
рологических спутников, основные дешифровочные при
азбиты на следующие группы:
– оптические дешифровочные признаки, под которыми пони-
маются отображаемые на космических снимках тональные особенно-
сти природных и антропогенных объектов, процессов и явлений, про-
являющиеся благодаря специфике воздействия на них и последующего
преобразования атмосферой прямой и рассеянной солнечной радиа-
ции;
– структурно-текстурные дешифровочные признаки, под кото-
рыми понимаются отображаемые на космических
ческие особенности природных и антропогенн
нные их взаимным пространственно-временным расположением
и взаимосвязанной динам
286
Промежуточное положение между тональными и структурно-
текстурными особенностями природных образований, отображаемыми
на кос
геометрических свой-
ствах.
о к тоновым изменениям внешнего вида местности. Следова-
тельно
новном на тональные
призна на их все более
мелки
ав реальной атмосферы, высота полета спутни-
ка, спо
ричине объекты с одними и теми же спек-
тральн
представленных на спутниковых снимках текстур может
быть и
е
мических фотоизображениях, занимают дешифровочные при-
знаки, обусловленные различиями разрешающих способностей изо-
бражений. С увеличением разрешающей способности снимков инфор-
мативность интегральных характеристик объектов, проявляющихся в
их оптических свойствах, уступает в информативности индивидуаль-
ным характеристикам, проявляющимся в их
Так, чем более обобщено изображение, тем менее оно чувстви-
тельн
, стремление получать изображение все более высокого разре-
шения равносильно переходу от «опоры» в ос
ки при интерпретации изображений к «опоре»
е структурно-текстурные признаки.
Дешифрирование космических снимков с низкой разрешающей
способностью основывается главным образом на данных о плотности
фототона, определяемой общим или спектральными альбедо изучае-
мых объектов. Недостатком этих спектральных характеристик (альбе-
до) является их существенная зависимость от условий съемки (сезон
года, время суток, сост
соб формирования изображения, высота и азимут Солнца), что
вносит большую долю неопределенности в результаты интерпретации
изображений. По этой п
ыми характеристиками могут выглядеть по-разному на различ-
ных изображениях одной и той же территории. Опознать все многооб-
разие параметров состояния природных образований по тональным
различиям принципиально невозможно. Чисто белым тоном, напри-
мер, могут отображаться на снимках облака, снег, лед, пески, блики на
водной поверхности и другие крупные и мелкие объекты.
Привлечение в качестве критерия дешифрирования еще и ри-
сунка текстуры изображения резко повышает вероятность распознава-
ния. Это обусловлено тем, что текстурные дешифровочные признаки
имеют важное преимущество перед тональными признаками, которое
заключается в их меньшей подверженности влияниям условий съемки,
благодаря чему они в первую очередь используются дешифровщиком
в качестве демаскирующих признаков.
Анализ
спользован для решения следующих задач:
– классификация или распознавание текстур;
– обнаружение объектов на изображ ниях с использованием
информации о текстуре;
287
– разделение изображений на фрагменты путем использования
различий в текстуре.
Главной проблемой анализа текстурной информации является
формирование системы признаков, позволяющих оперативно осущест-
влять классификацию и распознавание исследуемых изображений. Под
признаками текстур обычно понимают характерные свойства, общие
для всех текстур дан имозависимые при-
ванные на измерении пространственных час-
тиках
– признаки описаний тов.
Большое ра получил струк-
рных и чисто
статистических под-
ход к описанию текстур.
В силу необходимости максимального ускорения обработки ви-
зуальн релированности текстурных признаков
возникает проблема выбора из множества п оженных признаков
наиболее информативных. Были проведены исследования качеств 28
призна х: выбор признаков, обладающих минималь-
ным размером области существования и имеющ максимальное рас-
стояние между этими областями. Анализ полученных данных позво-
лил установить текстурных признаков, обладаю-
щих в чествами, наиболее пригодным
является метод, основанный на сравнении а орных вероятно-
стей. При использовании этого метода в качестве меры разброса при-
знаков
но-
го признака.
Проведенные исследования показали, чт наиболее компактны-
ми кластерами обладают пять признаков. Для их количественного опи-
ного появления
ежности P
δϕ
(i, j).
ного класса. Условно эти вза
знаки можно объединить в следующие группы:
– признаки, осно
тот;
– признаки, основанные на статистических характерис
уровней интенсивности эле ; ментов разложения
структурных элемен
звитие в работах по анализу текстур
турный подход к их описанию, основанный на анализе формы и раз-
меров элементов, составляющих текстуру, вычислении локальных
признаков и анализе распределения элементов текстуры по полю изо-
бражения. Это обусловлено тем, что статистические методы по мере
уменьшения количества однородных элементов текстуры становятся
менее эффективными.
Наметилась тенденция к синтезу чисто структу
подходов в единый структурно статистический-
ой информации и кор
редл
ков в двух аспекта
их
, что для выделения
ысокими разделительными ка
постери
принимается их дисперсия: минимуму дисперсии соответствует
минимальный размер области существования (кластера) того или и
о
сания используется матрица вероятности совмест
уровней яркости пар смежных точек или матрица см
288

Каждый элемент ма
ты, с которой кажда
, отстоящих друг от друга на расстояние
δ
в направлении
ϕ
,
на изображении. В данной работе для оценки матрицы
смежности вычисля
правлениям при межпиксельном расстоянии
δ
=1:
P
ij
= (P
0
+ P
45
+ P
90
+ P
35
) / 4 ,
где индексы в правой части соот тствуют четыре направлениям
ϕ
,
заданным в градусах.
трицы смежности соответствует значению часто-
я пара точек (одна с яркостью i и другая с яр-
костью j)
встречается
лась средняя матрица смежности по четырем на-
ве м
Обозначив через N
x
и N
y
размер изображения по осям Х и Y со-
ответственно, определим нормализованную матрицу смежности
p(i, j) = P
ij
/ N
Σ
,
где
N
Σ
= N
y
(N
x
+ 1) + N
x
(N
y
+ 1) +2N
x
N
y
представляет собой количество пар, примыкающих друг к другу по
горизонтали и диагонали элементов разрешения, а произведение N
x
N
y
определяет общее число элементов разрешения в оцифрованном изо-
бражении. Тогда для пяти упомянутых ранее признаков можно привес-
ти следующие соотношения, позволяющие осуществить их количест-
венную оценку:
– момент обратной разности (обратный момент)
∑∑
==
−+
=
N
j
N
i
jip
j
)
i
f
1
2
1
1
),(
(1
1
;
опия
;
– суммарная энтр
[]
∑
++
=
N
ipipf
2
2
)(log)(
;
=
i 2
– энтропия
NN
[]
∑∑
==
−=
ji
jipjipf
11
3
),(log),(
– дифференциальная энтропия
[]
∑
−
=
−−
−=
1
0
4
)(log)(
N
i
ipipf
;
– максимальный коэффициент корреляции f
14
, равный корню
квадратному из второго наибольшего собственного значения Q(i,j)
∑
=
=
N
k
yx
kpip
kjpkip
jiQ
1
)()(
),(),(
),(
.
Здесь N — количество уровней квантования яркости;
289
∑∑
NN
==
+
=
ji
jipkp
11
),()(
— гистограмма сумм значений яркости (k = 2, 3,
…, 2N);
— гистограмма разностей значений яркости (k =
0, 1, ..., N–1);
Матрицы смежности могут быть представлены в виде поля
16×16 элементов. Каждый элемент с координатами i и j определяется
путем подсчета того, сколько раз пара яркостей (i, j) в х направ-
ается на изображении. Каждый элемен матрицы обо-
оттенком из черно-белой шкалы яркостей. Черному
цвету соответствует максимальное значение Р
ij
, белому — минималь-
ное. Для каждого изображения с помощью его матрицы смежности
могут быть вычислены энтропия и обратный момент.
В качестве количественной характеристики изображений кроме
уже указанных текстурных признаков в данной работе были проанали-
зированы также показатели контраста и однородности, которые рас-
считывались по следующим формулам:
– контраст
– однородность
результатов цифровой обработки серии спутниковых
изображений по этим текстурным признакам позволил сделать опре-
деленные выводы.
Большое значение обратного момента показывает высокую кон-
центрацию событий на главной диагонали матрицы смежности (при i =
j) и представляет крупнозернистую или грубую текстуру (рис. 7.1, а).
Если изображение имеет мелкозернистую текстуру, то значения эле-
ментов матрицы смежности распределены в пределах матрицы отно-
сительно равномерно и изображение описывается меньшими значе-
ниями обратного момента (рис. 7.1, б).
Наименьшая однородность наблюдается при равновероятных
уровнях яркости, т.е. при размытой матрице смежности. И наоборот,
когда элементы матрицы смежности концентрируются а главной диа-
гонали, однородность имеет наиб льшее значение. онтраст имеет
меньшие числовые туре, чем при тонкой
∑∑
==
−
=
N
j
N
i
jipkp
11
),()(
∑
=
=
N
j
x
jipip
1
),()(
,
∑
=
=
N
i
y
jipjp
1
),()(
.
четыре
т лениях встреч
значается своим
∑∑
==
−=
N
j
ij
N
i
pjiC
1
2
1
)(
;
∑∑
==
=
N
j
ij
N
i
pU
1
2
1
.
Анализ
н
Ко
значения при грубой текс
290
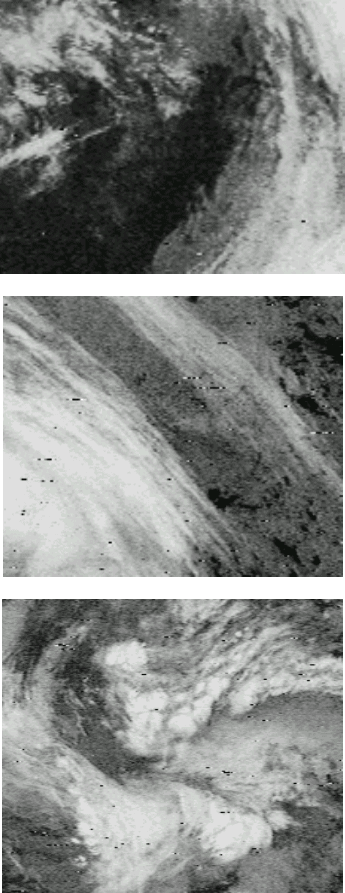
а)
б)
в)
Рис. 7 1. Примеры текстуры .
291
