Кадеев А.А. Домашняя работа по алгебре за 11 класс
Подождите немного. Документ загружается.

120
()
=+=−=−=−=
π
πππ
∫∫∫
2
0
2
0
2
0
2
0
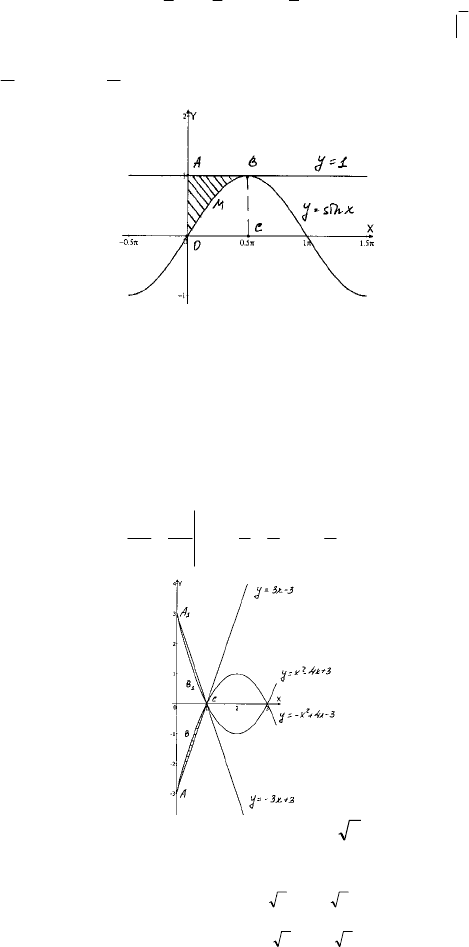
cossin1sin1 xxdxxxdxdxSSS
OBCOABCABO
1
2
100
2
−
π
=−−+
π
=
№ 1022
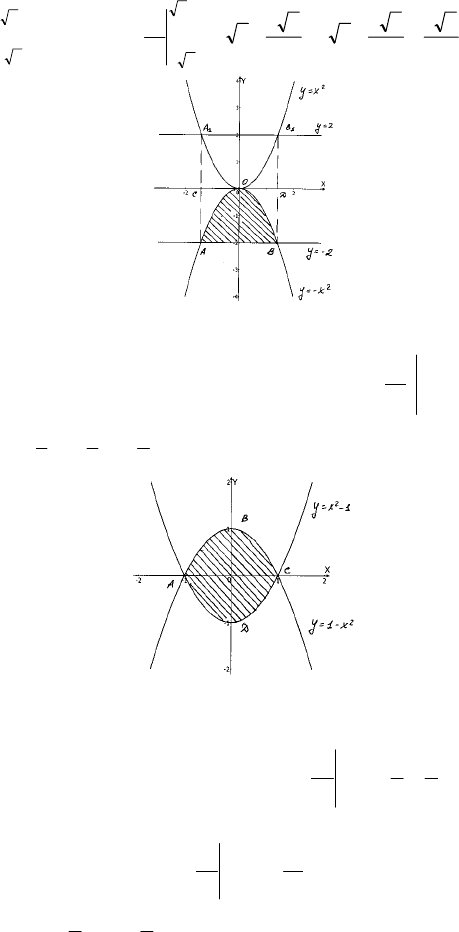
1) Найдем прямую у = kx + b
(0; –3); –3 = k ⋅ 0 + b, b = –3; (1; 0); 0 = k – 3, k =–3, y = 3x – 3
–х
2
+ 4х – 3 = 3х – 3, х
2
– х = 0, х
1
= 0, х
2
= 1
ABС – искомая фигура
Рассмотрим симметричную ей фигуру A
1
B
1
С
1
.
()
(
)
=+−−+−=−==
∫∫
1
0
2
1
0
3433
111111
dxxxdxxSSSS
CBOACOAABCCBA
()
6
1
0
2
1
3
1
23
1
0
23
1
0
2
=++−=+−=+−=
∫
xx
dxxx
2) у = –х
2
, у = –2, –х
2
= –2, х
2
= 2, х = 2±
AОB – искомая фигура
Рассмотрим симметричную ей фигуру A
1
ОB
1
.
=−=−==
∫∫
−−
2
2
2
2
2
2
11111
dxxdxSSSS
DOBCABDOAOBAAOB
121
()
3
28
3
22
22
3
22
22
3
22
2
2
3
2
2
2
=−+−=−=−=
−
−
∫
x
xdxx .
3) у = 1 – х
2
; у = х
2
– 1, 1 – х
2
= х
2
– 1, 2х
2
= 2, х = ± 1
ABСD – искомая фигура, S
ABC
= S
ADC
()
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=−==+=
−
−
∫
1
1
3
1
1
2
3
2122
x
xdxxSSSS
ABCADCABCABCD
3
2
2
3
1
1
3
1
12 =
⎟
⎠
⎞
⎜
⎝
⎛
−+−=
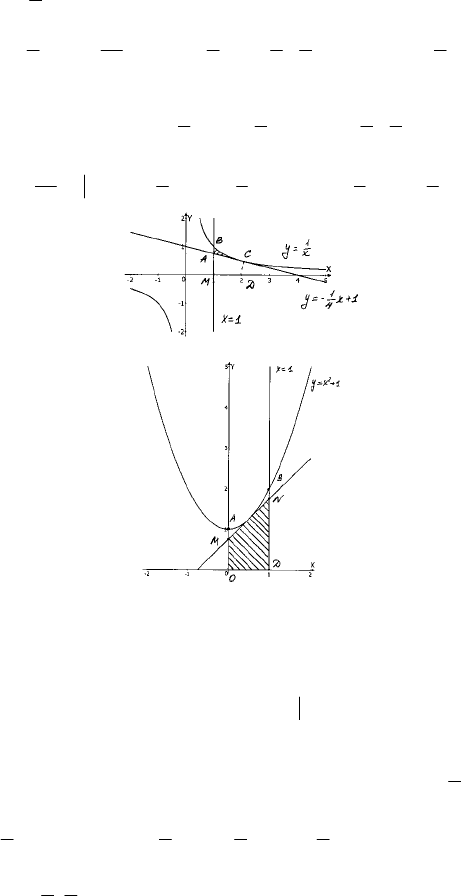
4) у = х
3
; у = 1; x = –2
ABCO — искомая фигура,
S
ABCО
= S
DBCO
+ S
ADO
,;
S
DBCO
= S
DBKO
+ S
KOC
; S
DBKO
= 2 ⋅ 1;
4
3
4
1
1
4
111
1
0
4
1
0
3
=−=−=−⋅=−=
∫
x
dxxSSS
OCMOKCMKOC
Теперь рассмотрим фигуру, симметричную ADO – A
1
DO:
4
4
16
0
4
0
2
4
0
2
3
1
=+=−=−==
−
−
∫
x
dxxSS
DOAADO
S
ABCО
= 2 +
4
3
+ 4 = 6
4
3
.

122
№ 1023
1) у = х
2
+ 10; (0; 1).
Уравнение касательной у = kx + b
(0; 1); 1 = k ⋅ 0 + b, b = 1, у = kх + 1
у = f (х
0
) + k (x – x
0
), где х
0
– точка касания
у =
2
0
x + 10 + kx – kх
0
, значит: kx + 1 =
2
0
x + 10 + kx – kх
0
2
0
x – kх
0
+ 9 = 0, но k = f ′(х
0
) = 2х
0
2
0
x – 2
2
0
x + 9 = 0 9 –
2
0
x = 0 х
0
= ± 3
Т.е. k = ± 6 y = 6x + 1 y = –6x + 1
ABCD – искомая фигура.
()
(
)
()
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+−+=−==
∫∫
3
0
3
0
2
1610222 dxxdxxSSSS
OADNOCDNACDABCD
()
()
1827279293
3
2962
3
0
2
3
3
0
2
=+−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+−=+−=
∫
xx
x
dxxx .
123
2) у =
x
1
; х = 1, и касат. х
0
= 2
у(х
0
) =
2
1
, у′ =
2
1
x
− , у′(х
0
) =
4
1
−
,
()
2
4
1
2
1
−−=
xy
,
1
4
1
+−=
xy
;
АВС – искомая фигура
=
⎟
⎠
⎞
⎜
⎝
⎛
−+=
⎟
⎠
⎞
⎜
⎝
⎛
+−−=−=
∫∫∫
2
1
2
1
2
1
1
4
11
1
4
11
dxx
x
dxxdx
x
SSS
MACDMBCDABC
8
5
2ln
8
3
12ln1
8
1
02
2
1
2ln
8
ln
2
1
2
−=+−=+−−−+=−+= x
x
x .
№ 1024
у = х
2
+1; у = 0; х = 0; х = 1
1) Уравнение касательной: у = f (х
0
) – f ′(х
0
) (х – х
0
), у = у
0
+ 2х
0
(х – х
0
),
у = 2х
0
⋅ х +
2
0
x – 2
2
0
x + 1, у = 2х
0
⋅ х –
2
0
x + 1;
2) OMND – искомая трапеция
()
0112
2
00
1
0
2
0
2
0
1
0
2
00
−+−=+−=+−=
∫
xxxxxxxdxxxxS
OMND
Найдем наибольшее значение функции на (0; 1).
f (х) = –х
2
+ х + 1, f ′(х) = –2х + 1, f ′(х) = 0, 2х – 1 = 0, х =
2
1
,
х =
2
1
– точка max., х
0
=
2
1
, у
0
=
4
1
11
2
1
2
=+
⎟
⎠
⎞
⎜
⎝
⎛
.
Ответ:
⎟
⎠
⎞
⎜
⎝
⎛
4
5
;
2
1
.
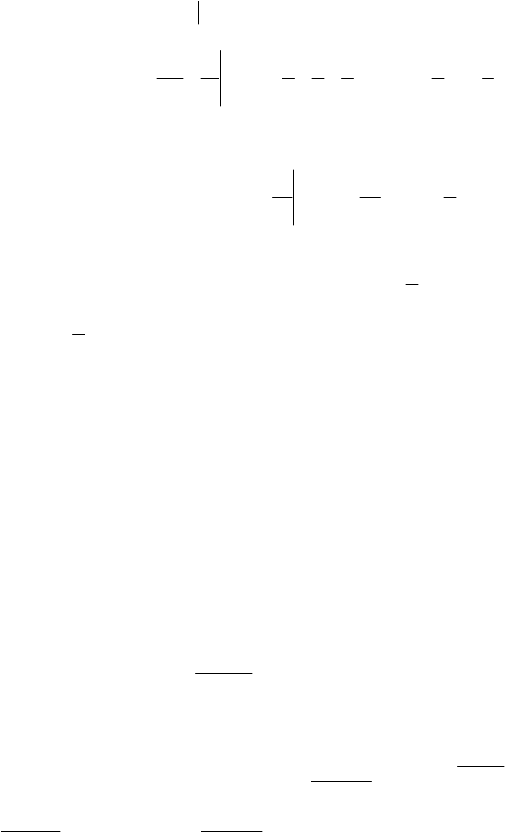
124
§ 59 Применение производной и интеграла
к решению практических задач
№ 1025
v(t) = s′(t), s – первообразная v(t)
1)
()
()
6846413
4
0
3
4
0
2
=+=+=+=
∫
ttdttts ;
2)
()
()
3
1
21
3
2
418
2
1
3
2
2
9
18
23
2
2
3
1
23
3
1
2
=−+=−−+=+=+=
∫
tt
dtttts .
№ 1026
1) v(t) = 0, 4t – t
2
= 0, t = 0, t = 4;
2)
() ()
()
3
2
100
3
64
32
3
24
4
0
3
2
4
0
2
2
1
=−−=−=−==
∫∫
t
tdtttdttvts
t
t
.
№ 1027
1) у = 3х – 2х
2
+ С; 2) у = 2х
3
– 4х
2
+ х + С; 3)
Cey
x
+=
2
2
3
;
4)
CxCxy +=+⋅⋅= 2sin22sin
2
1
4
.
5) у = 3 ⋅ (–cos х) + С = –3cos х + С; 6) у = sin x + cos x + C.
№ 1028
1) у = –cos x + C; –cos 0 + C = 0, C = 1, y = –cos x + 1
2) у = 2sin x + C; 2sin π + C = 1, C = 1, y = 2sin x + 1
3) у = x
3
+ 2x
2
– x + C; 1 + 2 – 1 + C = –2, C = –4; y = x
3
+ 2x
2
– x – 4
4) у = 2x + x
2
– x
3
+ C; –2 + 1 + 1 + C = 2, C = 2; у = 2x + x
2
– x
3
+ 2
5) у = e
x
+ C; e + C = 1, C = 1 – e, y = e
x
+ 1 – e
6) у = –e
–x
+ C; –1 + C = 2 C = 3 y = –e
–x
+ 3.
№ 1029
y′ = –С
1
ωsin ωx + С
2
ωcos ωx; y′′ = –С
1
ω
2
cos ωx – С
2
ω
2
sin ωx;
y′′ + ω
2
у = –С
1
ω
2
cos ωx – С
2
ω
2
sin ωx + ω
2
С
1
cos ωx + ω
2
С
2
sin ωx = 0;
0 = 0 – верно при любых С
1
и С
2
.
№ 1030
Скорость распада m′(t) =
л10
г001,0
=0,0001
m′(t) = k m (t) решение m(t) = m
0
e
–kt
В нашем случае m′(t)=0,0001 и m
0
=1, t=10, m(t) = 0,999, 0,999=1⋅ e
–10k
e
–10k
= 0,999, –10k = ln 0,999,
10
999,0ln
−=k ,
t
e
⋅
⋅=
10
999,0ln
15,0,
5,0ln
10
999,0ln
=⋅ t
,
999,0ln
5,0ln10
=
t , t ≈ 6928.
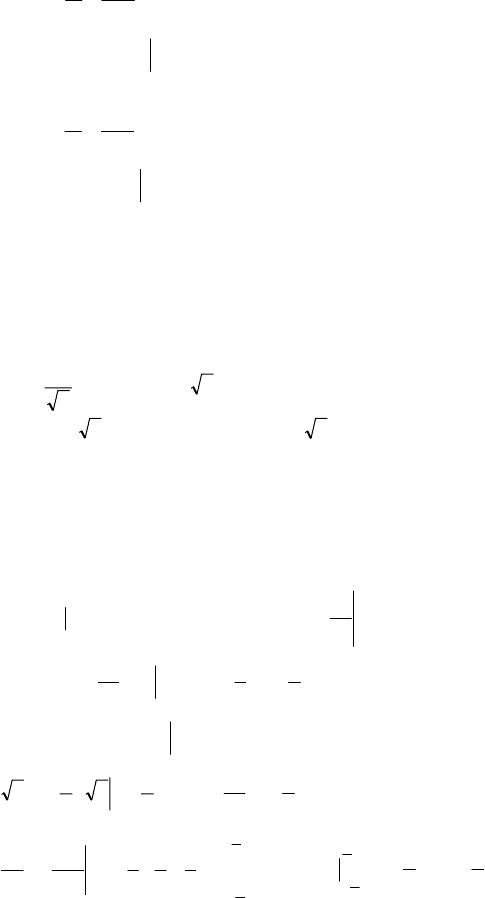
125
№ 1031
F = kx;
2
01,0
2
===
x
F
k
, F = 200x
09,0009,0100200
03,0
0
03,0
0
2
=−===
∫
xxdxA Дж.
№ 1032
F = kx, 300
01,0
3
===
x
F
k
, F = 300x
96,0150300
08,0
0
2
08,0
0
===
∫
xxdxA Дж.
Упражнения к главе Х
№ 1033
1) f (x) = cos x, тогда F(x) = sin x + C
(0; –2): –2 = sin 0 + C, C = –2; F(x) = sin x – 2
2) f (x) = sin x, тогда F(x) = –cos x + C
(–π; 0): 0 = –cos (–π) + C, C = –1; F(x) = –cos x – 1.
3) f (x) =
x
1
, тогда F(x) =
x2+ C
(4; 5): 5 =
42+ C , C = 1; F(x) = x2+ 1
4) f (x) = e
x
, тогда F(x) = e
x
+ C
(0; 2): 2 = 1 + C, C = 1; F(x) = e
x
+ 1.
5) f (x) = 3x
2
+ 1, тогда F(x) = x
3
+ x + C
(1; –2): –2 = 1 + 1 + C, C = –4; F(x) = x
3
+ x – 4
6) f (x) = 2 – 2x, тогда F(x) = 2x – x
2
+ C
(2; 3): 3 = 4 – 4 + C, C = 3; F(x) = 2x – x
2
+ 3.
№ 1034
1) 62422
2
1
2
1
=+==
−
−
∫
xdx ; 2)
()
122626
2
33
2
2
2
2
2
=++−=−=−
−
−
∫
x
xdxx ;
3)
()
3
2
1
3
1
99
3
2
3
1
2
3
3
1
2
=+−−=−=−
∫
x
x
dxxx ;
4)
()
2111132
1
1
32
1
1
2
−=−−−=−=−
−
−
∫
xxdxxx
;
5)
()
4
1
11
4
45
116
4
3
4
3
8
1
3
8
1
3
==−==
∫
xxdxx ;
6)
8
3
2
1
8
1
2
1
8
1
2
2
1
3
=+−=−=
∫
xx
dx
; 7)
2
2
sin
2
sinsincos
2
2
2
2
=
⎟
⎠
⎞
⎜
⎝
⎛
π
−−
π
==
π
π
−
π
π
−
∫
xxdx
.
126
№ 1035
1) у = x ; х = 1; х = 4; у = 0
АВСD – искомая фигура
()
3
2
4
3
14
18
3
2
3
2
4
1
4
1
==−===
∫
xxdxxS
ABCD
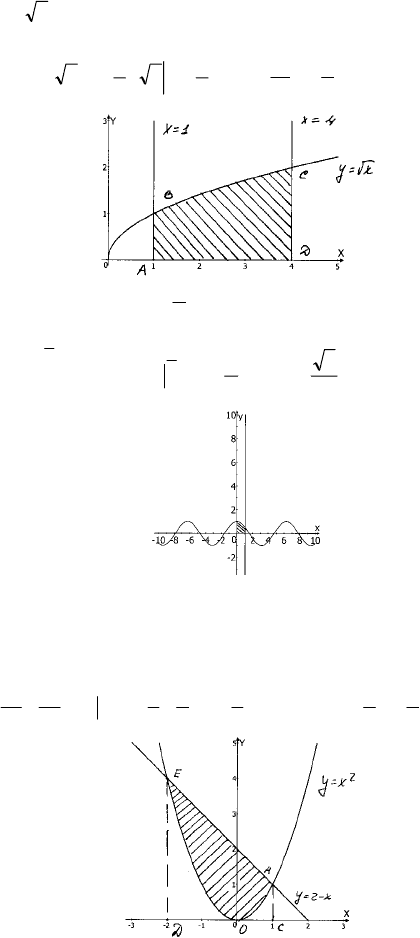
2) у = cos x х = 0 х =
3
π
у = 0; OАВС – искомая фигура;
2
3
0sin
3
sinsincos
3
0
3
0
=−
π
===
π
π
∫
xxdxS
OABC
;
3) у = x
2
; у = 2 – х, х
2
= 2 – х, х
2
+ х – 2 = 0, х
1
= –2, х
2
= 1,
ЕОА – искомая фигура
()
(
)
=+−−=−−=−=
∫∫∫
−−−
1
2
2
1
2
2
1
2
22 dxxxdxxdxxSSS
EDOACDEACEOA
2
1
4
2
1
3842
3
8
2
2
1
3
1
2
23
1
2
23
=−−=++−+−−=+−−=
−
x
xx
127
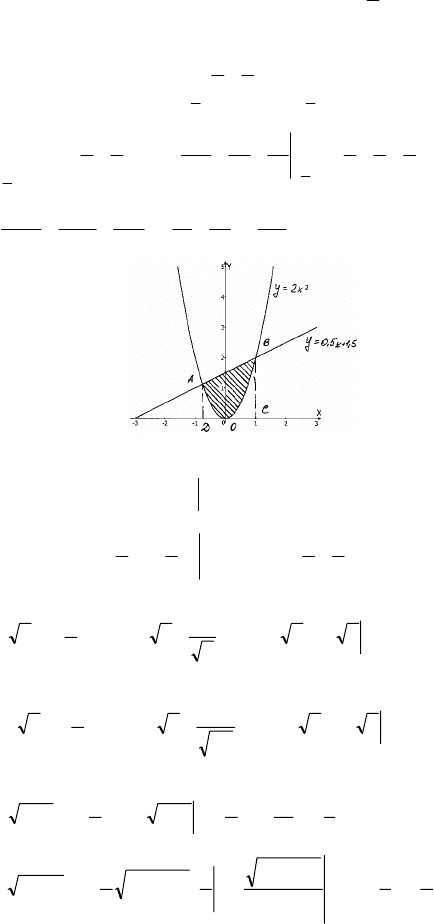
4) у = 2x
2
; у = 0,5х + 1,5; 2х
2
= 0,5х + 1,5,
4х
2
– х – 3 = 0; D = 1 + 48 = 49, х
1
= 1 х
2
=
4
3
−
,
АОВ – искомая фигура,
=−
⎟
⎠
⎞
⎜
⎝
⎛
+=−=
∫∫
−−
1
4
3
2
1
4
3
2
2
3
2
dxxdx
x
SSS
DAOBCDABCAOB
−++−=++−=
⎟
⎠
⎞
⎜
⎝
⎛
++−=
−
−
∫
2
3
4
1
3
2
2
3
43
2
2
3
2
2
1
4
3
23
1
4
3
2
xxx
dx
x
x
192
151
1
64
45
12
13
42
33
416
9
643
272
=+=
⎟
⎠
⎞
⎜
⎝
⎛
⋅
⋅
−
⋅
+
⋅
⋅
− .
№ 1036
1)
()
121285
1
0
45
1
0
34
−=−=−=−
∫
xxdxxx ;
2)
()
15
2
5
2
3
1024
2
5
2
3
56
2
1
24
2
1
3
=+−−=−=−
−
−
∫
xxdxxx
(опечатка в ответе задачника)
3)
=−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
⎟
⎠
⎞
⎜
⎝
⎛
−
∫∫
4
1
4
1
4
1
142
7
3
7
3 xxxdx
x
xdx
x
x
01422816 =+−−= ;
4)
=−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
⎟
⎠
⎞
⎜
⎝
⎛
−
∫∫
8
1
33
8
1
3
2
3
8
1
3
483
16
4
4
14 xxxdx
x
xdx
x
x
34839648
−
=+−−= ;
5)
()
3
1
5
3
16
8
3
2
11
3
2
1
3
0
3
0
==⋅=++=+
∫
xxdxx
;
6)
()
()
3
2
8
3
1
9
3
32
2
1
32
3
2
32
6
2
3
6
2
3
6
2
=−=
−
=⋅−=−
∫
x
xdxx .

128
№ 1037
1)
=
⎟
⎠
⎞
⎜
⎝
⎛
π
−
π
=
⎟
⎠
⎞
⎜
⎝
⎛
π
+=
⎟
⎠
⎞
⎜
⎝
⎛
π
+
π
π
∫
4
sin
2
sin
2
1
4
sin
2
1
4
cos
2
1
4
0
4
0
xdxx
4
22
2
2
1
2
1 −
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−= ;
2)
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
π
−−−=
⎟
⎠
⎞
⎜
⎝
⎛
π
−−=
⎟
⎠
⎞
⎜
⎝
⎛
π
−
π
π
∫
3
cos0cos
3
1
3
cos
3
1
3
sin
3
1
3
0
3
0
xdxx
6
1
2
1
1
3
1
−=
⎟
⎠
⎞
⎜
⎝
⎛
−−= ;
3)
() () () ()
=−++−=−⋅−=−
∫
3cos3cos63cos163sin3
3
1
3
1
xdxx
03cos3cos =+−= ;
4)
() () ()()
=−−=−=−
∫
12sin0sin2124sin2124cos8
3
0
3
0
xdxx
()
12sin212sin02 =+= .
№ 1038
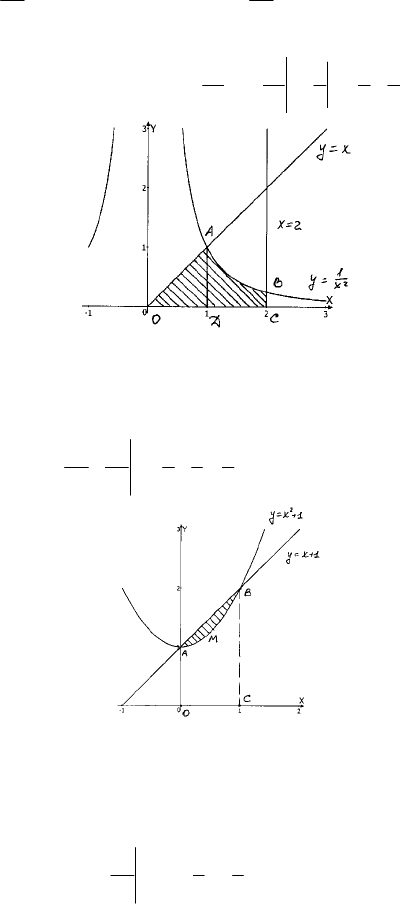
1) у =
x
1
; у = 4х; х = 1; у = 0,
x
1
=4х, 4х
2
= 1, х =
2
1
±
.
ОАВС – искомая фигура
=+=+=+=
∫∫
1
2
1
2
1
0
2
1
2
1
2
1
0
ln2
1
4 xxdx
x
xdxSSS
DABCOADOABC
2
1
ln
2
1
2
1
ln1ln
2
1
−=⋅+=
;
129
2)
у =
2
1
x
; у = х; х = 2; у = 0;
2
1
x
= х, х
3
= 1, х = 1.
ОАВС – искомая фигура
11
2
1
2
11
2
1
2
1
1
0
2
2
1
2
1
0
=+−=−=+=+=
∫∫
x
x
dx
x
xdxSSS
DABCOADOABC
.
3)
у = х
2
+ 1; у = х + 1, х
2
+ 1 = х + 1, х
2
– х = 0, х
1
= 0, х
2
= 1
АМВ – искомая фигура
()
(
)
(
)
∫∫∫
=−−+=+−+=−=
1
0
2
1
0
2
1
0
1111 dxxxdxxdxxSSS
OAMBCOABCAMB
()
6
1
3
1
2
1
32
1
0
32
1
0
2
=−=−=−=
∫
xx
dxxx ;
4) у = х
2
+ 2; у = 2х + 2
х
2
+ 2 = 2х + 2, х
2
– 2х = 0, х
1
= 0, х
2
= 2
АМВ – искомая фигура
()
(
)
=+−+=−=
∫∫
2
0
2
2
0
222 dxxdxxSSS
OAMBCOABCAMB
()
3
1
1
3
8
4
3
2
2
0
3
2
2
0
2
=−=−=−=
∫
x
xdxxx .
