Jost J. Partial Differential Equations
Подождите немного. Документ загружается.

Exercises 217
8.2 What would be a natural definition of k-times weak differentiablity? (The
answer will be given in the next chapter, but you might wish to try
yourself at this point to define Sobolev spaces W
k,2
(Ω)ofk-times weakly
differentiably functions that are contained in L
2
(Ω) together with all
their weak derivatives and to prove results analogous to Theorem 8.2.1
and Corollary 8.2.1 for them.)
8.3 Consider a variational problem of the type
I(u)=
Ω
F (Du(x))dx
with a smooth function F : R
d
→ Ω satisfying an inequality of the form
|F (p)|≤c
1
|p|
2
+ c
2
for all p ∈ R
d
.
Derive the corresponding Euler–Lagrange equations for a minimizer (in
the weak sense; cf. (8.4.4)). Try more generally to find conditions for
integrands of the type F (x, u(x),Du(x)) that allow one to derive weak
Euler–Lagrange equations for minimizers.
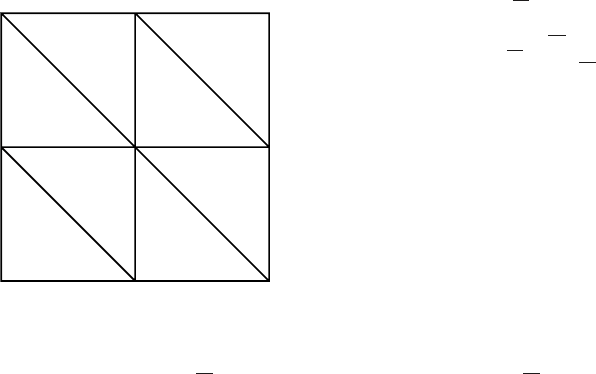
8.4 Following R. Courant, as a model problem for finite elements we consider
the Poisson equation
Δu = f in Ω,
u =0 on∂Ω
Figure 8.1.
in the unit square Ω =[0, 1] ×
[0, 1] ⊂ R
2
.Forh =
1
2
n
(n ∈
N), we subdivide
Ω into
1
h
2
(=
2
2n
) subsquares of side length h,
andeachsuchsquareinturnis
subdivided into two right-angled
symmetric triangles by the di-
agonal from the upper left to
the lower right vertex (see Fig-
ure 8.1). We thus obtain trian-
gles Δ
h
i
,i=1,...,2
2n+1
.What
is the number of interior vertices
p
j
of this triangulation?
We consider the space of continuous triangular finite elements
S
h
:= {ϕ ∈ C
0
(Ω):ϕ
|Δ
h
i
linear for all i, ϕ =0on∂Ω}.
The triangular elements ϕ
j
with
ϕ
j
(p
i
)=δ
ij

218 8. Existence Techniques III
constitute a basis of S
h
(proof?).
Compute
a
ij
:=
Ω
Dϕ
i
· Dϕ
j
for all pairs i, j
and establish the system of linear equations for the approximating solu-
tion of the Poisson equation in S
h
, i.e., for the minimizer ϕ
h
of
Ω
|Dϕ|
2
+2
Ω
fϕ
for ϕ ∈ S
h
, with respect to the above basis ϕ
j
of S
h
(for that purpose,
you have just computed the coefficients a
ij
!).

9. Sobolev Spaces and L
2
Regularity Theory
9.1 General Sobolev Spaces. Embedding Theorems of
Sobolev, Morrey, and John–Nirenberg
Definition 9.1.1: Let u : Ω → R be integrable, α := (α
1
,...,α
d
),
D
α
ϕ :=
∂
∂x
1
α
1
···
∂
∂x
d
α
d
ϕ for ϕ ∈ C
|α|
(Ω).
An integrable function v : Ω → R is called an αth weak derivative of u,in
symbols v = D
α
u,if
Ω
ϕv dx =(−1)
|α|
Ω
uD
α
ϕdx for all ϕ ∈ C
|α|
0
(Ω). (9.1.1)
For k ∈ N, 1 ≤ p<∞, we define the Sobolev space
W
k,p
(Ω):={u ∈ L
p
(Ω):D
α
u exists and is contained in L
p
(Ω) for
all |α|≤k},
u
W
k,p
(Ω)
:=
⎛
⎝
|α|≤k
Ω
|D
α
u|
p
⎞
⎠
1
p
.
The spaces H
k,p
(Ω) and H
k,p
0
(Ω) are defined to be the closures of C
∞
(Ω)
and C
∞
0
(Ω), respectively, with respect to ·
W
k,p
(Ω)
. Occasionally, we shall
employ the abbreviation ·
p
= ·
L
p
(Ω)
.
Concerning notation: The multi-index notation will be used in the present
section only. Later on, for u ∈ W
1,p
(Ω), first weak derivatives will be denoted
by D
i
u, i =1,...,d, as in Definition 8.2.1, and we shall denote the vector
(D
1
u,...,D
d
u)byDu. Likewise, for u ∈ W
2,p
(Ω), second weak derivatives
will be written D
ij
u, i, j =1,...,d, and the matrix of second weak derivatives
will be denoted by D
2
u.
As in Section 8.2, one proves the following lemma:
Lemma 9.1.1: W
k,p
(Ω)=H
k,p
(Ω). The space W
k,p
(Ω) is complete with
respect to ·
W
k,p
(Ω)
, i.e., it is a Banach space.

220 9. Sobolev Spaces and L
2
Regularity Theory
We now state the Sobolev embedding theorem:
Theorem 9.1.1:
H
1,p
0
(Ω) ⊂
L
dp
d−p
(Ω) for p<d,
C
0
(
¯
Ω) for p>d.
Moreover, for u ∈ H
1,p
0
(Ω) ,
u
dp
d−p
≤ c Du
p
for p<d, (9.1.2)
sup
Ω
|u|≤c |Ω|
1
d
−
1
p
·Du
p
for p>d, (9.1.3)
where the constant c depends on p and d only.
In order to better understand the content of the Sobolev embedding the-
orem, we first consider the scaling behavior of the expressions involved: Let
f ∈ H
1,p
(R
d
) ∩ L
q
(R
d
). We look at the scaling y = λx (with λ>0) and
f
λ
(y):=f
y
λ
= f(x).
Then, with y = λx,
R
d
|Df
λ
(y)|
p
dy
1
p
= λ
d−p
p
R
d
|Df(x)|
p
dx
1
p
(note that on the left, the derivative is taken with respect to y, and on the
right with respect to x; this explains the −p in the exponent) and
R
d
|f
λ
(y)|
q
dy
1
q
= λ
d
q
R
d
|f(x)|
q
dx
1
q
.
Thus in the limit λ → 0, f
λ
L
q
is controlled by Df
λ
L
p
if
λ
d
q
≤ λ
d−p
p
for λ<1
holds, i.e.,
d
q
≥
d − p
p
,
i.e.,
q ≤
dp
d − p
if p<d.
(We have implicitly assumed Df
L
p
> 0 here, but you will easily convince
yourself that this is the essential case of the embedding theorem.) We treat
only the limit λ → 0 here, since only for λ ≤ 1(forf ∈ H
1,p
0
(R
d
)) do we have
9.1 General Sobolev Spaces. Embedding Theorems 221
supp f
λ
⊂ supp f,
and the Sobolev embedding theorem covers only the case where the functions
have their support contained in a fixed bounded set Ω. Looking at the scaling
properties for λ →∞, one observes that this assumption on the support is
necessary for the theorem. The scaling properties for p>dwill be examined
after Corollary 9.1.5.
Proof of Theorem 9.1.1: We shall first prove the inequalities (9.1.2) and
(9.1.3) for u ∈ C
1
0
(Ω). We put u =0onR
d
\ Ω again. As in the proof
of Theorem 8.2.2,
|u(x)|≤
x
i
−∞
|D
i
u(x
1
,...,x
i−1
,ξ,x
i+1
,...,x
d
)|dξ with x =(x
1
,...,x
d
)
for 1 ≤ i ≤ d, and hence
|u(x)|
d
≤
d
!
i=1
∞
−∞
|D
i
u|dx
i
and
|u(x)|
d
d−1
≤
d
!
i=1
∞
−∞
|D
i
u|dx
i
1
d−1
.
It follows that
∞
−∞
|u(x)|
d
d−1
dx
1
≤
∞
−∞
|D
1
u|dx
1
1
d−1
!
i=1
∞
−∞
∞
−∞
|D
i
u|dx
i
dx
1
1
d−1
,
wherewehaveused(A.6)forp
1
= ···= p
d−1
= d − 1. Iteratively, we obtain
Ω
|u(x)|
d
d−1
dx ≤
d
!
i=1
Ω
|D
i
u|dx
1
d−1
,
and hence
u
d
d−1
≤
d
!
i=1
Ω
|D
i
u|dx
1
d
≤
1
d
Ω
d
i=1
|D
i
u|dx,
since the geometric mean is not larger than the arithmetic one, and conse-
quently
u
d
d−1
≤
1
d
Du
1
, (9.1.4)
222 9. Sobolev Spaces and L
2
Regularity Theory
which is (9.1.2) for p =1.
Applying (9.1.4) to |u|
γ
(γ>1) (|u|
γ
is not necessarily contained in
C
1
0
(Ω), even if u is, but as will be explained at the end of the present proof,
by an approximation argument, if shown for C
1
0
(Ω), (9.1.4) continues to hold
for H
1,1
0
, and we shall choose γ such that for u ∈ H
1,p
0
(Ω), we have |u|
γ
∈
H
1,1
0
(Ω)), we obtain
|u|
γ
d
d−1
≤
γ
d
Ω
|u|
γ−1
|Du|dx ≤
γ
d
)
)
)
|u|
γ−1
)
)
)
q
·Du
p
for
1
p
+
1
q
=1
(9.1.5)
applying H¨older’s inequality (A.4). For p<d, γ =
(d−1)p
d−p
satisfies
γd
d − 1
=
(γ −1)p
p − 1
,
and (9.1.5) yields, taking q =
p
p−1
into account,
u
γ
γd
d−1
≤
γ
d
u
γ−1
γd
d−1
·Du
p
,
i.e.,
u
γd
d−1
≤
γ
d
Du
p
,
which is (9.1.2). In order to establish (9.1.3), we need the following general-
ization of Lemma 8.2.4:
Lemma 9.1.2: For μ ∈ (0, 1], f ∈ L
1
(Ω) let
(V
μ
f)(x):=
Ω
|x − y|
d(μ−1)
f(y)dy.
Let 1 ≤ p ≤ q ≤∞,
0 ≤ δ =
1
p
−
1
q
<μ.
Then V
μ
maps L
p
(Ω) continuously to L
q
(Ω),andforf ∈ L
p
(Ω), we have
V
μ
f
q
≤
1 − δ
μ − δ
1−δ
ω
1−μ
d
|Ω|
μ−δ
f
p
. (9.1.6)
Proof: Let
1
r
:= 1 +
1
q
−
1
p
=1−δ.
9.1 General Sobolev Spaces. Embedding Theorems 223
Then
(x − y):=|x − y|
d(μ−1)
∈ L
r
(Ω),
andasintheproofofLemma8.2.4,wechooseR such that |Ω| = |B(x, R)| =
ω
d
R
d
, and we estimate as follows:
r
=
Ω
|x − y|
d(μ−1)
1−δ
dy
1−δ
≤
B(x,R)
|x − y|
d(μ−1)
1−δ
dy
1−δ
=
1 − δ
μ − δ
1−δ
ω
1−δ
d
R
d(μ−δ)
=
1 − δ
μ − δ
1−δ
ω
1−μ
d
|Ω|
μ−δ
.
We write
|f | =
r(1−1/p)
(
r
|f|
p
)
1
q
|f|
pδ
,
and the generalized H¨older inequality (A.6) yields
|V
μ
f(x)|
≤
Ω
r
(x − y) |f(y)|
p
dy
1
q
Ω
r
(x − y)dy
1−
1
p
Ω
|f(y)|
p
dy
δ
;
hence, integrating with respect to x and interchanging the integrations in the
first integral, we obtain
V
μ
f
q
≤ sup
Ω
r
(x − y)dy
1
r
f
p
≤
1 − δ
μ − δ
1−δ
ω
1−μ
d
|Ω|
μ−δ
f
p
by the above estimate for
r
.
In order to complete the proof of Theorem 9.1.1, we use (8.2.4), assuming
first u ∈ C
1
0
(Ω) as before, i.e.,
u(x)=
1
dω
d
Ω
d
i=1
(x
i
− y
i
)
|x − y|
d
D
i
u(y)dy (9.1.7)
for x ∈ Ω. This implies
|u|≤
1
dω
d
V
1
d
(|D|). (9.1.8)

224 9. Sobolev Spaces and L
2
Regularity Theory
Inequality (9.1.6) for q = ∞, μ =1/d then yields (9.1.3), again at this
moment for u ∈ C
1
0
(Ω)only.
If now u ∈ H
1,p
0
(Ω), we approximate u in the W
1,p
-norm by C
∞
0
functions
u
n
, and apply (9.1.2) and (9.1.3) to the difference u
n
− u
m
. It follows that
(u
n
) is a Cauchy sequence in L
dp/(d−p)
(Ω)(forp<d)orC
0
(
¯
Ω)(forp>d),
respectively. Thus u itself is contained in the same space and satisfies (9.1.2)
or (9.1.3), respectively
Corollary 9.1.1:
H
k,p
0
(Ω) ⊂
L
dp
d−kp
(Ω) for kp < d,
C
m
(Ω) for 0 ≤ m<k−
d
p
.
.
Proof: The first embedding iteratively follows from Theorem 9.1.1, and the
second one then from the first and the case p>din Theorem 9.1.1.
Corollary 9.1.2: If u ∈ H
k,p
0
(Ω) for some p and all k ∈ N, then u ∈
C
∞
(Ω).
The embedding theorems to follow will be used in Chapter 12 only. First
we shall present another variant of the Sobolev embedding theorem. For a
function v ∈ L
1
(Ω), we define the mean of v on Ω as
−
Ω
v(x)dx :=
1
|Ω|
Ω
v(x)dx,
|Ω| denoting the Lebesgue measure of Ω. We then have the following result:
Corollary 9.1.3: Let 1 ≤ p<dand u ∈ H
1,p
(B(x
0
,R)). Then
−
B(x
0
,R)
|u|
dp
d−p
d−p
dp
≤ c
0
R
p
−
B(x
0
,R)
|Du|
p
+ −
B(x
0
,R)
|u|
p
1
p
, (9.1.9)
where c
0
depends on p and q only.
Proof: Without loss of generality, x
0
= 0. Likewise, we may assume R =
1, since we may consider the functions ˜u(x)=u(Rx) and check that the
expressions in (9.1.9) scale in the right way. Thus, let u ∈ H
1,p
(B(0, 1)). We
extend u to the ball B(0, 2), by putting
u(x)=u
x
|x|
2
for |x| > 1.
This extension satisfies
u
H
1,p
(B(0,2))
≤ c
1
u
H
1,p
(B(0,1))
. (9.1.10)

9.1 General Sobolev Spaces. Embedding Theorems 225
Now let η ∈ C
∞
0
(B(0, 2)) with
η ≥ 0,η≡ 1onB(0, 1), |Dη|≤2.
Then v = ηu ∈ H
1,p
0
(B(0, 2)), and by (9.1.2),
B(0,2)
|v|
dp
d−p
d−p
dp
≤ c
2
B(0,2)
|Dv|
p
1
p
. (9.1.11)
Since
Dv = ηDu + uDη,
from the properties of η, we deduce
|Dv|
p
≤ c
3
(|Du|
p
+ |u|
p
) , (9.1.12)
and hence with (9.1.10),
B(0,2)
|Dv|
p
≤ c
4
B(0,1)
|Du|
p
+
B(0,1)
|u|
p
. (9.1.13)
Since on the other hand
B(0,1)
|u|
dp
d−p
≤
B(0,2)
|v|
dp
d−p
,
(9.1.9) follows from (9.1.11) and (9.1.13).
Later on (in Section 12.1), we shall need the following result of John and
Nirenberg:
Theorem 9.1.2: Let B(y
0
,R
0
) be a ball in R
d
, u ∈ W
1,1
(B(y
0
,R
0
)),and
suppose that for all balls B(y, R) ⊂ R
d
,
B(y,R)∩B(y
0
,R
0
)
|Du|≤R
d−1
. (9.1.14)
Then there exist α>0 and β
0
< ∞ satisfying
B(y
0
,R
0
)
e
α|u−u
0
|
≤ β
0
R
d
0
(9.1.15)
with
u
0
=
1
ω
d
R
d
0
B(y
0
,R
0
)
u (mean of u on B(y
0
,R
0
)).
In particular,
B(y
0
,R
0
)
e
αu
B(y
0
,R
0
)
e
−αu
=
B(y
0
,R
0
)
e
α(u−u
0
)
B(y
0
,R
0
)
e
−α(u−u
0
)
≤ β
2
0
R
2d
0
.
(9.1.16)

226 9. Sobolev Spaces and L
2
Regularity Theory
More generally, for a measurable set B ⊂ R
d
,andu ∈ L
1
(B), we denote
the mean by
u
B
:=
1
|B|
B
u(y)dy, (9.1.17)
|B| being the Lebesgue measure of B. In order to prepare the proof of The-
orem 9.1.2, we start with a lemma:
Lemma 9.1.3: Let Ω ⊂ R
d
be convex, B ⊂ Ω measurable with |B| > 0,
u ∈ W
1,1
(Ω). Then we have for almost all x ∈ Ω,
|u(x) − u
B
|≤
(diam Ω)
d
d |B|
Ω
|x − z|
1−d
|Du(z)|dz. (9.1.18)
Proof: As before, it suffices to prove the inequality for u ∈ C
1
(Ω). Since Ω
is convex, if x and y are contained in Ω, so is the straight line joining them,
and we have
u(x) − u(y)=−
|x−y|
0
∂
∂r
u
x + r
y − x
|y − x|
dr,
and thus
u(x) − u
B
=
1
|B|
B
(u(x) − u(y))dy
= −
1
|B|
B
|x−y|
0
∂
∂r
u
x + r
y − x
|y − x|
dr dy.
This implies
|u(x) − u
B
|≤
1
|B|
(diam Ω)
d
d
|ω|=1
x+rω∈Ω
|x−y|
0
∂
∂r
u(x + rω)dr dω
, (9.1.19)
if instead of over B, we integrate over the ball B(x, diam Ω)) ∩ Ω,write
dy =
d−1
dω d in polar coordinates, and integrate with respect to .Thus,
as in the proofs of Theorems 1.2.1 and 8.2.2,
|u(x) − u
B
|≤
1
|B|
(diam Ω)
d
d
|x−y|
0
∂B(x,r)∩Ω
1
r
d−1
∂u
∂ν
(z)dσ(z)dr
=
1
|B|
(diam Ω)
d
d
Ω
1
|x − z|
d−1
d
i=1
∂
∂z
i
u(z)
x
i
− z
i
|x − z|
dz
≤
(diam Ω)
d
d |B|
Ω
1
|x − z|
d−1
|Du(z)|dz.
