Jeevanjee N. An Introduction to Tensors and Group Theory for Physicists

Подождите немного. Документ загружается.

214 6 The Wigner–Eckart Theorem and Other Applications

SO(3)-invariant subspace (under the representation 

) that is actually equivalent

to the vector representation of SO(3)! This is an important shift in perspective, as we

are now thinking of the space of operators as a representation space, and of the

as spanning an invariant subspace of this space. This point of view has some

advantages, and is the one that will be formalized shortly in the notion of a repre-

sentation operator. Now, to verify that the deﬁnition (6.1) is equivalent to our earlier

deﬁnition of a vector operator from Chap. 3, you should check that if we perform

our usual trick and set R =e

and differentiate at t =0, as well as identify iπ(L

)

with what we have called the total angular momentum operator J

, we obtain

]=i



k=1



ij k

(6.2)

which is just (3.70).

Now, in physics texts one usually deﬁnes tensor operators similarly, i.e. as a set

of operators T

(r)

(s)

={T

...i

...j

} that under the representation 

of SO(3) trans-

form like the basis vectors e

⊗···⊗e

⊗ e

⊗···⊗e

of the space T

Again, this can be alternately formulated as saying that Span{T

...i

...j

}⊂L(H)

is an invariant subspace equivalent to the T

) representation of SO(3).Wehave

seen, though, that tensor product spaces such as T

) are usually decomposable,

so it is sometimes advantageous to consider spherical tensors of degree l, which

are sets of 2l +1 operators T

(l)

={T

(l)

}

0≤k≤2l

that under 

transform as the basis

vectors v

of the irreducible representation space V

, l ∈ Z.

Again, we will ﬁnd it

useful to think about Span{T

(l)

} as an invariant subspace of L(H) equivalent to V

rather than focusing on how the individual elements T

(l)

transform. Note that the

‘l’ in the superscript of T

(l)

is in parentheses; this is because the l is not really an

active index, but just serves to remind us which SO(3) representation we are dealing

with. (As an additional side note, the term ‘spherical tensor’ derives from the fact

that the representation V

,l ∈Z is equivalent to the space

of spherical harmonics

of degree l.)

The following example will help make the foregoing concrete.

Example 6.1 Product of vector operators

Consider two vector operators A ={A

}

i=1,2,3

and B ={B

}

j=1,2,3

on some Hilbert

space H with SO(3) representation . We can form a tensor operator (of type (0, 2))

by considering the set of their products AB ={A

}, i, j = 1, 2, 3. Each A

a linear operator on H, and it is easy to verify that AB is a bona ﬁde (0, 2) tensor

operator:

Warning: In other texts, different normalization and indexing conventions are used for the speciﬁc

basis vectors whose transformation properties the spherical tensors are supposed to mimic. In most

quantum mechanics texts, for instance, the components of a spherical tensor are supposed to mimic

the transformation properties of the kets |l,m which have different labeling and normalization

conventions than our v

, even though they are essentially the same thing.

6.1 Tensor Operators, Spherical Tensors and Representation Operators 215

(R)A

(R)

−1



(R)A

(R)

−1



(R)B

(R)

−1





k,l=1

(6.3)

which is the same as the usual transformation law for the basis vectors {e

⊗e

} of

). Thus, the nine-dimensional space Span{A

} is equivalent to T

) as

an SO(3) representation! We know, however, that T

) is reducible, and so then

(

, Span{A

}) must be reducible as well. We can decompose Span{A

} into

irreducible subspaces just as we decomposed T

) = Rg ⊕ S



) ⊕

and we should correspondingly obtain spherical tensors of degrees 0, 1 and 2. Ex-

plicitly, the degree 0 subspace corresponding to g =



i=1

⊗e

yields a spherical

tensor T

(0)

with single element

(0)



i=1

which transforms as a scalar. The degree 1 spherical tensor T

(1)

corresponding to



has elements

(1)

=(A ×B)

+i(A ×B)

(1)

=−2(A ×B)

(1)

=−2



(A ×B)

−i(A ×B)



where notation like (A ×B)

is just shorthand for A

−A

. The appearance

of the cross product here shouldn’t be surprising, since the cross product is essen-

tially just a way of identifying a bivector (or antisymmetric tensor) in 

with a

vector in R

, cf. Example 3.29. The degree 2 spherical tensor T

(2)

corresponding to



) has elements

(2)

=(A

+iA

)(B

+iB

)

(2)

=−2A

+iB

) −2(A

+iA

(2)

=−4(A

−2A

)

(2)

=12A

+iB

) +12(A

+iA

(2)

=24(A

−iA

)(B

−iB

To convince yourself that these operators really do transform as claimed, it is use-

ful to compare the above expressions with the expressions for the v

for H

)

and H

) (you should have computed these earlier as the f

from Problem 2.2).

You should also convince yourself that the span of {A

} is equal to the span

The funny looking normalization factors and index convention come from our normalization and

indexing convention for the v

s, which, as noted above, differ from the conventions in the physics

literature.

216 6 The Wigner–Eckart Theorem and Other Applications

of T

(0)

, T

(1)

, and T

(2)

taken together, so that we have the decomposition of

(

, Span{A

}) into irreducibles as

Span{A

}=SpanT

(0)

⊕Span T

(1)

⊕Span T

(2)

One might also call this a “decomposition of {A

} into spherical tensors”. 

By now you may have noticed that the above deﬁnitions are somewhat unwieldy;

they rely on transformation properties of speciﬁc operators, and seem to rely too

heavily on those operators, since the span of those operators seems more signiﬁcant

than the operators themselves. To remedy this, we present the following deﬁnition,

which subsumes all of the foregoing deﬁnitions and also presents things in a more

basis-independent fashion: given a representation (

) of a group G on some

auxiliary vector space V

, as well as a unitary representation (, H) of G on some

Hilbert space H, we deﬁne a representation operator to simply be an intertwiner

between V

and L(H), or in other words a linear map ρ :V

→L(H) satisfying





(g)v



=(g)ρ(v)(g)

−1

∀g ∈G, v ∈V

. (6.4)

Note that in terms of maps between V

and L(H), this just says

ρ ◦

(g) =

(g) ◦ρ ∀g ∈G. (6.5)

What this deﬁnition is saying, roughly, is that we have a subspace ρ(V

) ⊂ L(H )

which, even though it is composed of operators acting on H, actually transforms like

the space V

under similarity transformations by the operators 

. Note that, strictly

speaking, the representation operator ρ is not itself an operator, but an intertwiner

between representations.

How does this deﬁnition subsume the previous ones? Let V

have a basis {e

};

then since ρ is linear, it is completely determined by its action on this basis, and

plugging a basis vector e

into (6.4) then yields

(g)ρ(e

)(g)

−1





(g)



ρ(e

). (6.6)

If we set ρ(e

) ≡B

, this becomes

(g)B

(g)

−1





(g)



. (6.7)

This, of course, just says that under the representation 

,theB

transform like

basis vectors of the representation (

), which was how we deﬁned vector op-

erators, tensor operators, and spherical tensors in the ﬁrst place! In fact, if we take

G =SO(3) and V

, then (6.7) becomes (writing the matrices of the fundamen-

tal representation with both indices down)

(R)B

(R)

−1



j=1

which is of course just (6.1). To get tensor operators or spherical operators, we of

course just have to take V

) or V

), respectively.

6.2 Selection Rules and the Wigner–Eckart Theorem 217

Fig. 6.1 Action of the orthogonal projection operator P :H →W

on a vector v ∈H

Before leaving this section, it is worth re-emphasizing the shift in viewpoint that

we have made: we have taken a representation (, H) of G on a Hilbert space

H and then used the induced representation (

, L(H)) to let G act on the space

of operators L(V ); this space (of operators!) may then break up into irreducible

components, and knowing what irrep an operator lives in may actually tells us quite

a bit about its action on vectors in H. In particular we get selection rules and the

Wigner–Eckart theorem, which are the subjects of the next section.

6.2 Selection Rules and the Wigner–Eckart Theorem

Now that we have deﬁned representation operators, we can go on to formulate the

fundamental selection rule from which the usual quantum mechanical selection rules

can be derived. Then we can state and prove the Wigner–Eckart theorem, which is

a kind of complement to the angular momentum selection rules. First, though, we

need the following fact, the proof of which we only sketch. The details are deferred

to the problems referenced below.

Proposition 6.1 Let W

and W

be ﬁnite-dimensional inequivalent irreducible sub-

spaces of a unitary representation (, H) equipped with an inner product (·|·).

Then W

is orthogonal to W

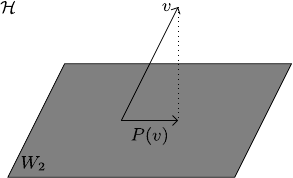
Proof sketch Deﬁne the orthogonal projection operator P :H →W

to be the map

which sends v ∈H to the unique vector P(v)∈W

satisfying



P(v)|w



=(v|w) ∀w ∈W

. (6.8)

This is depicted schematically in Fig. 6.1. You will check in Problem 6.1 that such

a vector P(v) exists and is in fact unique. If we now restrict P to W

we get

P |

: W

→ W

, and using the unitarity of  and the invariance of the W

one

can show that P |

is an intertwiner. One can then use Schur’s lemma to conclude

that P |

=0, which then implies that W

is orthogonal to W

. To ﬁll out the details,

see Problem 6.2. 

218 6 The Wigner–Eckart Theorem and Other Applications

With this in hand, we can now state and prove

Proposition 6.2 (Selection rule) Let G be a semi-simple group, and let W

and W

be ﬁnite-dimensional inequivalent irreducible subspaces of a unitary representation

(, H) of G. Also let ρ :V

→L(H) be a representation operator, where (

)

is some auxiliary representation. Then



|ρ(v)w



=0 ∀v ∈V

∈W

(6.9)

unless the decomposition of V

⊗ W

into irreducibles contains a representation

equivalent to W

Before proving this, let us comment on what this somewhat opaque proposition

really means. Roughly speaking, the selection rule just says that a vector of the form

ρ(v)w

is a kind of ‘product’ of elements of V

and W

, and thus transforms like

something in V

⊗W

⊕···⊕U

. Thus, for there to be any overlap with an

irreducible subspace W

, W

must then be equivalent to one of the U

Proof of proposition Deﬁne a map by

T :V

⊗W

→H

v ⊗w

→ ρ(v)w

(6.10)

and extending linearly to arbitrary elements of V

⊗W

. You can check that this is

a linear map between vector spaces, and so the image T(V

⊗W

) ≡ D ⊂ H is a

vector subspace of H. Now, since G is semi-simple we can decompose V

⊗ W

into irreducibles as

⊗W

⊕···⊕U

for some irreps U

. As you will show below, the fact that ρ is a representation

operator implies that T is in fact an intertwiner, and this further implies that the

kernel of T (cf. Exercise 4.17) is an invariant subspace of V

⊗W

. This means that

(with a possible relabeling of the U

) we can write the kernel of T as U

⊕···⊕U

for some m ≤ k, which then implies that D is equivalent to U

m+1

⊕···⊕U

.If

none of the U

are equivalent to W

, then by Proposition 6.1, every vector in D is

orthogonal to every vector in W

,i.e.



|ρ(v)w



=0 ∀v ∈V

∈W

which is what we wanted to prove. 

Exercise 6.1 Quickly show that ρ being a representation operator implies that T is an

intertwiner. Show further that the kernel of T is an invariant subspace of V

⊗W

We will now use this generalized selection rule to reproduce some of the familiar

selection rules from quantum mechanics.

6.2 Selection Rules and the Wigner–Eckart Theorem 219

Example 6.2 Parity selection rules

Let (, H) be a complex unitary representation of the two-element group Z

{I,P} where P is the parity operator. Let v

∈ H be parity eigenstates with

eigenvalues c

, c

.Ifc

=1 then v

spans the one-dimensional trivial representa-

tion of Z

, and if c

=−1 then v

spans the alternating representation. Likewise for

.NowletV

be another one-dimensional irrep of Z

with parity eigenvalue c

and let B ∈ρ(V

), where ρ is a representation operator. Then a little thought shows

that the selection rule implies

|Bv

) =0 unless c

Thus if is B is parity-odd (c

=−1) then it can only connect states of opposite parity,

and if it is parity-even (c

=+1) then it can only connect states of the same parity.

If we were looking at dipolar radiative transitions (which emit a photon) between

electronic states of an atom or molecule, the relevant operators are the components

of the dipole operator p which is parity-odd (since it is a vector operator). The above

then tells us that dipolar radiative transitions can only occur between electronic

states of opposite parity.

Example 6.3 Angular momentum selection rules

Let (, H) be a complex unitary representation of SU(2), with two subspaces W

and W

equivalent to V

and V

, respectively, 2l,2j ∈ Z. Also suppose we have

an SU(2) representation operator A :V

→L(H), q ∈ Z. Then for any v ∈ W



∈W

, A ∈A(V

), the selection rule tells us that





|Av



=0 unless |l −q|≤j ≤l +q.

If we again consider a dipolar radiative transition between electronic states of an

atom or molecule, the relevant operator is still the dipole p whose components p

live in ρ(V

), and so we ﬁnd that a dipolar radiative transition between states with

angular momentum j and l can only occur if l −1 ≤j ≤l +1. 

The famous Wigner–Eckart theorem can be seen as a kind of complement to the

angular momentum selection rule above. In the notation of the previous example,

the Wigner–Eckart theorem says (roughly) that when (v



,Av)is not equal to zero, it

is still tightly constrained and is in fact determined up to a constant by the fact that

A is a representation operator. The precise statement is as follows:

Proposition 6.3 (Wigner–Eckart) Let (, H) be a complex unitary representation

of SU(2), with two subspaces W

and W

equivalent to V

and V

, respectively,

2l,2j ∈Z. Also suppose we have two SU(2) representation operators A, B :V

→

L(H), q ∈Z, which yield two spherical tensors with components A

≡A(v

), B

≡

B(v

),0≤k ≤2q +1. Finally, assume that







=0 for some k and v ∈W



∈W

. (6.11)

220 6 The Wigner–Eckart Theorem and Other Applications

Then for all k and w ∈W



∈W

, we have













(6.12)

for some constant c ∈C which is independent of k, w and w



Proof Let L(W

) denote the vector space of all linear maps from W

to W

.By

restricting to W

and using the orthogonal projection operator P

:H→W

, we can

turn A :V

→L(H) into a map

A :V

→L(W

)

v →P

◦A(v)|

All we have done here is take the linear operator A(v) ∈ L(H) and restrict it to

and then project onto W

. Now, since W

are SU(2)-invariant subspaces,

the vector space L(W

) actually furnishes a representation (



, L(W

)) of

SU(2) by



(g)T ≡(g)T (g)

−1

,T∈L(W

), g ∈SU(2). (6.13)

You will check below that this is a bona ﬁde representation, and is in fact equivalent

to the tensor product representation W

∗

⊗W

W

⊗W

! Furthermore, since the

action of SU(2) on H commutes with restriction and projection (cf. Problem 6.2), it

is not hard to see that

A is an intertwiner. From (6.11) we know that

A is not zero,

and so from Schur’s lemma we conclude that L(W

) W

⊗W

has a subspace

equivalent to V

, and that

A is a vector space isomorphism from V

to U

Now, we could also use our second representation operator B to construct a sec-

ond intertwiner

B : V

→ U

⊂ L(W

). Then we may invoke the corollary of

Schur’s lemma that you proved in Exercise 5.33 to conclude that

B =c

A. But this

then means that

A(v

) =c

B(v

) ∀k

⇒





A(v







B(v



∀k and w ∈W



∈W

⇒













∀k and w ∈W



∈W

and so we are done. In deducing the last line we used the deﬁnition of

A, the def-

inition of the orthogonal projection operator P

, and the deﬁnitions A

= A(v

=B(v

). 

Exercise 6.2 Show that if T ∈ L(W

) then so is (g)T (g)

−1

,sothat

(



, L(W

)) really is a representation; in fact, it is an invariant subspace of (

, L(H)).

In analogy to the equivalence between V

∗

⊗ V and L(V ), show that (



, L(W

)) is

equivalent to W

∗

⊗W

, which by Problem 5.3 is equivalent to W

⊗W

You may have noticed that this is not the way the Wigner–Eckart theorem is usu-

ally stated in advanced quantum mechanics texts like Sakurai [14]. There, the theo-

rem usually states that the matrix elements of a spherical tensor are proportional to

the Clebsch–Gordan coefﬁcients. To make this connection, consider the intertwiner

6.2 Selection Rules and the Wigner–Eckart Theorem 221

T :V

⊗W

→W

v ⊗w →P



A(v)w



If we work with standard bases {v

}

m=0−2q

, {w

}

n=0−2l

, {w



}

p=0−2j

for V

and W

, then this map has components



p



p



A(v



w









)



w











. (6.14)

Now let us switch to the orthonormal bases familiar from quantum mechanics,

which look like

|q,m

∈V

−q ≤m

≤q

|l,m

∈W

−l ≤m

≤l

|j,m





∈W

−j ≤m

≤j

(notice the prime on the last set of vectors, which will distinguish it from vectors

in V

⊗ W

with the same quantum numbers). With this basis and notation, the

components (6.14)ofT become the matrix elements



j,m

|l,m

.

What do these matrix elements have to do with Clebsch–Gordan coefﬁcients?

Recall that V

⊗W

has two convenient sets of orthonormal basis vectors:

|q,m

⊗|l,m

≡|ql;m

∈V

⊗W

, −q ≤m

≤q, −l ≤m

≤l



∈V

⊗W

, |l −q|≤l



≤l +q, −l



≤m



≤l



The Clebsch–Gordan coefﬁcients are just the inner products l



|ql;k,m

 of

these basis vectors. Since T : V

⊗W

→ W

is nonzero, V

⊗W

must contain a

subspace U

equivalent to W

, and so we can consider the orthogonal projection

operator P :V

⊗W

→U

. By Problem 6.1 this is given by

P :V

⊗W

→U

|ql;m

→



−j≤m

≤j

j,m

|ql;m

|j,m



and is an intertwiner by Problem 6.2. By then making the obvious identiﬁcation of

with W

and hence |j,m

→|j,m





, we get the intertwiner



⊗W

→W

|ql;m

→



−j≤m

≤j

j,m

|ql;m

|j,m





whose components are nothing but the Clebsch–Gordan coefﬁcients! By Wigner–

Eckart, though, this intertwiner must be proportional to T , and so its components

222 6 The Wigner–Eckart Theorem and Other Applications

must be proportional to those of T . We thus have the following component version

of the Wigner–Eckart theorem:

Proposition 6.4 (Wigner–Eckart II) Let (, H) be a complex unitary representa-

tion of SU(2), with two subspaces W

and W

equivalent to V

and V

, respectively,

2l,2j ∈Z. Also suppose we have a degree q spherical tensor A ={A

}. Then

j,m

|l,m

=cj,m

|ql;m

 (6.15)

where c is a constant independent of m

, m

, and m

6.3 Gamma Matrices and Dirac Bilinears

We conclude this short chapter with what is essentially an extended example, which

involves both the representation operators we have met in this chapter as well as

the O(3, 1) representation theory we developed in the last. This section relies on a

familiarity with the theory of the Dirac electron; if you have not seen this material,

and in particular are unfamiliar with gamma matrices and Dirac bilinears, then this

section can be skipped.

Let (D ≡ ⊕

, C

) be the Dirac spinor representation of SL(2, C), so that

D :SL(2, C) →GL(4, C)

A →D(A) ≡



A 0

0 A

†−1



We claim that the gamma matrices γ

can be seen as the components of a represen-

tation operator γ :R

→L(C

) =M

(C), where R

is the Minkowski four-vector

representation of SL(2, C). To deﬁne γ , we need the following two identiﬁcations

of R

with H

(C), where X =(x,t)∈R

and σ ≡(σ

,σ

↔H

(C)

X ↔X

∗

≡x ·σ +tI (6.16)

X ↔X

∗

≡x ·σ −tI. (6.17)

Note that (6.16) is just the identiﬁcation we used in Examples 4.20 and 5.5 in deﬁn-

ing the four-vector representation of SL(2, C), and (6.17) is just a slight variation of

that. Now, using the well-known property of the sigma matrices that

+σ

=2δ

, (6.18)

you will verify below that

∗

=η(X,X)X

−1

∗

. (6.19)

Also, if ρ : SL(2, C) →SO(3, 1)

is the homomorphism from Example 4.20 which

deﬁnes the four-vector representation, then by the deﬁnition of ρ we have

6.3 Gamma Matrices and Dirac Bilinears 223



ρ(A)X



∗

=AX

∗

†

, (6.20)

which when combined with (6.19) yields



ρ(A)X



∗

†−1

∗

−1

(6.21)

as you will also show below. If we then deﬁne a map γ by

γ :R

→M

(C)

X →



0 X

∗



you can then use (6.20) and (6.21) to check that γ is a representation operator, i.e.

that



ρ(A)X



=D(A)γ(X)D(A)

−1

. (6.22)

If we deﬁne the gamma matrices as γ

≡γ(e

), then we ﬁnd that



0 σ



,i=1, 2, 3



0 I

−I 0



≡γ



−I 0

0 I



Up to a few minus signs that have to do with our choice of signature for the

Minkowski metric, as well as the fact that most texts write γ

instead of γ

,this

is the familiar chiral representation of the gamma matrices (the chiral representa-

tion is the one in which γ

is diagonal). If we let 

be the components of ρ(A),

we can take X =e

in (6.22) to get



=D(A)γ

D(A)

−1

(6.23)

which is how (6.22) usually appears in physics texts. Another important property is

that the gamma matrices satisfy the fundamental anticommutation relation

+γ

=2η

μν

(6.24)

which you can easily verify.

Exercise 6.3 Verify (6.19), (6.21), (6.22), and (6.24).

Now we would like to construct the Dirac bilinears. Denote an element of C

ψ =





where ψ

and ψ

are two-component spinors living in (

, 0) and (0,

), respec-

tively. Also deﬁne the row vector

ψ by

ψ ≡



∗

,ψ

∗

