Jeanblanc M., Yor M., Chesney M. Mathematical Methods for Financial Markets
Подождите немного. Документ загружается.

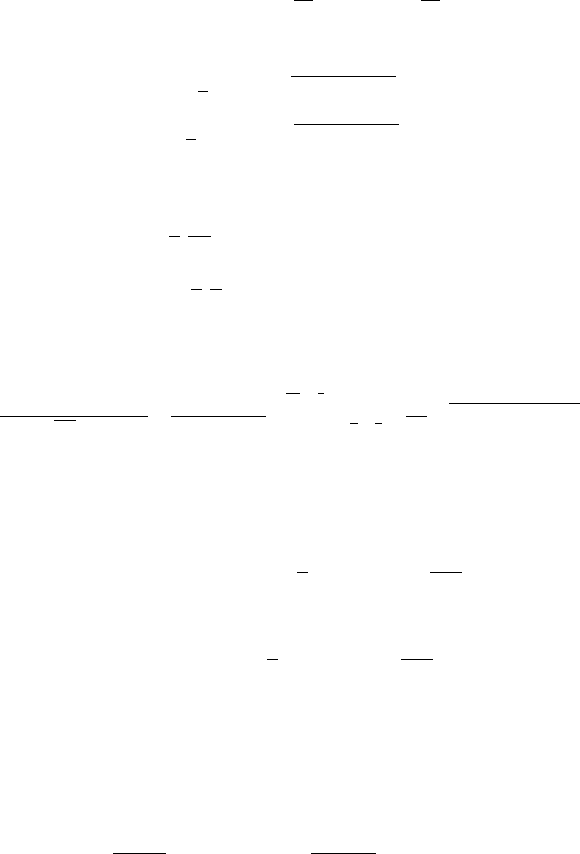
640 11 L´evy Processes
X
t
= G(t; ν
−1
,ν
1
) − G(t; ν
−1
,ν
2
) ,
where ν
i
,i =1, 2 are given below. Indeed, the characteristic function can be
factorized:
E(exp(iuX
t
)) =
1 −
iu
ν
1
−t/ν
1+
iu
ν
2
−t/ν
with
ν
−1
1
=
1
2
θν +
θ
2
ν
2
+2νσ
2
> 0 ,
ν
−1
2
=
1
2
−θν +
θ
2
ν
2
+2νσ
2
> 0 .
The L´evy density of the process X is
1
ν
1
|x|
exp(−ν
2
|x|), for x<0 ,
1
ν
1
x
exp(−ν
1
x), for x>0 .
The Variance-Gamma process has infinite activity. The density of the r.v. X
1
is
2e
θx/σ
2
ν
1/ν
√
2πσΓ(1/2)
x
2
θ
2
+2σ
2
/ν
1
2ν
−
1
4
K
1
ν
−
1
2
1
σ
2
x
2
(θ
2
+2σ
2
/ν)
where K
α
is the modified Bessel function.
In the risk-neutral world, stock prices driven by a Variance-Gamma process
have dynamics
S
t
= S
0
exp
rt + X
t
+
t
ν
ln
1 − θν −
σ
2
ν
2
.
Indeed, from
E(e
X
t
) = exp
−
t
ν
ln
1 − θν −
σ
2
ν
2
,
we get that the process (S
t
e
−rt
,t≥ 0) is a martingale. The parameters ν and
θ give control on skewness and kurtosis.
The tempered stable process is a L´evy process without Gaussian
component and with L´evy density
C
+
x
1+Y
+
e
−xM
+
1
{x>0}
+
C
−
|x|
1+Y
−
e
xM
−
1
{x<0}
where C
±
> 0,M
±
≥ 0, and Y
±
< 2. It was introduced by Koponen [537]and
used by Bouchaud and Potters [112] for financial modelling.

11.9 Valuation of Contingent Claims 641
The CGMY model, introduced by Carr et al. [150] is a particular case
of the tempered stable process (i.e., the case where C
+
= C
−
= C and
Y
+
= Y
−
= Y ). The L´evy density is
C
x
Y +1
e
−Mx
1
{x>0}
+
C
|x|
Y +1
e
Gx
1
{x<0}
with C>0,M ≥ 0,G≥ 0andY<2.
If Y<0, there is a finite number of jumps in any finite interval; if not, the
process has infinite activity. If Y ∈ [1, 2[, the process has infinite variation.
This process is also called KoBol (see Schoutens [766]).
11.9 Valuation of Contingent Claims
11.9.1 Perpetual American Options
In this section, we present the model derived in Chesney and Jeanblanc [174].
Suppose that the dynamics of the risky asset (a currency or a paying dividend
asset) are
S
t
= S
0
e
X
t
(11.9.1)
under the chosen risk-neutral probability Q where X is a L´evy process with
parameters (m, σ
2
,ν). We assume that E(e
λX
1
) < ∞ for every λ ∈ R. As seen
in Subsection 11.7.3, one has
− (r −δ)+m +
1
2
σ
2
+
(e
x
− 1 − x1
|x|≤1
)ν(dx)=0. (11.9.2)
By definition, the value of a perpetual American call with strike K is
C
A
(S
0
)=sup
τ∈T
E((S
τ
− K)e
−rτ
)whereT is the set of stopping times.
Mordecki [659] has proved that one can reduce attention to first hitting times,
i.e., to stopping times τ of the form
T (L)=inf{t ≥ 0:S
t
≥ L},
where L is a fixed boundary, with L ≥ S
0
. Therefore,
C
A
(S
0
)=sup
L
E
(S
T (L)
− K)e
−rT(L)
.
Let us define f as
f(x, L)=E
e
−rT(L)
(x exp(X
T (L)
) − K)
.
Then, the value of the American call is
C
A
(x)=sup
L≥x
f(x, L) .

642 11 L´evy Processes
Let =ln(L/x), T
X
()=inf{t ≥ 0,X
t
≥ } the hitting time of for the
process X,andO
the overshoot defined in terms of X by X
T ()
= + O
.
(Obviously, T
X
()=T
S
(L):=T
.) We introduce the function
g(x, )=f(x, L)=f (x, xe
)=xE(e
−rT
+X
T
) − KE(e
−rT
)
= xe
E(e
−rT
+0
) − KE(e
−rT
) .
Then, C
A
(x)=sup
≥0
g(x, ) .
General Formula
On the one hand, we define
ϕ(q, x)=xα(q,r) − Kβ(q,r)
with
α(q, r)=
+∞
0
e
−q
E(e
−rT
+O
)d , (11.9.3)
β(q, r)=
+∞
0
e
−q
E(e
−rT
)d . (11.9.4)
It is then not difficult to check that
ϕ(q, x)=
∞
0
e
−q
¯g(x, )d
where
¯g(x, )=g(xe
−
,)=xE(e
−rT
+O
) − KE(e
−rT
)=f(xe
−
,x) .
Thus
ϕ(q, x)=
∞
0
e
−q
¯g(x, )d =
x
0
e
−q ln(x/y)
¯g(x, ln(x/y))
1
y
dy
=
x
0
1
y
f(y, x)e
−q ln(x/y)
dy . (11.9.5)
On the other hand, as in Gerber and Landry [386], by definition of the
perpetual call exercise boundary b
c
:
for x<b
c
,f(x, b
c
)=sup
L≥x
f(x, L)
hence, assuming that f is differentiable,
∂f
∂L
(x, b
c
)=0,x<b
c
. (11.9.6)

11.9 Valuation of Contingent Claims 643
Therefore, by differentiation of (11.9.5) with respect to x at point b
c
∂ϕ
∂x
(q, b
c
)=
f(b
c
,b
c
)
b
c
−
q
b
c
ϕ(q, b
c
)
hence
α(q, r)=
b
c
− K
b
c
−
q
b
c
(b
c
α(q, r) − Kβ(q,r)) .
Now, due to the Pecherski-Rogozin identity (see Subsection 11.4.2), the
functions α and β are known in terms of the ladder exponent κ:
α(q, r)=
κ(r, q) − κ(r, −1)
(q +1)κ(r, q)
,β(q, r)=
κ(r, q) − κ(r, 0)
qκ(r, q)
(11.9.7)
and an easy computation leads to
b
c
=
κ(r, 0)
κ(r, −1)
K. (11.9.8)
Proposition 11.9.1.1 The boundary of a perpetual American call is given
by
b
c
=
κ(r, 0)
κ(r, −1)
K
where κ is the ladder exponent of X.
Comment 11.9.1.2 If E(e
X
1
) < ∞, using the Wiener-Hopf factorization,
Mordecki [659] proves that the boundaries for perpetual American options
are given by
b
p
= KE(e
m
Θ
),b
c
= KE(e
Σ
Θ
)
where m
t
=inf
s≤t
X
s
and Θ is an exponential r.v. independent of X with
parameter r, hence b
c
b
p
=
rK
2
1 − ln E(e
X
1
)
. This last equality follows from
E(e
ium
Θ
)E(e
iuΣ
Θ
)=
κ(r, 0)κ(r, 0)
κ(r, −iu)κ(r, iu)
=
r
r + Φ(u)
with Φ(u)=−ln E(e
iuX
1
). The equality between E(e
Σ
θ
)and
κ(r,0)
κ(r,−1)
is
obtained in Nguyen-Ngoc and Yor [671] using Wiener-Hopf decomposition.
A Particular Case: X without Positive Jumps
If the process X has no positive jumps, then, we obtain the well-known result
derived e.g. in Zhang [874] (see Subsection 10.7.2). Indeed, in that case, if Ψ
is the Laplace exponent of X,
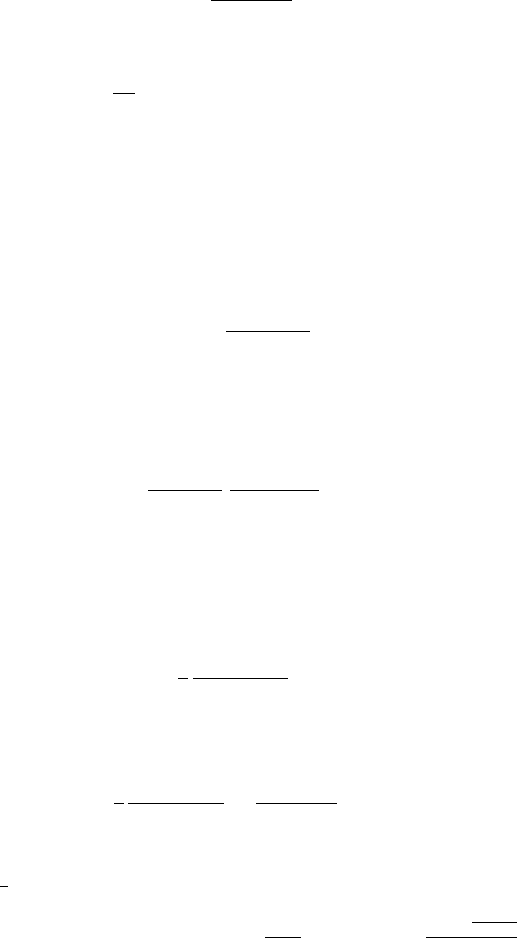
644 11 L´evy Processes
κ(α, β)=Ψ
(α)+β
where Ψ
(z)isthepositivenumbery such that Ψ (y)=z. Hence
b
c
= K
Ψ
(r)
Ψ
(r) − 1
.
Note that
Ψ(λ)=λm + λ
2
σ
2
2
+
(e
λx
− 1 − λx1
|x|≤1
)ν(dx) . (11.9.9)
The function Ψ is convex, Ψ(0) = 0 and Ψ(1) = r − δ. (This last property is
a consequence of the martingale criterion (11.9.2).)
A Second Particular Case: X without Negative Jumps
We now assume that the jumps of X are positive hence the dual process
X = −X has no positive jumps. Then
κ(u, k)=
u −
Ψ(k)
Ψ
(u) − k
(11.9.10)
where
Ψ is the L´evy exponent of −X, given by
Ψ(k)=Ψ (−k)and
Ψ
(z)is
the positive root of
Ψ(y)=z. Relying on equations (11.9.8)and(11.9.10), the
exercise boundary is given by:
b
c
=
r −
Ψ(0)
Ψ
(r)
Ψ
(r)+1
r −
Ψ(−1)
K.
Using that
Ψ(0) = 0,
Ψ(−1) = Ψ(1) = r − δ,and
Ψ
(r)=−Ψ
,n
(r), where
Ψ
,n
(r) is the negative root of Ψ(k)=r, we obtain the following proposition:
Proposition 11.9.1.3 The exercise boundary for a perpetual call written on
the exponential of a L´evy process without negative jumps is
b
c
=
r
δ
Ψ
,n
(r) − 1
Ψ
,n
(r)
K. (11.9.11)
Comment 11.9.1.4 It is straightforward to check that in the case ν =0,
the formula coincides with the usual formula (3.11.12). Indeed, in this case,
r
δ
Ψ
,n
0
(r) − 1
Ψ
,n
0
(r)
=
Ψ
0
(r)
Ψ
0
(r) − 1
(11.9.12)
where Ψ
0
is the L´evy exponent in the case φ =0,sothatΨ
0
(r)isthepositive
root of bk +
1
2
σ
2
k(k −1) = r and Ψ
,n
0
(r) is the negative root. Usual relations
between the sum and the product of roots and the coefficients for a second
order polynomial, lead to the result, b
c
=
γ
1
γ
1
−1
K with γ
1
=
−ν+
√
ν
2
+2r
σ
(see
(3.11.10)).
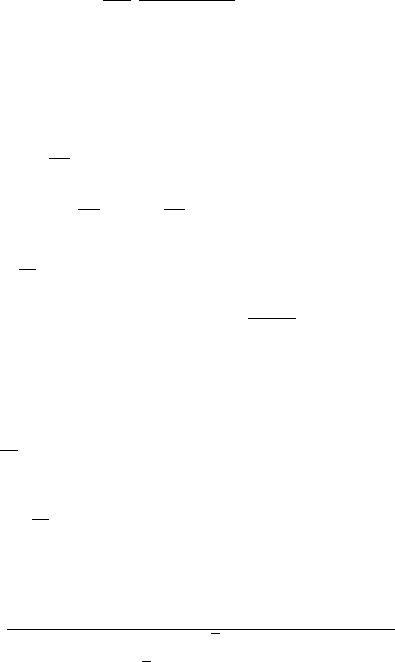
11.9 Valuation of Contingent Claims 645
The Perpetual American Currency Put
The put case can be solved by using the symmetrical relationship (see Fajardo
and Mordecki [339]) between the American call and put boundaries:
b
p
(K, r, δ, Ψ)b
c
(K, δ, r,
Ψ)=K
2
where
Ψ(u)=Ψ(1 − u) − Ψ (1) . (11.9.13)
And by relying on (11.9.11), the exercise boundary b
p
of the perpetual put in
a jump-diffusion setting with negative jumps can be obtained:
b
p
=
rK
δ
Ψ
,n
(δ)
Ψ
,n
(δ) − 1
. (11.9.14)
ThecasewherethesizeofthejumpsofX is a strictly positive constant
ϕ corresponds to ν(dx)=λδ
ϕ
(dx), with λ>0. Set φ = e
ϕ
− 1. In that case,
the Laplace exponent of the L´evy process X is
Ψ(u)=uμ + u
2
σ
2
2
+ λ(e
uϕ
− 1)
= u
r − δ −
σ
2
2
+ u
2
σ
2
2
+ λ((1 + φ)
u
− 1 − uφ)
with μ = r − δ − λφ −
σ
2
2
. Recall that in the case of jumps of constant size
b
p
(K, r, δ, λ, ϕ)b
c
(K, δ, r, λ(1 + ϕ), −
ϕ
1+ϕ
)=K
2
.
The price of a perpetual American call option can be decomposed as
C
A
(x)=δx
+∞
n=0
1
n!
+∞
0
e
−(δ+λ(1+φ))s
(λ(1 + φ)s)
n
N(d
1
(b
c
,n; s))ds
− rK
+∞
n=0
1
n!
+∞
0
e
−(r+λ)s
(λs)
n
N(d
2
(b
c
,n; s))ds (11.9.15)
with
d
1
(z,n; s)=
ln(x/z)+(r − δ − λφ + σ
2
/2)s + n ln(1 + φ)
σ
√
s
,
d
2
(z,n; s)=d
1
(z,n; s) − σ
√
s.
Comment 11.9.1.5 The perpetual exercise boundary for the put can also be
obtained by relying on the procedure used for the call. It can also be checked
that, when there is no dividend and when the L´evy measure corresponds to a
646 11 L´evy Processes
compound Poisson process, this formula is the same as in Gerber and Landry
[386], i.e.,
b
c
= rK
m + σ
2
+
(xe
x
− x1
|x|≤1
)ν(dx)
−1
.
See Chesney and Jeanblanc [174] for details.
Comment 11.9.1.6 The problem of American options is studied in Alili
and Kyprianou [8], Asmussen et al. [24], Boyarchenko and Levendorskii [117],
Chan [160, 159], Kyprianou and Pistorius [555] and Mordecki [658]. Russian
options are presented in Avram et al. [32], Asmussen et al. [24]andMordecki
and Moreira [660]. Barrier and lookback options are studied in Avram et al.
[31] and Nguyen-Ngoc and Yor [670, 671].
Il faut imaginer Sisyphe heureux.
A. Camus, Le Mythe de Sisyphe

A
List of Special Features, Probability Laws,
and Functions
A.1 Main Formulae
For the reader’s convenience, we give here a list of some main formulae and
the page numbers where they appeared. They are presented, for each topic,
in alphabetical order. We have not given details of notation, which should be
clear from the context.
A.1.1 Absolute Continuity Relationships
Cameron-Martin’s Formula. (Page 73)
W
(ν)
[F (X
t
,t≤ T )] = W
(0)
[e
νX
T
−ν
2
T/2
F (X
t
,t≤ T )]
Girsanov’s Theorem. (Page 73)
W
(f)
[F (X
t
,t≤ T )]
= W
(0)
exp
T
0
f(X
s
)dX
s
−
1
2
T
0
f
2
(X
s
)ds
F (X
t
,t≤ T )
Squared Radial Ornstein-Uhlenbeck Processes and Squared Bessel
Processes. (Page 356)
b
Q
a
x
|
F
t
=exp
−
b
4
(X
t
− x − at) −
b
2
8
t
0
X
s
ds
Q
a
x
|
F
t
M. Jeanblanc, M. Yor, M. Chesney, Mathematical Methods for Financial
Markets, Springer Finance, DOI 10.1007/978-1-84628-737-4,
c
Springer-Verlag London Limited 2009
647
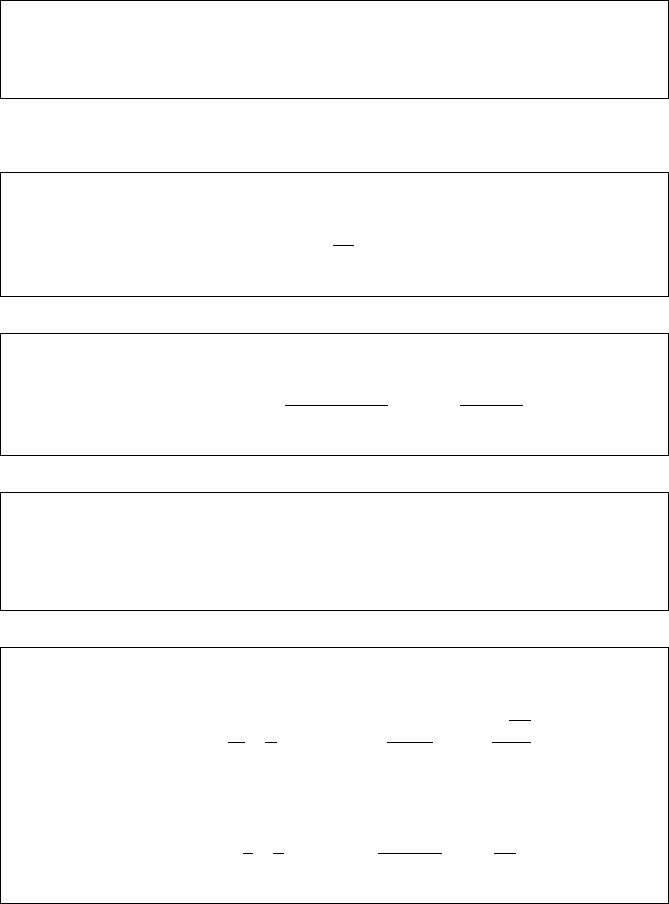
648 A List of Special Features, Probability Laws, and Functions
Poisson Processes of Intensities λ and (1 + β)λ. (Page 466)
Π
(1+β)λ
|
F
t
=
(1 + β)
N
t
e
−λβt
Π
λ
|
F
t
A.1.2 Bessel Processes
The CIR Process r is a space-time changed BESQ process ρ. (Page 357)
r
t
= e
−kt
ρ
σ
2
4k
(e
kt
− 1)
Laplace Transform for the BESQ. (Page 343)
Q
δ
x
[exp(−λρ
t
)] =
1
(1 + 2λt)
δ/2
exp
−
λx
1+2λt
Scale Functions.
For a squared Bessel process (Page 336)
−x
1−(δ/2)
for δ>2; ln x for δ =2; x
1−(δ/2)
for δ<2
Transition Densities. (Page 343)
For a squared Bessel process of index ν
q
(ν)
t
(x, y)=
1
2t
y
x
ν/2
exp
−
x + y
2t
I
ν
√
xy
t
ForaBesselprocessofindexν
p
(ν)
t
(x, y)=
y
t
y
x
ν
exp
−
x
2
+ y
2
2t
I
ν
xy
t
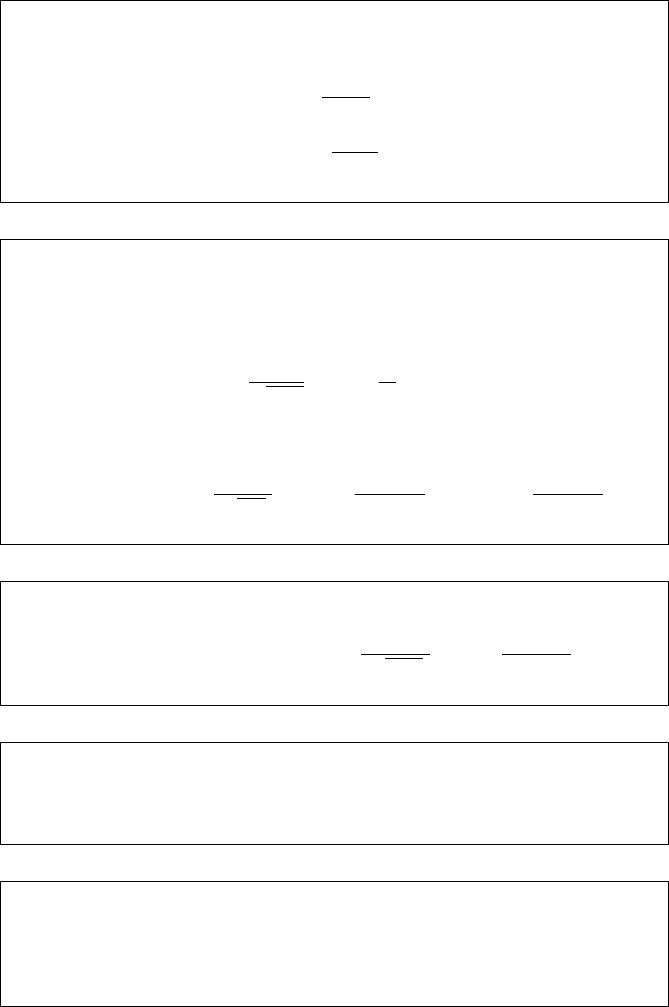
A.1 Main Formulae 649
A.1.3 Brownian Motion
Let W be a Brownian motion, and M
t
=sup
s≤t
W
s
.
Brownian Bridges.
The following processes are Brownian bridges on [0,T] (Page 237)
X
t
=(T −t)
t
0
dW
s
T − s
;0≤ t ≤ T
Y
t
=(T −t) W
t
T − t
, 0 ≤ t ≤ T
Hitting Times.
Law of the hitting time of y>0foradriftedBM:X
t
= W
t
+ νt, ν>0
(Page 148)
P(T
y
(X) ∈ dt)=
y
√
2πt
3
exp
−
1
2t
(y − νt)
2
1
{t≥0}
dt
Joint law of W
t
and first hitting time of 0. (Page 142)
P
z
(W
t
∈ dx, T
0
≥ t)=
1
{x≥0}
√
2πt
exp
−
(z − x)
2
2t
− exp
−
(z + x)
2
2t
dx
Joint Law of B and its Local Time. (Page 222)
P(|B
t
|∈dx, L
0
t
∈ d)=1
{x≥0}
1
{≥0}
2(x + )
√
2πt
3
exp
−
(x + )
2
2t
dx d
L´evy’s Equivalence Theorem. (Page 218)
(|W
t
|,L
t
; t ≥ 0)
law
=(M
t
− W
t
,M
t
; t ≥ 0)
Occupation Time Formula. (Page 212)
t
0
f(W
s
) ds =
+∞
−∞
L
x
t
f(x) dx
