Jeanblanc M., Yor M., Chesney M. Mathematical Methods for Financial Markets
Подождите немного. Документ загружается.

450 7 Default Risk: An Enlargement of Filtration Approach
From Girsanov’s theorem (see Section 9.4), the processes
"
W and
"
M,
given by
"
W
t
= W
t
−
t
0
θ
u
du,
"
M
t
= M
t
−
t
0
1
{u<τ}
λ
u
ζ
u
du, (7.9.3)
are G-martingales under Q
1
. To ensure that Y
2,1
is a Q
1
-martingale, we have
to choose
θ
t
=
r
t
− μ
2,t
σ
2,t
.
For the process Y
3,1
to be a Q
1
-martingale, it is necessary and sufficient that
ζ satisfies
λ
t
ζ
t
= μ
3,t
− r
t
+ σ
3,t
r
t
− μ
2,t
σ
2,t
.
To ensure that Q
1
is a probability measure equivalent to P,werequirethat
ζ
t
> −1. The unique martingale measure Q
1
is then given by
L
t
= E
t
·
0
θ
u
dW
u
E
t
·
0
ζ
u
dM
u
.
Proposition 7.9.1.1 Assume that the process θ
t
=
r
t
−μ
2,t
σ
2,t
is bounded, and
ζ
t
=
1
λ
t
μ
3,t
− r
t
+ σ
3,t
r
t
− μ
2,t
σ
2,t
> −1. (7.9.4)
Then the market is arbitrage free and complete. The dynamics of the relative
prices under the unique martingale measure Q
1
are
dY
2,1
t
= Y
2,1
t
σ
2,t
d
"
W
t
,
dY
3,1
t
= Y
3,1
t−
σ
3,t
d
"
W
t
− d
"
M
t
.
This means that any Q
1
-integrable contingent claim Y = G(Y
2
T
,Y
3
T
; D
T
)
is attainable, and its arbitrage price equals
π
t
(Y )=R
−1
t
E(YR
T
|G
t
), ∀t ∈ [0,T] (7.9.5)
where R
t
=exp(−
t
0
r
s
ds).
7.9.2 PDE for Valuation
Since our goal is to develop the PDE approach, it will be essential to postulate
the Markovian property of our model. We assume that the coefficients μ
i
,σ
i
,λ
are regular functions of (t, Y
2
t
,Y
3
t
−
).
Lemma 7.9.2.1 The process (Y
1
,Y
2
,Y
3
,D) is a G-Markov process under
the martingale measure Q
1
. For any attainable claim Y = G(Y
1
T
,Y
2
T
,Y
3
T
; D
T
)
there exists a function C :[0,T] × R
3
×{0, 1}→R such that
π
t
(Y )=C(t, Y
1
t
,Y
2
t
,Y
3
t
; D
t
) .
7.9 PDE Approach for Hedging Defaultable Claims 451
Note that, since Y
1
T
is deterministic, up to a change of notation one
can restrict attention to claims of the form G(Y
2
T
,Y
3
T
; D
T
), the price of
which is C(t, Y
2
t
,Y
3
t
; D
t
). We find it convenient to introduce the pre-default
pricing function C(·;0) = C(t, y
2
,y
3
;0) and the post-default pricing function
C(·;1) = C(t, y
2
,y
3
; 1). In fact, since Y
3
t
=0ifD
t
= 1, it suffices to study
the post-default function C(t, y
2
;1)=C(t, y
2
, 0; 1). Also, we write
b =(r − μ
3
)σ
3
− (μ
3
− r)σ
2
.
Let λ>0 be the default intensity under P,andletζ>−1 be given by formula
(7.9.4) where we do not indicate the dependence on t. (In fact, b, σ, λ and ζ
are Markovian coefficients.) We denote by ∂
i
,i =1, 2 the partial derivative
with respect to y
i
.
Proposition 7.9.2.2 Assume that the functions C(·;0) and C(·;1) belong
to the class C
1,2
([0,T] × R
+
× R
+
, R).ThenC(t, y
2
,y
3
;0) satisfies the PDE
∂
t
C(·;0) + ry
2
∂
2
C(·;0)+(r + ζ)y
3
∂
3
C(·;0)+
1
2
3
i,j=2
σ
i
σ
j
y
i
y
j
∂
ij
C(·;0)
− rC(·;0)+
λ +
b
σ
2
C(t, y
2
;1)− C(t, y
2
,y
3
;0)
=0
subject to the terminal condition C(T,y
2
,y
3
;0) = G(y
2
,y
3
;0),andC(t, y
2
;1)
satisfies the PDE
∂
t
C(·;1)+ry
2
∂
2
C(·;1)+
1
2
σ
2
2
y
2
2
∂
22
C(·;1)− rC(·;1) = 0
subject to the terminal condition C(T,y
2
;1)=G(y
2
, 0; 1).
Proof: For simplicity, we write C
t
= π
t
(Y ). Let us define
ΔC(t, y
2
,y
3
)=C(t, y
2
;1)− C(t, y
2
,y
3
;0).
Then the jump ΔC
t
= C
t
− C
t−
can be represented as follows:
ΔC
t
= 1
{τ=t}
C(t, Y
2
t
;1)− C(t, Y
2
t
,Y
3
t
−
;0)
= 1
{τ=t}
ΔC(t, Y
2
t
,Y
3
t
−
).
We typically omit the variables (t, Y
2
t
−
,Y
3
t
−
,D
t
−
) in expressions ∂
t
C, ∂
i
C, ΔC,
etc. We shall also make use of the fact that for any Borel measurable function
g we have
t
0
g(u, Y
2
u
,Y
3
u
−
) du =
t
0
g(u, Y
2
u
,Y
3
u
) du
since Y
3
u
and Y
3
u
−
differ for at most one value of u (for each ω).
Let ξ
t
= 1
{t<τ}
λ
t
. An application of Itˆo’s formula yields
452 7 Default Risk: An Enlargement of Filtration Approach
dC
t
= ∂
t
Cdt+
3
i=2
∂
i
CdY
i
t
+
1
2
3
i,j=2
σ
i
σ
j
Y
i
t
Y
j
t
∂
ij
Cdt
+
ΔC + Y
3
t
−
∂
3
C
dD
t
= ∂
t
Cdt+
3
i=2
∂
i
CdY
i
t
+
1
2
3
i,j=2
σ
i
σ
j
Y
i
t
Y
j
t
∂
ij
Cdt
+
ΔC + Y
3
t
−
∂
3
C
dM
t
+ ξ
t
dt
,
and this in turn implies that
dC
t
= ∂
t
Cdt+
3
i=2
Y
i
t
∂
i
C
μ
i
dt + σ
i
dW
t
+
1
2
3
i,j=2
σ
i
σ
j
Y
i
t
Y
j
t
∂
ij
Cdt
+ ΔC dM
t
+
ΔC + Y
3
t
−
∂
3
C
ξ
t
dt
=
⎛
⎝
3
i=2
μ
i
Y
i
t
∂
i
C +
1
2
3
i,j=2
σ
i
σ
j
Y
i
t
Y
j
t
∂
ij
C +
ΔC + Y
3
t
∂
3
C
ξ
t
⎫
⎬
⎭
dt
+ ∂
t
C +
3
i=2
σ
i
Y
i
t
∂
i
C
dW
t
+ ΔC dM
t
.
We now use the integration by parts formula to derive dynamics of the relative
price
C
t
= C
t
(Y
1
t
)
−1
. We find that
Y
1
t
d
C
t
=
3
i=2
σ
i
Y
i
t
∂
i
CdW
t
+ ΔC dM
t
+(∂
t
C − rC
t
) dt
+
⎧
⎨
⎩
3
i=2
μ
i
Y
i
t
∂
i
C +
1
2
3
i,j=2
σ
i
σ
j
Y
i
t
Y
j
t
∂
ij
C +
ΔC + Y
3
t
∂
3
C
ξ
t
⎫
⎬
⎭
dt .
Hence, using (7.9.3), we obtain
Y
1
t
d
C
t
=
3
i=2
σ
i
Y
i
t
∂
i
Cd
"
W
t
+ ΔC d
"
M
t
− rC
t
dt + ∂
t
C
+
⎧
⎨
⎩
3
i=2
μ
i
Y
i
t
∂
i
C +
1
2
3
i,j=2
σ
i
σ
j
Y
i
t
Y
j
t
∂
ij
C +
ΔC + Y
3
t
∂
3
C
ξ
t
⎫
⎬
⎭
dt
+
3
i=2
σ
i
Y
i
t
θ∂
i
C + ζξ
t
ΔC − σ
1
3
i=2
σ
i
Y
i
t
∂
i
C
dt.
This means that the process
C admits the following decomposition under Q
1
7.9 PDE Approach for Hedging Defaultable Claims 453
Y
1
t
d
C
t
= −rC
t
dt +
3
i=2
σ
i
Y
i
t
θ∂
i
C + ζξ
t
ΔC + ∂
t
C
dt
+
⎛
⎝
3
i=2
μ
i
Y
i
t
∂
i
C +
1
2
3
i,j=2
σ
i
σ
j
Y
i
t
Y
j
t
∂
ij
C +
ΔC + Y
3
t
∂
3
C
ξ
t
⎞
⎠
dt
+ d(a Q
1
-martingale) .
From (7.9.5), it follows that the process
C is a martingale under Q
1
. Therefore,
the continuous finite variation part in the above decomposition necessarily
vanishes, and thus we get
0=−rC
t
+ ∂
t
C +
3
i=2
μ
i
Y
i
t
∂
i
C +
1
2
3
i,j=2
σ
i
σ
j
Y
i
t
Y
j
t
∂
ij
C
+
ΔC + Y
3
t
∂
3
C
ξ
t
+
3
i=2
σ
i
Y
i
t
θ∂
i
C + ζξ
t
ΔC .
Finally, we conclude that
∂
t
C + rY
2
t
∂
2
C +(r + ξ
t
) Y
3
t
∂
3
C +
1
2
3
i,j=2
σ
i
σ
j
Y
i
t
Y
j
t
∂
ij
C
− rC
t
+(1+ζ)ξ
t
ΔC =0.
Recall that ξ
t
= 1
{t<τ}
λ. It is thus clear that the pricing functions C(·, 0) and
C(·; 1) satisfy the PDEs given in the statement of the proposition.
Hedging Strategy
The next result provides a replicating strategy for Y .
Proposition 7.9.2.3 The replicating strategy φ for the claim Y is given by
the formulae
φ
3
t
Y
3
t−
= −ΔC(t, Y
2
t
,Y
3
t−
)=C(t, Y
2
t
,Y
3
t−
;0)− C(t, Y
2
t
;1),
φ
2
t
σ
2
Y
2
t
= σ
3
ΔC +
3
i=2
Y
i
t
σ
i
∂
i
C,
φ
1
t
Y
1
t
= C −φ
2
t
Y
2
t
− φ
3
t
Y
3
t
.
Proof: As a by-product of our previous computations, we obtain
d
C
t
=(Y
1
t
)
−1
3
i=2
σ
i
Y
i
t−
∂
i
Cd
"
W
t
+(Y
1
t
−
)
−1
ΔC d
"
M
t
.

454 7 Default Risk: An Enlargement of Filtration Approach
The self-financing strategy that replicates Y is determined by two components
φ
2
,φ
3
and the following relationship:
d
C
t
= φ
2
t
dY
2,1
t
+ φ
3
t
dY
3,1
t
= φ
2
t
Y
2,1
t
σ
2
d
"
W
t
+ φ
3
t
Y
3,1
t−
σ
3
d
"
W
t
− d
"
M
t
.
By identification, we obtain φ
3
t
Y
3,1
t−
=(Y
1
t
)
−1
ΔC and
φ
2
t
σ
2
Y
2
t
− σ
3
ΔC =
3
i=2
Y
i
t
−
σ
i
∂
i
C.
This yields the claimed formulae.
Corollary 7.9.2.4 In the case of a total default claim, the hedging strategy
satisfies the condition φ
1
t
Y
1
t
+ φ
2
t
Y
2
t
=0.
Proof: A total default corresponds to the assumption that G(y
2
,y
3
, 1) = 0.
We then have C(t, y
2
; 1) = 0, and thus φ
3
t
Y
3
t−
= C(t, Y
1
t
,Y
2
t
,Y
3
t−
; 0) for every
t ∈ [0,T]. Hence, the equality φ
1
t
Y
1
t
+ φ
2
t
Y
2
t
= 0 holds for every t ∈ [0,T]
and ensures that the wealth of a replicating portfolio jumps to zero at default
time.
7.9.3 General Case
Proposition 7.9.3.1 Let σ
2
=0and let Y
1
,Y
2
,Y
3
satisfy
dY
1
t
= rY
1
t
dt,
dY
2
t
= Y
2
t
μ
2
dt + σ
2
dW
t
,
dY
3
t
= Y
3
t
−
μ
3
dt + σ
3
dW
t
+ κ
3
dM
t
.
Assume that κ
3
=0,κ
3
> −1. The market is complete and arbitrage free if
and only if σ
2
(r − μ
3
)=σ
3
(r − μ
2
).
Proof: We leave this to the reader.
Corollary 7.9.3.2 In case of constant coefficients, the risk-neutral intensity
is equal to the historical intensity.
Proof: This follows from the determination of the unique risk-neutral
probability, which transforms the Brownian motion W into
"
W where
d
"
W
t
= W
t
−
μ
2
− r
σ
2
dt = W
t
−
μ
3
− r
σ
3
dt ,
but does not change the martingale M.
7.9 PDE Approach for Hedging Defaultable Claims 455
Proposition 7.9.3.3 The price of a contingent claim Y = G(Y
2
T
,Y
3
T
,D
T
)
can be represented as π
t
(Y )=C(t, Y
2
t
,Y
3
t
,D
t
), where the pricing functions
C(·;0) and C(·;1) satisfy the following PDEs:
∂
t
C(t, y
2
,y
3
;0) + ry
2
∂
2
C(t, y
2
,y
3
;0)+y
3
(r − κ
3
λ) ∂
3
C(t, y
2
,y
3
;0)
+
1
2
3
i,j=2
σ
i
σ
j
y
i
y
j
∂
ij
C(t, y
2
,y
3
;0)
+ λ
C(t, y
2
,y
3
(1 + κ
3
); 1) − C(t, y
2
,y
3
;0)
= rC(t, y
2
,y
3
;0)
and
∂
t
C(t, y
2
,y
3
;1)+ry
2
∂
2
C(t, y
2
,y
3
;1)+ry
3
∂
3
C(t, y
2
,y
3
;1)− rC(t, y
2
,y
3
;1)
+
1
2
3
i,j=2
σ
i
σ
j
y
i
y
j
∂
ij
C(t, y
2
,y
3
;1)=0
subject to the terminal conditions
C(T,y
2
,y
3
;0)=G(y
2
,y
3
;0),C(T,y
2
,y
3
;1)=G(y
2
,y
3
;1).
The replicating strategy φ comprises
φ
2
t
=
1
σ
2
Y
2
t
3
i=2
σ
i
y
i
∂
i
C(t, Y
2
t
,Y
3
t−
,D
t−
)
−
σ
3
σ
2
κ
3
Y
2
t
C(t, Y
2
t
,Y
3
t−
(1 + κ
3
); 1) − C(t, Y
2
t
,Y
3
t−
;0)
,
φ
3
t
=
1
κ
3
Y
3
t−
C(t, Y
2
t
,Y
3
t−
(1 + κ
3
); 1) − C(t, Y
2
t
,Y
3
t−
;0)
,
with φ
1
t
given by φ
1
t
Y
1
t
+ φ
2
t
Y
2
t
+ φ
3
t
Y
3
t
= C
t
.
Proof: This is obtained by lengthy computations, as in Proposition 7.9.2.2.
We leave the details to the reader.
Hedging of a Survival Claim
We shall illustrate Proposition 7.9.3.3 by means of an example. Consider a
survival claim of the form
Y = G(Y
2
T
,Y
3
T
,D
T
)=1
{T<τ}
g(Y
3
T
).
Then the post-default pricing function C
g
(·; 1) vanishes identically, and the
pre-default pricing function C
g
(·; 0) solves the PDE

456 7 Default Risk: An Enlargement of Filtration Approach
∂
t
C
g
(·;0)+ry
2
∂
2
C
g
(·;0)+y
3
(r − κ
3
λ) ∂
3
C
g
(·;0)
+
1
2
3
i,j=2
σ
i
σ
j
y
i
y
j
∂
ij
C
g
(·;0)− (r + λ)C
g
(·;0)=0
with the terminal condition C
g
(T,y
2
,y
3
;0)=g(y
3
). Denote α = r − κ
3
λ and
β = λ(1 + κ
3
).
It is not difficult to check that C
g
(t, y
2
,y
3
;0) = e
β(T −t)
C
α,g,3
(t, y
3
)isa
solution of the above equation, where the function w(t, y)=C
α,g,3
(t, y)isthe
solution of the standard Black and Scholes PDE
∂
t
w + yα∂
y
w +
1
2
σ
2
3
y
2
∂
yy
w − αw =0
with the terminal condition w(T,y)=g(y), that is, the price of the contingent
claim g(Y
T
) in the Black and Scholes framework with interest rate α and
volatility parameter equal to σ
3
.
Let C
t
be the current value of the contingent claim Y ,sothat
C
t
= 1
{t<τ}
e
β(T −t)
C
α,g,3
(t, Y
3
t
).
The hedging strategy of the survival claim is, on the event {t<τ},
φ
3
t
Y
3
t
= −
1
κ
3
e
−β(T −t)
C
α,g,3
(t, Y
3
t
)=−
1
κ
3
C
t
,
φ
2
t
Y
2
t
=
σ
3
σ
2
Y
3
t
e
−β(T −t)
∂
y
C
α,g,3
(t, Y
3
t
) − φ
3
t
Y
3
t
.
Obviously, there is no need for the strategy on the set {τ<t}.

8
Poisson Processes and Ruin Theory
We give in this chapter the main results on Poisson processes, which are
basic examples of jump processes. Despite their elementary properties they
are building blocks of jump process theory. We present various generalizations
such as inhomogeneous Poisson processes and compound Poisson processes.
These processes are not used to model financial prices, due to the simple
character of their jumps and are in practice mixed with Brownian motion, as
we shall present in Chapter 10. However, they represent the main model in
insurance theory. We end this chapter with two sections about point processes
and marked point processes.
The reader can refer to C¸inlar [188], Cocozza-Thivent [190], Karlin and
Taylor [515] and the last chapter in Shreve [795] for the study of standard
Poisson processes, to Br´emaud [124] for general Poisson processes, and to
Jacod and Shiryaev [471], Kallenberg [504], Kingman [523], Last and Brandt
[565], Neveu [669], Prigent [725] and Protter [727] for point processes, and to
Mikosch [651, 652] for applications.
8.1 Counting Processes and Stochastic Integrals
A counting process is a process which increases in unit steps at isolated
times and is constant between these times. It can be constructed as follows. Let
(T
n
,n≥ 0) be a sequence of random variables defined on the same probability
space (Ω,F, P) such that
T
0
=0,T
n
<T
n+1
for T
n
< ∞.
This sequence models the times when jumps occur. We define the family of
random variables, for t ≥ 0,
N
t
=
n if t ∈ [T
n
,T
n+1
[
+∞ otherwise,
M. Jeanblanc, M. Yor, M. Chesney, Mathematical Methods for Financial
Markets, Springer Finance, DOI 10.1007/978-1-84628-737-4
8,
c
Springer-Verlag London Limited 2009
457
458 8 Poisson Processes and Ruin Theory
or, equivalently,
N
t
=
n≥1
1
{T
n
≤t}
=
n≥0
n1
{T
n
≤t<T
n+1
}
,N
0
=0.
This counting process (N
t
,t≥ 0), associated with the sequence (T
n
,n≥ 0), is
increasing and right-continuous. We denote by N
t
−
the left-limit of N
s
when
s → t,s<tand by ΔN
s
= N
s
−N
s−
the jump process of N.Theexplosion
time is the r.v. T =sup
n
T
n
. In what follows, we reduce our attention to the
case T = ∞.
Let F be a given filtration. A counting process is F-adapted if and only if
the random variables (T
n
,n ≥ 1) are F-stopping times. In that case, for any
n,theset{N
t
≤ n} = {T
n+1
>t} belongs to F
t
.
The natural filtration of N denoted by F
N
where F
N
t
= σ(N
s
,s ≤ t)is
the smallest filtration F
N
which satisfies the usual hypotheses and such that
N is F
N
-adapted.
The stochastic integral
t
0
C
s
dN
s
is defined pathwise as a Stieltjes
integral for every bounded measurable process (not necessarily F
N
-adapted)
(C
t
,t≥ 0) by
(CN)
t
:=
t
0
C
s
dN
s
=
]0,t]
C
s
dN
s
:=
∞
n=1
C
T
n
1
{T
n
≤t}
.
We emphasize that the integral
t
0
C
s
dN
s
is here an integral over the time
interval ]0,t], where the upper limit t is included and the lower limit 0
excluded. This integral is finite since there is a finite number of jumps during
thetimeinterval]0,t]. We shall also write
t
0
C
s
dN
s
=
s≤t
C
s
ΔN
s
where the right-hand side contains only a finite number of non-zero terms. The
integral
∞
0
C
s
dN
s
is defined as
∞
0
C
s
dN
s
=
∞
n=1
C
T
n
, when the right-hand
side converges.
We shall also use the differential notation d(CN)
t
:=C
t
dN
t
.
We can associate a random measure to any counting process as follows.
For any Borel set Λ ⊂ R
+
, for any ω,set
μ(ω, Λ)=#{n ≥ 1:T
n
(ω) ∈ Λ}.
For any ω,themapΛ → μ(ω, Λ) defines a positive measure on R
+
. One can
note that μ(ω, dt)=
n
δ
T
n
(ω)
(dt).
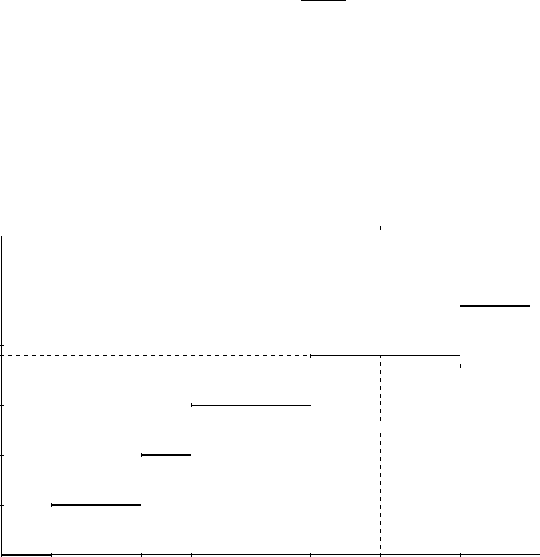
8.2 Standard Poisson Process 459
The random variable N
t
canbewrittenas
N
t
(ω)=μ(ω,]0,t]) =
]0,t]
μ(ω, ds)
and the Stieltjes (or stochastic) integral as
t
0
C
s
dN
s
=
t
0
C
s
μ(ds).
8.2 Standard Poisson Process
8.2.1 Definition and First Properties
The standard Poisson process is a counting process such that the random
variables (T
n+1
−T
n
,n≥ 0) are independent and identically distributed with
exponential law of parameter λ with λ>0. Hence, the explosion time is
infinite and
P(N
t
= n)=e
−λt
(λt)
n
n!
.
The standard Poisson process can be redefined as follows (see e.g., C¸ inlar
[188]): it is a counting process without explosion (i.e., T = ∞) such that
• for every s, t ≥ 0ther.v. N
t+s
− N
t
is independent of F
N
t
,
• for every s, t,ther.v.N
t+s
− N
t
has the same law as N
s
.
or, in an equivalent way, a counting process without explosion whose
increments are independent and stationary.
-
6
0
T
1
T
2
T
3
tT
4
T
5
1
2
3
N
t
=4
5
•
•
•
•
•
Fig. 8.1 Poisson process
