Jackson Mark. Machining with Abrasives

Подождите немного. Документ загружается.

Increasing ﬂuid density, r

, reduces particle velocity.

Increasing ﬂuid viscosi ty, m

, is beneﬁcial, provided pressure losses inside the

mixing tube are not excessive.

For AWJ, maximizing the abrasive ﬂow rate is always beneﬁcial, as long as the

ﬂuid to abrasive ﬂow ratio

is maintained under 50:1.

Changing abrasive particle size, within the limits in (9.13), at a constant abrasive

ﬂow rate, alters the number of abrasive particles per second, but does not change

the total energy stored, nor average particle velocity, v

Only very short mixing tubes lead to reduced particle velocity. At the typical

L/d  300, the effects of tube length and particle size cancel out.

A typical commercial AWJ system, similar to Fig. 9.1 , uses a 0.25 mm oriﬁce,

D ¼ 0.75 mm and L ¼ 75 mm mixing tube, ﬁltered water, and garnet abrasives.

For such a system, (9.13) becomes

 0:025

ﬃﬃﬃﬃﬃ

1  e

1=480d



& d

ﬃﬃﬃﬃﬃ

b4:8; (9.14)

which is a more accur ate estimator

b50than (9.11). At 400 MPa, and

provided that nominal particle size d < 0.24 mm and, then the average particle

velocity at the instant of impact is v

 500 m/s. This result and the closed-form

solution in (9.13) are in agreement with the numerical estimation in [57] and other

analytical and experimental results [58], but it is simpler and more intuitive to use.

9.2.4 Research Directions

A proper analysis of AWJ or AAJ would require the solution of a number of

coupled partial differential equations for the three-phase ﬂuid dynamics of a

mixed ﬂow of water, air bubbles (for AW J; or air with moisture content, for AAJ)

and solid abrasive particles; along with the contact and impact solid dynamics

among the particles, and between particles and the mixing tube wall; plus

thermodynamics and heat transfer, multi-body kinematics, and statistical mechan-

ics. The ﬂuid dynamics is viscous compressible, rotational, entropic, turbulent,

mixed-phase with moving, deformable, discontinuous, and randomly-moving

boundaries. The solid dynamics involves elastic-plastic multi-b ody collisions,

fracture, fragmentation, and all sorts of constitutive materials behaviors; and subject

to random body motions and weakly deﬁned boundary conditions. Al l those

behaviors are coupled in an exceedingly nonlinear manner that precludes the

possibility of any closed-form solution, even in some statistical sense. It is safe to

say that a problem like AWJ is not solvable, from ﬁrst principles of continuum and

statistical mechanics. Even with current advances in computational methods, and the

exponential growth in computing power and high-performance computers, this

problem remains a challenge, and there may be decades before it can be simulated

numerically with satisfactory realism.

9 Impact Abrasive Machining 395

Efforts towards more advanced analysis of jet generation and characteristics are

a huge volume of research, as reviewed in [37, 59], and include:

Development of high-pressure equipment and systems;

Optimization of oriﬁce and nozzle design and alignment;

Characterization of abrasives size, shape, and velocity distribut ions;

Estimation and minimization of pressure drop, energy and momentum losses,

and other inefﬁciencies during the mixing process;

Particle acceleration models, similar to that in (9.13);

Particle fragmentation and size reduction; and

Wear of the mixing (focusing) tube and its effect on jet characteristics; to name

but some of the research topics. Most of those issues are relevant to machine and

nozzle design. Once a speciﬁc machine or cutting head is selected, those para-

meters cannot be altered. Hence, for production and process planning of AWJ,

(9.13) remains a more useful model of controllable process variables.

There are signiﬁcant efforts to simulate the jet ﬂow using Computational Fluid

Dynamics (CFD). These include [59–61] solv ing the 2D axi-symmetric problem for

the axial and radial velocity distributions of the ﬂuid jet, then ﬁtting the numerical

solution to an equation, which is then used to estimate particle velocity. Similar

treatments were reported in [62, 63]. In [64] random position and velocity of

particles were simulated by mean of a fractal point set, without physical justiﬁca-

tion why abrasive jets may have a fractal dimension, or why their motions follow

any speciﬁc statistical distribution. Further, at the current state of computational

abilities, it is still difﬁcult to simul ate the multi-physics of the coupled motion of

both ﬂuid and particles, as they interfere with the behaviour of each other in a

highly nonlinear manner.

There have been extensive efforts in developing techniques for experimental

measurement of pure waterjet and abrasive particle velocity inside the AWJ [37] and

AAJ [56]. Techniques include magnetic and inductive methods, reverse estimation

from impact crater depth or from impact force measurement, various types of laser

(interference, time of ﬂight, or Doppler) velocity meters, or using ultra-high speed

photography. All techniques include measurement uncertainties, difﬁculties in

discriminating between ﬂuid and particle, and they only detect average behaviour

outside the nozzle, i.e. not the axial and radial distributions inside the nozzle. Results

from experimental measurements are in agreement with (9.13).

9.3 Material Removal by Impact

In a typical AWJ machine, abrasive particles mass ﬂow rate could be ~10 g/s. For

garnet particles, and nominal average size ~0.15 mm, this amounts to ~10

particles

per second; which may seem a huge number, but it is only one particle per

microsecond. At impact velocity ~500 m/s, the full process of particle indentation

and rebound lasts a fraction of ms. The jet spreads over ~1 mm spot size, ~40 the

396 Y.M. Ali and J. Wang

area for a single particle impact. Traverse (workpiece displacement) speed is

typically 1–100 mm/s, whi ch is negligible compared to impact velocity, and only

fraction of a mm/ms – which is negligi ble compared to particle size.

From this quick calculation, it is reasonable to treat AWJ as a sequence of single-

particle impacts: each particle indents, removes material, and rebounds away from

the target as an independent event, without interference from other particles or from

workpiece motion. The ﬁnal effect of an AWJ cut is the geometric superposition of

craters produced by all particles. This may not be simple to calculate due to the

random variation in particles sizes, shapes, and times of their arrival at particular

spots on the target. There may also be interference among incoming and rebounding

particles, removed debris, or the waterjet. However, it should be possible, in

principle, to develop an average model to account for all those perturbations, if

the effect from single particle impact is known with reasonable conﬁdence.

In AWJ, all forms of irregular particle shapes can be found in the abrasive jet.

Rigid body rotation of the particles inside the jet stream, sliding and rolling motion

during impact on the target, and localized deformation and fragmentation of the

particles during impact, all provide additional uncertainty. It is not possible to

estimate the distribution of real particle geometries at the instant of impact on the

surface. It is assumed that all those random effects balance, and some “average”

abrasive particle behavior is modeled by spherical impact. The main advantage of

such assumpt ion is that the contact mechanics of a sphere is one of the most studied

and understood [65–69].

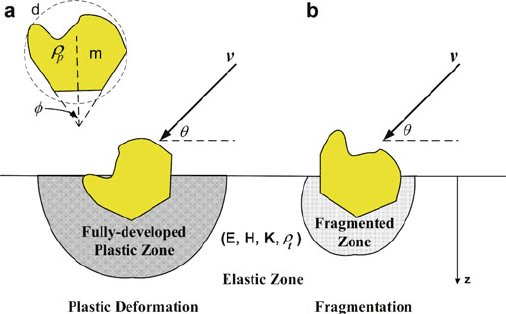
In general, material response to impact is described either as ductile or britt le

erosion, as shown in Fig. 9.4. Ductile erosion is relevant to metals and similar

materials that are capable of signiﬁcant plastic deformation. Brittle erosion applies

to ceramics, glasses, and hard metals that crack and fragment under impact.

Fig. 9.4 Ductile and brittle erosion modes

9 Impact Abrasive Machining 397

9.3.1 Ductile Erosion

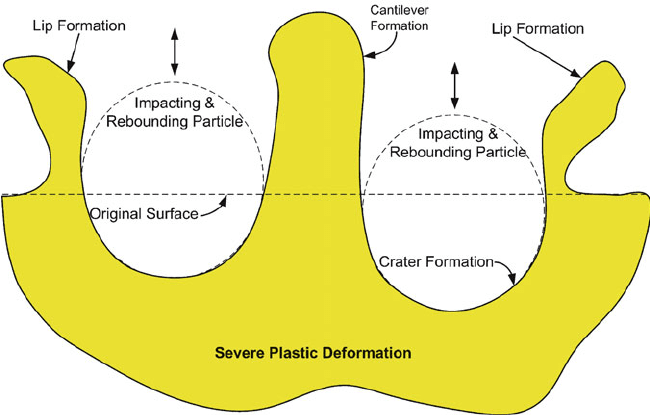
Considering a rigid particle hitting a smooth ﬂat surface, as shown in Fig. 9.4, the

general oblique impact condition can be decomposed into normal (indentation-like)

and tangential (scr atching-like) components. For normal impact, y ¼ 90



, the

particle pushes the surface down, and material beneath is compressed. As indenta-

tion continues, material in the high compression zone escapes pressure, by moving

sideways, then upward towards the free surface. After the particle rebounds, a

permanent crater is left on the surface, and excess lips (elongated ﬂakes) are

formed. The successive application of numerous particles results in cantilever

formations that are easy to separate from the mother material (Fig. 9.5).

If an abrasive particle has mass, m

, and initial impact velocity, v, its stored

kinetic energy is ½ m

. Upon impact on the target surface, some fraction of the

kinetic energy is consumed in displacing the target surface and forming a perma-

nent crater, such that [1]

ðvsinyÞ

HAðxÞdx; (9.15)

where H is target material hardness, and h is indentation or crater depth. The

projected area function, A(x), is unknown, except for some regular shapes. However,

exact expre ssion for that function is not required, by noting that crater volume, V,is

Fig. 9.5 Material displacement and removal by successive particles impact

398 Y.M. Ali and J. Wang

V ¼

AðxÞdx: (9.16)

Consequently, the volume removed by impact, V

,is

ðv sin yÞ

; (9.17)

which is a relative estimate of material removal in ductile materials by normal

impact.

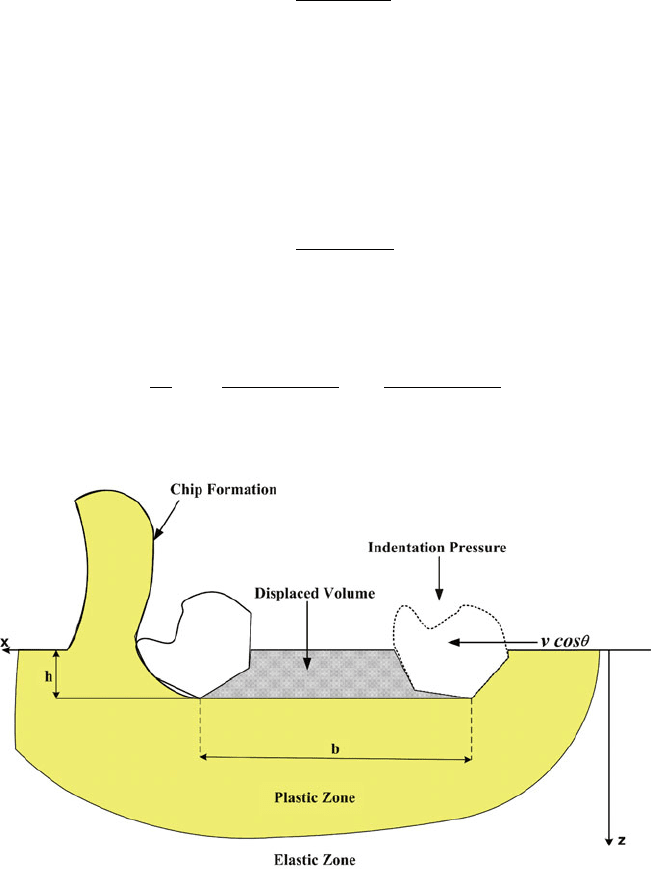
During tangential (scratching) motion, as shown in Fig. 9.6, shear stresses increase

at the expense of compressive stresses. Stresses become tensile on the trailing edge

and more compressive on the leading edge of the particle. Crater formation includes

the ploughing effect from sliding and friction. The volume removed in this case, as in

(9.17), is also proportional to the kinetic energy of the particle:

ðv cos yÞ

: (9.18)

The combined volume removed due to oblique impact is obtained by addition of

the normal and tangential components:

ðv sin y 

ðv cos y 

(9.19)

Fig. 9.6 Material removal by tangential (scratching) abrasive motion

9 Impact Abrasive Machining 399

where k

and k

are experimental coefﬁcients, and v

and v

are threshold velocities

below which no material removal can occur. The erosion model in (9.19) is similar

to that proposed by Neilson and Gilchrist [70], which is a generalization of earlier

erosion models by Finnie [71] and Bitter [72, 73]. There are many other ductile

erosion models, e.g. [74], as reviewed in [31].

9.3.2 Brittle Erosion

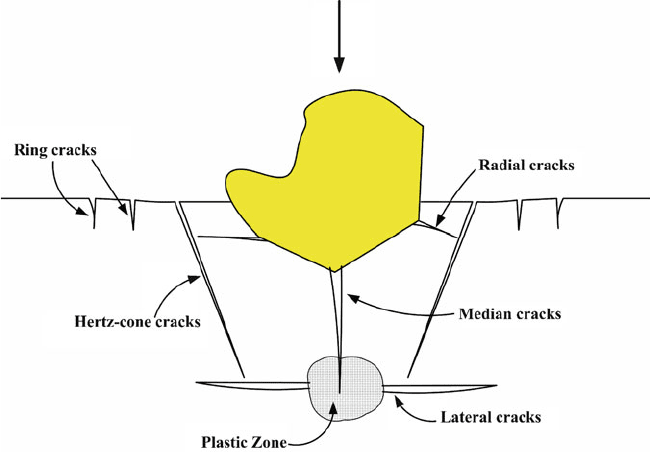
When a target material is not capable of signiﬁcant plastic deformation, it responds

to impact loads by fracture, forming cracks, and fragmentation of the affected zone.

Cracks can be of the ring type (due to elastic stress waves [75]), conical type (due to

quasi-static tensile failure [76]), radial, median, and lateral type (due to stress

redistribution in the plastic zone at the crack-tip during loading and unloading)

[77–79], as shown in Fig. 9.7. The estimation of those brittle fracture mechanisms

require some assumptions about ﬂaws sizes and their distribution; the location, size,

and growth rate of the various cracks; and the interactions among various cracks.

Such models eventually resort to experimental data for quantitative veriﬁcation.

All brittle erosion models can be reduced to a causality formula of the form:

/ r

; (9.20)

Fig. 9.7 Brittle erosion by cracking and fragmentation

400 Y.M. Ali and J. Wang

where r

is particle density, d is particle size, v its impact velocity, and H, K and E

are hardness, fracture toughness and Young’s modulus of the target material,

respectively. Depending on the speciﬁc fractu re model being assumed, the expo-

nents in (9.20) are found to be: q

¼ 0–1.6, q

¼ 3–4.2, q

¼ 2–3.2, q

¼ –1.4 to

1, q

¼2to1, and q

¼ 1–1.25. For quantitative accuracy, it is appropriate to

evaluate those exponents experimentally for each speciﬁc particle-target materials

combination.

9.3.3 Uniﬁed Erosion Model

It is noted that all ductile erosion models, e.g. (9.19), predict that V

/ v

, while

brittle erosion models, e.g. (9.20), predict that V

/ v

. This is in disagreement with

experimental observations, where it is found that the velocity exponent is dependent

on material property, and is 2.2–2.5 for metals and 2.6–3 for ceramics. The

deviation between models and experiment is understood, because of the fact that

no real material is absolutely ductile or absolutely bri ttle, and some interpolation

between the two extreme idealizations is needed. As impact velocity is the most

important variable in impact erosion, error in estimating the velocity exponent can

degrade the accuracy of all those models.

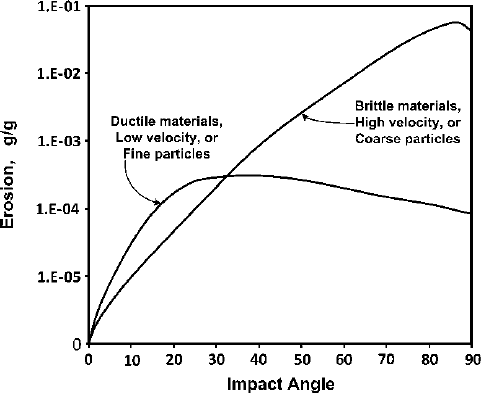
Further, it is observed that maximum erosion occurs at an impact angle, y

max

,of

near 90



for brittle materials at higher velocity or using coarser abrasive particle

(Fig. 9.8). The peak erosion angle is 20–30



for ductile materials at lower impact

velocity or using ﬁner particles. The above models are unable to explain this peak

shifting. As impact angle is the second most important factor affecting material

removal, this represents an added source of inaccuracy.

In a yet to be published work, the authors present a uniﬁed erosion model that is

applicable to ductile and brittle materials alike. It is able to interpolate between the

extreme cases of ideal plasticity and ideal fracture, and provide a more realistic

representation of real engineering materials. The model can explain the variable

velocity exponent, the peak erosion angle shifting, the effect of various material

properties, the effect of particle size and shape, and other effects such as ductile-

brittle transition and size effect. According to such a model

¼ðA

sin

y þ A

cos

yÞv

þðA

sin

y þ A

cos

yÞv

; (9.21)

where

¼ k

a þ bH

; A

¼ k

ð1  10

DÞ

2HD



3=2

; A

¼ A

; A

¼ A

;

D ¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2EHð1 þ 2e

; (9.22)

9 Impact Abrasive Machining 401

a and b are material constants relating dynamic to quasi-static hardness, e

and

are fracture and elastic strains (material properties of the target material),

and k

–k

are experimental parameters. For speciﬁc abrasive particle-target mater i-

als combinations, it is better to use (9.21), with A

–A

determined experimentally.

9.3.4 Material Removal by Abrasive Jet

For ductile materials, Hashish [80] proposed an AWJ machining model based on

the initial Finnie model [71]. This was later improved [81] based on the revised

model by Finnie and Sheldon [82]. Numerous models (e.g. [83 – 85]) have been

proposed over the years, and they are all fundamentally similar, and are based on

some modiﬁcation of ( 9.19). For brittle materials, various models for AWJ machin-

ing have been proposed (e.g. [86–88]), and they are all based on the quasi-static

fracture models developed in [77–79], as generalized by (9.20). All such AWJ

machining models are subject to limitations imposed by their parent impact erosion

models, as discussed in Sect. 9.3.3. Speciﬁcally, these models cannot predict the

material-dependent velocity exponent, erosion peak angle shifting due to particle

size, nor the ductile-brittle transition experience in real material behaviour,

e.g. Fig. 9.8.

The average velocity of the abrasive particle, as it exits the nozzle, can be

estimated from (9.13). The average target material removal due to impact by the

abrasive particle can be estimated from (9.21). For a jet stream containing

Fig. 9.8 Peak erosion angle shifting with material and impact conditions

402 Y.M. Ali and J. Wang

numerous abrasive particles, it is suitable to take the time derivative of (9.21), and

express the material removal rate per abrasive particle mass ﬂow rate, as

E ¼

dDU

; (9.23)

where d is depth of cut, D is nozzle diameter (approximately equal to width of cut,

for small standoff distance), and U is traverse speed of the jet on the surface of the

target material. Typical removal rates usin g AWJ cutting are listed in Table 9.2.

For a given nozzle diameter and abrasive ﬂow rate (as deﬁned in Sect. 9.2.3), it is

seen that volume removal rate is conserved. There is direct trade-off between depth

of cut and traverse speed: increasing traverse speed decreases the depth of cut. The

only way to increase depth of cut at constant traverse speed, abrasive ﬂow rate, and

nozzle diameter is by increasing the erosion rate itself, as dictated by (9.21). For a

given target material, maximizing erosion is achieved by either maximizing the

impact velocity, v in terms of (9.13), or by selecting the optimum impact angle for

peak erosion, as in Fig. 9.8.

Using (9.23), it is possible to estimate a typical depth of cut due to AWJ, using

any jet parameters, and for any target material. Real material removal by AWJ is

more complicated than described above. As the AWJ traverses across a target work-

piece, a kerf is gradually developed. This process was extensively studied using

high-speed camera visualization techniques [89, 90], and is outlined in Fig. 9.9.

Initially, abrasive particles impact normal to the workpiece surface, and material

removal is similar to Fig. 9.5. However, as the jet proceeds and some material is

removed, a ramp is formed: abrasives then approach tangential impact as in

Fig. 9.6. As the jet continues its traverse, a step is formed, and a condition of

normal impact is restored. The cycle continues repeatedly, until a steady state

condition is reached; a kerf proﬁle, having a step-wise ramp shape, is maintained

for the rest of the cut.

As can be seen from the right-most view in Fig. 9.9, under steady state conditions,

some particles impact on the material at near normal (indentation-like), while other

impact at near tangential (scratching-like) direction. For historic reasons, Hashish

[80, 89] refers to the ﬁrst condition as “deformation wear” and to the latter as “cutting

wear”. In reality, material is removed during both cases, but the mechanism varies, as

shown in Figs. 9.5 and 9.6. The importance of kerf formation can be understood from

inspection of Fig. 9.8. It is seen that material removal rate is maximized for brittle

Table 9.2 Typical removal rates by AWJ for depth d ¼ 25 mm

Material

Speed,

U (mm/s) Material

Speed,

U (mm/s) Material

Speed,

U (mm/s)

Carbon steels 0.5–2 Aluminum 0.3–3.5 Glass 35

Alloy steels 0.2–1 Titanium 0.2–2 Quartz 0.3

Stainless steels 0.2–1.5 Nickel alloys 0.04–0.15 Alumina 0.05–0.3

9 Impact Abrasive Machining 403

materials when particles impact near normal. For ductile materials, material removal

is maximized when particles impact at 20–30



to the surface.

The geometry in Fig. 9.9 results in particles impacting at angles whose average is

the optimum angle for neither ductile nor brittle materials. At present, there is no

satisfactory theory to estimate the equivalent average impact angle and kerf formation,

in terms of process variables. However, from geometry, the kerf can have a steeper

ramp when the traverse speed is lower. This, in turn, reduces the average impact angle,

and brings it closer to the scratching mode. Therefore, it is more efﬁcient to cut ductile

materials at slower traverse speed (smaller effective impact angle), while faster

traverse speed (larger effective impact angle) is more productive for machining

brittle material. However, as seen from (9.23), there is interdependence between

traverse speed and depth of cut. A better alternative to enhance (and control) the

effective impact angle by tilting the nozzle, as will be explained in Sect. 9.4.1.

From the circular cross-section of the jet, it is clear that more abrasive particles

impact near centerline of the cutting path than near its edge. Moreover, there is

greater loss of kinetic energy near edge of the jet, due to abrasive particle deﬂec-

tions, inter-particle collisions during rebound, and interference from the ﬂuid jet.

This results in tapering of the cut groove, as shown in Fig. 9.10, and the ﬁnal cut can

be divided into three distinct zones [91, 92]:

Smooth cut zone: where the tapering effect is relatively small and surface

roughness of the produced wall is reasonably ﬁne.

Rough or striation cut zone: where the tapper angle is signiﬁcantly larger, and

signiﬁcant scratch marks and rough wall surface is observed.

Pocket formation: where material removal is due to random colli sions from

rebounding particles.

Fig. 9.9 Step formation during abrasive jet traverse

404 Y.M. Ali and J. Wang