Иванов А.Н. Построение эконометрических моделей и прогнозирование в MS Excel: сборник лабораторных работ

Тема лабораторной работы: Матричная алгебра в идентификации модели множественной линейной регрессии.

14из17

Анализ качества модели множественной линейной регрессии.

Интервальное оценивание параметров уравнения множественной линейной регрессии.

Лектор: к.ф.-м.н., доцент Иванов Андрей Николаевич

Кафедра «Прикладная математика» ДВГУПС

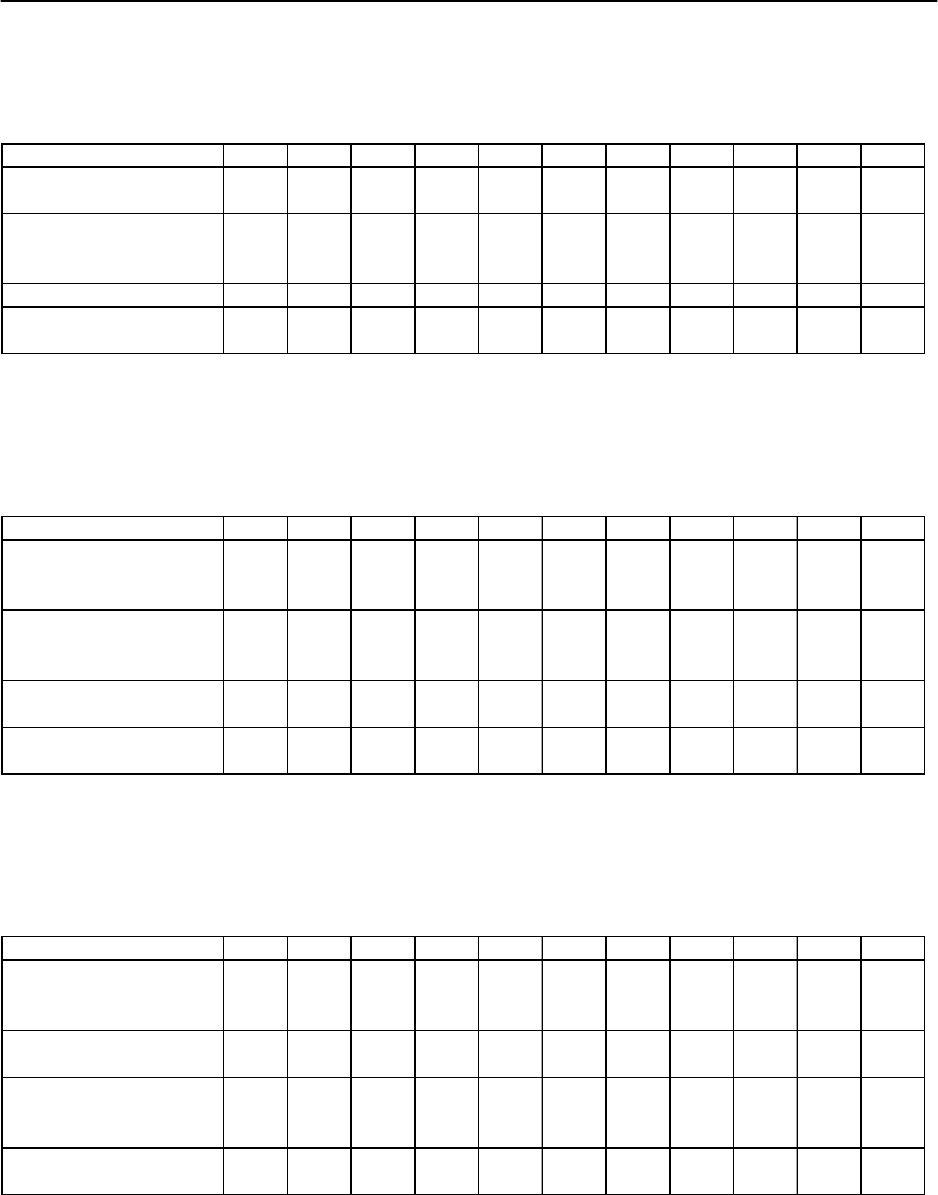
12. Данные по объему продаж различных марок краски для волос. Осуще-

ствить точечный прогноз при значениях факторов равных 112 % от их сред-

них значений.

1234567891011

60359012080404582705065

Кол-во оттенков (x

3

),

шт.

20 12 25 35 30 25

1

25 40 34 30 35

12

Цена краски (x

2

), руб.

15 16 10

54108

22

№ марки

Объем потенциальных

покупат. (x

1

), тыс. чел.

15 20 12 10 13 18

Объем продаж краски

д/волос (y), шт.

573692

13. Данные общего количества студентов, получивших зачет автоматиче-

ски по одной дисциплине, за 11 лет. Осуществить точечный прогноз при зна-

чениях факторов равных 113 % от их средних значений.

1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005

10 9 9

14

Кол-во проведенных

практ. занятий (x

3

), шт.

10 9 7 8 10 10 9 8

Год

Кол-во студентов,

получивших зачет

автоматом (y), чел.

1726101268109

Кол-во защищенных

лаб. работ (x

1

), шт.

25 25 10 45 5

1

40

15 15 14

5030 50 60 30

13 16 1513 14 16 11

Кол-во проведенных

лекций (x

2

), шт.

14. Студенты, поступившие на коммерческую специальность, динамика

за 11 лет. Осуществить точечный прогноз при значениях факторов равных

114 % от их средних значений.

1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005

Кол-во поданных

заявлений (x

3

), шт.

25

Общий проходной балл

(x

1

)

200

Кол-во студентов,

поступивших на

коммерч. спец. (y), чел.

20

170 185 190

35 29 36 33

189

28 3026 24

187 191

22 26

176 188

Средний балл,

набранный при

поступлении (x

2

)

193 182 184

180185 190 195 195 190 185 185190 185

22 2318 19 21 2321 20 19 20

Год

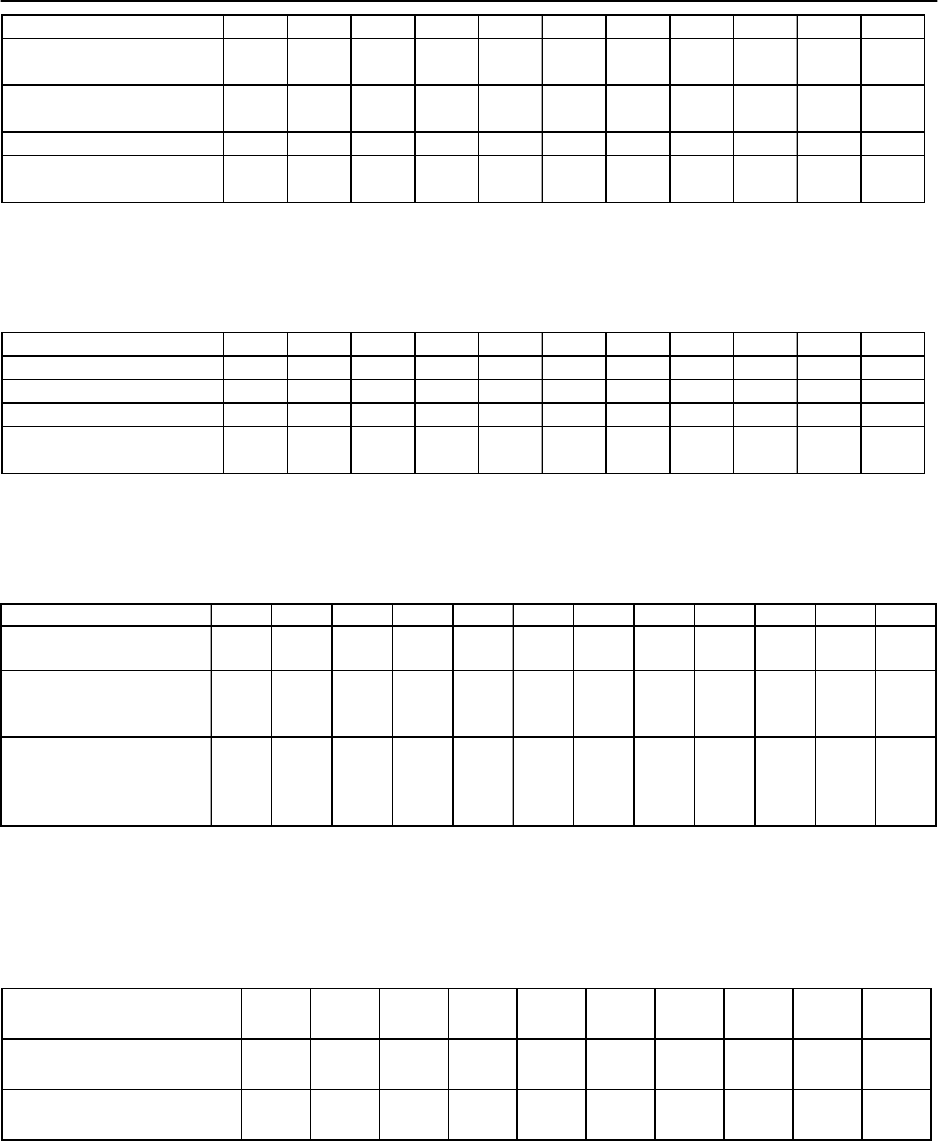
15. Объем производства товара, динамика за 11 лет. Осуществить точеч-

ный прогноз при значениях факторов равных 115 % от их средних значений.

Тема лабораторной работы: Матричная алгебра в идентификации модели множественной линейной регрессии.

15из17

Анализ качества модели множественной линейной регрессии.

Интервальное оценивание параметров уравнения множественной линейной регрессии.

Лектор: к.ф.-м.н., доцент Иванов Андрей Николаевич

Кафедра «Прикладная математика» ДВГУПС

1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005

20 21 23 21 22 24 23 23 22 25 24

556

Объем продаж (x

3

), шт.

530 539 534 525 530 530 532 531 540 545

110 10098 95 100 110

Себестоимость (x

1

),

руб.

Издержки (x

2

), руб.

90 93 95

574

99

589563 567 562 578

Год

Объем производства

товара (y), шт.

556 560 564 554 560

98

16. Динамика ВВП в России, данные за 11 лет. Осуществить точечный

прогноз при значениях факторов равных 116 % от их средних значений.

1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005

215 296 372 324 354 351 426 443 504 489 466

90 87 86 86 91 99 104 112 125 131 140

125 209 286 238 263 252 322 331 379 358 326

Год

ВВП (y), млн дол.

261 283 290 315

Издержки (x

3

),

млн дол.

190 200 60 210 220 237 254

Экспорт (x

1

), млн дол.

Импорт (x

2

), млн дол.

17. Имеются данные за 2000 год. Осуществить точечный прогноз при

значениях факторов равных 117 % от их средних значений.

янв. фев. март апр. май июнь июль авг. сен. окт. нояб. дек.

466 436

Объем ВВП (у),

млн руб.

212 302 372 324

336

Месяц

292 309

354 351 426 443 504 489

239 237 226 257

689

247

414 395454 472 501 448

310

413 449 450 680

273

730

188 198

Объем пром.

продукции (х

1

),

млн руб.

Производство

продуктов в

животноводстве (х

2

),

млн руб.

18. Даны данные крупнейших торговых компаний Франции (1994г., в

млрд. франков). Осуществить точечный прогноз при значениях факторов

равных 118 % от их средних значений.

Товарооборот

(y)

, млрд

франков

Собственный капитал

(x

1

), млрд франков

Чистая прибыль (x

2

),

млрд франков

3,6 0,90,7

23 22,3 19,7

4,6

56,5 34,7 34

0,8

1,1 1,1 0,51,2

0,1 0,20,1 0,3 0,5 0,3 000,3

2

17,1 15,7 15 14,2

1,5

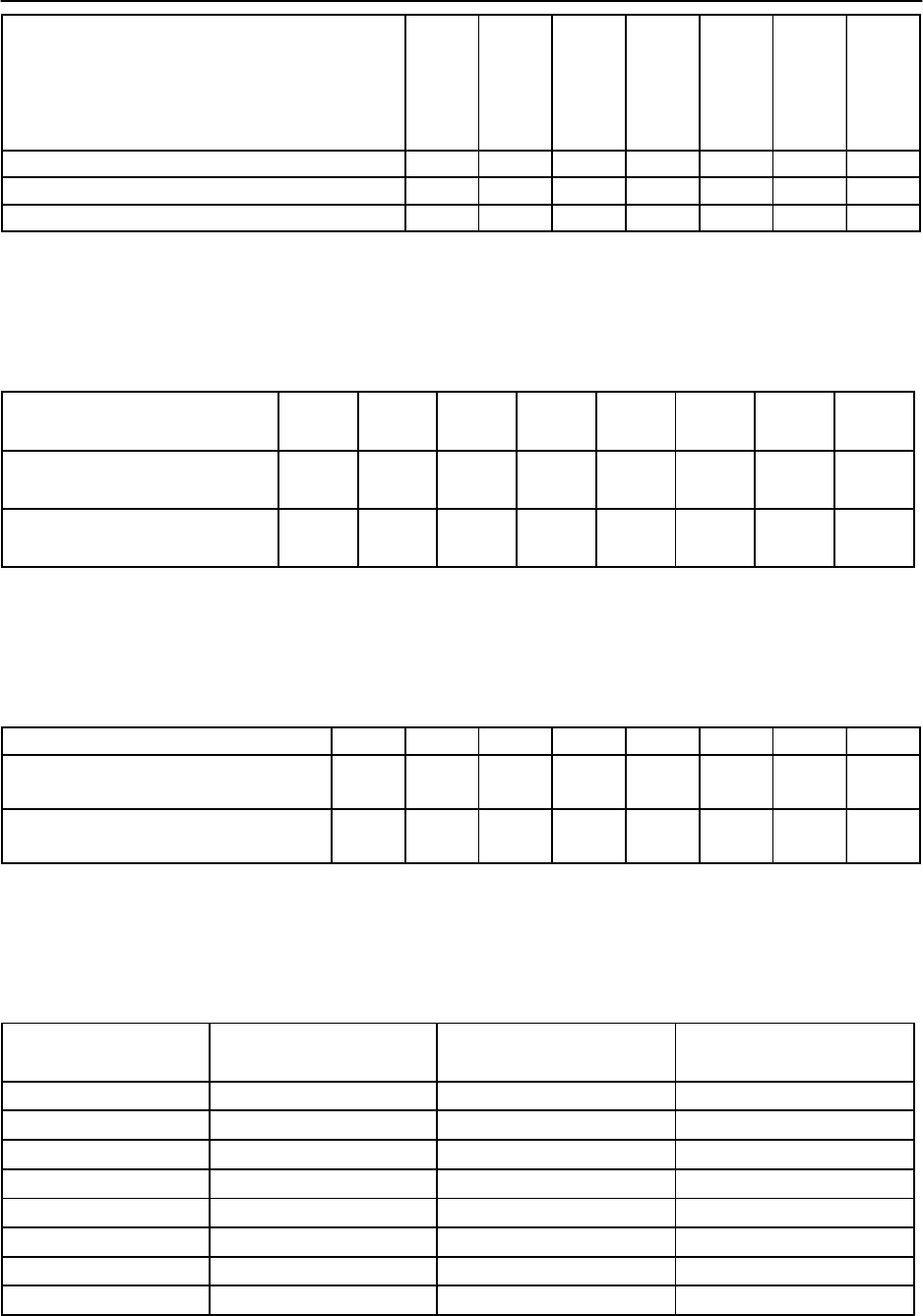
19. Рейтинг стран по показателям туристического сервиса, 2004 г. Осуще-

ствить точечный прогноз при значениях факторов равных 119 % от их сред-

них значений.

Тема лабораторной работы: Матричная алгебра в идентификации модели множественной линейной регрессии.

16из17

Анализ качества модели множественной линейной регрессии.

Интервальное оценивание параметров уравнения множественной линейной регрессии.

Лектор: к.ф.-м.н., доцент Иванов Андрей Николаевич

Кафедра «Прикладная математика» ДВГУПС

27 6 29223530 8

15 6 28163329 5

14 8 29113233 3

Австралия

Австрия

Багамы

Страна

Принято туристов (y), млн руб.

Доходы (x

1

), млн руб.

Затраты (x

2

), млн руб.

Бельгия

Венгрия

Бермуды

Бразилия

20. Финансово-экономические показатели крупнейших французских бан-

ков. Осуществить точечный прогноз при значениях факторов равных 120 %

от их средних значений.

2,72,710,13,1 2,1 1,4 3

36,7 40,3 14,2 3,335 34,6 26,9 30,5

739,6 408,8 387,1 251,21193 1088 1021 942,2

Собственный капитал

(x

1

), млн фр.

Чистая прибыль (x

2

),

млн фр.

Оборот (y), млн фр.

21. Основные социально-экономические показатели стран содружества в

2004г. («Общество и экономика» № 4, 2005). Осуществить точечный прогноз

при значениях факторов равных 121 % от их средних значений.

110,2 110,1 111 108,4 109,4 107,1 107,3 107,1

Валовая продукция с.-х. (х

2

),

млрд дол.

ВВП (у), млрд дол.

115,6

104,6 114,5 112,9 93,5

103,7 106,9 106,1

100,1 104,1 120,4 101,6

110,1102,1

Промышленная продукция

(х

1

), млрд дол.

103,4105,7

22. Региональная структура внешней торговли Украины в 1995 году

(млн.$). Осуществить точечный прогноз при значениях факторов равных

122 % от их средних значений.

Экспорт (х

1

), млн $ Импорт (х

2

), млн $

Региональные

рынки

Товарооборот (у),

млн $

Европа

ЕС

ЕАСТ

АСЕАН

Америка

НАФТА

Африка

Австралия

5602,3

3028,8

1053

378,8

1365,8

877,9

243,6

45,6

2644,4

1283,4

506,2

329,9

742,2

557,9

186,4

25,8

2957,8

1745,4

546,8

48,9

623

320

57,2

19,8

Тема лабораторной работы: Матричная алгебра в идентификации модели множественной линейной регрессии.

17из17

Анализ качества модели множественной линейной регрессии.

Интервальное оценивание параметров уравнения множественной линейной регрессии.

Лектор: к.ф.-м.н., доцент Иванов Андрей Николаевич

Кафедра «Прикладная математика» ДВГУПС

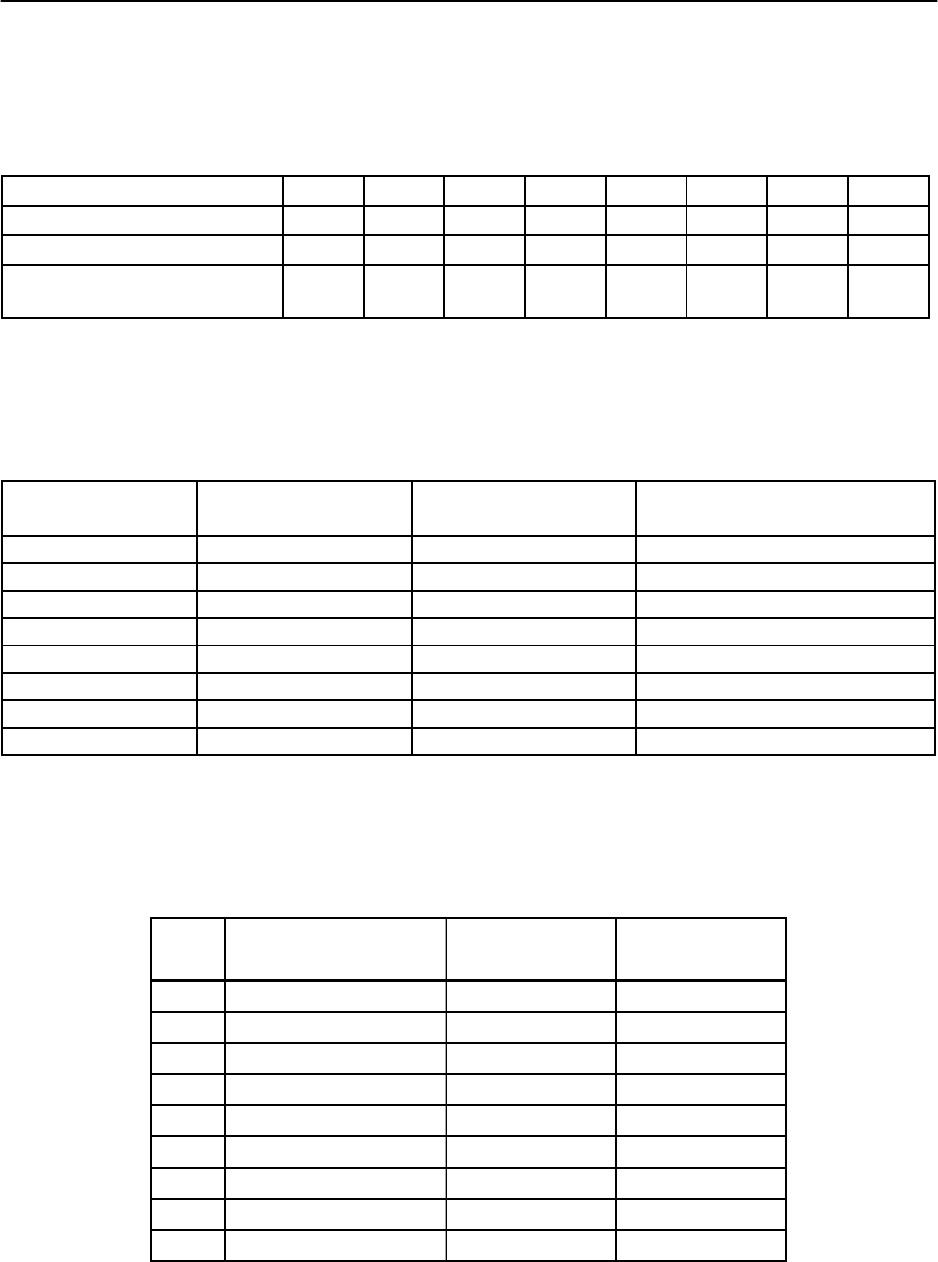
23. Из журнала «МЭ и международные отношения», 2002, № 8, с.63 взяты

данные доли предприятий с иностранным участием во внешней торговле

КНР. Осуществить точечный прогноз при значениях факторов равных 123 %

от их средних значений.

1990 1991 1992 1995 1996 1997 1998 1999

12,6 16,8 20,4 31,5 40,7 41 44 45,5

23,1 26,5 32,7 47,7 54,5 54,6 54,7 51,8

47 48,7 48,421,3 26,4 39,1 47,3

Год

Экспорт (х

1

), %

Импорт (х

2

), %

Внешнеторговый

оборот (у), %

17,4

24. Внешняя торговля России с некоторыми зарубежными странами в

1993 г. Осуществить точечный прогноз при значениях факторов равных

124 % от их средних значений.

2005 1367

653

Внешнеторговый оборот

(у), млн руб.

1100

6536

1851

871

1646

1074

Япония

Страна

Экспорт (х

1

),

млн руб.

Импорт (х

2

),

млн руб.

3353

5074 5142

2629 1106

1057

Великобритания

Германия

Италия

Бельгия

Нидерланды

Франция

США

466

979 431

1556 899

1997 2304

763

2648

25. Некоторые показатели экономического развития КНР. (Журнал «МЭ и

международные отношения», 2002, № 8, с.65). Осуществить точечный про-

гноз при значениях факторов равных 125 % от их средних значений.

1985

1986

1988

1989

1990

1991

1992

1993

1994

11,311

52,5

84,9

62,1

4,612

3,801

9,305

14

Год

Прирост ВВП (у),

млрд дол.

12,116

8,111

Экспорт (х

1

),

млрд дол.

115,7

Импорт (х

2

),

млрд дол.

42,2

63,8

80,6

104

42,9

47,5 55,3

71,8

27,42

30,91

59,1

53,4

121

91,713,32

11,663

Тема лабораторной работы: Нелинейные регрессионные модели: идентификация, прогноз, графическое представление.

1из9

Лектор: к.ф.-м.н., доцент Иванов Андрей Николаевич

Кафедра «Прикладная математика» ДВГУПС

Л

А

Б

О

Р

А

Т

О

Р

Н

А

Я

Р

А

Б

О

Т

А

№

5

Т

е

м

а

:

Нелинейные регрессионные модели: идентификация, прогноз, гра-

фическое представление

.

Ц

е

л

ь

:

1. Научиться строить нелинейные регрессионные модели. 2. Уметь

по построенным моделям осуществлять точечный прогноз и графически реа-

лизовывать построенные модели.

Ф

о

р

м

а

о

т

ч

е

т

н

о

с

т

и

.

Представить преподавателю подробное решение за-

дачи с выводами в MS Excel. Оформление должно быть аналогично разо-

бранному примеру. Письменно ответить на контрольные вопросы на рабочем

листе MS Excel после решения задачи. Вариант работы определяет препо-

даватель.

Замечание 5.1. Ячейка, содержащая формулу, будет отмечена серым цве-

том.

Задача 5.1. Даны результаты разнонаправленной динамики социально-

экономического развития в районах России за 2004г. (Источник: Экономист.

– 2005. – №3) (рис. 5.1).

0,6 1 1,8 2,1 1,6 1 0,7

Уровень безработицы (х

2

), %

82,01

Инвестиции в основной

капитал (х

1

), тыс. руб.

ВРП на душу населения (у),

тыс. руб.

218,1 78,68

36,49

71,33

18,55 14 83,93 15,52 8,92 10,78

88,13 299,4 78,9

Рис. 5.1

Необходимо:

1) методом наименьших квадратов получить систему нормальных урав-

нений для двухфакторной нелинейной регрессионной модели вида

ε

+++=

22110

xaxaay

;

2) определить коэффициенты системы нормальных уравнений, используя

исходные данные;

3) решить систему нормальных уравнений с помощью надстройки MS

Excel Поиск решения…;

4) записать полученное уравнение нелинейной регрессии;

5) осуществить точечный прогноз при средних значениях обоих факто-

ров;

6) дать графическую интерпретацию построенной регрессионной модели.

А

л

г

о

р

и

т

м

р

е

ш

е

н

и

я

з

а

д

а

ч

и

1. Применим метод наименьших квадратов для составления системы

нормальных уравнений.

1.1. Составим общую ошибку

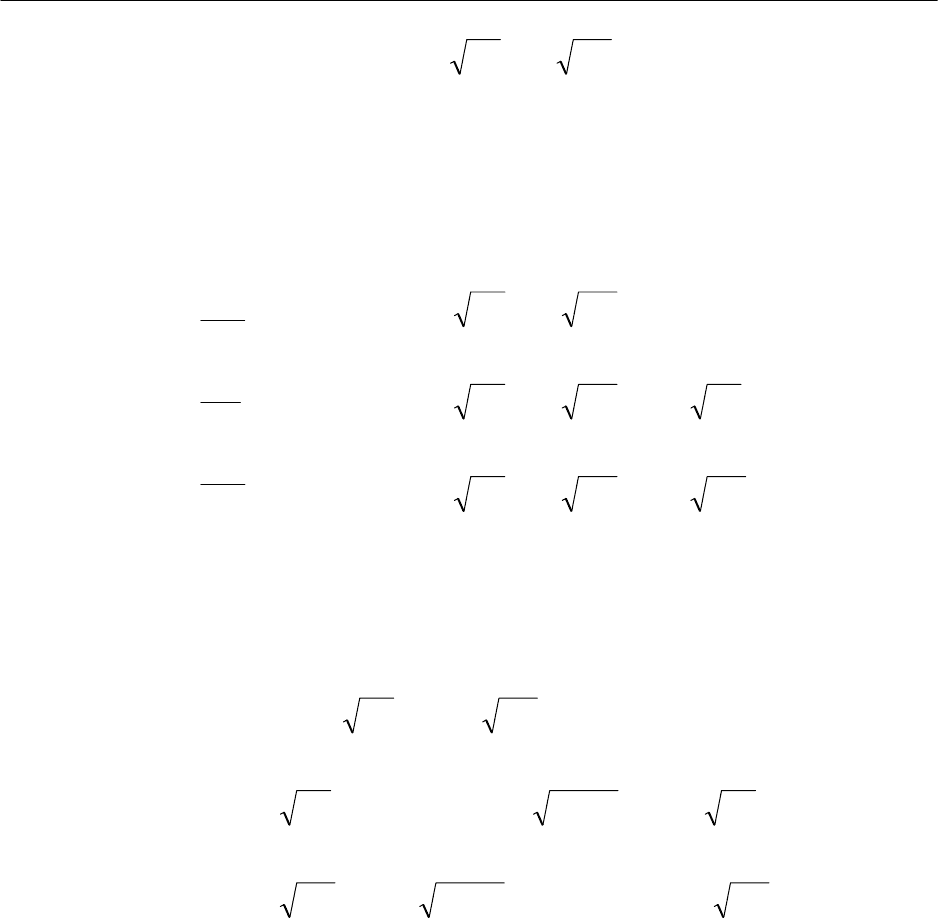
Тема лабораторной работы: Нелинейные регрессионные модели: идентификация, прогноз, графическое представление.

2из9

Лектор: к.ф.-м.н., доцент Иванов Андрей Николаевич

Кафедра «Прикладная математика» ДВГУПС

()()

∑

=

−++=

n

i

iii

yxaxaaS

1

2

22110

.

1.2. Используя необходимое условие экстремума функции многих пере-

менных, составим систему алгебраических уравнений для нахождения пара-

метров модели:

⎪

⎩

⎪

⎨

⎧

=

∂

=

∂

=

∂

.0

,0

2

1

0

a

S

a

S

a

S

()

⎪

⎩

⎪

⎨

⎧

=⋅−++

=−++

∑

=

.02

,02

2

1

22110

1

22110

1

22110

i

n

i

iii

i

n

i

iii

n

i

iii

xyxaxaa

yxaxaa

1.3. После преобразований, получаем систему нормальных уравнений для

исходной двухфакторной нелинейной регрессионной модели:

⎪

⎩

⎪

⎨

⎧

=++

∑∑∑∑

∑∑∑

====

===

.

,

1

2

1

22

1

211

1

20

1

212

1

11

1

10

11

22

1

110

n

i

ii

n

i

n

i

ii

n

i

n

i

ii

n

i

ii

n

i

n

i

n

i

n

i

n

i

xyxaxxaxa

xyxxaxaxa

yxaxana

2. Определим коэффициенты системы нормальных уравнений:

2.1. Представим таблицу исходных данных для удобства расчетов сле-

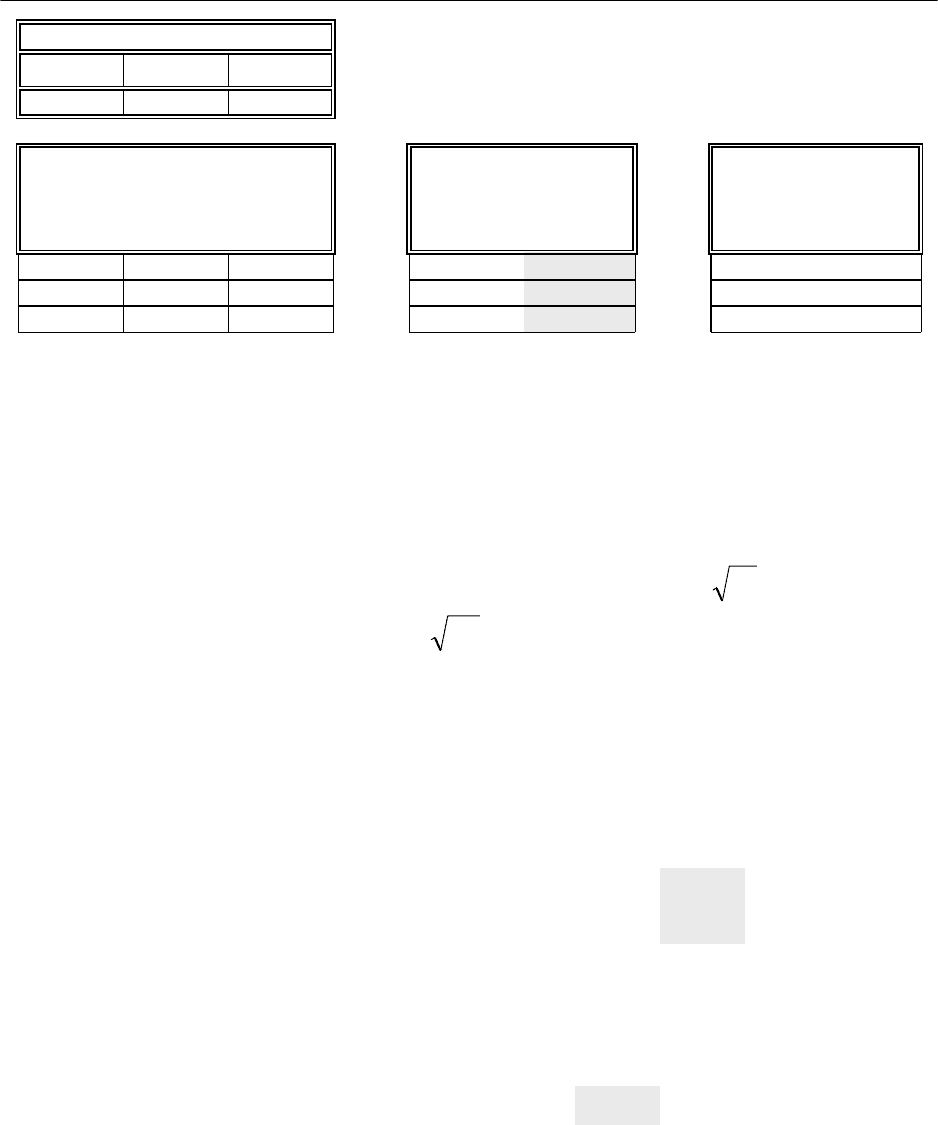
дующим образом (рис. 5.2) и дополним ее еще пятью расчетными столбцами:

Корень из , Корень из , Корень из

1

x

2

x

21

xx

⋅

, ·(корень из ), ·(корень из

).

y

1

x

y

2

x

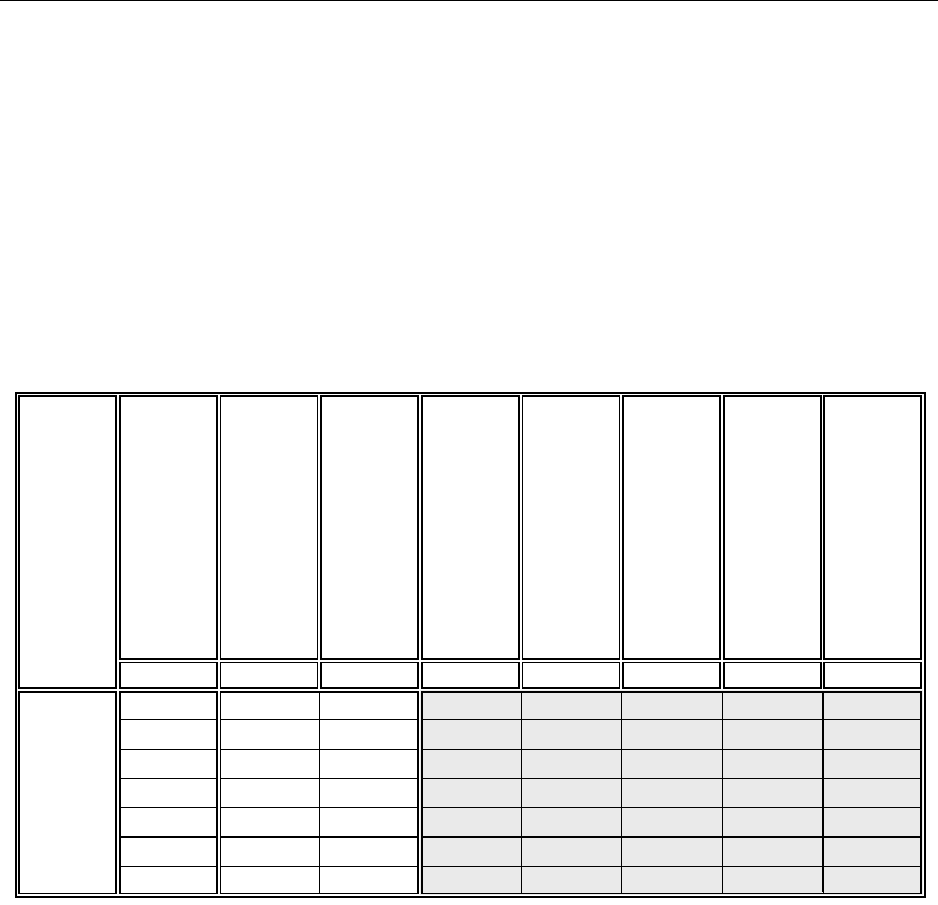
2.2. В верхнюю ячейку столбца 4 введем формулу и автоматически за-

полним весь столбец (протягиванием ячейки с формулой на область заполне-

ния).

=КОРЕНЬ(«верхняя ячейка столбца »)

1

x

Вызов функции: MS Excel – Вставка – Функция… – Математические

Тема лабораторной работы: Нелинейные регрессионные модели: идентификация, прогноз, графическое представление.

3из9

Лектор: к.ф.-м.н., доцент Иванов Андрей Николаевич

Кафедра «Прикладная математика» ДВГУПС

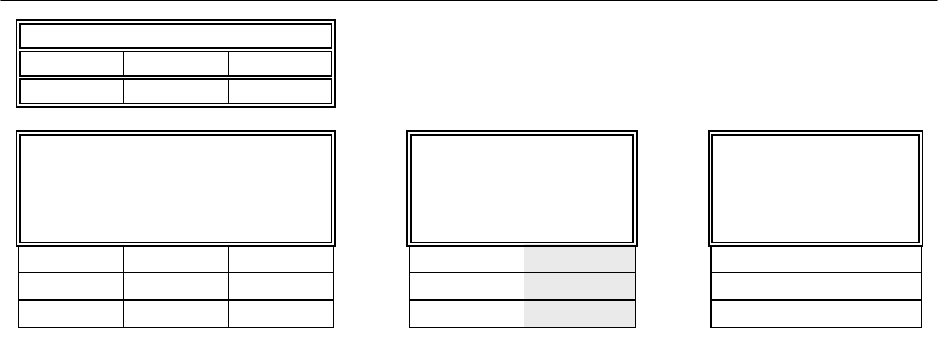
2.3. В верхнюю ячейку столбца 5 введем формулу и автоматически за-

полним весь столбец (протягиванием ячейки с формулой на область заполне-

ния):

=КОРЕНЬ(«верхняя ячейка столбца »)

2

x

2.4. В верхнюю ячейку столбца 6 введем формулу и автоматически за-

полним весь столбец (протягиванием ячейки с формулой на область заполне-

ния):

=КОРЕНЬ(«верхняя ячейка столбца »*«верхняя ячейка

столбца »)

1

x

2

x

ВРП на душу

населения (у), тыс. руб.

Инвестиции в основной

капитал (х

1

), тыс. руб.

Уровень безработицы

(х

2

), %

Корень из x

1

Корень из x

2

Корень из x

1

·x

2

y·(корень из x

1

)

y·(корень из x

2

)

12345678

1 218,12 36,49 0,6

6,04 0,77 4,68 1317,60 168,96

2 78,68 18,55 1

4,31 1,00 4,31 338,87 78,68

3 88,13 14 1,8

3,74 1,34 5,02 329,75 118,24

4 299,4 83,93 2,1

9,16 1,45 13,28 2742,90 433,87

5 78,9 15,52 1,6

3,94 1,26 4,98 310,83 99,80

6 82,01 8,92 1

2,99 1,00 2,99 244,93 82,01

7 71,33 10,78 0,7

3,28 0,84 2,75 234,20 59,68

№

пп

Рис. 5.2

2.5. В верхнюю ячейку столбца 7 введем формулу и автоматически за-

полним весь столбец (протягиванием ячейки с формулой на область заполне-

ния):

=«верхняя ячейка столбца »*«верхняя ячейка столбца «корень

из »»

y

1

x

2.6. В верхнюю ячейку столбца 8 введем формулу и автоматически за-

полним весь столбец (протягиванием ячейки с формулой на область заполне-

ния):

=«верхняя ячейка столбца »*«верхняя ячейка столбца «корень из

»»

y

2

x

Тема лабораторной работы: Нелинейные регрессионные модели: идентификация, прогноз, графическое представление.

4из9

Лектор: к.ф.-м.н., доцент Иванов Андрей Николаевич

Кафедра «Прикладная математика» ДВГУПС

2.7. Просуммируем значения всех столбцов с помощью функции СУММ,

а результат суммирования запишем под столбцом с соответствующими дан-

ными (рис. 5.3).

2.8. Записываем систему нормальных уравнений с найденными коэффи-

циентами:

⎪

⎩

⎪

⎨

⎧

=++

.24,10418,83867,7

,09,55193819,18846,33

,57,91667,746,337

210

aaa

ВРП на душу

населения (у), тыс. руб.

Инвестиции в основной

капитал (х

1

), тыс. руб.

Уровень безработицы

(х

2

), %

Корень из x

1

Корень из x

2

Корень из x

1

·x

2

y·(корень из x

1

)

y·(корень из x

2

)

12345678

1 218,12 36,49 0,6

6,04 0,77 4,68 1317,60 168,96

2 78,68 18,55 1

4,31 1,00 4,31 338,87 78,68

3 88,13 14 1,8

3,74 1,34 5,02 329,75 118,24

4 299,4 83,93 2,1

9,16 1,45 13,28 2742,90 433,87

5 78,9 15,52 1,6

3,94 1,26 4,98 310,83 99,80

6 82,01 8,92 1

2,99 1,00 2,99 244,93 82,01

7 71,33 10,78 0,7

3,28 0,84 2,75 234,20 59,68

Сумма 916,57 188,19 8,80 33,46 7,67 38,00 5519,09 1041,24

№

пп

Рис. 5.3

3. Решаем систему нормальных уравнений с помощью надстройки

Поиск

решения...

3.1. Составим исходную табличную модель для решения системы линей-

ных алгебраических уравнений с помощью надстройки

Поиск решения...

(рис. 5.4).

Тема лабораторной работы: Нелинейные регрессионные модели: идентификация, прогноз, графическое представление.

5из9

Лектор: к.ф.-м.н., доцент Иванов Андрей Николаевич

Кафедра «Прикладная математика» ДВГУПС

а

0

а

1

а

2

012

7 33,46 7,67 48,8 = 916,57

33,46 188,19 38 264,19 = 5519,09

7,67 38 8,8 55,6 = 1041,24

Значения левых

частей уравнений

Свободные члены

исходной системы

Переменные

Матрица коэффициентов

исходной системы

Рис. 5.4

3.2. В блок «Переменные» в первую строку записываем переменные сис-

темы алгебраических уравнений.

3.3. В блок «Переменные» во вторую строку записываем произвольные

числовые значения (удобнее поставить в качестве числовых значений номера

переменных) – в дальнейшем, после выполнения команды Поиск решения...,

в этих ячейках получим исходные решения системы.

3.4. В блок «Матрица коэффициентов исходной системы» записываем со-

ответствующую матрицу коэффициентов при переменных , , .

0

a

1

a

2

a

3.5. В блок «Значения левых частей уравнений» в верхнюю ячейку вво-

дим формулу:

=СУММПРОИЗВ(«фиксированный диапазон строки значений пере-

менных , , »;«диапазон первой строки матрицы коэффициентов

исходной системы»)

0

a

1

a

2

a

3.6. Автоматически заполняем весь столбец «Значения левых частей

уравнений».

3.7. В блок «Свободные члены исходной системы» в столбец записываем

значения правой части исходной системы.

3.8. Вызываем надстройку

Поиск решения… и заполняем форму:

Вызов Поиск решения...:

MS Excel – Сервис – Поиск решения…

Установить целевую ячейку – ничего не ставить;

Равной – максимальному значению;

Изменяя ячейки – диапазон строки значений переменных;

Ограничения – диапазон «Значения левых частей уравнений» = диа-

пазон «Свободные члены исходной системы»;

нажать

Выполнить.

3.8.1. Заполнить форму

Результаты поиска решений:

поставить опцию

Сохранить найденное решение;

нажать

ОК.

Результат выполнения команды Поиск решения… будет следующий

(рис. 5.5).

Тема лабораторной работы: Нелинейные регрессионные модели: идентификация, прогноз, графическое представление.

6из9

Лектор: к.ф.-м.н., доцент Иванов Андрей Николаевич

Кафедра «Прикладная математика» ДВГУПС

а

0

а

1

а

2

-17,337 42,687 -50,896

7 33,46 7,67 916,57 = 916,57

33,46 188,19 38 5519,09 = 5519,09

7,67 38 8,8 1041,24 = 1041,24

Переменные

Значения левых

частей уравнений

Свободные члены

исходной системы

Матрица коэффициентов

исходной системы

Рис. 5.5

3.9. Изменить формат ячеек с полученным решением (строка значений

переменных) так, чтобы было три знака после запятой.

4. Записываем уравнение двухфакторной нелинейной регрессии.

Уравнение нелинейной регрессии:

.x,

x, + ,y =

2

1

794895745107250

16868680160514268337145247717

−

−−

5. Осуществим точечный прогноз при средних значениях обоих факторов.

5.1. Вычислим средние значения факторов и с помощью функции

MS Excel

СРЗНАЧ

1

x

2

x

=СРЗНАЧ(«диапазон значений столбца »)

1

x

=СРЗНАЧ(«диапазон значений столбца »)

2

x

26,88

1,26

среднее значение фактора x

1

=

среднее значение фактора x

2

=

5.2. Подставив найденные средние значения факторов и в уравне-

ние нелинейной регрессии, получим точечный прогноз ( -прогнозное)

1

x

2

x

y

146,9

y-прогнозное =

6. Построим поверхность двухфакторной нелинейной регрессии.

6.1. Составим вспомогательную таблицу модельных значений при всех

исходных значениях факторов (рис. 5.6).

Иванов А.Н. Построение эконометрических моделей и прогнозирование в MS Excel: сборник лабораторных работ

Подождите немного. Документ загружается.