Иванов А.Н. Построение эконометрических моделей и прогнозирование в MS Excel: сборник лабораторных работ
Подождите немного. Документ загружается.

Тема лабораторной работы: Матричная алгебра в идентификации модели множественной линейной регрессии.
4из17
Анализ качества модели множественной линейной регрессии.
Интервальное оценивание параметров уравнения множественной линейной регрессии.
Лектор: к.ф.-м.н., доцент Иванов Андрей Николаевич
Кафедра «Прикладная математика» ДВГУПС
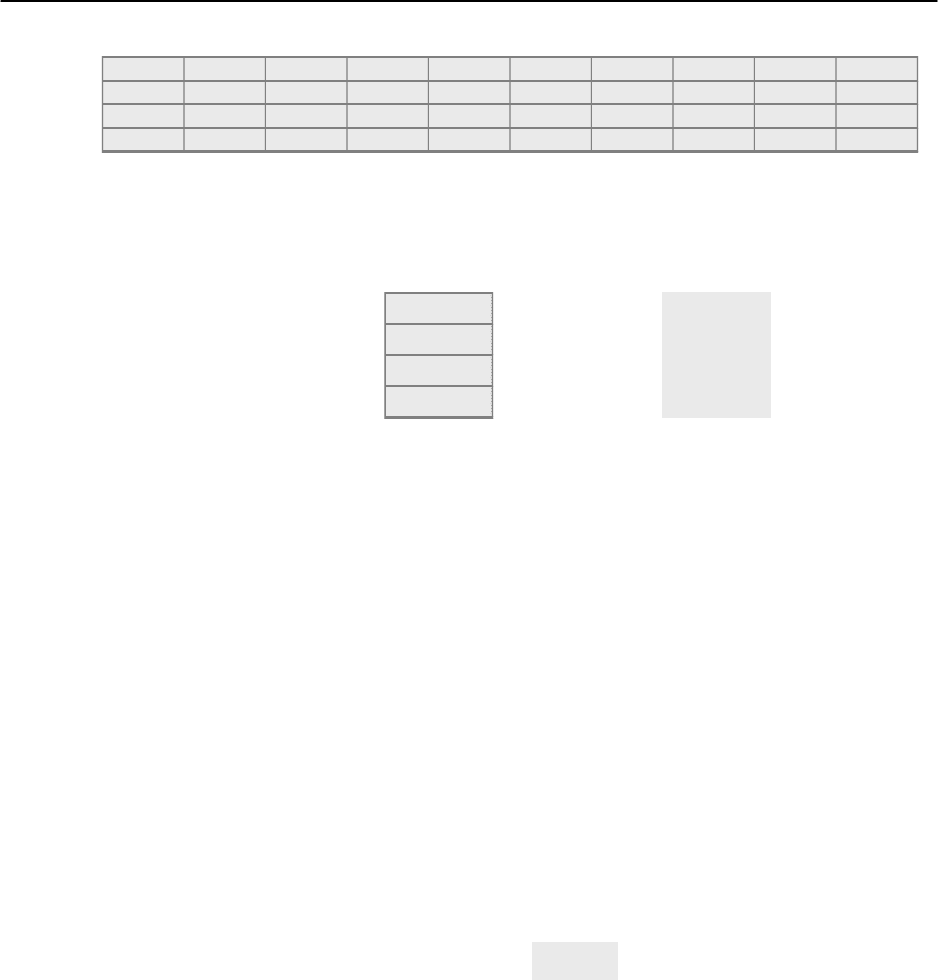
-1,9294 -2,4987 0,5329 1,2514 0,5609 1,567 0,3529 0,0438 0,3851 0,7341
(
X
T
X
)
-1
X
T
=
-0,0944 -0,0293 -0,0306 0,0722 0,0594 -0,0337 -0,0176 -0,0517 0,0326 0,0931
0,0183 0,0279 -0,0022 -0,0138 -0,0141 -0,0119 -0,0011 0,0058 0,0009 -0,0099
0,1402 0,0211 0,0085 -0,061 0,0413 0,0003 0,0028 -0,0022 -0,0827 -0,0684
2.3.5. Находим матрицу .
()
YXXXa
TT
1−
=
9,8367
a
0
=
9,8367
a
=
(
X
T
X
)
-1
X
T
Y
=
0,9861
a
1
=
0,9861
0,1498
a
2
=
0,1498
-1,1882
a
3
=
-1,1882
Замечание 4.2. Для выделения нужного числа из матрицы, используем
функцию ИНДЕКС в MS Excel.
Замечание 4.3. Найденные значения параметров модели , , , –
есть оценки данных параметров, которые обозначаются с крышкой.
0
a
1
a
2
a
3
a
Вывод. Трехфакторное уравнение регрессии имеет вид
321
1882,114981,098607,083673,9 xxxy −++=
.
3. Для нахождения общей, факторной и остаточной дисперсии дополним
таблицу исходных данных еще четырьмя столбцами: y-оценка, общей, фак-
торной и остаточной суммами квадратов (рис. 4.4).
3.1. Находим среднее значение , используя функцию СРЗНАЧ.
y
Вызов функции: MS Excel – Вставка – Функция… – Статистические
y-среднее = 23,9
3.2. В столбец « -оценка» вставляем формулу и автоматически заполня-
ем столбцы (протягиванием ячейки с формулой на область заполнения):
y
=«фиксированная ячейка оценки параметра »+«фиксированная
ячейка оценки параметра »* +«фиксированная ячейка оценки пара-
метра »* +«фиксированная ячейка оценки параметра »*
0
a
1
a
1
x
2
a
2
x
3
a
3
x
3.3. В столбец «общая сумма квадратов» вставляем формулу и автомати-
чески заполняем столбец (протягиванием ячейки с формулой на область за-
полнения):
=СТЕПЕНЬ(y – «y-среднее»;2)
Тема лабораторной работы: Матричная алгебра в идентификации модели множественной линейной регрессии.
5из17
Анализ качества модели множественной линейной регрессии.
Интервальное оценивание параметров уравнения множественной линейной регрессии.
Лектор: к.ф.-м.н., доцент Иванов Андрей Николаевич
Кафедра «Прикладная математика» ДВГУПС
3.4. В столбец «факторная сумма квадратов» вставляем формулу и авто-
матически заполняем столбец (протягиванием ячейки с формулой на область
заполнения):
=СТЕПЕНЬ(«y-оценка» - «y-среднее»;2)
№
п/п
Цена
(y)
Затраты
(удельные) (x
1
)
Постоянные
затраты (x
2
)
Объем (x
3
), шт.
y-оценка
Общая сумма
квадратов
Факторная сум-
ма квадратов
Остаточная сум-
ма квадратов
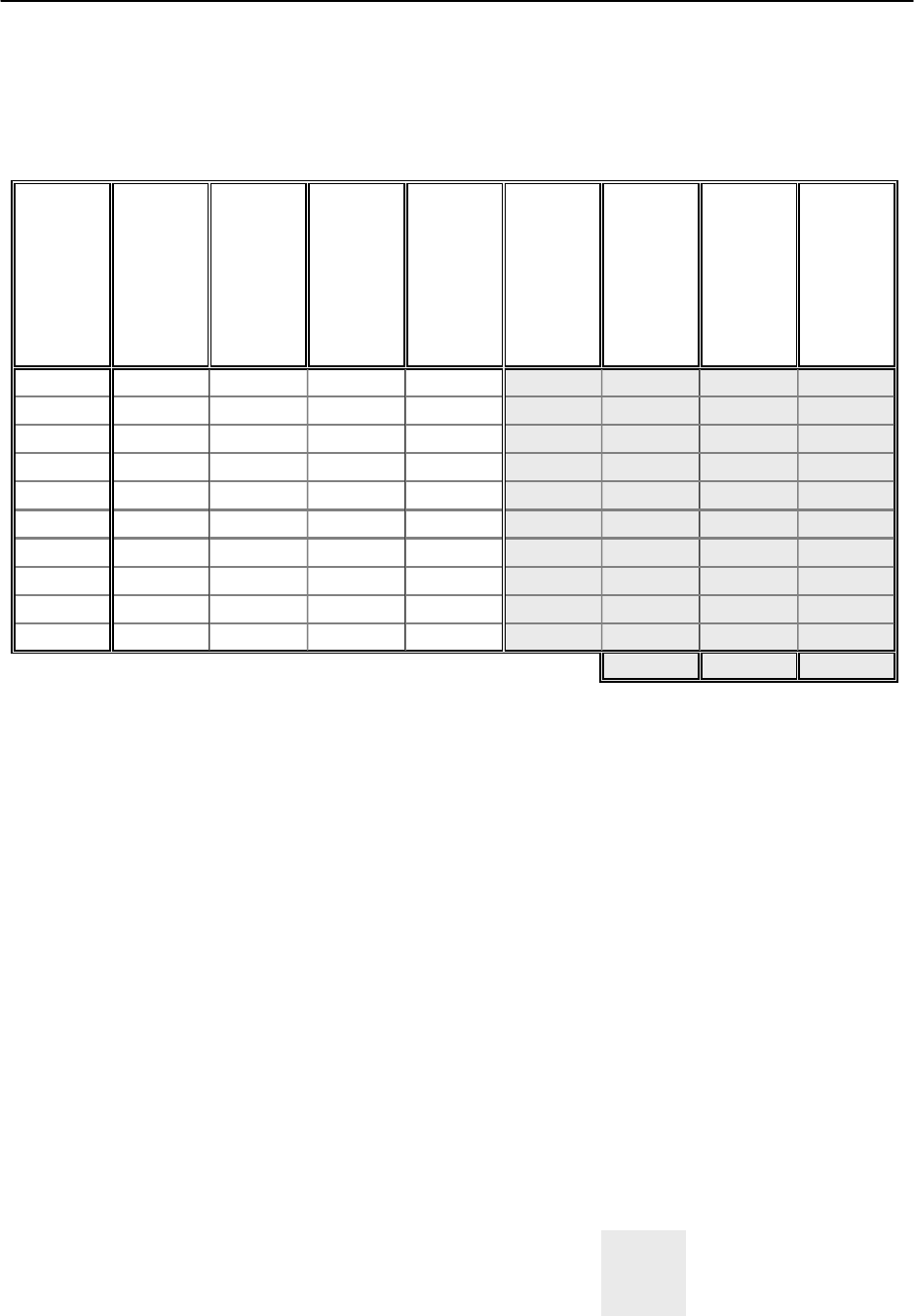
1 20 10 100 12,00 20,42 15,21 12,113 0,1761
2 30 12 120 8,00 30,141 37,21 38,949 0,0199
3 21 7 90 7,50 21,31 8,41 6,7061 0,0963
4 25 11 94 7,90 25,379 1,21 2,1863 0,1433
5 23 14 91 13,00 21,827 0,81 4,2955 1,3749
6 18 5 80 7,00 18,434 34,81 29,874 0,1886
7 22 8 93 7,70 22,508 3,61 1,937 0,2583
8 24 6 95 6,00 22,856 0,01 1,0905 1,3094
9 29 9 103 5,00 28,201 26,01 18,495 0,639
10 27 13 101 8,30 27,924 9,61 16,194 0,854
136,9 131,84 5,0599
Рис. 4.4
3.5. В столбец «остаточная сумма квадратов» вставляем формулу и авто-
матически заполняем столбец (протягиванием ячейки с формулой на область
заполнения):
=СТЕПЕНЬ(y – «y-оценка»;2)
3.6. Суммированием по трем столбцам находим соответственно общую,
факторную и остаточную суммы квадратов. Используем функцию СУММ.
3.7. Определяем число степеней свободы общей, факторной и остаточной
сумм квадратов соответственно.
Число степеней свободы общей суммы квадратов: .
91101 =−=−n
Число степеней свободы факторной суммы квадратов:
3=
k
.
Число степеней свободы остаточной суммы квадратов:
613101 =−−=−−
k
n
.
3.7. Дисперсии находим делением соответствующих сумм квадратов на
соответствующие им числа степеней свободы:
15,21
43,95
0,843
факторная дисперсия =
остаточная дисперсия =
общая дисперсия =
Тема лабораторной работы: Матричная алгебра в идентификации модели множественной линейной регрессии.
6из17
Анализ качества модели множественной линейной регрессии.
Интервальное оценивание параметров уравнения множественной линейной регрессии.
Лектор: к.ф.-м.н., доцент Иванов Андрей Николаевич
Кафедра «Прикладная математика» ДВГУПС
4. Вычисляем коэффициент детерминации по формуле:
=1 – «остаточная сумма квадратов»/«общая сумма квадратов»
0,963
коэффициент детерминации =
5. Для нахождения средней ошибки аппроксимации припишем еще один
столбец к расчетной таблице: «аппроксимация» (рис. 4.5).
№
п/п
Цена
(y)
Затраты
(удельные) (x
1
)
Постоянные
затраты (x
2
)
Объем (x
3
), шт.
y-оценка
Общая сумма
квадратов
Факторная сум-
ма квадратов
Остаточная сум-
ма квадратов
Аппроксимация
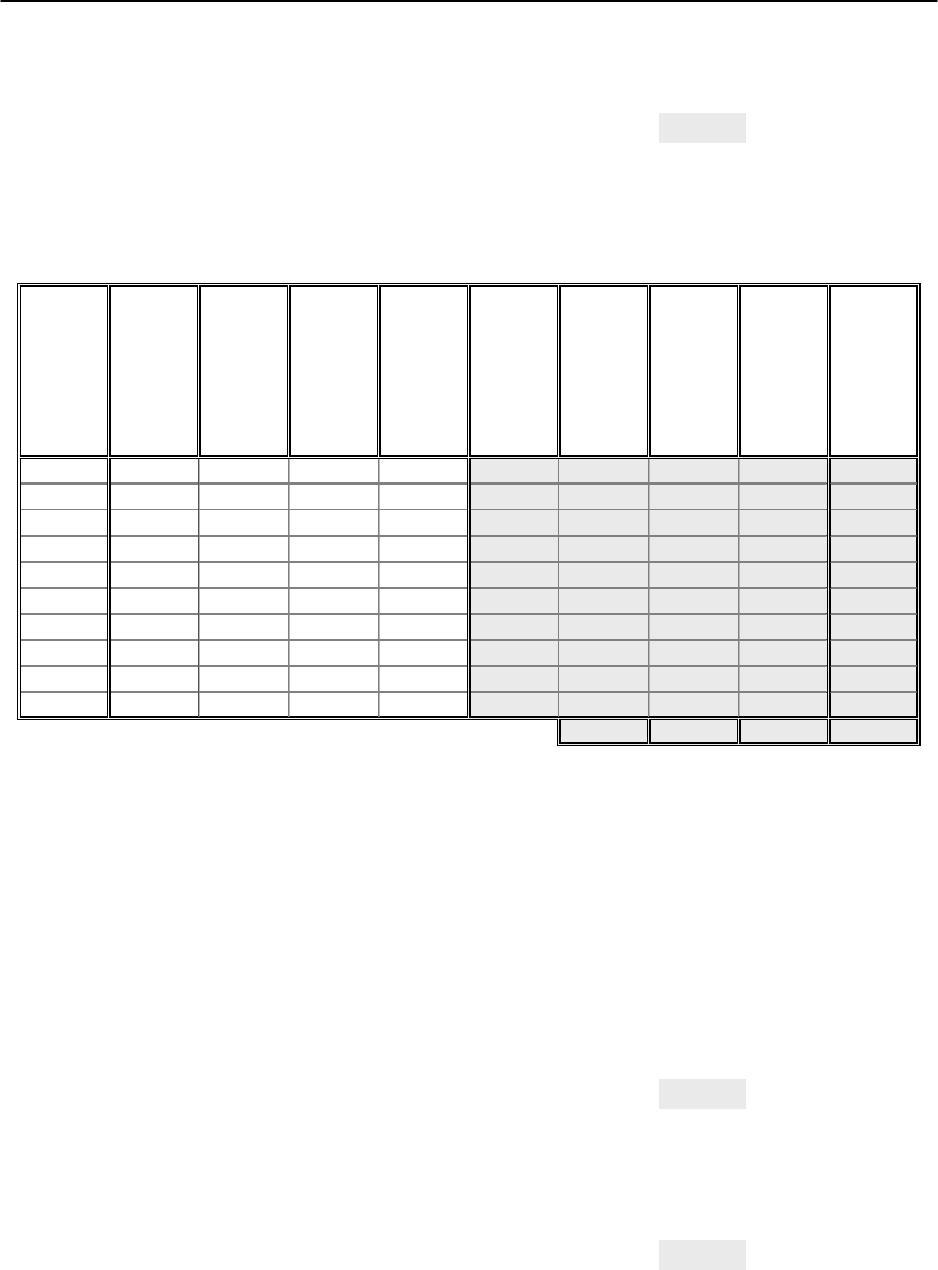
1 20 10 100 12,00 20,42 15,21 12,113 0,1761 0,021
2 30 12 120 8,00 30,141 37,21 38,949 0,0199 0,0047
3 21 7 90 7,50 21,31 8,41 6,7061 0,0963 0,0148
4 25 11 94 7,90 25,379 1,21 2,1863 0,1433 0,0151
5 23 14 91 13,00 21,827 0,81 4,2955 1,3749 0,051
6 18 5 80 7,00 18,434 34,81 29,874 0,1886 0,0241
7 22 8 93 7,70 22,508 3,61 1,937 0,2583 0,0231
8 24 6 95 6,00 22,856 0,01 1,0905 1,3094 0,0477
9 29 9 103 5,00 28,201 26,01 18,495 0,639 0,0276
10 27 13 101 8,30 27,924 9,61 16,194 0,854 0,0342
136,9 131,84 5,0599 0,2633
Рис. 4.5
5.1. В столбец «аппроксимация» вставляем формулу Excel:
=ABS((y – «y-оценка»)/y)
5.2. Суммируем все значения столбца «аппроксимация», используя функ-
цию СУММ.
5.3. Вычисляем среднюю ошибку аппроксимации по формуле:
=1/n*«сумма модулей столбца аппроксимация»*100%
(числовой формат ячейки при этом должен быть Процентный)
2,63%
средняя ошибка аппроксимации =
6. Вычисляем стандартную ошибку регрессии по формуле:
=КОРЕНЬ(1/(n-k-1)*«остаточная сумма квадратов»)
0,918
стандартная ошибка регрессии =
7. Вычислим стандартные ошибки параметров регрессии по формуле:

Тема лабораторной работы: Матричная алгебра в идентификации модели множественной линейной регрессии.
7из17
Анализ качества модели множественной линейной регрессии.
Интервальное оценивание параметров уравнения множественной линейной регрессии.
Лектор: к.ф.-м.н., доцент Иванов Андрей Николаевич
Кафедра «Прикладная математика» ДВГУПС
=КОРЕНЬ(1/(n-k-1)*«остаточная сумма квадра-
тов»*ИНДЕКС(«диапазон матрицы »;i+1;i+1))
(
1−
XX
T
)
i – номер коэффициента регрессии.
3,604
0,168
0,039
0,177
стандартная ошибка а
1
=
стандартная ошибка а
2
=
стандартная ошибка а
3
=
стандартная ошибка а
0
=
8. Проверим общее качество модели.
8.1. Проверяем гипотезы:
.:
,:
остатфактор1
остатфактор0
DDH
DDH
=
/
=
8.2. Строим статистику:
F =«факторная дисперсия»/«остаточная дисперсия»
F = 52,11
8.3. Находим квантиль распределения Фишера – Снедекора с
3=
k
и
613101 =−−=−−
k
n
степенями свободы при уровне значимости, равном
0,05. Используем функцию FРАСПОБР.
Вызов функции: MS Excel – Вставка – Функция… – Статистические
=FРАСПОБР(«уровень значимости»;k;n-k-1)
4,757
F-квантиль =
8.4. Делаем вывод о принятии гипотезы:
=ЕСЛИ(F>=«F-квантиль»;"отвергается и принимается альтерна-
тивная гипотеза, следовательно, уравнение парной линейной регрессии
значимо в целом.";"принимается.")
Гипотеза H
0
: D
ф
акт о
р
= D
остат
отвергается и принимается альтернативная
гипотеза, следовательно, уравнение парной
линейной регрессии значимо в целом.
9. Проверим статистическую значимость коэффициентов уравнения рег-
рессии.
9.1. Проверяем гипотезы:

Тема лабораторной работы: Матричная алгебра в идентификации модели множественной линейной регрессии.
8из17
Анализ качества модели множественной линейной регрессии.
Интервальное оценивание параметров уравнения множественной линейной регрессии.
Лектор: к.ф.-м.н., доцент Иванов Андрей Николаевич
Кафедра «Прикладная математика» ДВГУПС
.0:
,0:
11
10
=
/
=
aH
aH
9.2. Строим статистику:
1
t =ABS(«параметр регрессии »/ «стандартная ошибка »)
1
a
1
a
t
1
= 5,887
9.3. Находим квантиль распределения Стьюдента с
613101 =−−=−−
k
n
степенями свободы при уровне значимости, равном
0,05. Используем функцию СТЬЮДРАСПОБР.
Вызов функции: MS Excel – Вставка – Функция… – Статистические
=СТЬЮДРАСПОБР(«уровень значимости»;n-k-1)
2,447t-квантиль =
9.4. Делаем вывод о принятии гипотезы:
=ЕСЛИ( >=«t-квантиль»;"отвергается и принимается альтерна-
тивная гипотеза, следовательно, коэффициент уравнения множествен-
ной линейной регрессии статистически значим, то есть 1-й фактор
оказывает существенное влияние на модель.";"принимается, это озна-
чает, что фактор не связан линейно с зависимой переменной y и его
можно исключить из набора факторов.")
1
t
1
a
1
x
отвергается и принимается
альтернативная гипотеза, следовательно,
коэффициент уравнения множественной
линейной регрессии а1 статистически
значим, то есть 1-й фактор оказывает
существенное влияние на модель.
Гипотеза H
0
: a
1
= 0
9.5. По аналогии с предыдущим, проверяем статистическую значимость
коэффициента уравнения регрессии .
2
a
9.6. Проверяем гипотезы:
.0:
,0:
21
20
=
/
=
aH
aH
9.7. Строим статистику:
t
2
=
3,86
9.8. Делаем вывод о принятии гипотезы:

Тема лабораторной работы: Матричная алгебра в идентификации модели множественной линейной регрессии.
9из17
Анализ качества модели множественной линейной регрессии.
Интервальное оценивание параметров уравнения множественной линейной регрессии.
Лектор: к.ф.-м.н., доцент Иванов Андрей Николаевич
Кафедра «Прикладная математика» ДВГУПС
отвергается и принимается
альтернативная гипотеза, следовательно,
коэффициент уравнения множественной
линейной регрессии а2 статистически
значим, то есть 2-й фактор оказывает
существенное влияние на модель.
Гипотеза H
0
: a
2
= 0
9.9. Проверяем статистическую значимость коэффициента уравнения рег-
рессии .
3
a
9.10. Проверяем гипотезы:
.0:
,0:
31
30
=
/
=
aH
aH
9.11. Строим статистику:
t
3
= 6,715
9.12. Делаем вывод о принятии гипотезы:
Гипотеза H
0
: a
3
= 0
отвергается и принимается
альтернативная гипотеза, следовательно,
коэффициент уравнения множественной
линейной регрессии а3 статистически
значим, то есть 3-й фактор оказывает
существенное влияние на модель.
Анализ качества, построенной регрессионной модели позволяет сделать
следующие выводы:
– модель качественна в целом при уровне значимости 0,05;
– все факторы, включенные в модель, существенны при уровне значимо-
сти 0,05;
– средняя ошибка аппроксимации не превышает 5 %, что говорит об аде-
кватности построенной модели, то есть о высоком качестве;
– коэффициент детерминации близок к единице, что говорит о тесной ли-
нейной связи всех факторов с зависимой переменной ;
y
– прогноз, получаемый по данной модели, будет высокой точности, то
есть ошибка осуществления неверного прогноза будет мала.
10. Произведем интервальное оценивание параметров трёхфакторной
регрессионной модели.
Доверительный интервал для параметра регрессионной модели есть
интервал вида:
i
a

Тема лабораторной работы: Матричная алгебра в идентификации модели множественной линейной регрессии.
10из17
Анализ качества модели множественной линейной регрессии.
Интервальное оценивание параметров уравнения множественной линейной регрессии.
Лектор: к.ф.-м.н., доцент Иванов Андрей Николаевич
Кафедра «Прикладная математика» ДВГУПС
ii
a
kn
iia
kn
i
taata
ˆ
1,
2
ˆ
1,
2
ˆˆˆˆ
σ
σ
αα
−−−−
+≤≤−
.
=«оценка i-го параметра уравнения регрессии» - «t-квантиль»* «стан-
дартная ошибка i-го параметра»
1,0187
<=а
0
<=
18,655
0,5762
<=а
1
<=
1,3959
0,0548
<=а
2
<=
0,2448
-1,6212
<=а
3
<=
-0,7552
11. Осуществим точечный прогноз по построенной модели, подставив
значения факторов в уравнение регрессии и определив значение зависимой
переменной :
y
26,014y-прогнозное =
К
К
К
о
о
о
н
н
н
т
т
т
р
р
р
о
о
о
л
л
л
ь
ь
ь
н
н
н
ы
ы
ы
е
е
е
в
в
в
о
о
о
п
п
п
р
р
р
о
о
о
с
с
с
ы
ы
ы
и
и
и
у
у
у
п
п
п
р
р
р
а
а
а
ж
ж
ж
н
н
н
е
е
е
н
н
н
и
и
и
я
я
я
1. Для чего необходима выполнимость условия
(
)
0det ≠XX
T
?
2. Что означает построить доверительный интервал для параметра регрес-
сионной модели?
3. Для чего в анализе качества модели применяется F-критерий и t-
критерий?
4. С помощью какой функции MS Excel вычисляется квантиль распреде-
ления Фишера – Снедекора?
5. Если один из факторов эконометрической модели статистически незна-
чим, можно ли его исключить из модели? Если оставить или удалить один
незначимый фактор, то к чему это приведет?
6. Как осуществить точечный прогноз по уравнению множественной ли-
нейной регрессии?
7. Можно ли делать прогноз по некачественной эконометрической моде-
ли?
8. Какая основная цель построения трёхфакторной регрессионной моде-
ли?
9. Что вычисляет функция MS Excel – ABS?
10. Как записать гипотезу об общей значимости модели множественной
линейной регрессии?
Тема лабораторной работы: Матричная алгебра в идентификации модели множественной линейной регрессии.
11из17
Анализ качества модели множественной линейной регрессии.
Интервальное оценивание параметров уравнения множественной линейной регрессии.
Лектор: к.ф.-м.н., доцент Иванов Андрей Николаевич
Кафедра «Прикладная математика» ДВГУПС
В
В
В
а
а
а
р
р
р
и
и
и
а
а
а
н
н
н
т
т
т
ы
ы
ы
и
и
и
н
н
н
д
д
д
и
и
и
в
в
в
и
и
и
д
д
д
у
у
у
а
а
а
л
л
л
ь
ь
ь
н
н
н
ы
ы
ы
х
х
х
з
з
з
а
а
а
д
д
д
а
а
а
н
н
н
и
и
и
й
й
й
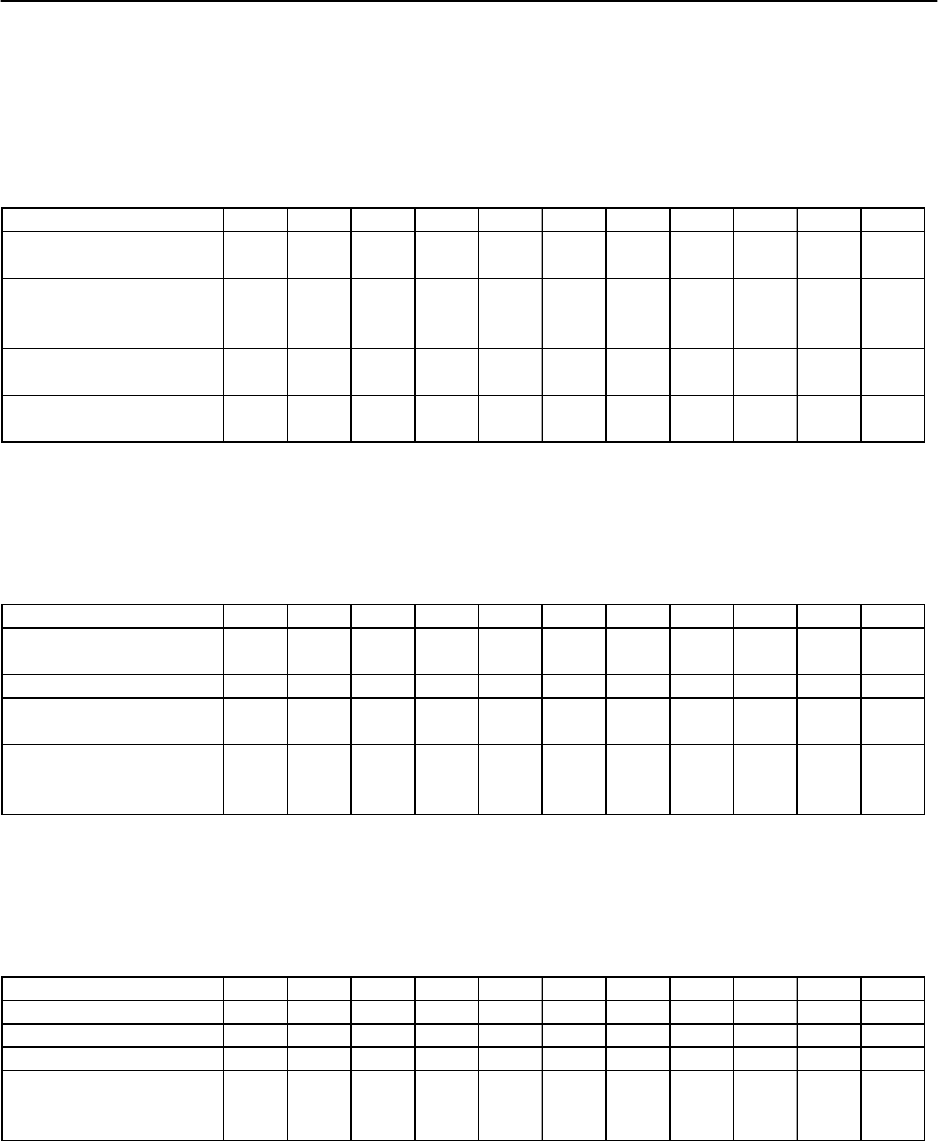
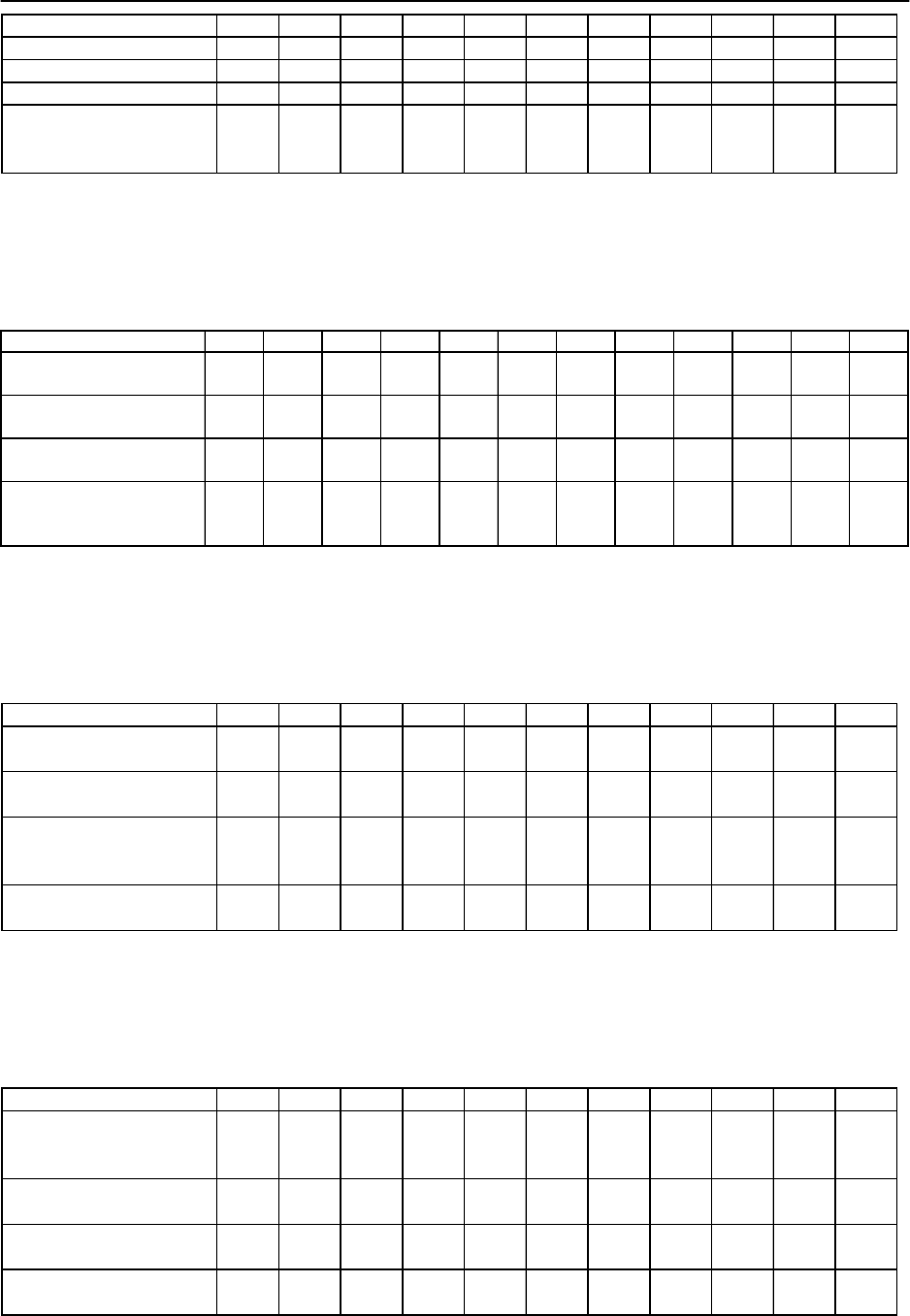
1. Данные Хабаровска
за период с 1996 по 2005 годы. Осуществить то-
чечный прогноз при значениях факторов равных 101 % от их средних значе-
ний.
1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005
4527 62051566 2426 3286
64196284
18 19,5 21
887,9 943,5 1174 1323
15,5161617
6825 6959 6734 66006632 6952 6823 6776
401 414,3
22
432,2
8945 10684
23 23,5 24,5
6202
230 277 295 380
Год
Потребление молока в
месяц (y), л.
Среднедушевой доход
населения
в месяц (x
1
), руб.
Произв-во молока
в месяц (x
2
), т.
Средняя цена
за литр (x
3
), руб.
139,6 156,7 156,7 194,5
2. Имеются данные динамики объема продаж товара на Дальнем Востоке
за 11 лет. Осуществить точечный прогноз при значениях факторов равных
102 % от их средних значений.
1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005
25 27 29 31 34 35 35 36 37 39 40
829613
8945 10684
Кол-во потенциальных
покупателей (x
3
), чел.
887,9 943,5 1174 1323 1566
886524
2426 3286
Год
Объем продаж
товара (y), руб.
856266 854265 822369 836957 812547
3286
844562 856927 869823
10684
896364
Цена (x
1
), руб.
Средняя зарплата
продавцов (x
2
), руб.
888 944 1174 1323 1566 2426 4527 6205 8945
4527 6205
3. Имеются данные структуры внешней торговли Дальнего Востока за 11
лет. Осуществить точечный прогноз при значениях факторов равных 103 %
от их средних значений.
1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005
2951 3326 3594 3826 4239 4712 4962 5263 5887 7610 9495
1569 1836 2223 2589 2864 3029 3326 3754 4123 4622 5102
1382 1490 1371 1237 1375 1683 1636 1509 1764 2988 4393
290 315237 254 261 283200 60
Год
Оборот (y), млн дол.
Иностр. инвестиции
(x
3
), млн дол.
190
Импорт (x
2
), млн. дол.
Экспорт (x
1
), млн дол.
210 220
4. Имеются основные экономические показатели России за 11 лет. Осу-
ществить точечный прогноз при значениях факторов равных 104 % от их
средних значений.
Тема лабораторной работы: Матричная алгебра в идентификации модели множественной линейной регрессии.
12из17
Анализ качества модели множественной линейной регрессии.
Интервальное оценивание параметров уравнения множественной линейной регрессии.
Лектор: к.ф.-м.н., доцент Иванов Андрей Николаевич
Кафедра «Прикладная математика» ДВГУПС
1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005
212 302 372 324 354 351 426 443 504 489 466
90 87 86 86 91 99 104 112 125 131 140
122 215 286 238 263 252 322 331 379 358 326
290 315237 254 261 283200 60 210 220
ВВП (x
1
), млн дол.
ВРП (x
2
), млн дол.
Иностр. инвестиции
(x
3
), млн дол.
190
Год
ВНП (y), млн дол.
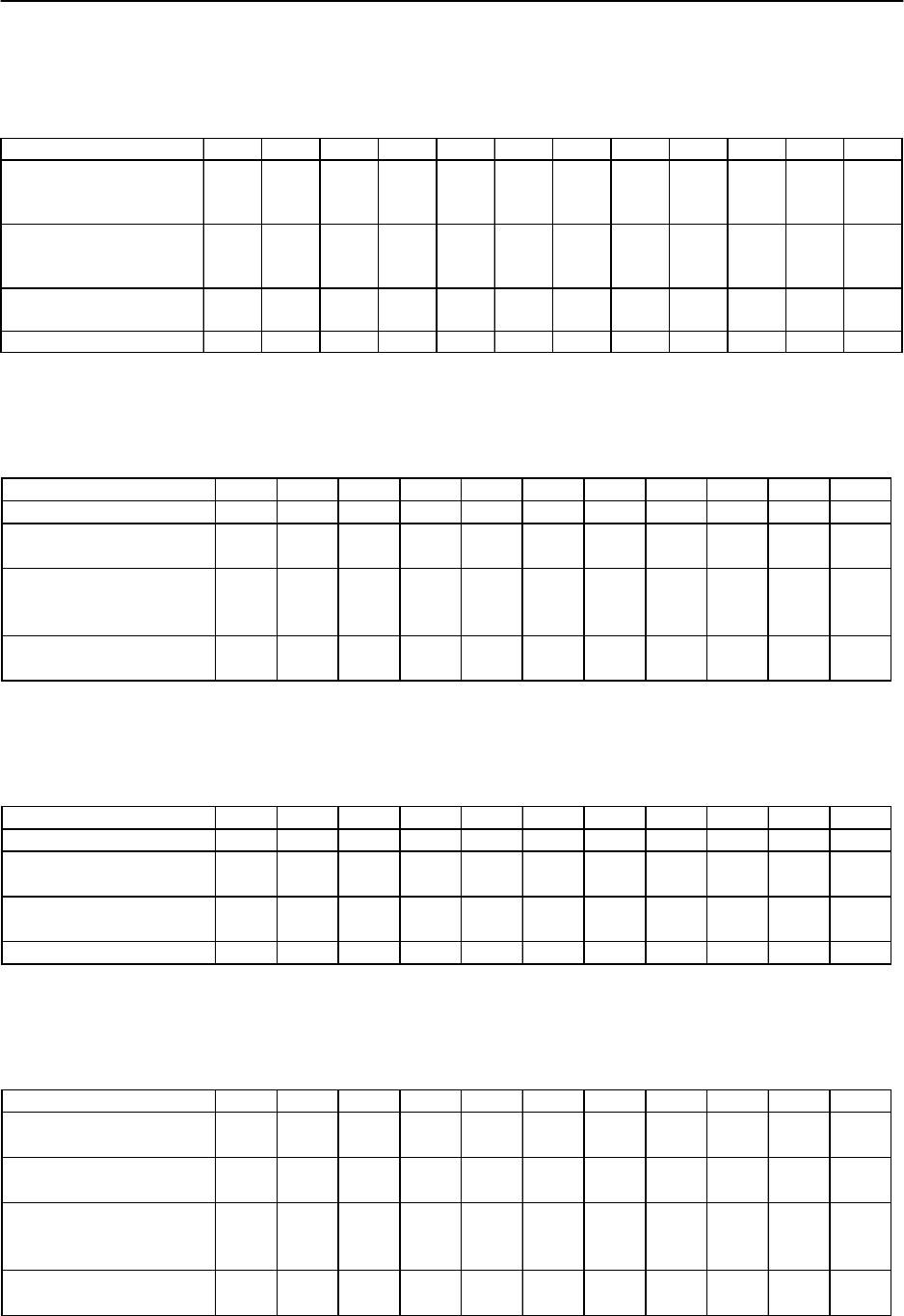
5. Имеются данные потребления электроэнергии в г. Хабаровск за 2005 г.
Осуществить точечный прогноз при значениях факторов равных 105 % от их
средних значений.
янв. фев. март апр. май июнь июль авг. сен. окт. нояб. дек.
0,70,3 0,3 0,3 0,4 0,4 0,4 0,5 0,6
42 40
Тарифная ставка (x
1
),
руб.
0,6
8945 8945
600,1 600,1
8945 8945 8945 8945 8945 8945 8945 8945
50 59
600 600 600 600 600 600 600 600
41 48
Кол-во потребителей
(x
2
), тыс. чел.
Средняя зарплата
потребителей (x
3
), руб.
600
8945 8945
600,1
0,2 0,2
Месяц
Потребление эл-
энергии (y), руб/чел.
60 65 62 55 50 45
6. Имеются данные показателя ВРП по Дальнему Востоку за 11 лет. Осу-
ществить точечный прогноз при значениях факторов равных 106 % от их
средних значений.
1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005
443 504 489 466324 354 351 426
Объем ВРП (y), млн
дол.
212 302 372
142 143 142 145
206 209
Кол-во предп-тий топл.-
энерг. комплекса (x
2
),
ед.
145 142 143 140 139 138 142
209 202 205 204223 220 221 218
200 190 186 187 185 187 189
Год
Кол-во лесопром-ных
предприятий (x
3
), ед.
190 194 193 196
Кол-во с.-х.
предприятий (x
1
), ед.
215
7. Имеются данные динамики безработицы в России за 11 лет. Осущест-
вить точечный прогноз при значениях факторов равных 107 % от их средних
значений.
1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005
205 204 206 209
Кол-во предприятий
(x
1
), ед.
215 223 220 221 218 209 202
315426 351 324 331
106843286 4527 6205 8945
Средняя зарплата (x
3
),
руб.
887,9 943,5 1174
245
ВВП на душу населения
(x
2
)
215 225 224 237 239 248 246 250226 222 232
1323 1566 2426
Год
Кол-во безработных
(y), тыс. чел.
436 504 293 285 264
Тема лабораторной работы: Матричная алгебра в идентификации модели множественной линейной регрессии.
13из17
Анализ качества модели множественной линейной регрессии.
Интервальное оценивание параметров уравнения множественной линейной регрессии.
Лектор: к.ф.-м.н., доцент Иванов Андрей Николаевич
Кафедра «Прикладная математика» ДВГУПС
8. Имеются данные о потреблении мяса говядины в г. Хабаровск за 2004
г. Осуществить точечный прогноз при значениях факторов равных 108 % от
их средних значений.
янв. фев. март апр. май июнь июль авг. сен. окт. нояб. дек.
118 118 119 120 121 123 123 123 124 124 125 125
401
Кол-во потенциальных
потреб. (x
1
), тыс. чел.
401 401396 399 400 398400 401 400 402
170 176
Цена за кг (x
3
), руб.
165 171
3591 3600
178
400
3609
Объем производства
(x
2
), т.
156 163 162 153 149 161
3582
160
Месяц
Объем потребления
мяса говядины (y), тыс.
кг.
3600 3609 3600 3609 3600 36093618 3564
9. Динамика ВРП Дальнего Востока за 11 лет. Осуществить точечный
прогноз при значениях факторов равных 109 % от их средних значений.
1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005
212 302 372 324 354 351 426 443 504 489 466
194 193
204 206
196
121
Кол-во лесопром.
предприятий (x
3
), ед.
200 190 186 187 185 187 189 190
116 119 121 123
209
Предприятия
химической
пром. (x
2
), ед.
110 112 108 105 94 120
218 209 202 205215 223 220 221
Год
ВРП (y), млн дол.
Кол-во с.-х.
предприятий (x
1
), ед.
10. Динамика цены товара за 11 лет. Осуществить точечный прогноз при
значениях факторов равных 110 % от их средних значений.
1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005
60 70 80 90 100 110 120 130 140 150 160
9 10111213141516171819
Амортизация (x
3
), руб.
32 34 36 38 40
9575 80 85
Год
Цена товара (y), руб.
Себестоимость товара
(x
1
), руб.
45 50 9055 60 65 70
Транспортные расходы
(x
2
), руб.
20 22 24 26 28 30
11. Данные по выдаваемым кредитам 11-ти банков. Осуществить точеч-
ный прогноз при значениях факторов равных 111 % от их средних значений.
1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005
192 108
10055
1
45 80
2553
Максимальная сумма
кредита (x
3
), тыс. руб.
60 100 6040 35 50 45
42
Максимальное кол-во
предоставляемых
кредитов (x
2
), ед.
121314
2
Год
Процент по кредиту
(x
1
), руб.
5
54
Объем кредитов (y), шт.
573
237610712
6
