Ибрагимов В.А., Стрельцов С.В. Программа, методические указания и контрольные задания для студентов-заочников. Часть 2
Подождите немного. Документ загружается.


2. Предполагая, что X распределена по нормальному закону и принимая
в качестве оценок его параметров М[X],
[X] выборочное среднее
x
и
выборочное среднеквадратическое отклонение s вычислить теоретическое
частоты интервалов.
3. С помощью критерия согласия Пирсона при уровне значимости
=0,1 проверить, согласуются ли выборочные данные с
гипотезой о нормальном распределении величины Х. Число
степеней свободы принять равным 3.
Задание 8.4.
По заданной корреляционной таблице найти выборочные средние
,y,x
среднеквадратические отклонения s
x
, s
y
, коэффициент
корреляции
xy
и уравнение линейной регрессии Y на X. Вычислить
условные средние
x
y
по данным таблицы и с помощью выборочного
уравнения регрессии и найти наибольшее их отклонение.
1.
У
Х
14 19 24 29 34 n
х
16 2 2 4
18 3 4 7
20 13 6 3 22
22 9 21 13 2 45
24 19 29 9 57
26 8 17 25
n
y
5 28 46 53 28 160
2.
Y
X
19 24 29 34 39 N
x
18 1 2 3
20 2 3 5
22 4 5 2 11
24 7 15 5 1 28
61

26 13 8 2 23
n
y
3 16 33 15 3 70
3.
Y
X
20 25 30 35 40 50 n
x
16 2 3 5
18 3 4 1 8
20 7 20 3 30
22 10 5 3 2 20
24 5 2 7
n
y
5 14 31 8 8 4 70
4.
Y
X
15 20 25 30 35 n
x
18 1 2 3
20 1 2 4 7
22 4 3 9 16
24 2 5 6 13
26 1 7 1 9
28 1 1 2
n
y
2 10 13 23 2 50
5.
Y
X
14 18 22 26 30 34 N
x
17 2 1 3
19 1 3 3 7
21 3 4 8 15
23 3 6 7 16
25 1 5 1 7
62

27 1 1 2
n
y
3 7 10 15 13 2 50
6.
Y
X
10 14 18 22 26 30 n
x
15 3 4 7
25 2 6 8
35 3 50 4 5 57
45 2 8 6 16
55 3 3 7 2 12
n
y
3 6 11 61 17 2 100
7.
Y
X
8 14 20 26 32 38 N
x
10 5 1 6
20 6 2 8
30 5 40 5 50
40 2 8 7 17
50 4 7 8 19
n
y
5 7 9 52 19 8 100
8.
Y
X
10 20 30 40 50 60 n
x
18 2 4 6
26 3 7 10
34 1 48 10 2 61
42 2 7 5 14
50 1 2 2 5
58 2 2 4
63

n
y
2 8 57 18 1 4 100
9.
Y
X
18 26 34 42 50 58 N
x
12 3 7 2 12
20 2 8 6 16
28 3 50 4 5
36 2 6 8
44 2 1 1 4
52 2 1 3
n
y
3 12 62 18 3 2 100
10.
Y
X
16 22 28 34 40 n
x
14 3 3
20 7 2 3 12
26 2 8 50 60
32 6 4 2 12
38 6 3 9
44 4 4
n
y
12 16 57 8 7 100
11
Y
X
6 16 26 36 46
N
x
12 4 4
24 7 2 5 14
36 8 8 40 6 62
48 7 5 2 14
64

60 2 2 4
72 1 1 2
n
y
19 17 50 11 3 100
12.
Y
X
20 30 40 50 60 n
x
14 1 2 3
18 4 10 14
22 2 20 8 30
26 2 1 3
n
y
1 8 30 10 1 50
13.
Y
X
14 26 38 50 62 n
x
8 2 2 4
14 1 3 9 13
20 2 18 4 24
26 1 6 1 1 9
n
y
3 8 33 5 1 50
14.
Y
X
22 30 38 46 54 n
x
12 1 3 4
16 1 3 4
20 1 25 2 28
24 2 2 2 6
30 4 2 2 8
n
y
1 7 34 6 2 50
65
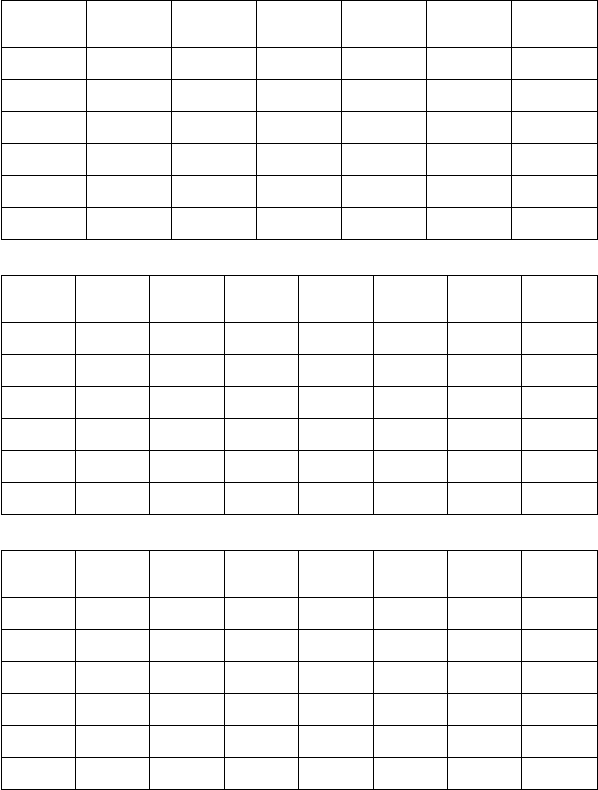
15.
Y
X
15 25 35 45 55 n
x
6 1 1 2
12 3 4 7
18 2 24 1 27
24 1 4 2 1 8
30 1 3 2 6
n
y
1 8 32 6 3 50
16.
Y
X
14 24 34 44 54 64 n
x
12 1 2 3
14 1 2 3 6
16 4 24 4 32
18 1 1 3 2 1 8
20 1 1
n
y
1 4 7 30 6 2 50
17.
Y
X
16 28 40 52 64 76 n
x
10 2 2
13 2 2 2 6
16 3 4 25 2 34
19 1 2 1 3 7
22 1 1
n
y
7 7 29 3 3 1 50
66
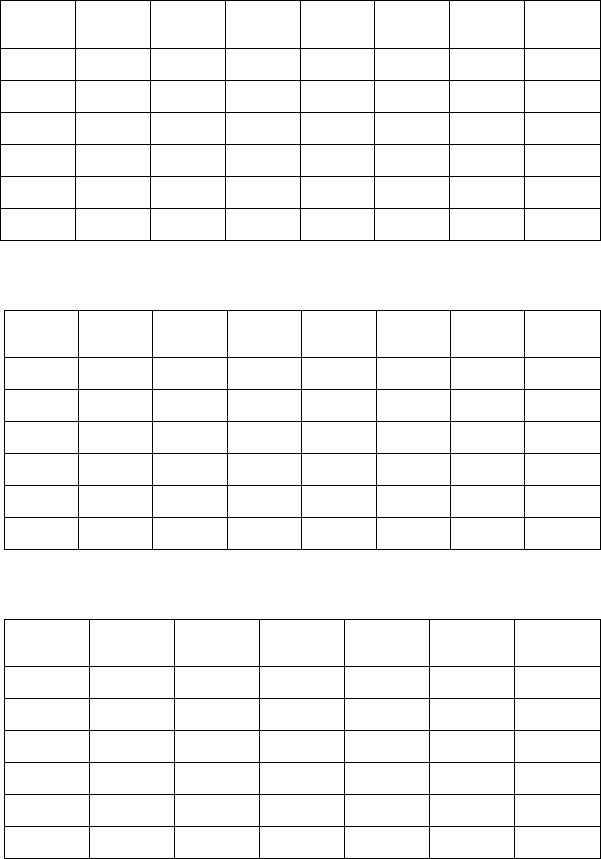
18.
Y
X
24 30 36 42 48 54 n
x
15 2 2 2 6
20 2 2 8 12
25 15 10 25
30 4 2 6
35 1 1
n
y
2 4 4 23 14 3 50
19.
Y
X
20 26 32 38 44 50 n
x
11 2 2 3 7
15 1 2 4 7
19 2 14 7 23
23 5 2 1 8
27 2 2 1 5
n
y
3 6 21 14 4 2 50
20.
Y
X
6 12 18 24 30 n
x
40 1 4 1 6
50 1 5 10 5 21
60 6 2 18 2 2 30
70 6 14 2 20
80 12 3 15
90 6 6
67
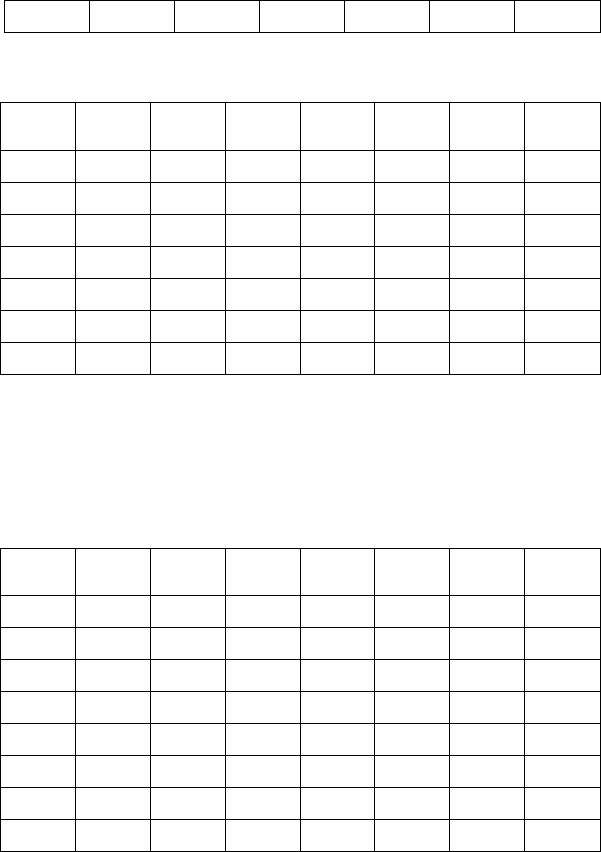
n
y
30 20 26 16 8 100
21.
Y
X
6 12 18 24 30 36 n
x
30 1 1 2 1 5
40 2 4 12 7 25
50 6 15 20 2 43
60 7 2 1 10
70 3 9 12
80 5 5
n
y
8 22 20 26 16 8 100
22.
Y
X
4 8 12 16 20 24 n
x
30 1 1
38 2 1 3
46 2 19 10 31
54 5 15 2 2 24
62 5 4 5 14
70 4 8 3 6 12
78 5 1 16
n
y
9 14 12 28 23 14 100
68

23.
Y
X
8 16 24 32 40 48 n
x
40 1 1 2
50 1 3 4
60 2 8 20 30
70 6 15 3 24
80 5 7 3 6 21
90 3 5 5 13
100 4 2 6
n
y
12 20 25 18 24 1 100
24.
Y
X
0 8 16 24 32 n
x
50 2 1 3
60 3 4 7
70 2 8 8 18
80 3 50 4 57
90 2 6 8
100 3 4 7
n
y
3 6 11 63 17 100
25.
Y
X
12 18 24 30 36 n
x
35 8 8
45 5 7 7 19
55 40 8 4 52
65 2 5 2 9
75 1 6 7
85 5 5
n
y
6 8 50 17 19 100
69

26.
Y
X
75 77 79 81 83 n
x
40 1 3 4
45 2 2 1 5
50 1 3 5 1 10
55 4 2 6
60 1 3 1 5
n
y
1 6 6 13 4 30
27.
Y
X
80 81 82 83 84 n
x
35 2 2 1 5
40 1 2 1 4
45 2 4 5 11
50 3 4 7
55 2 1 3
n
y
2 5 10 12 1 30
28.
Y
X
75 78 81 84 87 n
x
30 1 1 2
40 2 3 4 9
50 5 8 9 22
60 5 1 1 7
n
y
1 8 16 14 1 40
29.
70
