Хван М.П. Неистовая Вселенная: От Большого взрыва до ускоренного расширения, от кварков до суперструн
Подождите немного. Документ загружается.


Я н ко С л ава (Б и бл и отека Fort/Da) || http://yanko.lib.ru
Х ван М акси м П етро ви ч. Н еи стовая В сел ен н ая: О т Б о льш о го взры ва до ускор ен н ого
ра сш и рен и я , о т квар ков до суп ер стр ун . — М .: Л Е Н А Н Д , 2 0 0 6 . — 40 8 с.
171
171
кон ф ликт (антагони зм ) м еж ду общ ей теори ей отн осительн ости Э й н ш тейна и
квантовой м ехан и кой стал основн ы м проти воречи ем в соврем ен н ой ф и зике
элем ентарн ы х части ц , астроф и зи ке и косм ологии. П оэтом у дальнейш ее разви ти е
научного прогресса зави сит от того, как будет реш ен этот конф ли кт м еж ду общ ей
теори ей отн оси тельн ости и кван товой м ехани кой и в какой ф орм е будет п реодолен о
это основное противоречие в ф и зи ке части ц , астроф и зи ке и косм ологи и .
В оп рос о струн е как колеблю щ ей ся ф ундам ен тальн ой составляю щ ей
м и роздан и я является сам ы м главн ы м воп росом в теори и струн , поэтом у в
ф и лософ ском асп екте следует н а нем подробно и детально остан ови ться.
Д о создани я теори и струн госп одствую щ им ф и лософ ским м ировоззрен и ем бы ла
ф и лософ и я части ц : все состои т в кон ечн ом счете, так или иначе, из элем ентарн ы х
части ц . В качестве ф ундам ен тальн ы х части ц в ф изике элем ен тарны х частиц
рассм атри вали сь кварки и лептон ы : кварков ш есть — u-, d-, s-, с-, b- и t-кварк, а
леп тон ов такж е ш есть — е~, v
e
, μ , ν
μ
, τ-леп тон , ν
τ
. Т аким образом , в п рироде
сущ ествует си м м етри я м еж ду кваркам и и лептон ам и, т. е. полное соответствую щ ее
равенство м еж ду ф ун дам ен тальн ы м и частиц ам и.
К ром е эти х ф ун дам ен тальны х ф ерм ионов, участвую щ их в различн ы х
взаи м одействиях, сущ ествую т частиц ы -п ереносчи ки эти х взаим одей ствий:
части ц ам и п ерен осчи кам и являю тся ф отон ы как п ерен осчи ки электром агн и тны х
взаи м одействи й , глю он ы как п ереносчи ки сильны х ядерны х взаим одей ствий,
кали бровочны е бозоны W
±
и Ζ
0
как п ереносчи ки слабы х взаи м одей стви й и грави тон
как части ц а-переносчи к грави тационн ого взаим одействи я. Зн ачи т, частиц -
переносчи ков разли чны х взаи м одей стви й всего 12, вклю чая гравитон .
И так, 12 ф ундам ен тальн ы х ф ерм и он ов и 12 ф ундам ен тальн ы х бозон ов
составляю т 24 ф ундам ен тальн ы е части ц ы , п ри н и м аем ы е в рам ках ф и зи ки
элем ентарн ы х частиц .
В ы даю щ им ся достиж ени ем ф изики частиц является ф орм улирован и е
суп ерсим м етрии: всем эти м вы ш еперечи сленн ы м реально н аблю даем ы м (кром е
грави тон а) части ц ам соответствую т гип отетические суперпартнеры , которы е с
легкой руки Г елл-М ан н а получили н азвания — скварк, сэлектрон, сней три н о и т. д., а
такж е ф оти н о, глю ин о, вино и зино, а такж е грави тин о как суп ерп артн ер грави тон а.
В се эти части ц ы , осущ ествляю щ и е различн ы е взаи м одей стви я, и частицы -
переносчи ки этих взаим одействий — ф и зически различны е части ц ы , обладаю щ ие
различной м ассой и зарядом . Р азличны такж е констан ты и х взаи м одей ствий : сила
Э М В в 1 000 раз слабее С В , а сила С Л В п очти в 100 000 раз слабее С В , а сила Г В — в
10
-49
.
Т аковы м ногообразие и разнообрази е в м и ре ф и зи ки элем ентарны х части ц :
стандартн ая м одель н е дает и н е сп особн а дать единого теоретического объяснен и я,
исходя и н а основе единого ф ундам ен тальн ого п ри н ц и п а. О на н е способна давать
объясн ени е, п очем у сущ ествует различие м асс у частиц (и ли заряда); чем
определяется такая больш ая разн и ц а в кон стан тах взаим одействи й ; почем у м асса тау -
леп тон а в 4 000 раз больш е м ассы электрон а или м асса t-кварка п ревосходи т м ассу и -
или d-кварка в 40 200 раз. Н ам и звестн о только общ ее прави ло о том , что в сам ую
ран н ю ю эп оху п осле Б ольш ого взры ва образовались сверхтяж елы е, тяж елы е
части ц ы , которы е п о м ере похолодания В селенной расп адали сь п утем
последовательного распада и п ревращ али сь в обы чны е, н ам и наблю даем ы е легки е
части ц ы — кварки u и d или е
--
и ν
е
и т. д.

Я н ко С л ава (Б и бл и отека Fort/Da) || http://yanko.lib.ru
Х ван М акси м П етро ви ч. Н еи стовая В сел ен н ая: О т Б о льш о го взры ва до ускор ен н ого
ра сш и рен и я , о т квар ков до суп ер стр ун . — М .: Л Е Н А Н Д , 2 0 0 6 . — 40 8 с.
172
172
Н ам такж е н еи звестн о, почем у окруж аю щ ая н ас В селен н ая состои т только и з
первы х сем ей ств части ц — и - и d-кварка и е
-
и v
e
. Д ля чего сущ ествую т тяж елы е (и
сверхтяж елы е) частиц ы , с какой целью при рода и х породила? И т. д.
С тандартная м одель все эти м ногообразие и разнообрази е м ира частиц
рассм атри вает как эксп ери м ен тальн о наблю даем ы е входны е дан н ы е без еди н ого их
теорети ческого объясн ения. Н есм отря на зам ечательны е дости ж ен и я в рам ках
стандартн ой м одели , ей присущ и ф ундам ен тальн ы е н едостатки .
1. Т о, что он а оставляет, как м ы уж е п одчеркивали , в стороне гравитон как части ц у -
переносчи ка гравитационного взаи м одействия: квантово -п олевая теори я
грави таци и несостоятельн а из-за ее н есп особн ости сп равиться с возн и каю щ им и в
ходе столкновени й гравитон ов бескон ечн остям и.
2. Р азнообрази е и м н огообразие м ира ф и зики элем ен тарн ы х части ц не м огут бы ть в
рам ках стандартн ой м одели объяснен ы теоретически , и они остаю тся
ф еном ен ологическим и данн ы м и : они остаю тся ф еном енам и без п он и м ан и я и х
ноум ен ов как сущ ностей.
3. Т ретьи м недостатком стандартн ой м одели в ф и лософ ском ракурсе является то, что
сущ ествовани е элем ен тарны х части ц вы води тся в кон ечном счете из
сущ ествовани я сверхм ощ ны х тяж елы х частиц — хиггсов: частицы являю тся
продуктам и расп ада Х иггсовы х части ц , которы е ещ е экспери м ентальн о не
обнаруж ены и не откры ты . Э та конц епц и я порож ден и я части ц частиц ам и
представляет собой карти н у «зам кнутого проц есса», н аходящ егося в проти во речи и
с ф ун дам ен тальны м теорети чески м п олож ен и ем астроф и зи ки и косм ологии о том ,
что не всегда в сам ую ран н ю ю эп оху п осле Б ольш ого взры ва сущ ествовали
части ц ы , в том чи сле и ф ун дам ен тальн ы е — кварки и лептон ы (е
-
и v
e
): п осле
си н гулярного взры ва части ц ы возн и каю т и з сверхгорячей плазм ы в результате
«вы м ерзания». О дн и м словом , до появлени я части ц как результата «вы м ерзани я»
бы ло что-то «неопределен н ое», из которого возн и кает что -то определен н ое как
структурирован и е частиц. В аж но в ф илософ ском аспекте отм етить, что сначала
сам о сингулярн ое начало представляло собой н ечто абсолю тно неоп ределен н ое в
виде ап ей рон а А накси м андра, из которого (т. е. сверхгорячего и сверхп лотн ого) по
м ере расш ирен и я и похолодани я (т. е. п осле ин ф ляции) происходи т «вы м ерзани е»
ф ун дам ен тальн ы х части ц — кварков и электрон ов, которы е п ри н им аю т в рам ках
стандартн ой м одели как ф ундам ен тальн ы е. Н о они н е являю тся и не м огут бы ть
ф ун дам ен тальн ы м и , и бо теори я суп ерструн отказы вает частиц ам бы ть
ф ун дам ен тальн ы м и : ф ун дам ен тальны м и составляю щ им и н аш его м и роздан и я на
ультрам икроскопическом уровн е, разм ер которого сравни м с план ковской дли н ой
10
-33
см , являю тся н е части ц ы , а колеблю щ иеся одн ом ерны е струны , резон ансны е
колебани я которы х порож даю т все элем ен тарны е части ц ы и их ф ун дам ен тальны е
свой ства — м ассу и заряд, в том числе и цветовой: каж дая элем ен тарная частица
содерж ит вн утри себя колеблю щ ую ся струну и поэтом у во всех без исклю чени я
части ц ах находятся и м м ан ентны е колеблю щ иеся струны , вибраци и , дрож ани е
которы х определяю т и порож даю т все ф ундам ентальн ы е свойства частиц — м ассу
и заряд. Р езон ансны е колебани я струн ы такж е определяю т кон станты
взаи м одействий , си ла которы х зави сит от ин тенсивн ости резонан сн ы х колебаний
струн .

Я н ко С л ава (Б и бл и отека Fort/Da) || http://yanko.lib.ru
Х ван М акси м П етро ви ч. Н еи стовая В сел ен н ая: О т Б о льш о го взры ва до ускор ен н ого
ра сш и рен и я , о т квар ков до суп ер стр ун . — М .: Л Е Н А Н Д , 2 0 0 6 . — 40 8 с.
173
173
Е щ е раз м ы хоти м подчеркн уть ф и лософ ский аспект н ам и рассм атриваем ы х
проблем . Ч асти ц ы как таковы е сущ ествую т п остольку, п оскольку во всех н и х
присутствую т струны , которы е оп ределяю т их бы ти й н ы й ф и зи чески й статус:
независим о от того, являю тся ли части ц ы ф ерм ионам и (т. е. кваркам и и ли лептон ам и
— электронам и или электронны м и н ейтрино) и ли бозон ам и (частиц ам и -
переносчи кам и разн ы х взаим одействи й — ф отон ам и, глю он ам и , кали бровочны м и
бозон ам и и грави тон ам и), их ф и зи ческое бы ти е оп ределяет и орган и зует их в их
структурны х целостн остях не п росто струны , а струн ы колеблю щ и еся: резон ансны е
колебани я струн ы создаю т все элем ен тарны е частицы и их ф ун дам ен тальн ы е
свой ства — м ассу и заряд, в том чи сле кварковы й цветовой заряд. П оэтом у эти
резонан сны е колебани я струн и оп ределяю т кон станты разны х взаим одействи й —
С В , С Л В , Э М В и Г В . Ч асти ц ы разли чн ы , а струн ы как таковы е все иден ти чны ,
одинаковы е, тож дественн ы е: тож дество создает и твори т разли чи е — м ногообразие и
разн ообразие в м ире элем ентарны х части ц .
Н о как и каким образом тож дество творит реальное ф изическое различие?
П отом у что это тож дество — реальн ое тож дество, а не ф орм альное: струн ы
тож дественн ы и вм есте с тем он и разли чаю тся п о характеру колебан и й . В се зави сит
от характера интен сивности колебани й струны , т. е. от м оды колебан и я струн ы : м ода
колебани я струн ы — сп особ и характер колеб ани я струн ы . К олебан и е — это не
бы тие струн ы , а ее сущ ность: сущ ностью струн ы является колебани е (ви браци я,
дрож ан и е, осци лляци я). В н е колебани й , вне ви браци й н ет струн . И м ен н о ви брац и и ,
колебани я струн ы все определяю т и все создаю т и творят: колебани е есть суть
струн ы .
В от как оп и сы вает зам ен у точечн ы х частиц струн ам и в качестве
ф ун дам ен тальн ы х ком пон ентов м ироздан и я автор зам ечательной книги «Э леган тная
В селенная» Б райан Г рин , которы й отм ечает, что эта зам ен а ведет к далеко и дущ и м
последстви ям . «П ервое и сам ое главн ое состоит в том , что теори я струн , по -
види м ом у, разреш ает п роти воречи е м еж ду общ ей теорией отн осительн ости и
квантовой м ехани кой. К ак м ы уви ди м н и ж е, пространствен н ая п ротяж ен н ость струн
является н овы м клю чевы м звеном , позволяю щ им создать един у ю гарм оничную
си стем у, объедин яю щ ую обе теори и . В о -вторы х, теори я струн действи тельно
представляет объединяю щ ую теори ю , п оскольку в н ей все вещ ество и все
взаи м одействия обязаны свои м п рои схож дени ем одн ой ф ундам ентальн ой вели чиной
— колеблю щ ей ся струн ой. Н акон ец , — продолж ает Б райан Г рин , — как будет
показан о более п одробн о в последую щ их главах, пом им о эти х блестящ их
дости ж ен и й , теори я струн ещ е раз ради кальн о и зм ен яет н аш и п редставлени я о
простран стве-врем ен и » (Г рин Б . Э легантн ая В селен н ая. М .: У Р С С , 2004. С . 96).
И з этих вы сказы ван и й автора вели колепной кни ги п о глубин е рассм атриваем ы х
им слож ней ш их п роблем и доступн ости (без детальн ы х м атем атических вы кладок и
техн и чески х п одробностей ) излож ени я и х, Б рай ана Г ри н а, м ы отм етим только три
м ом ента:
1. Т еория суперструн Б . Г ри н ом рассм атри вается как окон чательн ая теори я, закон ы
которой н е требую т объяснен и я други м и, более глубоким и законам и при роды : она
является последн ей окончательн ой теори ей, объясняю щ ей все виды м атерии и все
си лы взаим одействий в п рироде.
2. О днако позиц и я Б рай ан а Г ри н а отличается в этом вопросе от позиции
Н обелевского лауреата С тивена В ай н берга, которую он отстаи вает в своей кни ге
«М ечты об окон чательной теори и »: п озиция Б рай ана Г рина не так категоричн а и
однозначн а, как п ози ц и я С ти вена В айнберга. С . В айн берг, как убеж ден н ы й
редукц и он и ст, счи тает, что сущ ествует окончательная теори я, закон ы которой не
требую т

Я н ко С л ава (Б и бл и отека Fort/Da) || http://yanko.lib.ru
Х ван М акси м П етро ви ч. Н еи стовая В сел ен н ая: О т Б о льш о го взры ва до ускор ен н ого
ра сш и рен и я , о т квар ков до суп ер стр ун . — М .: Л Е Н А Н Д , 2 0 0 6 . — 40 8 с.
174
174
объясн ени я другим и , более глубоким и закон ам и при роды : еди н ствен н ы м
претенден том на роль этой окон чательной теори и является теори я суп ерструн . П ри
этом С . В айн берг добавляет, что проблески окончательн ой теори и в виде
разрабаты ваем ой н ы н е теори и суп ерструн ви дны : законы теории суп ерструн
представляю т собой последние, окончательны е законы природы , н е требую щ ие их
объясн ени я более глубоки м и законам и.
Ч то касается Б рай ана Г рин а, то его позиц и я н е так категоричн а и н епри м ирим а,
как позиц и я С тивена В ай н берга. Б райан Г рин п одходит к воп росу об окончательной
теори и о законах природы более м ягко и терпи м о, т. е. его пози ц и я более толерантн а:
теори я суперструн ещ е не м ож ет п ретендовать на роль «теори и всего сущ его»
(«В С »). О н а м ож ет стать со врем ен ем такой «теорией всего сущ его», н о м ож ет
случиться так, что н а см ену теории суп ерструн при дет другая, более глубокая,
всеохваты ваю щ ая теория. Н ам , безусло вн о, в ф и лософ ском ракурсе более
им п он и рует толеран тная п ози ц и я автора п ревосходн ой во всех отнош ени ях,
особен н о в ф илософ ском , книги «Э леган тная В селенн ая».
3. В опрос окончательн ой теори и п о сущ еству есть вопрос ф илософ ский в двух
отн ош ени ях: н аш е знани е о В селенн ой в ее м акро- и м и кром ирах является ли
полн оц енн ы м и абсолю тн ы м и ли неп олны м и неокон чательн ы м ? П уть прогресса
науки терни ст: н и кто н а этот ф и лософ ский вопрос не м ож ет ответить однозн ачн о
и категори чески . (К то м ог подум ать 50-60 лет том у назад о К Х Д , электрослабой
теори и , стандартной м одели ф изики элем ентарны х части ц и ли о черн ы х ды рах
(звездн ы х и сверхм асси вн ы х в ядрах акти вн ы х галакти к) и т. д. 10 лет том у н азад
никто не знал о сущ ествован и и косм ического вакуум а как си лы ан тигравитации,
ан ти тяготени я, тем ны м п ятн ом для нас все ещ е остается «тем н ое вещ ество»,
природа которой остается неразгадан н ой тайн ой , и т. д. и т. п.)
П оэтом у утверж ден и е о том , что теори я суп ерструн охваты вает все ви ды
м атерии и силы взаи м одей ствий в п ри роде и их объясн яет, не совсем корректн о: она
охваты вает и объясн яет все нам и звестн ы е и наблю даем ы е ви ды м атерии и си лы
взаи м одействий . Н е означает ли это, что в п ри роде больш е н ет никаких других ви дов
м атерии и си л взаи м одействий, которы е м огут бы ть человечеством п ознаны через 50-
100-1000 лет?! И ны м и словам и, огран и чи вается вся н аш а В селен н ая только н ам в
дан н ы й м ом ен т врем ени и звестн ы м и и п озн анн ы м и ви дам и м атери и и си л
взаи м одействий : в н астоящ и й м ом ен т врем ен и блестящ и е и ф ундам ен тальн ы е
научны е достиж ен и я и откры ти я ф и зи ки части ц , астроф изики и косм ологи и —
только часть, ф рагм ен т, «кусочек» больш ой В селен н ой .
Н ам п редставляется и н тересн ы м и ф илософ ски плодотворн ы м утверж ден и е
автора «Э легантной В селен н ой » Б . Г ри н а, ан али зи рую щ его хаоти ческую
косм ологи ю А н дрея Л и н де, которы й работает в настоящ ее врем я в С тэн ф ордском
уни верси тете С Ш А . С огласно хаотической косм ологии Л и н де, сущ ествует н е одна
наш а В селенная, а бесконечн ое м нож ество м ульти -вселенн ы х, объеди н енн ы х в М ега-
В селенную . В каж дой м ульти -вселенн ой свои закон ы природы , отличны е от законов
в други х м ульти-вселенны х, и, следовательн о, своя м атери я, свои п ространство -
врем я и свои особы е взаим одействи я: если ж е станет возм ож н ы м контакт с этим и
м ульти-вселен н ы м и , то н аш е п озн ан и е закон ов п ри роды н е м ож ет бы ть
окон чательны м и поэтом у достиж ен и е окон чательн ой теори и н еосущ естви м о. В
прогрессе н ауки н евозм ож на последняя станц и я остан овки: лю бая станц и я —
пром еж уточн ы й пункт остановки.

Я н ко С л ава (Б и бл и отека Fort/Da) || http://yanko.lib.ru
Х ван М акси м П етро ви ч. Н еи стовая В сел ен н ая: О т Б о льш о го взры ва до ускор ен н ого
ра сш и рен и я , о т квар ков до суп ер стр ун . — М .: Л Е Н А Н Д , 2 0 0 6 . — 40 8 с.
175
175
§ 3. А м би ц и озн ость суп ер стр ун н ы х теор и й
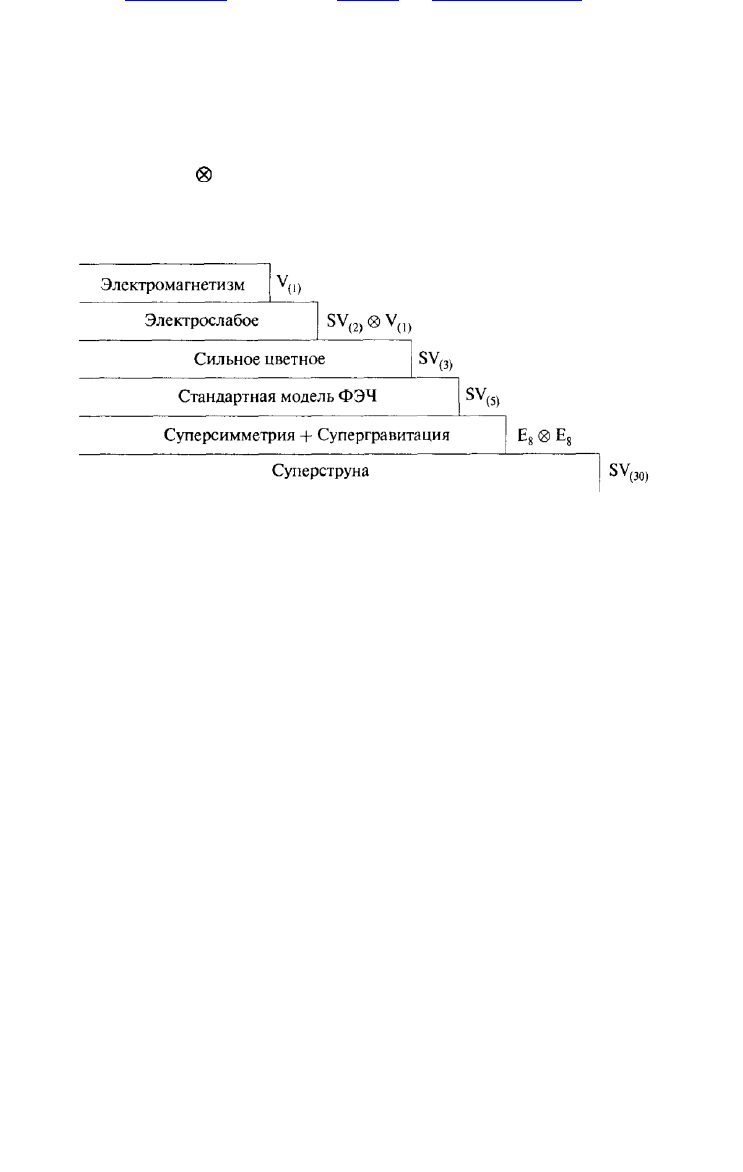
С уперструн н ая групп а SO(32) и E
8
E
8
— сим м етрия кали бровочны х
преобразован и й как м акси м ально -расш и ренн ая груп п а сим м етри и кали бровочн ы х
преобразован и й , п одгруп п ой которой являю тся н е только стандартн ая м одель ф и зики
элем ентарн ы х части ц — SU
(5)
и супертеори я Я нга— М иллса, н о и суп ерсим м етри я и
суп ергравитац и я. П оэтом у групп а Г рина— Ш варц а SO(36) или Eg E
8
как групп а
си м м етри и кали бровочн ы х преобразован и й — м акси м альн о-расш и ренн ая груп п а
си м м етри и . О на и склю чительн о обш ирн ая груп п а кали бровочн ы х п реобразован и й ,
когда-либо знаком ая нам .
С уперструн н ая теори я требу ет отказа от идеализированн ы х точечны х части ц ,
вы работанны х ещ е древн и м и грекам и (Д ем окри том — Л евкиппом ) более 2500 лет
том у н азад. Г рави таци я долж н а бы ть связана со всем и другим и ти п ам и
взаи м одействий н а п лан ковском м асш табе т
рl
= 10
19
Г эВ , что соответствует длин е l
pl
= 10
-33
см и врем ени t
pl
= 10
-44
с. П оэтом у возн и кает н еобходи м ость создан и я
квантовой теори и грави таци и . Ч етвертое состоит в том , что суп ерструн н ы е теори и
перепры ги ваю т «пусты н ю », где п олны м -полно долж ны киш м я ки ш еть разли чн ы е
экзоти чески е части ц ы и сверхси лы и х сверхвзаим одей ствий: для исследования
«пусты н и » необходим десертрон ради усом н аш ей галакти ки .
А м бициозность суп ерструн н ы х теори й заклю чается ещ е и в том , что ставится
вопрос о сам ом бы ти й н ом статусе элем ентарн ы х частиц .
М ы уж е отм ети ли , что струнная м одель разрабаты валась в связи с адронн ой
ф и зи кой ещ е в 60-е гг. п рош лого столети я.
С уперструн ы строятся в двух различаю щ ихся топологиях: одни струн ы —
откры ты е со свободны м и концам и , а другие — зам кнуты е. С труны обладаю т ещ е
внутрен н и м и степен ям и свободы . В откры ты х струнах со свободн ы м и конц ам и
квантовы е чи сла расп олагаю тся на этих свободн ы х кон ц ах, а в зам кнуты х струн ах
квантовы е чи сла разм азаны п о всей струн е.
С трун ы такж е обладаю т внутренн ей ори ентаци ей: он и бы ваю т ориентирован н ы е
и н еори ентированн ы е. А взаи м одей стви е м еж ду суп ерструнам и осущ ествляется
путем разры ва струны и соединен и я двух струн. Э лем ен тарн ы е части ц ы в
суп ерструнн ы х м оделях рассм атри ваю тся как квантово -п олевы е возбуж дени я струн,
которы е обладаю т вращ ени ем и вибраци ей.
К вантово-п олевы е возбуж дени я (вращ ен и е и ви брация) рассм атри ваю тся как
наблю даем ы е эксп ери м ен тально элем ентарн ы е частиц ы . В ся «н и зкоэнергетическая
ф и зи ка» вклю чается в состав суперструнн ой теори и .
С уперструн н ая теори я долж н а бы ть си м м етри чн ой : он а си м м етри чн а н е в
обы чн ы х п ространствах, а в п ространствах вы сш и х разм ерн остей , которы е
разрабаты вали сь К алуц ей — К лейн ом для осущ ествлени я м ечты А . Э йнш тей н а об
объеди н ени и гравитации и электром агнети зм а в 20 -е гг. прош лого века: в ней си лы
истолковы вали сь как п ространства вы сш их разм ерностей для объедин ени я
электром агн ети зм а и гравитаци и н а чи сто геом етри ческой основе.
В своей теории Г ри н и Ш варц рассм атри ваю т п ространство 10 изм ерений: 4 —
наш четы рехм ерны й реальны й м и р — и 6 ком п акти ф и ц и рован н ы х разм ерн остей, т. е.
неви ди м ы х и нен аблю даем ы х.
П рирода суп ерструн п роявляется н а эн ергиях вы ш е м асш таба П ланка: m
pl
=
10
19
Г эВ , l
рl
= 10
-33
см , t
рl
= 10
-44
с.
Я н ко С л ава (Б и бл и отека Fort/Da) || http://yanko.lib.ru
Х ван М акси м П етро ви ч. Н еи стовая В сел ен н ая: О т Б о льш о го взры ва до ускор ен н ого
ра сш и рен и я , о т квар ков до суп ер стр ун . — М .: Л Е Н А Н Д , 2 0 0 6 . — 40 8 с.
176
176
К вантовая теори я и О Т О воплощ аю т всю сум м у человеческих знани й о п рироде
В селенной: ош елом ляю щ ий ди ап азон п ознан и я нам и м и ра в 45 п орядках. В
м и кром и ре ди апазон п ознан и я дости гает 10
-17
см , а в К осм осе — 10 см .
К али бровочная группа сим м етри и калибровочн ы х п реобразовани й Г рина—
Ш варца вклю чает E
8
E
8
, суп ертеорию Я нга— М иллса, О Т О , суперграви тацию и
стандартн ую м одель ф и зи ки элем ентарны х частиц .
Р и с. 1.29
К али бровочная теория как еди н ое и свободн ое от ан ом али й и расходи м остей —
опи сани е кван товой гравитаци и .
Э то револю ци он н ы й п роры в в разви ти и соврем ен н ой ф и зи ки точечны х части ц .
С м ена точечн ой ф и зики суп ерструнн ой ф и зи кой — револю ци я п ерехода от
ф и лософ и и точечн ой к суп ерструн н ой ф илософ ии: есть окон чани е эры точечной
ф и лософ и и в ф и зи ке и н ачало н овой эры суперструн н ой ф и лософ и и в ф и зи ке части ц .
К варки и и х суп ерп артнеры в суп ерсим м етри и рассм атриваю тся как точечн ы е
части цы . С уп ерсим м етри я есть теори я, позволяю щ ая объясн и ть и пон ять точечн ы е
части ц ы с п ом ощ ью точечн ы х суп ерчасти ц : точечн ы е части ц ы объясн яю тся с
пом ощ ью суперсим м етри чн ы х суперп артнеров. В квантовой грави таци и такж е
грави тация и столковы вается и рассм атри вается как взаи м одей ствие м еж ду
грави тон ам и как точечны м и части ц ам и.
С уперсим м етри я вклю чает в себя суп ерграви таци ю как подм нож ество: в
суп ерсим м етрии грави тон им еет суп ерп артн ера — грави тин о. Г равитин о как
суп ерп артн ер грави тон а есть точечн ая части ц а. П оэтом у происходи т то ж е сам ое — с
пом ощ ью точечн ы х части ц объясн и ть и п онять те ж е точечн ы е части ц ы : в этом суть
суп ерсим м етрии и супергравитации.
К вантовая теори я поля как теория Я н га— М иллса локальн ой сим м етри и
связы вает точечн ы е части ц ы с п ространством -врем ен ем п арам етрам и ж естко.
В н утрен н и е степ ени свободы части ц ы связаны с внеш н и м и п ространственн о -
врем енн ы м и степеням и свободы .
Т очечн ы е частицы связаны ж естко с п ри н ц и п ом при чи н н ости , локальности ,
неп реры вн ости , ун и тарн ости . С ледовательно, необходи м отказ от всех п очи таем ы х
постулатов при роды . П оэтом у суп ерструнн ая теори я долж н а вклю чать в себя всю
«ни зкоэн ергети ческую ф и зи ку»: эн ергии ниж е 10
15
Г эВ .
Л окальная квантовая теория, оп ери рую щ ая точечн ы м и частицам и , содерж ит
расходи м ости на эн ерги ях вы ш е т
рl
= 10
19
Г эВ . В ообщ е следует отм етить (это важ но
для

Я н ко С л ава (Б и бл и отека Fort/Da) || http://yanko.lib.ru
Х ван М акси м П етро ви ч. Н еи стовая В сел ен н ая: О т Б о льш о го взры ва до ускор ен н ого
ра сш и рен и я , о т квар ков до суп ер стр ун . — М .: Л Е Н А Н Д , 2 0 0 6 . — 40 8 с.
177
177
ф и лософ и и ), что отказ от и деализи рован н ы х точечн ы х частиц необходи м о правильно
ф и лософ ски истолковать:
1) отказ означает отказ от точечн ы х части ц как элем ен тарн ы х объектов;
2) отказ означает отказ от рассм отренн ы х то чечн ы х частиц н а основе локальн ой
кали бровочной сим м етри и (т. е. от простран ственно -врем ен н ой точки к точке);
3) ф и зическую реальн ость н е обязательн о рассм атри вать в виде точечн ы х частиц ,
взаи м одействую щ их локально от одн ой пространствен н о -врем енн ой точки к
другой точке: это означает, что в суп ерструнн ой теории ф изическая реальн ость н е
подчиняется теори и Я н га— М и ллса, благодаря которой точечн ая ф и зика, т. е.
квантовая локальная теория, доби лась несом н енн ы х и блестящ их успехов; речь
идет об отказе от одного и з ф ундам ентальны х п ри н ц и п ов м иропон и м ани я, т. е. от
точечн ого м иропон и м ан и я (от точечн ой ф и лософ и и ).
В озрож ден и е исследовательского и н тереса к струнам началось в 1984 г., когда
Г ри н и Ш варц сф орм улировали суперструн н ую теори ю в 10 и зм ерени ях — с
пом ощ ью груп п вн утрен н ей сим м етри и SO(32) и E
8
E
8
:
1. Г руп п а вн утрен н ей сим м етри и Е
8
вклю чает в себя всю «низкоэнергетическую
ф и зи ку», т. е. всю ф изику н и ж е эн ергий 10
15
Г эВ . С ледовательн о, Eg вклю чает всю
стандартн ую м одель ф и зики элем ен тарн ы х частиц SU
(5)
в качестве п одгруппы .
2. Д ругая группа Е
8
п редставляет собой гравитационны е взаим одей ствия в наш ей
В селенной.
К вантовая теори я гравитации — точечн ая, локальная теори я взаим одействия
м еж ду грави таци он н ы м и точечн ы м и части ц ам и. В суп ерструнн ой теории грави таци я
рассм атри вается как обм ен м еж ду зам кн уты м и струнам и . П оэтом у если у грави тон а
обнаруж и тся, действительн о, суперп артн ер — грави тин о, то эта суп ерсим м етри чн ая
части ц а м ож ет п ретендовать на роль «тем ной м атери и »: и грави тон , и гравитин о как
суп ерп артн еры есть части ц ы точ ечны е, которы е долж н ы п одчи н яться всем
квантовы м калибровочны м и локальны м закон ам теори и Я н га— М иллса; в
суп ерструнн ой теории точечн ы е части ц ы суть возбуж дени я струн : он и образую тся и
взаи м одействую т путем разры ва струн и объеди н ени я двух струн.
О дн и м словом , как все известн ы е элем ен тарны е части ц ы (кварки, леп тон ы и
другие), так и грави тон ы и их суперсим м етричны е суп ерпартнеры гравитин о суть
возбуж ден и я струн : возбуж дени я — кван тово-м ехан и ческие вращ ени я, вибрац и и ,
резонан сы .
Т очечн ы е части ц ы суть возбуж ден ия струн . В этом состои т ф илософ ия
суп ерструнн ой ф и зи ки.
С трун а ф ундам ентальн а: один объект генери рует м н ож ество элем ен тарн ы х
части ц .
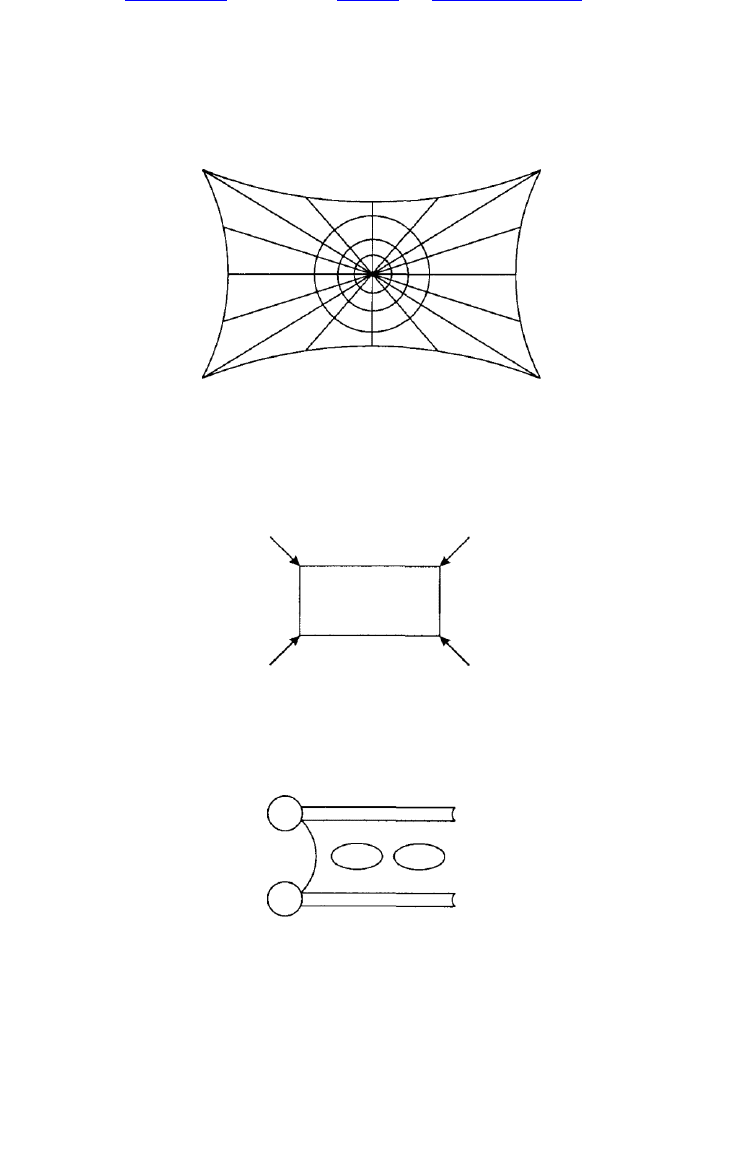
Р и с. 1.30
1. Г равитаци я у Н ью тона рассм атри вается как си ла, п ередаю щ аяся м гн овенн о на
расстояни и :
Я н ко С л ава (Б и бл и отека Fort/Da) || http://yanko.lib.ru
Х ван М акси м П етро ви ч. Н еи стовая В сел ен н ая: О т Б о льш о го взры ва до ускор ен н ого
ра сш и рен и я , о т квар ков до суп ер стр ун . — М .: Л Е Н А Н Д , 2 0 0 6 . — 40 8 с.
178
178
2. А у Э й н ш тейн а грави тация рассм атри вается как кри ви зна п ространственно -
врем енн ого м н огообрази я:
Р и с. 1.31
3. В теори и квантовой гравитаци и рассм атри вается грави таци я как взаи м одействие
м еж ду грави тон ам и как точечн ы м и части ц ам и. П ри бавляется теперь к
эйнш тей н овском у поним ани ю гравитации:
Р и с. 1.32
4. В суп ерструн н ой теори и грави тация рассм атри вается как обм ен м еж ду
зам кнуты м и струнам и :
Р и с. 1.33
М ы рассм отрели теори и В ели кого объедин ени я — м и н и м альная м одель —
(SU
(5)
) и суперсим м етри я: эти теорети чески е м одели им ею т свои преим ущ ества и
недостатки . М ы не будем их перечи слять: сам ы м больш им недостатком К Х Д
является конф ай н м ен т (кварков ни кто не видел), а для суп ерсим м етри и главны м
недостатком является отсутствие эксперим ен тальн ы х ф актов, подтверж даю щ их
суп ерсим м етричны е м одели.
О дн ако не эти собы тия вы звали к возвращ ен и ю суп ерструн н ы е м одели , которы е
активн о и интен сивно разрабаты вались ф и зи кам и в связи с адрон н ой ф и зикой в 60 гг.
прош лого века, — т. е. с проблем ой кон ф айн м ента.

Я н ко С л ава (Б и бл и отека Fort/Da) || http://yanko.lib.ru
Х ван М акси м П етро ви ч. Н еи стовая В сел ен н ая: О т Б о льш о го взры ва до ускор ен н ого
ра сш и рен и я , о т квар ков до суп ер стр ун . — М .: Л Е Н А Н Д , 2 0 0 6 . — 40 8 с.
179
179
С ущ ествует главная ф ундам ен тальн ая п роблем а ф и лософ и и единого описани я
всего. Э та ф илософ ская п роблем а кон кретизируется в н еобходи м ости объедин ени я
двух вели ких ф и зи чески х теорий Х Х в. — кван товой м ехани ки и О Т О Э й н ш тейна —
на единой теоретической осн ове.
П арадоксально, но ф акт остается ф ак том : квантовая теори я и теори я
отн оси тельн ости (О Т О ) вм есте даю т нам всю сум м у человечески х знани й о м ире
м и крочасти ц и В селен н ой , т. е. о п ри роде, одн ако он и разви вались изоли рован н о,
никогда и нигде не п ересекаясь друг с другом . К ак будто в п ри роде, отм ечает М .
К аку в своей кни ге «В ведени е в теори ю струн », сущ ествую т два ум а: оди н познает
м и кром и р, а другой — В селенн ую в целом .
К вантовая теори я добилась блистательны х усп ехов в п ознан и и м алого во
В селенной, а О Т О — больш ого в ней . О бщ ая теория отн осительн о сти , сотворен н ая
ген и ем одного человека, — еди н ственн ая теори я о В селенн ой в ц елом : она оп и сы вает
красоту м ира и соверш енство его строен и я и структурн ой орган и зац и и . П ока нет
ф и зи ческой теори и , способн ой конкури ровать в познани и сам оорган и заци и
В селенной в ее крупн озерн и сты х и круп н ом асш табны х образован и ях (звезды ,
галакти ки , скоплен и я, сверхскоп ления): он а дает н ам ц елостн ое зн ан и е об эволю ции
В селенной, ф акти чески ц елостное ф и лософ ское м и ропоним ани е о В селен н ой , ее
рож ден и и , эволю ц и и и дальнейш ей судьбе: О Т О , как отм ечаю т специ али сты , —
сам ая изящ ная и сам ая строгая м атем ати чески -ф изи ческая теори я, когда-либо
сотворен н ая человеческим гени ем .
Н е м енее красивая и и зящ н ая ф и зико -м атем атическая теори я — кван товая
м ехани ка (кван товая теория поля): она дает н ам возм ож ность п роникн уть в сам ы е
ф ун дам ен тальн ы е и глубокие слои строен и я и структуры м атерии . К ван товая теори я
поля дает нам возм ож ность п озн ать и исследовать сам ы е глубин н ы е основани я
наш его м ироздани я: в косм осе м ы прони кли до 10
28
см , а в м и кром ире — до 10
-17
см .
Т аки м образом , две великие теори и Х Х в. — кван товая теория п оля и О Т О — даю т
вм есте сум м у н аш его знан и я о м и ре в 45 п орядках: это вели кое дости ж ен и е
человеческой м ы сли .
О дн ако это знан и е о м и ре не есть еди н ое зн ани е о нем : ф и лософ ское знан и е о
м и ре н е м ож ет бы ть сум м ой о м ире, а ц елостн ое еди н ое знан и е. О дн о во всем и все в
одном .
Н ельзя сказать, что не бы ло поп ы ток объедин ени я кван товой теори и поля и
О Т О : их бы ло м н ож ество, но все эти п опы тки вдребезги разби вали сь об, казалось,
неп реодолим ы е трудности построения одн ой теори и всего сущ его.
О сновн ы м и трудностям и О Т О Э й н ш тейна бы ли:
1. В се реш ени я общ и х уравнени й О Т О Э й н ш тейн а н еизбеж но при водят к
си н гулярной точке, где закон ы О Т О становятся н епри м еняем ы м и (м ы об этом
узнаем , когда будем рассм атри вать про блем у черны х ды р).
2. Б ез кван товой грави тации (т. е. О Т О ) соверш енно бессм ы сленн о ставить воп рос об
объеди н ени и кван товой теории и О Т О . О днако, как отм ечает М . К аку, н аивн ая
вера в возм ож н ости кван тован и я О Т О всегда кон чалась п ровалом .
3. В се квантовы е теории об элем ен тарн ы х частицах, как м ы показали вы ш е,
осн ован ы на кали бровочной теории , ф ун дам ен тальн ы м достиж ением которой
является п еренорм и ровка, т. е. возм ож ность устрани ть бескон ечн ы е расходим ости :
неп еренорм и руем ая теори я в принципе не п роверяем а, а О Т О — теори я
неп еренорм и руем ая.

Я н ко С л ава (Б и бл и отека Fort/Da) || http://yanko.lib.ru
Х ван М акси м П етро ви ч. Н еи стовая В сел ен н ая: О т Б о льш о го взры ва до ускор ен н ого
ра сш и рен и я , о т квар ков до суп ер стр ун . — М .: Л Е Н А Н Д , 2 0 0 6 . — 40 8 с.
180
180
К вантовая теория п оля дости гла блестящ их и внуш ительны х успехов н а п ути
построен и я калибровочн ы х квантовы х теори й частиц и си л их взаи м одействи й :
построен ы калибровочны е теории электрослабы х взаи м одей ствий , К Х Д и
стандартн ая м одель ф и зики элем ентарн ы х части ц —
Н есм отря н а огром ны е усп ехи в п остроен и и кали бровочны х кван товы х теори й
части ц и сил их взаи м одействий , в сторон е остали сь осн овн ы е трудн ости теории
В ели кого объеди н ени я.
Н а пути объединен и я теори й всего сущ его им ею тся, как отм ечает М . К аку,
почитаем ы е п редставлени я о п ри роде, вы работанны е н а протяж ен и и всей истори и
ф и лософ и и и науки. О ни следую щ ие:
1) неп реры вн ость;
2) причи н н ость;
3) ун и тарность;
4) локальность;
5) точечн ы е части ц ы .
М . К аку считает, что необходи м о отказаться от одно го и ли н ескольки х
почитаем ы х представлений о при роде, сф орм ули рованн ы х на уровне здравого
см ы сла.
С ам ы м безболезн енн ы м счи тает М . К аку отказ от идеологи и и деали зи рованн ы х
точечн ы х частиц : отказ от и деализи рован н ы х точечн ы х части ц для построен и я
суп ерструнн ы х м оделей не н аносит н и какого вреда н и кван товой теории поля, ни
О Т О .
К лю чом к объединен и ю кван товой теории поля и О Т О является калибровочн ая
си м м етри я, т. е. груп п а кали бровочны х преобразован и й .
К ак м ы показали , все кван товы е теори и ф и зики элем ен тарны х части ц являю тся
кали бровочны м и теори ям и, ф ун дам ен тальны м и дости ж ен и ям и которы х являю тся
перенорм ировка, отсутстви е аном али й и расходим остей, груп п а си м м етри и ,
безм ассовы е калибровочны е бозоны и другие требования.
В се п оп ы тки связать грави тацию с ф и зикой элем ентарн ы х части ц
обескураж и ваю щ е разбивали сь вдребезги из-за невозм ож н ости устрани ть
бесконечн ости (расходи м ости). И м ен н о поэтом у все поп ы тки п остроен и я квантовой
теори и грави таци и неи зм енн о оказы вали сь безуспеш ны м и : без объедин ени я
грави тации со всем и другим и силам и взаи м одействий — С Л В , Э М В и С Ц В —
абсолю тн о и склю чено создани е единой теори и всего сущ его.
Н астоятельная необходим ость создани я кван товой теории грави тации
вы зы вается в суперструн н ы х м оделях тем , что в суп ерструн н ы х м оделях и сследуется
ф и зи ческая реальн ость в п лан овски х м асш табах м ассы , длины и врем ени :
когда обязательны м требован и ем является учет гравитац и он н ы х эф ф ектов. П оэтом у
ф и зи ки и косм ологи возлагаю т больш и е н адеж ды н а теори ю суп ерструн , где возм ож -
