Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.


47. 1, i, i
49. (1 3
i)/2, (1 3
i)/2, and 1
51. 12 trips around the circle
53. Since the u
i
are distinct, clearly, the vu
i
are distinct. Since v
is a solution of z
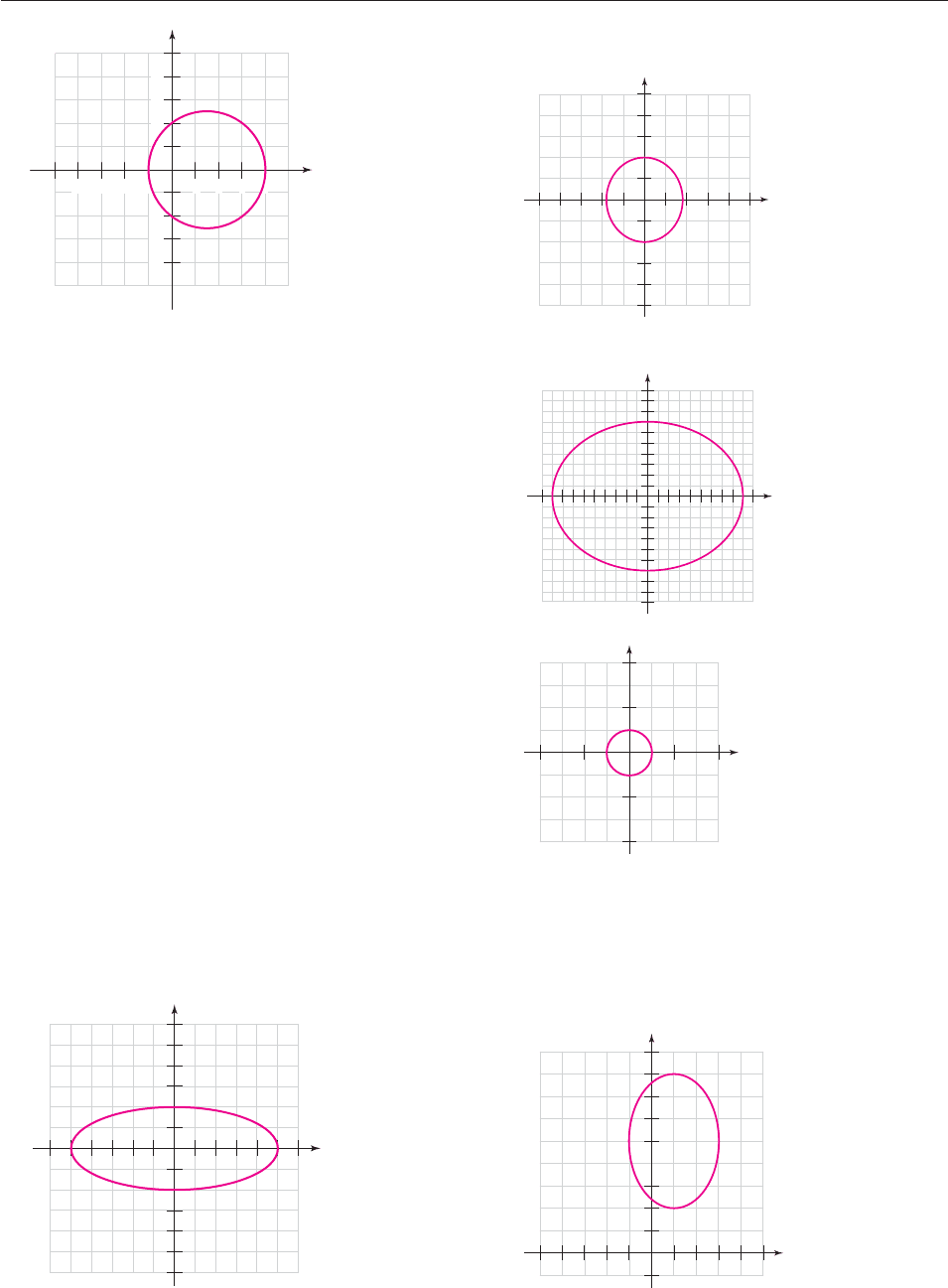
n
r(cos u i sin u), we can write
v
n
r (cos u i sin u), and similarly u
i
n
1. Then
(vu
i
)
n
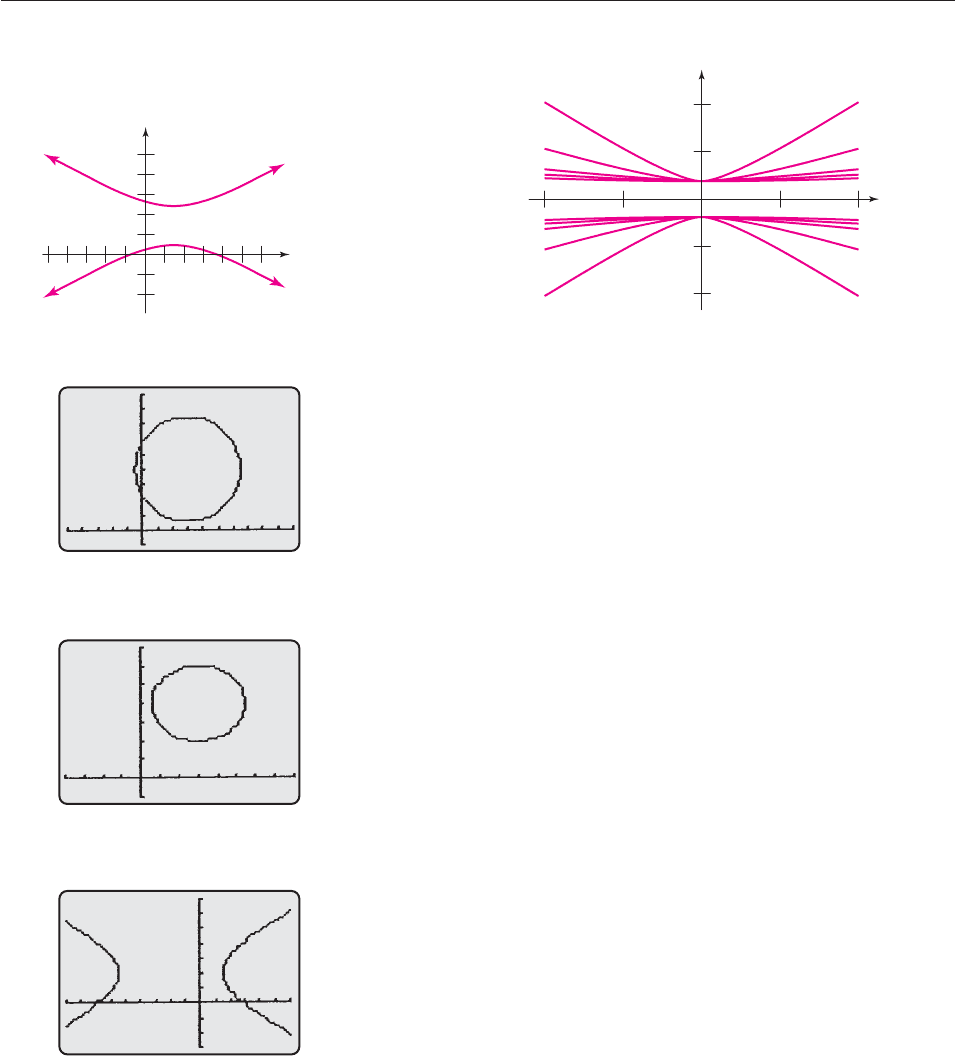
v
n
u
i
n
r(cos u i sin u)
1 r (cos u i sin u).
Thus, the vu
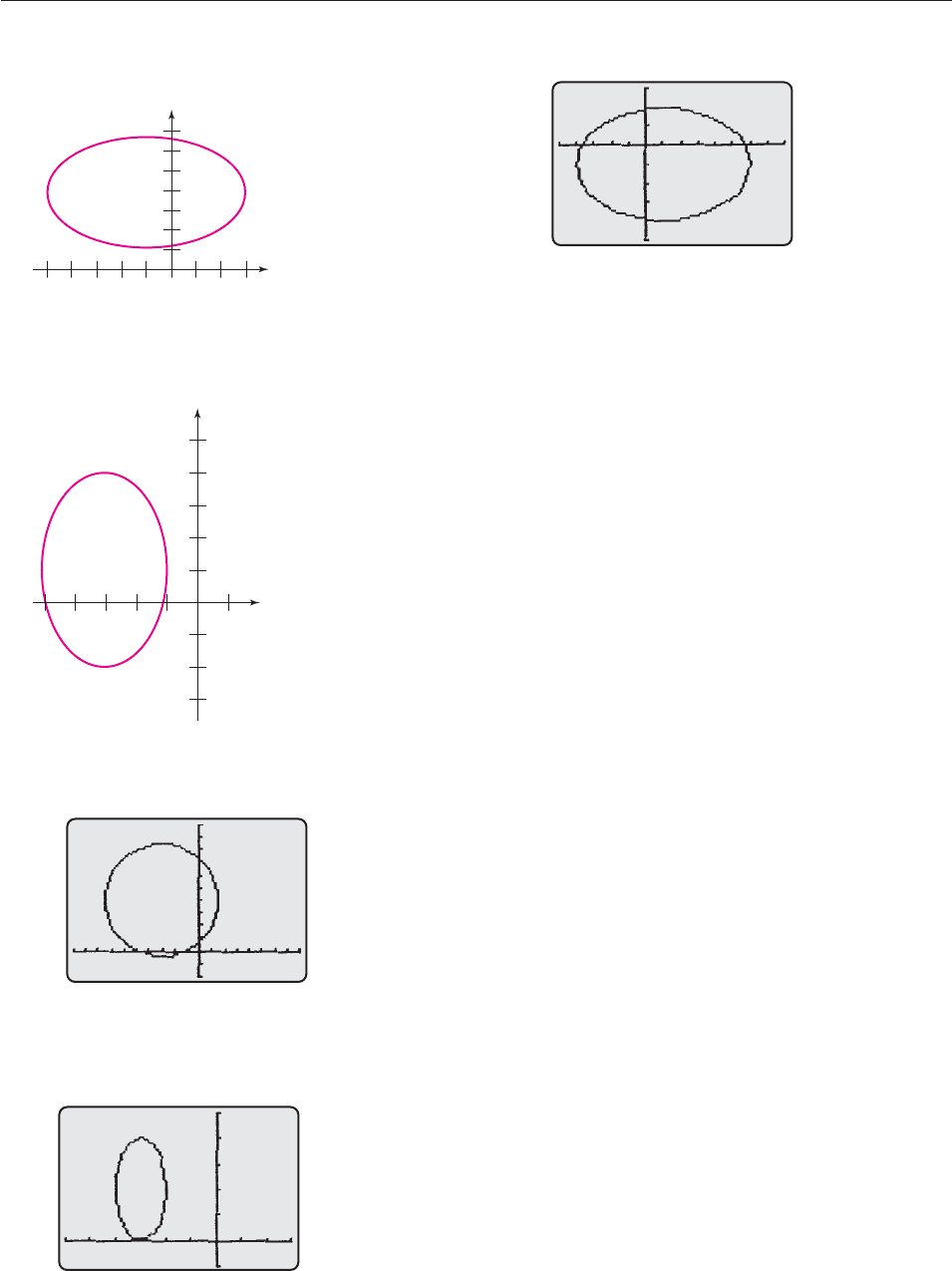
i
are the solutions of the equation.
Section 9.3, page 651
1. 35
3. 34
5. 6, 6 7. 6, 10
9. 13/5, 2/5
11. u v 4, 5; v u 8, 3; 2u 3v 22, 5
13. u v 3 42
, 32
1;
v u
42
3, 1 32
;
2u 3v
6 122
, 62
3
15. u v 23/4, 13; v u 9/4, 7;
2u 3v 11/4, 11
17. u v 14i 4j; v u 2i 4j; 2u 3v 2i 12j
19. u v
5
4
i
3
2
j; v u
1
4
1
i
3
2
j;
2u 3v
4
25
i 3j
21. 7, 0 23. 2, 1/2
25. 6, 13/4 27. 4, 0
29. 52
, 52
31. 4.5963, 3.8567
33. .1710, .4698 35. v 42
, u 45°
37. v 8, u 180° 39. v 6, u 90°
41. v 217, u 104.04°
43.
4
41
,
5
41
45.
1
5
,
2
5
47. u v 108.2 pounds, u 46.1°
49. u v 17.4356 newtons, u 213.4132°
51. 8, 2; v 8, 2
53. v 0 c, d 0, 0 c, d v and
0 v 0, 0 c, d c, d v
55. r(u v) r(a, b c, d) ra c, b d
ra rc, rb rd ra, rb rc, rd
ra, b rc, d ru rv
57. (rs)v rsc, d rsc, rsd rsc, sd r(sv) and
rsc, rsd src, srd src, rd s(rv)
59. 48.575 pounds
61. 32.1 pounds parallel to plane; 38.3 pounds perpendicular
to plane
63. 66.4°
1026 ANSWERS
65. Ground speed: 253.2 mph; course: 69.1°
67. Ground speed: 304.1 mph; course: 309.5°
69. Air speed: 424.3 mph; direction: 62.4°
71. 69.08°
73. 341.77 lb on v; 170.32 lb on u
75. 517.55 lb on the 28° rope; 579.90 lb on the 38° rope
77. (a) v x
2
x
1
, y
2
y
1
; kv kx
2
kx
1
, ky
2
ky
1
(b) v
(x
2
x
1
)
2
(y
2
y
1
)
2
kv
(kx
2
kx
1
)
2
(ky
2
ky
1
)
2
(c) kv
k
2
(x
2
x
1
)
2
k
2
(y
2
y
1
)
2
k
2
(x
2
x
1
)
2
(y
2
y
1
)
2
k
(x
2
x
1
)
2
(y
2
y
1
)
2
k v
(d) tan u
y
x
2
2
y
x
1
1
k
k
y
x
2
2
y
x
1
1
k
k
y
x
2
2
k
k
y
x
1
1
tan b
Since the angles have the same tangent, they can differ
only by a multiple of p and so are parallel. They have
either the same or the opposite direction.
(e) If k 0, the signs of the components of kv are the same
as those of v, so the two vectors lie in the same quad-
rant. Therefore, they must have the same direction. If
k 0, then the components of kv and the components of
v must have opposite signs, and the two vectors do not
lie in the same quadrant. Therefore, they do not have the
same direction and must have opposite directions.
79. (a) Since u v a c, b d, u v
(a c
)
2
(b
d)
2
. The magnitude of w is given
by the distance between the points (a, b) and (c, d ).
Hence, u v w.
(b) u v lies on the straight line through (0, 0) and
(a c, b d ), which has slope
(
(
b
a
d
c)
)
0
0
b
a
d
c
. w lies on the line joining
(a, b) and (c, d). This also has slope
b
a
d
c
. Since
the slopes are the same, the vectors, u v and w are par-
allel. Therefore, they either point in the same direction or
in opposite directions. We can see that they have the
same direction by considering the signs of the compo-
nents of u v. If a c 0 and b d 0, then a c,
b d and u v and w both point up and right. If
a c 0 and b d 0, both vectors will point left and
up. If a c 0 and b d 0, both vectors will point left
and down. In any case, they point in the same direction.
Section 9.4, page 661
1. u
v 7, u
u 25, v
v 29
3. u
v 6, u
u 5, v
v 9
5. u
v 12, u
u 13, v
v 13
7. 1 9. 6
11. 34 13. 1.75065 radians
15. 2.1588 radians 17. p/2 radians

19. Orthogonal 21. Parallel
23. Neither 25. k 2
27. k 2
29. proj
u
v 12/17, 20/17; proj
v
u 6/5, 2/5
31. proj
u
v 0, 0; proj
v
u 0, 0
33. comp
v
u 22/13 35. comp
v
u 3/10
37. u
(v w) a, b
(c, d r, s)
a, b
c r, d s a(c r) b(d s)
ac ar bd bs
u
v u
w a, b
c, d a, b
r, s
(ac bd ) (ar bs) ac ar bd bs
39. 0
u 0, 0
a, b 0a 0b 0
41. If u 0 or p, then u and v are parallel, so v ku for some
real number k. We know that v k u (Exercise 77, Sec-
tion 9.3). If u 0, then cos u 1 and k 0. Since k 0,
k k and so v ku. Therefore, u
v u
ku
ku
u ku
2
u(ku) uv uv cos u. On the
other hand, if u p, then cos u 1 and k 0. Since k 0,
k k and so v ku. Then u
v u
ku
ku
u ku
2
u(ku) uv uv cos u. In
both cases we have shown u
v uv cos u.
43. If A (1, 2), B (3, 4), and C (5, 2), then the vector
AB
2, 2, AC
4, 0, and BC
2, 2. Since
AB
BC
0, AB
and BC
are perpendicular, so the angle
at vertex B is a right angle.
45. Many possible answers: One is u 1, 0, v 1, 1, and
w 1, 1.
47. 300 lb ( 600 sin 30°) 49. 13
51. 24
53. The force in the direction of the lawnmower’s motion is
30 cos 60° 15 lb. Thus, the work done is
15(75) 1125 ft-lb.
55. 1368 ft-lb
Chapter 9 Review, page 664
1. 20 10
3.
y
1
x
ANSWERS 1027
5. 2
cos
p
3
i sin
p
3
7. 42
42
i
9. 23
2i 11.
8
2
1
81
2
3
i
13. cos 0 i sin 0, cos
p
3
i sin
p
3
, cos
2
3
p
i sin
2
3
p
,
cos p i sin p, cos
4
3
p
i sin
4
3
p
, cos
5
3
p
i sin
5
3
p
15. cos
p
8
i sin
p
8
, cos
5
8
p
i sin
5
8
p
, cos
9
8
p
i sin
9
8
p
,
cos
13
8
p
i sin
13
8
p
17. 8, 4 19. 105
21. 14, 9
23. 17 25. 52
/2, 52
/2
27.
i
j
29. Ground speed: 321.87 mph; course: 126.18°
31. 22 33. 15 35. .70 radians
37. proj
v
u v 2i j
39. (u v)
(u v) u
u u
v v
u v
v
u
u v
v u
2
v
2
0 since u and v have the
same magnitude.
41. 1750 lb
Chapter 9 Test, page 665
1.
2. 5832i 3. 13
4. 4
cos
4
p
8
i sin
4
p
8
, 4
cos
1
1
1
6
p
i sin
1
1
1
6
p
,
4
cos
6
4
5
8
p
i sin
6
4
5
8
p
5. (a) 34 (b) 34
6.
3
2
cos
p
9
i sin
p
9
,
3
2
cos
7
9
p
i sin
7
9
p
,
3
2
cos
13
9
p
i sin
13
9
p
x
y
5
(3, 9)
5
5
5
2
5
1
5
7.
8.
cos
3
8
p
i sin
3
8
p
, cos
7
8
p
i sin
7
8
p
,
cos
11
8
p
i sin
11
8
p
, cos
15
8
p
i sin
15
8
p
9. 39i
10. 33
3i, 3 33
i, 33
i 3i, 3 33
i
11. 5
cos
4
3
p
i sin
4
3
p
12. 1, i, i
13. 7, 13 14. 86
15. 11 i 5
j, 11 i 5
j, 511 i 65
j
16. 1.8925 17.
3
2
3
,
3
2
18.
2
7
19.
7
85
i
6
85
j 20.
1
1
0
0
21. (a) 3, 11 (b) 3, 11
22. 42 23. 1.01 24. 3194.95 ft-lb
Chapter 10
Section 10.1, page 683
1. x
2
( y 3)
2
4 3. x
2
6y
2
18
5. (x 4)
2
( y 3)
2
4
7. Center (4, 3), radius 210
9. Center (3, 2), radius 27
11. Center (25/2, 5), radius
6
2
77
13.01
13. ellipse; center (0, 0); vertices (5, 0), 5, 0);
foci (21, 0), (21, 0)
2
2
4
4
2
6
6
4646 2
x
y
2468
−8 −6 −4 −2
2
4
6
8
−4
−6
−8
x
y
1028 ANSWERS
15. ellipse; center (0, 0), vertices (0, 2), (0, 2); foci (0, 1),
(0, 1)
17. ellipse; center (0, 0); vertices (9, 0), (9, 0);
foci (32, 0), (32, 0)
19. circle; center (0, 0); radius 1/2
21.
4
x
9
2
y
4
2
1 23.
3
x
6
2
1
y
6
2
1
25.
x
9
2
4
y
9
2
1 27. 8p
29. 2p3
31. 7p/3
33. ellipse; center (1, 5); vertices (1, 2), (1, 8);
foci (0, 5
5), (0, 5
5)
2
2
4
1
5
3
6
8
9
7
1
431545 2 13
x
y
1
1
2
2
1
22 1
x
y
2
2
4
4
2
6
10
8
6
10
8
46 10846108 2
x
y
2
2
4
3
4
2
1
5
3
1
5
431545 2 13
x
y
35. Ellipse, center (1, 4); vertices (5, 4), (3, 4);
foci (22
1, 4), (22
1, 4)
37. Ellipse, center (3, 1); vertices (3, 4), (3, 2);
foci (3, 5
1), (3, 5
1)
39. circle; center (3, 4)
41. ellipse; center (3, 2)
5
6
1
3
10
10
2
8
1
−1
−2
−3
2
3
4
5
x
y
−11−2−3−4−5
10
3
4
1
2
5
6
7
x
y
−1−2−3−4−5
23
ANSWERS 1029
43. ellipse; center (1, 1)
45.
(x
4
2)
2
( y
16
3)
2
1
47.
(x
2
5/
7
4
)
2
( y
36
4)
2
1
49.
(x
36
3)
2
( y
16
2)
2
1
51.
(x
49
5)
2
( y
16
3)
2
1 or
(x
16
5)
2
( y
49
3)
2
1
53. 2x
2
2y
2
8 0
55. 2x
2
y
2
8x 6y 9 0
57.
(x
4
3)
2
(y
8
3)
2
1
59. The ellipse has y-intercepts (0, 4). Therefore, the circle,
which has center at the origin, has radius 4. The equation of
the circle must be x
2
y
2
16.
61. The minimum distance is 226,335 miles. The maximum dis-
tance is 251,401 miles.
63. 80 ft 65. 17.3 ft
67. Eccentricity .1
69. Eccentricity
2
3
.87
71. The closer the eccentricity is to zero, the more the ellipse re-
sembles a circle. The closer the eccentricity is to 1, the more
elongated the ellipse becomes.
73. Eccentricity .38.
75. If a b, the equation becomes
x
a
2
2
y
a
2
2
1,
x
2
y
2
a
2
.
This is the equation of a circle with center at the origin,
radius a.
77. The fence is an ellipse with major axis 100 ft, minor axis
503
86.6 ft.
Section 10.2, page 697
1. x
2
4y
2
1
3. 2x
2
y
2
8
5. 6x
2
2y
2
18
3
5
5
8
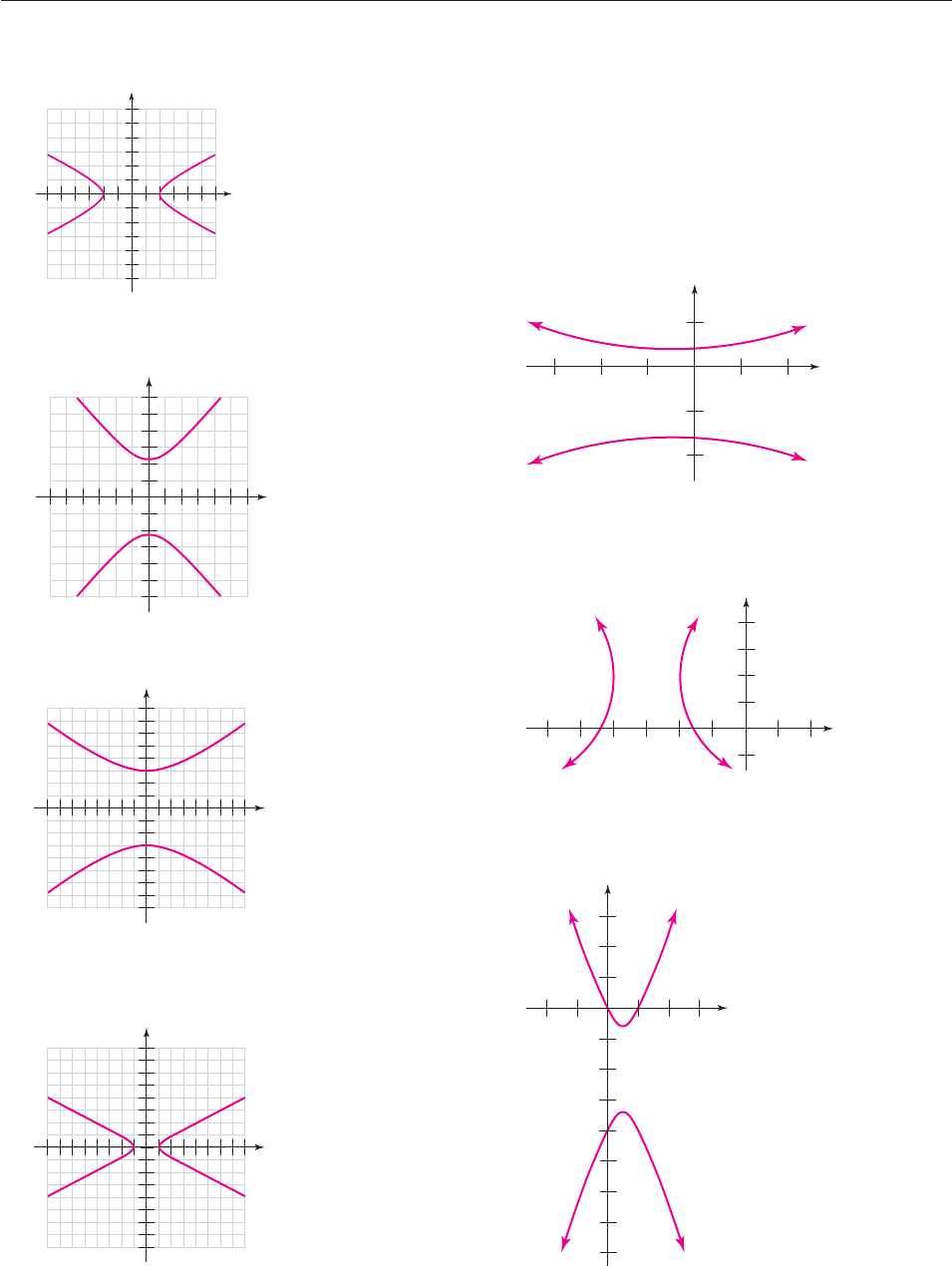
7. hyperbola; vertices (2, 0), (2, 0);
foci (5
, 0), (5
, 0); asymptotes y
1
2
x
9. hyperbola; vertices (0, 5
), (0, 5
);
foci (0, 8
), (0, 8
); asymptotes y
5
3
x
11. hyperbola; vertices (0, 3), (0, 3);
foci (0, 5), (0, 5); asymptotes y
3
4
x
13. hyperbola; vertices (1, 0), (1, 0);
foci
2
5
, 0
,
2
5
, 0
; asymptotes y
1
2
x
2
2
4
4
2
6
8
6
8
468468 2
x
y
2
2
4
4
2
6
8
6
8
468468 2
x
y
2
2
4
4
2
6
6
4646 2
x
y
2
2
4
4
2
6
6
4646 2
x
y
1030 ANSWERS
15.
x
4
2
1
y
6
2
1 17.
2
y
5
2
x
4
2
1
19.
(x
9
2)
2
(y
4
1)
2
1 21.
x
9
2
3
y
6
2
1
23.
x
4
2
y
1
2
1
25. Hyperbola, center (1, 3); vertices (1, 8), (1, 2);
foci (1, 3 41), (1, 3 41); asymptotes
y 3
5
4
(x 1)
27. Hyperbola, center (3, 2); vertices (4, 2), (2, 2);
foci (3 5
, 2), (3 5
, 2);
asymptotes y 2 2(x 3)
29. Hyperbola, center (1, 4); vertices (1,4 8
),
(1, 4 8
); foci (1, 7), (1, 1); asymptotes
y 4 8
(x 1)
6
4
2
−4
−2
−6
−8
x
y
2−2−44
6
−10
−12
−14
−16
2
1
4
3
−1
x
y
−1−2−3−4−5−612
−10
−5
5
x
y
−2−4−624
31. Hyperbola, center (3, 3); vertices (3, 1),(3, 5);
foci (3, 320), (3, 320); asymptotes
y 3
1
2
(x 3)
33. circle; center (3, 4)
35. ellipse; center (3, 4)
37. hyperbola; center (2, 2)
39.
(y
4
3)
2
(x
6
2)
2
1
41.
(x
9
4)
2
( y
16
2)
2
1
43. y
2
2x
2
6 45.
( y
4
2)
2
(x
9
3)
2
1
47.
(x
3
3)
2
(y
4
3)
2
1
7
9
3
6
7
4
1
8
9
5
1
10
6
8
2
4
−4
10
x
y
810
12
2−2−4−6−8−10 4 6
ANSWERS 1031
49. The graphs are shown below on one set of coordinate axes.
As b increases, the graphs get flatter. Although the hyper-
bola may look like two horizontal lines for very large b, it is
still a hyperbola, with asymptotes y 2x/b that have
nonzero slopes.
51. The asymptotes of
x
a
2
2
y
a
2
2
1 are y
a
a
x or y x.
Since they have slopes 1 and 1 and 1(1) 1, they are
perpendicular.
53. The equation is
1,21
x
0
2
,000
5,75
y
9
2
,600
1 (measurement
in feet). The exact location cannot be determined from only
the given information.
55.
2
x
5
2
1
2
6
2
y
5
2
1 57. 5
2.24
59. 3
61. 3/2
Section 10.3, page 710
1. 6x y
2
3. 2x
2
y
2
8 5. x
2
6y
2
18
7. y
2
16x 9. x
2
32y
11. Focus: (0, 1/12), directrix y 1/12
13. Focus: (0, 1), directrix y 1
15. Focus: (2, 0), directrix x 2
17. Opens to the right.
Vertex: (2, 0), focus: (9/4, 0), directrix: x 7/4
19. Opens to the left.
Vertex: (2, 1), focus: (7/4, 1), directrix: x 9/4
21. Opens to the right.
Vertex: (2/3, 3), focus: (17/12, 3), directrix: x 1/12
23. Opens to right.
Vertex: (81/4, 9/2), focus: (20, 9/2), directrix:
x 41/2
25. Opens upward.
Vertex: (1/6, 49/12), focus: (1/6, 4), directrix:
y 25/6
27. Opens downward.
Vertex: (2/3, 19/3), focus: (2/3, 25/4), directrix: y 77/12
−5
−10
5
10
x
y
−5−10 5 10
29. Line segment from (4, 2) to (4, 2)
31. Line segment from (5, 10) to (5, 10)
33. Line segment from (2, 1) to (2, 1)
35.
37.
39.
41.
43.
y 3x
2
45. y 13(x 1)
2
47. x 2 3( y 1)
2
49. x 3 4(y 2)
2
2
1
4
5
3
−1
−2
x
y
−1−2−3−4−5123
(−1, 1)
−2
−4
−6
2
4
x
y
−1−212345
(2, −5)
2
(0, 2)
4
2
5
3
1
−1
x
y
−2
46810
1
8
10
4
6
2
x
y
−2 −1
2345
(1, 2)
1032 ANSWERS
51. y 1 2(x 1)
2
53. (y 3)
2
x 1
55. Parabola, vertex (3, 4)
57. Parabola, vertex (2/3, 1/3)
59. Circle, center (1, 2)
61. Hyperbola, center (4, 2), vertices
4 2
, 2
63. y (x 4)
2
2 65. y x
2
8x 18
67. y (x 5)
2
3 69. b 0
71.
9,
1
2
34
73. (a) The focus is ( p, 0). To find the points on the parabola
directly above and below the focus, let x p and solve
y
2
4px for y: y
2
4p
2
, so that y 2p. Hence, the
endpoints are ( p, 2p) and (p, 2p).
(b) The focus is (0, p). Let y p and solve x
2
4py for x.
Then x 2p and the endpoints are (2p, p) and (2p, p).
75. The receiver should be placed at the focus,
2
3
ft or 8 in from
the vertex.
77. 43.3 ft 79. 5.072 meters 81. 27.44 ft
4
2
−2
−4
8
6
x
y
−22−4−6−8−10
2
1
4
3
x
y
1−123
2
3
1
−1
−2
x
y
246
810
4
2
−2
−4
−6
x
y
246
Special Topics 10.3.A, page 717
1. x 5 cos t and y 5 sin t (0 t 2)
3. x 3 cos t 4 and y 3 sin t ⫺2 (0 t 2)
5. x 5
cos t 1 and y 5
sin t (0 t 2)
7. x 10 cos t and y 6 sin t (0 t 2p)
9. x
1
2
cos t and y
1
2
sin t (0 t 2p)
−2
2
−33
−7
7
−10 10
3.1
4.7
3.1
4.7
2
3
6
9
6
9
6
9
ANSWERS 1033
11. x 2 cos t 1, y 3 sin t 5(0 t 2p)
13. x 4 cos t 1, y 8
sin t 4(0 t 2p)
15. x 10/cos t and y 6 tan t (0 t 2p)
17. x 1/cos t and y
1
2
tan t (0 t 2p)
19. x 4 tan t 1, y 5/cos t 3(0 t 2p)
−15
−18
18
9
−4
4
−66
−10
10
−10 10
−1
−7
7
9
−1
−5
10
9
21. x 1/cos t 3, y 2 tan t 2(0 t 2p)
23. x t
2
/4, y t
25. x t, y 4(t 1)
2
2
27. x 2(t 2)
2
, y t
29. Circle; center (0, 5), radius 3
31. Ellipse; center (4, 0) 33. Hyperbola; center (2, 4)
35. Hyperbola; center (0, 3)
37. Parabola; vertex (4, 3)
39. (a) x
2
y
2
cos
2
(.5t) sin
2
(.5t) 1
(b) x
2
y
2
cos
2
(.5t) (sin(.5t))
2
cos
2
(.5t)
sin
2
(.5t) 1
(c) Since cos(.5t) and sin(.5t) each have period 4p, the
parametric equations trace out a half-circle when
0 t 2p.
−4
−2 10
6
−5
−9 11
15
−10
−5 15
10
−10
−10
10
10
1034 ANSWERS
There are many correct answers to Exercises 40–43, some of
which are shown here.
41. 43.
Section 10.4, page 722
1. Ellipse 3. Parabola
5. Hyperbola
7. Ellipse. Window 6 x 3 and 2 y 4.
9. Hyperbola. Window 7 x 13 and 3 y 9.
11. Parabola. Window 1 x 8 and 3 y 3.
13. Ellipse. Window 1.5 x 1.5 and 1 y 1.
15. Hyperbola. Window 15 x 15 and 10 y 10.
17. Parabola. Window 19 x 2 and 1 y 13.
19. Hyperbola. Window 15 x 15 and 15 y 15.
21. Ellipse. Window 6 x 6 and 4 y 4.
23. Parabola. Window 9 x 4 and 2 y 10.
Special Topics 10.4.A, page 727
1.
5
2
2
,
2
2
3.
2
3
,
1
2
5.
u
2
2
v
2
2
1
7.
u
4
2
v
2
1
9. u 53.13°; x
3
5
u
4
5
v; y
4
5
u
3
5
v
11. u 36.87°; x
4
5
u
3
5
v; y
3
5
u
4
5
v
13. (a) (A cos
2
u B cos u sin u C sin
2
u)u
2
(B cos
2
u
2A cos u sin u 2C cos u sin u B sin
2
u)uv
(C cos
2
u B cos u sin u A sin
2
u)v
2
(D cos u
E sin u)u (E cos u D sin u )v F 0
(b) BB cos
2
u 2A cos u sin u 2C cos u sin u
B sin
2
u 2(C A)sin u cos u B(cos
2
u sin
2
u)
since B is the coefficient of uv
(c) Since sin 2u 2 sin u cos u and cos 2u cos
2
u
sin
2
u, B(C A) sin 2u B cos 2u.
(d) If cot 2u
A
B
C
, then
c
s
o
in
s
2
2
u
u
A
B
C
, so that
B cos 2u (A C) sin 2u. Since (A C) C A,
we have: B(C A) sin 2u B cos u 0.
15. (a) From Exercise 13(a) we have (B)
2
4AC
(B cos
2
u 2A cos u sin u 2C cos u sin u
B sin
2
u)
2
4(A cos
2
u B cos u sin u
C sin
2
u)(C cos
2
u B cos u sin u Asin
2
u)
[B(cos
2
u sin
2
u) 2(C A) cos u sin u]
2
4(A cos
2
u B cos u sin u C sin
2
u )(C cos
2
u
B cos u sin u A sin
2
u) B
2
(cos
2
u sin
2
u)
2
4(C A)
2
cos
2
u sin
2
u 4B(C A)(cos
2
u
sin
2
u) cos u sin u [4AC(cos
4
u sin
4
u)
4(A
2
C
2
B
2
) cos
2
u sin
2
u 4AB(cos
3
u sin u
cos u sin
3
u ) 4BC(cos
3
u sin u cos u sin
3
u )]
B
2
(cos
4
u 2 cos
2
u sin
2
u sin
4
u 4 cos
2
u sin
2
u)
4AC(2 cos
2
u sin
2
u cos
4
u sin
4
u) (everything else
cancels) (B
2
4AC)(cos
4
u 2 cos
2
u sin
2
u
sin
4
u) (B
2
4AC)(cos
2
u sin
2
u)
2
B
2
4AC
(b) If B
2
4AC 0, then also (B)
2
4AC0. Since
B0, 4AC0 and so AC0. By Exercise 14,
the graph is an ellipse. The other two cases are proved
in the same way.
Section 10.5, page 738
1. 5 x 6 and 2 y 2
3. 3 x 4 and 2 y 3
5. 3 x 3 and 2 y 2
7. 5 x 4 and 4 y 5
9. 0 x 14 and 15 y 0
11. 2 x 20 and 11 y 11
13. 12 x 12 and 12 y 12
15. 2 x 20 and 20 y 4
17. 25 x 22 and 25 y 26
19. y 2x 7 21. y 2x 5
23. x y
3
y 25. y x
8
1
27. x e
y
(or y ln x) 29. x
2
y
2
9
31. Both give a straight line segment between P (4, 7) and
Q (2, 5). The parametric equations in (a) move from P
to Q, and the parametric equations in (b) move from Q to P.
33. x 6 cos t 7 and y 6 sin t 4(0 t 2p)
35. x 3 cos t 2 and y 3 sin t 2(0 t 2p)
37. x 5 cos t and y 18 sin t (0 t 2p)
39. x
co
3
s t
and y 15 tan t (0 t 2p)
41. x 24 tan t
5
and y
co
6
s t
2
(0 t 2p)
43. (a)
d
c
a
b
(b) y b
d
c
a
b
(x a)
(c) Solving both equations for t, we obtain t
x
c
a
a
and
t
d
y
b
b
.
Hence,
d
y
b
b
x
c
a
a
; that is,
y b
d
c
a
b
(x a).
ANSWERS 1035
45. x 18t 6 and y 12 22t (0 t 1)
47. x 18 34t and y 10t 4(0 t 1)
49. (a) k 1 k 2
k 3 k 4
(b) k 5 k 6
51. (a)–(d)
8
20
1
20
(b)
(c)(a)
(d)
−1.5
1.5
−1.5 1.5
−1.5
1.5
−1.5 1.5
−1.5
1.5
−1.5 1.5
−1.5
1.5
−1.5 1.5
−1.5
1.5
−1.5 1.5
−1.5
1.5
−1.5 1.5
0
18
−20 20
−12
14
−814
