Hull J.C. Risk management and Financial institutions

Подождите немного. Документ загружается.

260 Chapter 11

Define Q(t) as the probability of default by time t. It follows that

11.3 RECOVERY RATES

When a company goes bankrupt, those that are owed money by the

company file claims against the assets of the company.

Sometimes there

is a reorganization in which these creditors agree to a partial payment of

their claims. In other cases the assets are sold by the liquidator and the

proceeds are used to meet the claims as far as possible. Some claims

typically have priorities over other claims and are met more fully.

The recovery rate for a bond is normally defined as the bond's market

value immediately after a default as a percent of its face value. It equals one

minus the loss given default, LGD. Table 11.2 provides historical data on

average recovery rates for different categories of bonds in the United

States. It shows that senior secured debtholders had an average recovery

rate of 57.4 cents per dollar of face value, while junior subordinated

debtholders had an average recovery rate of only 28.9 cents per dollar of

face value.

Recovery rates are significantly negatively correlated with default rates.

Moody's looked at average recovery rates and average default rates each

Table 11.2 Recovery rates on corporate bonds as a

percent of face value, 1982-2004. Source: Moody's.

In the United States, the claim made by a bondholder is the bond's face value plus

accrued interest.

Class

Senior secured

Senior unsecured

Senior subordinated

Subordinated

Junior subordinated

Average recovery

rate (%)

57.4

44.9

39.1

32.0

28.9

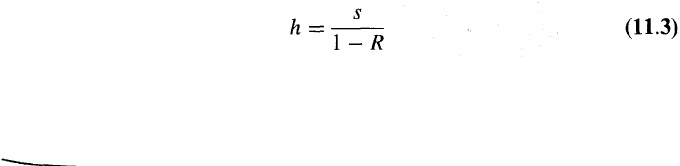
Credit Risk: Estimating Default Probabilities 261

year between 1983 and 2004. It found that the following relationship

provides a good fit to the data:

Average recovery rate = 0.52 — 6.9 x Average default rate

This relationship means that a bad year for the default rate is usually

doubly bad because it is accompanied by a low recovery rate. For

example, when the average default rate in a year is only 0.1%, we expect

the recovery rate to be relatively high at 51.3%. When it is relatively high

at 3%, we expect the recovery rate to be 31.3%.

11.4 ESTIMATING DEFAULT PROBABILITIES FROM

BOND PRICES

The probability of default for a company can be estimated from the prices

of bonds it has issued. The usual assumption is that the only reason a

corporate bond sells for less than a similar risk-free bond is the possibility

of default.

Consider first an approximate calculation. Suppose that a bond yields

200 basis points more than a similar risk-free bond and that the expected

recovery rate in the event of a default is 40%. The holder of a corporate

bond must be expecting to lose 200 basis points (or 2% per year) from

defaults. Given the recovery rate of 40%, this leads to an estimate of the

probability of a default per year conditional on no earlier default of

0.02/(1 - 0.4), or 3.33%. In general,

where h is the default intensity per year, s is the spread of the

corporate bond yield over the risk-free rate, and R is the expected

recovery rate.

See D. T. Hamilton, P. Varma, S. Ou, and R. Cantor, "Default and Recovery Rates of

Corporate Bond Issuers, 1920-2004," Moody's Investor's Services, January 2005. The R

of the regression is 0.65. The correlation is also identified and discussed in E. I. Altman,

B. Brady, A. Resti, and A. Sironi, "The Link between Default and Recovery Rates:

Implications for Credit Risk Models and Procyclicality," Working Paper, New York

University, 2003.

We discuss this point later. The assumption is not perfect. In practice, the price of a

corporate bond is also affected by its liquidity. The lower the liquidity, the lower the

price.

262 Chapter 11

A More Exact Calculation

For a more exact calculation, suppose that the corporate bond we have

been considering lasts for five years, provides a coupon of 6% per annum

(paid semiannually), and yields 7% per annum (with continuous com-

pounding). The yield on a similar default-free bond is 5% (with continuous

compounding). The yields imply that the price of the corporate bond is

95.34 and the price of the default-free bond is 104.09. The expected loss

from default over the five-year life of the bond is therefore 104.09 - 95.34,

or $8.75. Suppose that the probability of default per year (assumed in this

simple example to be the same each year) is Q. Table 11.3 calculates the

expected loss from default in terms of Q on the assumption that defaults

can happen at times 0.5, 1.5, 2.5, 3.5, and 4.5 years (immediately before

coupon payment dates). Risk-free rates for all maturities are assumed to

be 5% (with continuous compounding).

To illustrate the calculations, consider the 3.5-year row in Table 11.3.

The expected value of the default-free bond at time 3.5 years (calculated

using forward interest rates) is

Given the definition of recovery rates in the previous section, the amount

recovered if there is a default is 40, so that the loss is 104.34 - 40, or

$64.34. The present value of this loss is 54.01 and the expected loss is

therefore 54.01 Q.

The total expected loss is 288.48(2. Setting this equal to 8.75, we obtain a

value for Q equal to 3.03%. The calculations we have given assume that

Table 11.3 Calculation of loss from default on a bond in terms of the default

probabilities per year, Q. Notional principal = $100.

Time

(years)

0.5

1.5

2.5

3.5

4.5

Total

Default

probability

Recovery

amount

($)

Default-free

value ($)

106.73

105.97

105.17

104.34

103.46

Loss

($)

66.73

65.97

65.17

64.34

63.46

Discount

factor

0.9753

0.9277

0,8825

0.8395

0.7985

PV of

expectea

loss ($)

65.08Q

61.20Q

57.52Q

54.01Q

50.67Q

288.48Q

Credit Risk: Estimating Default Probabilities 263

the default probability is the same each year and that defaults take place

once a year. We can extend the calculations to assume that defaults can

take place more frequently. Furthermore, instead of assuming a constant

unconditional probability of default, we can assume a constant default

intensity or a particular pattern for the variation of default probabilities

with time.

With several bonds we can estimate several parameters describing the

term structure of default probabilities. Suppose, for example, we have

bonds maturing in 3, 5, 7, and 10 years. We could use the first bond to

estimate a default probability per year for the first three years, the second

to estimate a default probability per year for years 4 and 5, the third to

estimate a default probability for years 6 and 7, and the fourth to estimate

a default probability for years 8, 9, and 10 (see Problems 11.11 and

11.17). The approach is analogous to the bootstrap procedure we dis-

cussed in Chapter 4 for calculating a zero-coupon yield curve.

The Risk-Free Rate

A key issue when bond prices are used to estimate default probabilities is

the meaning of the terms "risk-free rate" and "risk-free bond". In equa-

tion (11.3) the spread s is the excess of the corporate bond yield over the

yield on a similar risk-free bond. In Table 11.3 the default-free value of the

bond must be calculated using risk-free rates. The benchmark risk-free rate

that is usually used in quoting corporate bond yields is the yield on similar

Treasury bonds (e.g., a bond trader might quote the yield on a particular

corporate bond as being a spread of 250 basis points over Treasuries).

As discussed in Section 4.4, traders usually use LIBOR/swap rates as

proxies for risk-free rates when valuing derivatives. Traders also use

LIBOR/swap rates as risk-free rates when calculating default probabil-

ities. For example, when they determine default probabilities from bond

Prices, the spread s in equation (11.3) is the spread of the bond yield over

the LIBOR/swap rate. Also, the risk-free discount rates used in the

calculations such as those in Table 11.3 are LIBOR/swap zero rates.

Credit default swaps (which will be discussed in Chapter 13) can be

used to imply the risk-free rate assumed by traders. The rate used appears

to be approximately equal to the LIBOR/swap rate minus 10 basis points

on average.

This estimate is plausible. As explained in Section 4.4, the

See J. Hull, M. Predescu, and A. White, "The Relationship between Credit Default

swap Spreads, Bond Yields, and Credit Rating Announcements," Journal of Banking and

Finance, 28 (November 2004), 2789-2811.

264 Chapter 11

credit risk in a swap rate is the credit risk from making a series of six-

month loans to AA-rated counterparties and 10 basis points is a reason-

able default risk premium for an AA-rated six-month instrument.

Asset Swaps

In practice, traders often use asset swap spreads as a way of extracting

default probabilities from bond prices. This is because asset swap spreads

provide a direct estimate of the spread of bond yields over the LIBOR/

swap curve.

To explain how asset swaps work, consider the situation where an asset

swap spread for a particular bond is quoted as 150 basis points. There are

three possible situations:

1. The bond sells for its par value of 100. The swap then involves one

side (Company A) paying the coupon on the bond and the other

side (Company B) paying LIBOR plus 150 basis points.

2. The bond sells below its par value, say, for 95. The swap is then

structured so that, in addition to the coupons, Company A pays $5

per $100 of notional principal at the outset.

3. The underlying bond sells above par, say, for 108. The swap is then

structured so that Company B makes a payment of $8 per $100 of

principal at the outset. After that, Company A pays the bond's

coupons and Company B pays LIBOR plus 150 basis points.

The effect of all this is that the present value of the asset swap spread is

the amount by which the price of the corporate bond is exceeded by the

price of a similar risk-free bond, where the risk-free rate is assumed to be

given by the LIBOR/swap curve (see Problem 11.12). Consider again the

example in Table 11.3 where the LIBOR/swap zero curve is flat at 5%.

Suppose that instead of knowing the bond's price we know that the asset

swap spread is 150 basis points. This means that the amount by which the

value of the risk-free bond exceeds the value of the corporate bond is the

present value of 150 basis points per year for five years. Assuming

semiannual payments, this is $6.55 per $100 of principal.

The total loss in Table 11.3 would be set equal to $6.55 in this case. This

means that the default probability per year, Q, would be 6.55/288.48,

or 2.27%.

Note that it is the promised coupons that are exchanged. The exchanges take place

regardless of whether the bond defaults.

Credit Risk: Estimating Default Probabilities 265

11.5 COMPARISON OF DEFAULT PROBABILITY

ESTIMATES

The default probabilities estimated from historical data are much less than

those derived from bond prices. Table 11.4 illustrates this.

It shows, for

companies that start with a particular rating, the seven-year average annual

default intensity calculated from (a) historical data and (b) bond prices.

The calculation of default intensities using historical data is based on

equation (11.2) and Table 11.1. From equation (11.2), we have

where is the average default intensity (or hazard rate) by time t

and Q(t) is the cumulative probability of default by time t. The values

of Q{1) are taken directly from Table 11.1. Consider, for example, an

A-rated company. The value of Q{7) is 0.0091. The average seven-year

default intensity is therefore

or 0.13%.

The calculations using bond prices are based on equation (11.3) and

bond yields published by Merrill Lynch. The results shown are averages

between December 1996 and July 2004. The recovery rate is assumed to be

40% and, for the reasons discussed in the previous section, the risk-free

interest rate is assumed to be the seven-year swap rate minus 10 basis

points. For example, for A-rated bonds the average Merrill Lynch yield was

Table 11.4 Seven-year average default intensities (% per annum).

Rating

Aaa

Baa

Caa

Historical default

intensity

0.04

0.06

0.13

0.47

2.40

7.49

16.90

Default intensity

from bonds

0.67

0.78

1.28

2.38

5.07

9.02

21.30

Ratio

16.8

13.0

9.8

5.1

2.1

1.2

1.3

Differeice

0.63

0.72

1.15

1.91

2.67

1.53

4.40

Tables 11.4 and 11.5 are taken from J. Hull, M. Predescu, and A. White, "Bond Prices,

Default Probabilities, and Risk Premiums," Journal of Credit Risk, 1, No. 2 (2004), 53-60.

266 Chapter 11

Table 11.5 Expected excess return on bonds (basis points).

Rating

Aaa

Baa

Caa

Bond yield

spread over

Treasuries

120

186

347

585

1321

Spread of risk-

free rate over

Treasuries

Spread for

historical

defaults

144

449

1014

Expected

excess

return

115

160

264

6.274%. The average swap rate was 5.605%, so that the average risk free

rate was 5.505%. This gives the average seven-year default probability as

or 1.28%.

Table 11.4 shows that the ratio of the default probability backed out of

bond prices to the default probability calculated from historical data is

high for investment-grade companies and tends to decline as the credit

quality declines. By contrast, the difference between the two default

probabilities tends to increase as credit quality declines.

Table 11.5 gives another way of looking at these results. It shows the

excess return over the risk-free rate (still assumed to be the seven-year swap

rate minus 10 basis points) earned by investors in bonds with different

credit ratings. Consider again an A-rated bond. The average spread over

Treasuries is 120 basis points. Of this, 43 basis points represent the average

spread between seven-year Treasuries and our proxy for the risk-free rate.

A spread of 8 basis points is necessary to cover expected defaults. (This

equals the real-world probability of default from Table 11.4 times 1 minus

the assumed recovery rate of 0.4.) This leaves an expected excess return

(after expected defaults have been taken into account) of 69 basis points.

Tables 11.4 and 11.5 show that a large percentage difference between

default probability estimates translates into a relatively small expected

excess return on the bond. For Aaa-rated bonds the ratio of the two

default probabilities is 16.8, but the expected excess return is only 38 basis

points. The expected return tends to increase as credit quality declines.

The results for B-rated bonds in Tables 11.4 and 11.5 run counter to the overall pattern.

Credit Risk: Estimating Default Probabilities 267

Interestingly, the excess return on bonds varies through time. It in-

creased steadily between 1997 and 2002 and then declined sharply in

2003 and 2004. For example, for the A-rated category the excess return

ranged from 35 basis points in 1997 to 119 basis points in 2002.

Real-World vs. Risk-Neutral Probabilities

The risk-neutral valuation argument is explained in Business Snap-

shot 11.1. It shows that we can value cash flows on the assumption that

all investors are risk neutral (i.e., on the assumption that they do not

require a premium for bearing risks). When we do this, we get the right

answer in the real world as well as in the risk-neutral world.

Business Snapshot 11.1 Risk-Neutral Valuation

The single most important idea in the valuation of derivatives is risk-neutral

valuation. It shows that we can value a derivative by

1. Assuming that all investors are risk neutral

2. Calculating expected cash flows

3. Discounting the cash flows at the risk-free rate

As a simple example of the application of risk-neutral valuation, suppose that

the price of a non-dividend-Paying stock is $30 and consider a derivative that

pays off $100 in one year if the stock price is greater than $40 at that time.

(This is known as a binary cash-or-nothing call option.) Suppose that the risk-

free rate (continuously compounded) is 5%, the expected return on the stock

(also continuously compounded) is 10%, and the stock price volatility is 30%

per annum. In a risk-neutral world the expected growth of the stock price is

5%. It can be shown (with the usual Black-Scholes lognormal assumptions)

that when the stock price has this growth rate the probability that the stock

price will be greater than $40 in one year is 0.1730. The expected payoff from

the derivatives is therefore 100 x 0.1730 = $17.30. The value of the derivative

is calculated by discounting this at 5%. It is $16.46.

The real-world (physical) probability of the stock price being greater than $40

in one year is calculated by assuming a growth rate of 10%. It is 0.2190. The

expected payoff in the real world is therefore $21.90. The problem with using

this expected cash flow is that we do not know the correct discount rate. The

stock price has risk associated with it that is priced by the market (otherwise the

expected return on the stock would not be 5% more than the risk-free rate). The

derivative has the effect of "leveraging this risk", so that a very high discount

rate is required for its expected payoff. Since we know the correct value of the

derivative is $16.46, we can deduce that the correct discount rate to apply to the

real-world expected payoff of $21.90 must be 28.6%.

268 Chapter 11

The default probabilities implied from bond yields are risk-neutral

default probabilities (i.e., they are the probabilities of default in a world

where all investors are risk neutral). To understand why this is so, consider

the calculations of default probabilities in Table 11.3. These assume that

expected default losses can be discounted at the risk-free rate. The risk-

neutral valuation principle shows that this is a valid procedure provided the

expected losses are calculated in a risk-neutral world. This means that the

default probability Q in Table 11.3 must be a risk-neutral probability.

By contrast, the default probabilities implied from historical data are

real-world default probabilities (sometimes also called physical probabil-

ities). The expected excess return in Table 11.5 arises directly from the

difference between real-world and risk-neutral default probabilities. If

there was no expected excess return, the real-world and risk-neutral

default probabilities would be the same, and vice versa.

Reasons for the Difference

Why do we see such big differences between real-world and risk-neutral

default probabilities? As we have just argued, this is the same as asking

why corporate bond traders earn more than the risk-free rate on average.

There are a number of potential reasons:

1. Corporate bonds are relatively illiquid and bond traders demand an

extra return to compensate for this. This may account for perhaps

25 basis points of the excess return. This is a significant part of the

excess return for high-quality bonds, but a relatively small part for

bonds rated Baa and below.

2. The subjective default probabilities of bond traders may be much

higher than the those given in Table 11.1. Bond traders may be

allowing for depression scenarios much worse than anything seen

during the 1970 to 2003 period. To test this, we can look at a table

produced by Moody's that is similar to Table 11.1, but applies to the

1920 to 2003 period instead of 1970 to 2003 period. When the

analysis is based on this table, historical default intensities for

investment-grade bonds in Table 11.4 rise somewhat. The Aaa

default intensity increases from 4 to 6 basis points; the Aa increases

from 6 to 22 basis points; the A increases from 13 to 29 basis points,

the Baa increases from 47 to 73 basis points. However, non-

investment-grade historical default intensities decline somewhat.

3. Bonds do not default independently of each other. This is the most

important reason for the results in Tables 11.4 and 11.5. There are

Credit Risk: Estimating Default Probabilities 269

periods of time when default rates are very low and periods of time

when they are very high. (Evidence for this can be obtained by

looking at the defaults rates in different years. Moody's statistics

show that between 1970 and 2003 the default rate per year ranged

from a low of 0.09% in 1979 to a high of 3.81% in 2001.) This gives

rise to systematic risk (i.e., risk that cannot be diversified away) and

bond traders should require an expected excess return for bearing the

risk. The variation in default rates from year to year may be because

of overall economic conditions or because a default by one company

has a ripple effect resulting in defaults by other companies. (The latter

is referred to by researchers as credit contagion.)

4. Bond returns are highly skewed with limited upside. As a result it is

much more difficult to diversify risks in a bond portfolio than in an

equity portfolio.

A very large number of different bonds must be

held. In practice, many bond portfolios are far from fully diversified.

As a result bond traders may require an extra return for bearing

unsystematic risk as well as for bearing the systematic risk mentioned

in 3 above.

Which Estimates Should Be Used?

At this stage it is natural to ask whether we should use real-world or risk-

neutral default probabilities in the analysis of credit risk. The answer

depends on the purpose of the analysis. When valuing credit derivatives

or estimating the impact of default risk on the pricing of instruments, we

should use risk-neutral default probabilities. This is because the analysis

calculates the present value of expected future cash flows and almost

invariably (implicitly or explicitly) involves using risk-neutral valuation.

When carrying out scenario analyses to calculate potential future losses

from defaults, we should use real-world default probabilities. The PD

used to calculate regulatory capital is a real-world default probability.

11.6 USING EQUITY PRICES TO ESTIMATE DEFAULT

PROBABILITIES

When we use a table such as Table 11.1 to estimate a company's real-

world probability of default, we are relying on the company's credit

See J. D. Amato and E. M. Remolona, "The Credit Spread Puzzle," BIS Quarterly

Review, 5 (December 2003), 51-63.