Hua C., Wong R. Differential Equations and Asymptotic Theory in Mathematical Physics
Подождите немного. Документ загружается.


72
in the direction
Rf,
we get
dt.
More generally, the integral
e-t/x
Ll+t
dt
exists if
d
#
lR-
and defines the sum
fd
in the direction
d.
\
Fig
1.5.4
The sum
fd
is defined in a disc (cf. Fig
1.5.4)
and Gevrey
1
asymptotic
to
f^
in every subsector of this disc. When we move
d,
the holomorphic
functions
fd
glue together analytically and define an holomorphic function
f^
on an eye-shaped %ector” whose opening is
3~
(-T
<
argx
<
T);
?is
asymptotic to
f^
on this %ector” in Gevrey
1
sense.
We denote
d
=
eieR+.
The allowed summation directions correspond
to
B
E]
-
T,
T[.
The function is multivalued: it has only one value
f
on
Re
x
>
0)
and two values
f+, f
-
on {Rex
<
0).
The “branches”
f
+
and
f
-
correspond respectively to
fdt
and
fd-
where
d+
=
eie+R+,
d-
=
eie-
R+
,
B+
=
T
+
a,
0-
=
T
-
a,
where
a
>
0
is “small”.
We can easily compare
f+
and
f-:
We can LLdeform”
y
in a bounded contour
y‘
without changing the integral
(Cauchy theorem and elementary estimates). Then we get
e-t/x
l+t
dt
=
2i7r
Res(-;
t
=
-1)
=
2he1/”

73
So,
f-(x)
-
f+(x)
=
2i7re1/"
which is,.as we waited, exponentially small on
the half-plane {Rex
<
0)
:
f-
-
f+
E
dS-l({Rex
<
0)).
The functions
f,
f,
f
+,
f
-
are
actual
solutions of the linear
non homogeneous
differential
equation (Euler equation):
2yl+ y
=
x.
The function
f-(x)
-
f+(x)
=
2i7re1/"
is an actual solution of the corre-
sponding
homogeneous
differential equation:
x2yl+ y
=
0.
We can now describe the
monodromy
of the problem, that is what hap-
pens to the solutions when we turn around the origin by
analytic continu-
ation.
We start from
f
on {Rex
>
0)
and we extend it by analytic continuation
along a loop turning around
0
in the positive sense (we replace
R+
=
eioR+
by
d
=
eieRf
with
8
~]O,7r[);
firstly we get
f-.
When
d
crosses
R-
(8
crosses
7r),
f-
jumps
to
f+
=
f-
-
2ire'l".
Therefore in this region
f+
+
2i7re1/"
is the analytic continuation of
f.
It
works for
Of
E]
-
7r,
O[.
Then we get an
extremely important
phenomena (an example of the Stokes
phenomena): near the direction
R-
(the singular direction of
f
:
C(f)
=
{It-}),
the two functions
ff
and
f-
admit the
same asymptotics (i.e.
f);
they differ by
2ine1/"
which is
infinitely flat.
The function
ff
+
2i7re1/"
admits the asymptotics
f
on
{Rex
<
0),
but
when we cross the line
-iR+
=
ePiT/'R+,
ff
keeps the same Asymptotics
f
and
2i7re1lX
jumps, turning
its asymptotics
(i.e.
0),
and becomes infinitely big (exponentially big) on
{Rex
>
0).
On the line
-iR+
it is bounded and
oscillates.
The line
-iRf
is
(I
think
improperly12)
named
Stokes line
by many authors. Turning
backwards we get a similar phenomena on the other Stokes line:
iR+
=
After one turn around the origin (in the positive sense) by
analytic
continuation,
the function
f
is
replaced
by the function
f
+
2i7re1/"
(it is
an
afine
transformation in the affine space of solutions of Euler ordinary
differential equation). We observe that
f
+
2i7re1/"
is
not asymptotic
to
f.
Its
dominant
part is
2i7re1/"
which exposes when
x
-+
0
in the half plane
{Rex
>
0).
ei.rr/ZR+.
I2The true Stokes phenomena happens when we cross the
singular
line
R-.
At the
beginning we cannot notice it by asymptotics and we observe it only when we cross
-iE%+.

74
Airy equation
(cf. [17]) This second example is the description of the
solutions of Airy equation
y“
-
zy
=
0
(1)
near
z
=
00,
using asymptotics. Stokes discovered Stokes phenomena study-
ing these solutions.
We consider Airy ordinary differential equation on the Riemann sphere
P’(C)
=
Cu
{co}.
Its
only singular
point on this Riemann sphere is clearly
z
=
co.
A first consequence is that any solution on a small disc centered at
zo
E
C
extends analytically to all
C:
it is
uniform
(single valued) and if we
turn around
co
along a loop by analytic continuation, we will go back to
the
same solution:
the (actual)
monodromy
transformation is the
identity.
Airy ordinary differential equation (1.5.1) admits
a
basis of
convergent
power series solutions at
z
=
0
(cf. 1.2). The sums of these series are
entire
functions(they are holomorphic on
C”).
We recall
We introduce the power series expansion
A(z)
=
c
.,(-.)-?
n20
where
r(n
+
;)r(n
+
i)
3
(-),
(n
E
N’);
cx,
=
1.
4
c,
=
n!
Let
t
=
z?
with
v
E
N’.
We set, by definition,
@[[t]ls
=
C[[z+]ls.
If
f^
E
C[[z+]ls,
we will say that it is of order
vs
in
2
in
a
generalized sense.
Theorem
1.6.
(i) The power series
A(,)
E
C[[z-i]]
is Gevrey of order
5
in
$
and g-summable
(in
$)
or
3-summable
in
t
(=
2-3)
in
every direction
except
argt
=
-IT
or
&:
(mod.
27~).
(ii) The sum
of
4z-1/4e-2/3r3’2~(z)
in
the direction
R+
is equal to
the classical Airy function Ai(z).
4rr
2
We set
B(z)
=
Cn>o~n~-%
=
A(-.).
Then
--1/4e2/3z3/2
AM,
z
z-1/4e-2/3z3/2

75
form a formal system of fundamental solutions of Airy ordinary differential
equation at
z
=
00.
By %-summation in
a
general
(i.e.
non singular)
direction we get
a
system of actual fundamental solutions. The jumps when
we move the direction correspond to Stokes phenomena (cf.
2.1
below)
2.
Applications
to
ordinary differential
equations
2.1.
Linear ordinary differential equations, index theorem
and Newton polygons
We will study in this part spaces of solutions
of
linear analytic differential
equations. We will give only the main results (for detailed proofs, cf.
[25],
[261)
*
The situation is local and we are interested in solutions of an operator
D
=
a,(x)(z)m
+ +
ao(x)
(where
ao,...
,a,
E
C{x})
in some
(topological) vector spaces. An important result
is
the finiteness
of
the
dimension of a solution space. Traditionally we can try to compute this
dimension using a fixed point method. This is elementary but it can be
technically difficult. Here we will use a different approach based on finite
index operators (Fredholm Operators). It is less precise: it gives
a
lower
estimate of the dimension (and not in general the dimension itself), but it is
very easy to apply (due in particular to stability by compact perturbations).
d
Definition
2.1.
Let
E,
F
be two complex vector spaces. A linear map u
:
E
4
F
has
a
finite index
x(u)
if dimc ker u and dimc cokeru
=
dimc F/imu
are finite. Then x(u)
=
dim ker u
-
dim coker u.
Example
2.1.
D
=
x
:
@“XI]
+
@“x]],
x(x)
=
-1;
d
d
dx
dx
D
=
-
:
@“x]]
4
@“XI],
x(-)
=
1.
Proposition
2.1.
Let
E,
F,
G
three complex vector spaces and
u
:
E
+
F,
v
:
F
4
G
two linear operators. We suppose that
u
and
v
have
a
finite index. Then the operator
v
o
u
:
E
+
F
has
also
a
finite index and
x(v
O
u>
=
x(v>
+
x(u>.
Example
2.2.
d.
x(xqZ)z)
=
i
-
d.
3
-)%
:
@“x]]
4
@[[XI].
x’(dx

76
Lemma
2.1.
(F. Riesz) Let
E
be a complex Banach space. Let
K
E
L(E,
E)
be a compact linear endomorphism ofE. Then the operatoridE+K
is a finite index endomorphism
of
E
and X(idE
+
K)
=
0.
Theorem
2.1.
Let
E,
F
be two complex Banach spaces. Let
K
E
L(E,
F)
be a compact operator. Let
u
:
E
-+
F be a continuous operator admitting a
finite index. Then
u+
K
E
L(E,
F)
has a finite index and
x(u+K)
=
~(u).
Be
careful:
In general
dim
ker(u
+
K)
#
dim
ker
u.
Lemma
2.2.
Let
El,
F1
and
E2,
Fz
be Banach spaces or Fre'chet spaces,
or DFS spaces(l) (same type
for
each pair,
but
the two pairs are allowed to
admit diflerent types
)I3.
If
we have a commutative diagram
where
u1,
u2,
v,
w
are linear continuous maps,
u1
are finite index maps,
v
and
w
are injective and
w
is dense, then:
(i)
We have an exact sequence
-
0
-+
kerp2
-+
EZ/E1
3
F2/Fl
and
ker
uz
has finite dimension with
dim ker
fiz
=
~(7~2)
-
x(u1).
This
im-
(ii) The pair
(v,
w)
is a quasi-isomorphism (i.e.
it
induces isomorphisms
plies
X(UZ)
2
x(u1).
on the kernels and colcernels oful and
u2
)
if
and only
if
x(u1)
=
~(uz).
This lemma generalizes some results of Dieudonnk and Schwartz and
was communicated to the author by
B.
Malgrange.
We will now explain how to compute indices of a differential operator
D
using the Newton polygon
N(D)
of
D.
The Newton polygon in this form is
due to the author
[26].
(There are a lot of Newton polygons associated to
differential equations are more general functional equations in the literature:
Fine, Adams, Komatsu
. . .
)
Let
D
=
a,(-&),
+
.
a
+
a.
be a holomorphic
(or
meromorphic
)
lin-
ear differential operator:
ao,
e.
'a,
E
C{x}
(or
C{x}[x-']).
We write the
13DFS
spaces are dual
of
FS
(
FrBchet Schwartz) spaces or equivalently
DF
spaces
of
Schwartz type.
77
expansion of
ai(x)
at
the origin:
aij
E
C
and
aij
=
0
if
j
5
ni
E
Z.
By definition the valuation
w(ai)
of
ai
is the smallest integer
j
such that
aij
#
0.
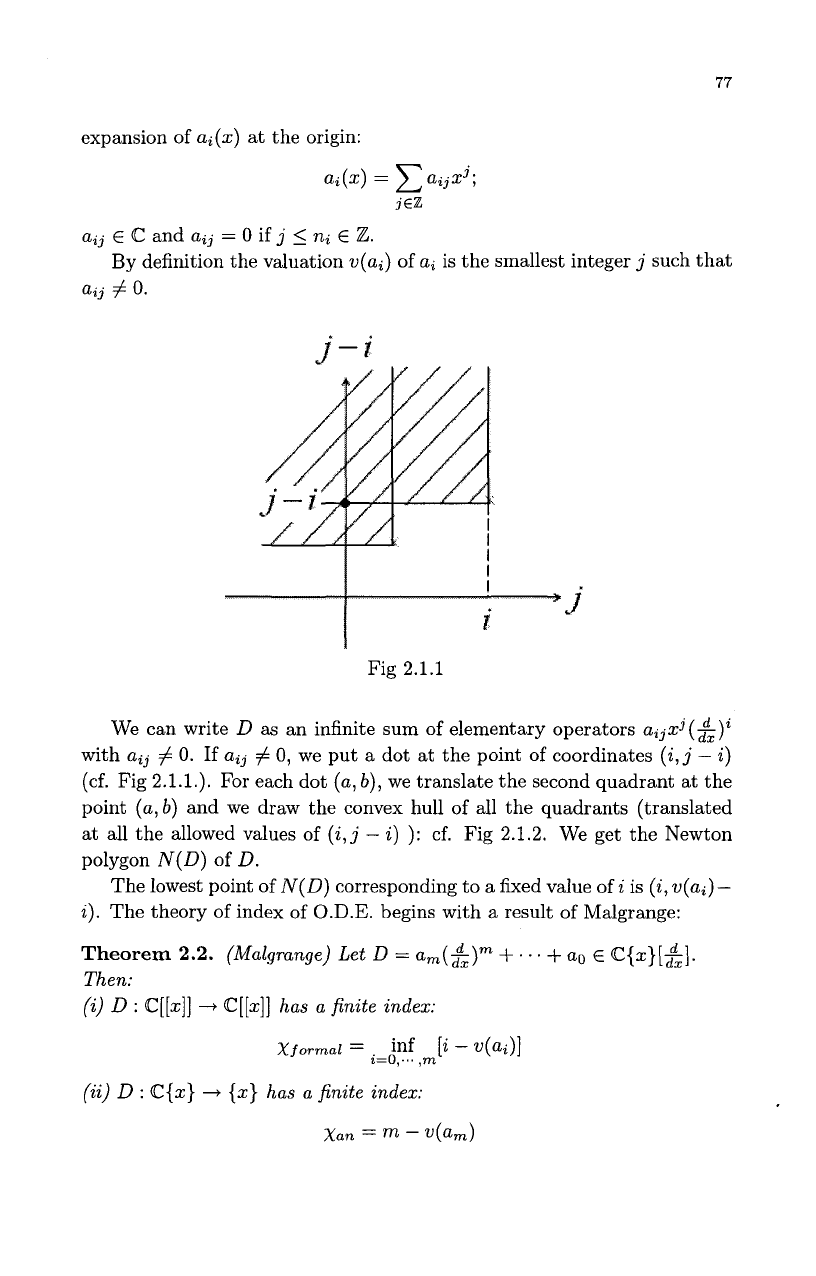
i-J
Fig 2.1.1
We can write
D
as
an infinite sum of elementary operators
aijxj(&)i
with
aij
#
0.
If
aij
#
0,
we put a dot at the point of coordinates
(i,j
-
i)
(cf. Fig 2.1.1.). For each dot
(a,
b),
we translate the second quadrant at the
point
(a,b)
and we draw the convex hull of all the quadrants (translated
at all the allowed values of
(i,j
-
i)
):
cf. Fig 2.1.2. We get the Newton
polygon
N(D)
of
D.
The lowest point of
N(D)
corresponding to a fixed value of
i
is
(i,
w(ai)-
2).
The theory of index of
O.D.E.
begins with
a
result of Malgrange:
Theorem
2.2.
(Malgrange) Let
D
=
am(&)m
t..
.
+
a0
E
C{x}[&].
Then:
(i)
D
:
C[[x]]
-+
@[[XI]
has a finite index:
(ii)
D
:
C{x}
+
{x}
has
a
finite index:
Xan
=
m
-
w(a,)

78
Fig 2.1.2
(iii)
We consider
D
:
@[[z]]/@{x}
2
@[[x]]/C{x}.
Then
D
is
surjective,
has a finite index, and
dimkerD
=
x(D)
=
Xformal-
an.
By definition
Xformal
-
xan
2
0
is the
irregularity index
of
D.
Corollary
2.1.
The following conditions are equivalent:
(i)
D
is a Fuchsian operator (regular singular);
(ii)
N(D)
is a rectangle (i.e.
it
has no strictly positive slopes);
(iii)
The irregularity index
of
D
is
zero.
Remark 2.1.
The formal index corresponds to the lowest part (horizontal
slope) of
N(D)
(with a change of sign). The analytic index corresponds to
the lowest point of the vertical slope
of
N(D)
(with
a
change of sign) which
is the dot marked for the symbol
z+n)
(&)m
of
D.
The problem of irregularity of an operator was studied by many authors:
J.
Moser, Levelt, Gkrard-Levelt, Malgrange,
N.
Katz
. .
.
In [26],
I
introduced an interpolation between Malgrange analytic and
formal indexes. The idea is to use the interpolation between
C{z}
and
C[[x]] by Gevrey spaces @[[x]IS of formal power series:
@{x}
=
@“.I10
c
@“xIls
c
@“XI1
=
@“~ll~;
@[[z]IS
increases with
s
E
(0,
+co).
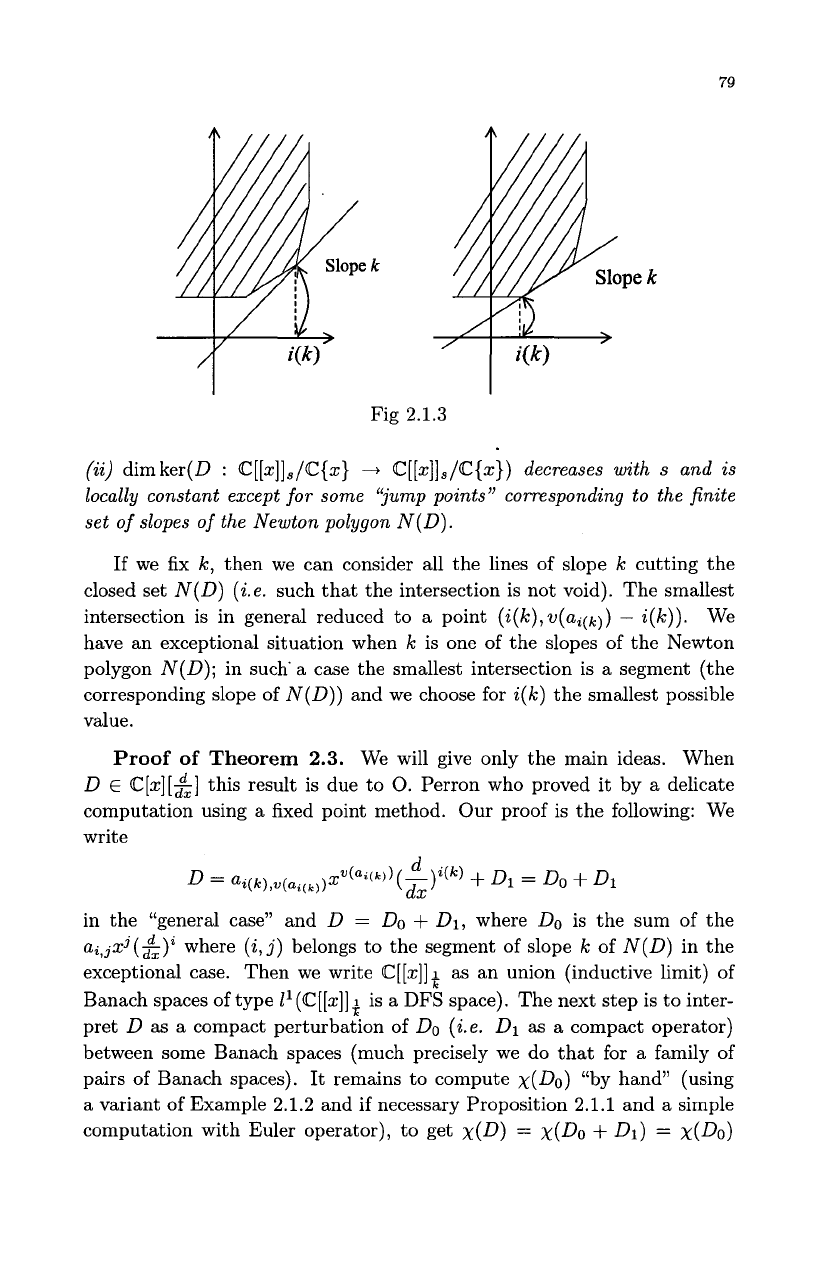
Theorem 2.3.
(Ramis) Let
s
E
[O,
+co].
We set
k
=
:.
Then:
(i)
D
:
@[[x]lS
-+
@[[x]IS
has a finite index:
xs(D)
=
i(k)
-
v(ai(k))
(cf. Fig
2.1.3)
79
Fig
2.1.3
(ii)
dimker(D
:
@[[x]IS/@{x}
-+
@[[x]]s/C{z})
decreases with
s
and
is
locally constant except
for
some ‘?jump points” corresponding to the finite
set
of
slopes
of
the Newton polygon
N(D).
If
we
fix
k,
then we can consider all the lines
of
slope
k
cutting the
closed set
N(D)
(i.e.
such that the intersection is not void). The smallest
intersection is in general reduced to a point
(i(k),v(ai(k))
-
i(k)).
We
have an exceptional situation when
k
is one of the slopes of the Newton
polygon
N(D);
in such
a
case the smallest intersection is a segment (the
corresponding slope of
N(D))
and we choose for
i(k)
the smallest possible
value.
Proof of Theorem
2.3.
We will give only the main ideas. When
D
E
@[XI[&]
this result is due to
0.
Perron who proved it by
a
delicate
computation using a fixed point method. Our proof is the following: We
write
D
=
ai(k),”(%(k,)
Z”(%.))
(-L)i(k)
+
D1
=
Do
+
D1
in the “general case” and
D
=
Do
+
D1,
where
Do
is the sum of the
ai,jxj(&)Z
where
(i,j)
belongs to the segment of slope
k
of
N(D)
in the
exceptional case. Then we write
@[[x]];
as an union (inductive limit) of
Banach spaces of type
ll(C[[x]]g
is a
DFS
space). The next step is to inter-
pret
D
as a compact perturbation of
DO
(2.e.
D1
as
a
compact operator)
between some Banach spaces (much precisely we do that for
a
family
of
pairs
of
Banach spaces).
It
remains to compute
x(D0)
“by hand” (using
a
variant
of
Example
2.1.2
and if necessary Proposition
2.1.1
and a simple
computation with Euler operator), to get
x(D)
=
DO
+
01)
=
DO)

80
using theorem 2.1.1, and to conclude by an inductive limit argument based
on Lemma 2.1.2. This proves (i).
Using Lemma 2.1.2 and (i), we get a small exact sequence
0
+
Hs
+
@“.]Is/@{.}
5
@~[.:lls/@{.}
+
0
where
Hs
=
ker(D
:
@“.]Is/@{.}
+
@“.lls/@{~})
The index
xs(D)
=
dimc ker
H,
clearly decreases with
s,
remains locally
constant except perhaps when
s
=
corresponds to
a
slope
k
of
N(D).
It
is semicontinuous on the left. We denote by
kl
>
kz
>
.
..
ke
the strictly
positive slopes (finite) of
N(D).
We set
s,.
=
2
(r
=
1,
...,
t).
Then
H,
=
Hse
if
s
2 s>;
if
s
E
[s,.,s,.+l)
then
H,
=
Hsr;
if
s
E
[O,sl),
then
H,
=
(0).
Iff
E
@[[z]]
is
a
solution of
Dy
=
g
E
@{z},
then
f^
E
@[[.I],
with
s
5
sl;
moreover, if
s
E
[s,,s,+1)
then we have exactly
f”
E
@[[x]],,.
Hence, we get the following result:
Theorem
2.4.
(Ramis)
If
D
is a linear differential operator analytic
in
a
neighborhood
of
the origin and
iff”
E
@[[XI]
is
a
formal power series solution
of
the inhomogeneous
0.
D.
E.
Dy
=
g,
where
g
E
@{x}
is convergent, then
f^
is Gevrey
of
optimal Gevrey order
s
=
1
+
i,
where
k
is one
of
the strictly
positive (finite) slopes
of
the Newton polygon
N(D)
of
D.
A
formal power series
f^
is said
of
optimal Gevrey order
s
if
f”
E
@[[XI],
and
f^
@
@[[XI],,
for any
s’
<
s.
Maillet proved (1904) that a formal power
series solution
y
=
f^
E
~[[z]]
of a (not necessarily linear) analytic
O.D.E.
G(.,
Y, Y’,.
. .
7
Y‘”9
is Gevrey of some order
s,
but his estimate for
s
is quite bad. Maillet
theorem was rediscovered in the
50s
by
K.
Mahler. Recently Malgrange
extended theorem
2.4
to the nonlinear case getting
a
new version of Maillet
theorem with optimal Gevrey estimates; he uses
a
Newton polygon along
the choosen formal solution.
2.2.
Fundamental existence theorems
Our aim is
to
“represent” a formal power series
f^
E
@[[.I]
solution of an
analytic
O.D.E.:
G(x,
y,
y’,
. .
*
,
y‘”’)
=
0

81
by an actual solution
y
=
f
(x)
of the equation, holomorphic on
a
sector and
asymptotic to
f.
As
we explained before, the story begins with
H.
Poincar6.
Many authors worked on this problem (Malmquist, Birkhoff, Hukuhara,
*
*.
),
but the complete solution is quite recent
[30].
Here we will mainly study
the linear case in relation with Gevrey estimates, Ic-summability and Stokes
phenomena.
It
is more easy to work with differential systems
(A)
Y’=A(x)Y
where
Y
is an unknown function of the complex variable
x,
taking its value
in
C”,
and
A
a given
(n,
n)
meromorphic matrix in a (small) neighborhood
of the origin.
It
is easy to derive a system from an
0.D.E
of order
n
in using the
classical trick:
Y
=
(y,
y’,
.
. .
,y@-l)).
Conversely we can derive (non uniquely) an
0.D.E
of order
n:
D,
=
0,
from
a system
(A)
using a “cyclic vector method”
[26].
The Newton polygon
N(D)
is independent
of
the choices and we can set
N(A)
=
N(D).
At the end of the century, Fabry got a fundamental system of formal
solutions for an analytic linear
0.D.E
at a singular point.
For
systems the
result is due (independently) to Hukuhara and Turrittin.
Theorem
2.5.
(Hukuhara
-
Turrittin) Let
(A)
Y’=A(x)Y
be a (germ
of)
meromorphic differential system at the origin.
admits a formal fundamental matrix solution
Then
it
F
=
fi(t)x’eQ(a)
where:
t”
=
x
(u
E
N*),
L
E
End
(rn;C)
is a constant matrix,
xL
=
e(LOgz)L,
fi
E
GL(m,C[[t]][t-’])
is a formal invertible matrix and
Q
=
(41,.
..
,qm)
is a diagonal matrix where
qi
E
$[+I
(i
=
1,
...
,
m)
(qi
can
be zero).
Example
2.3.
For the system of rank
m
=
2
associated to Airy equation
(Y
=
(y,
y’);
y”
-
ay
=
0),
we have
u=2,
t
2
=x,
2
23
2, 2
3
q2(t)
=
-t
=
-zT
q1(t)
=
--t3
=
--xT
3’
33
3
