Hooke R.L. Principles of glacier mechanics

Подождите немного. Документ загружается.

Analysis of the effect of a small change 371

Based on

flow law

(

∂q

)

∂h

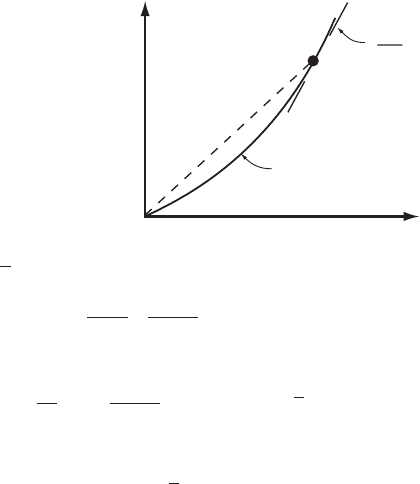
Figure 14.5. Relation

between mean speed of a

glacier and speed of a

kinematic wave.

Noting that q = uh,wehave:

q =

n + 2



ρgα



n+2

so:

c =

∂q

∂h

= 2



ρgα



n+1

= (n + 2)u (14.5)

or with n

∼

u (14.6)

In other words, the kinematic wave moves with a speed that is roughly

ﬁve times the depth-averaged velocity of the glacier. If there is basal

sliding and the sliding speed varies as τ

(Equation (7.10)), the ratio is

likely to be slightly less than 5. This relation applies, rigorously, only to

inﬁnitesimal waves. Waves of ﬁnite amplitude may have higher speeds.

Analysis of the effect of a small change in mass

balance using a perturbation approach

Let us now, following Nye (1960, pp. 561–562), use perturbation tech-

niques to study the change in thickness with time after a small change in

mass balance. Consider the situation in which the speciﬁc mass balance

is shown by the solid line in Figure 14.6.Wewill refer to the situation

represented by this solid line as the “0” or datum or equilibrium state,

and analyze the effect of small perturbations from this state such as those

represented by the dashed lines in the ﬁgure. For example, during a cold

or unusually snowy year the mass balance may be increased everywhere

by an amount b

(x, t)sowehave:

b(x, t) = b

(x ) + b

(x , t)

Note that b

is a function only of x;itdoes not vary with time because

the datum state is a steady state. Other properties of the datum state are

372 Response of glaciers to changes in mass balance

Equilibrium

line

−b

= 0

Distance from head of glacier

Cold year

Warm year

Figure 14.6. Perturbations in

mass balance from an

equilibrium state, b

(x, h, α), h

(x), and α

(x). In the perturbed state these become

q = q

+ q

, h = h

+ h

, and α = α

+ α

. Substituting these into

the continuity equation (Equation (14.2)) yields:

∂

∂x

+ q

) +

∂

∂t

+ h

) = b

+ b

(14.7)

We now write Equation (14.2)interms of the datum state, thus:

∂q

∂x

∂h

∂t

= b

and subtract this from Equation (14.7)toobtain:

∂q

∂x

∂h

∂t

= b

(14.8)

In passing, it is again worth noting that ∂h

/∂t = 0 because h

is a

property of the steady state.

At any position, x, q varies with h and α so we can write:

dq =

∂q

∂h

dh +

∂q

∂α

dα

or for small perturbations, dq = q

, dh = h

, and dα = α

so:

∂q

∂h

∂q

∂α

(14.9)

Previously we identiﬁed ∂q/∂h with the celerity of a kinematic wave,

c,orinthe datum state: (∂q/∂h)

= c

.Now we similarly deﬁne

= (∂q/∂α)

,sointhe datum state, Equation (14.9) becomes:

= c

+ D

(14.10)

This relation is valid only for small perturbations. Were we interested in

larger perturbations, terms involving h

, h

,...α

, α

,...would

have to be included. Thus, our approach is referred to as a linearized

theory.

Equations (14.8) and (14.10) are a pair of simultaneous differential

equations that can be solved for the change in ice ﬂux and thickness

Analysis of the effect of a small change 373

resulting from a perturbation in net balance. Let us ﬁrst eliminate q

from the two equations, thus:

∂c

∂x

+ c

∂h

∂x

∂ D

∂x

+ D

∂α

∂x

∂h

∂t

= b

(14.11)

Returning to Equation (14.1)wesee that in the datum and perturbed

states, respectively:

= β −

∂h

∂x

and α

+ α

= β −

∂h

∂x

−

∂h

∂x

(14.12)

Thus, subtracting the ﬁrst of these expressions from the second:

=−∂h

/∂x. This result can be substituted into Equation (14.11)

to yield, after some rearranging:

∂h

∂t

= b

−

∂c

∂x

−



−

∂ D

∂x



∂h

∂x

+ D

∂

∂x

(14.13)

(i) (ii) (iii) (iv)

Equation (14.13)was ﬁrst derived by Nye (1960,p.562). As he noted,

the terms in it have the following meanings.

(i) h

increases at a rate given by the perturbation in accumulation.

(ii) This term results in an exponential decrease or increase in the rate

of change of h

as we shall show below.

(iii) This represents a kinematic wave of constant h

. The speed of

propagation of the wave is c

− ∂D

/∂x in the +x direction. Note

that both c

and ∂D

/∂x have dimensions  t

−1

(iv) This represents diffusive damping of the perturbation h

,inaccord

with the diffusion equation, with diffusivity D

Our objective now is to solve Equation (14.13) for a simple case, neglect-

ing diffusion. Then we will investigate the role of diffusion.

Solution for a small part of a glacier with uniform

longitudinal strain rate and without diffusion

Consider a situation in which a glacier is initially in a steady state with

an accumulation rate b

(Nye, 1960,p.563). Then the accumulation rate

increases abruptly by an amount b

to b = b

+ b

and remains at this

increased level indeﬁnitely. Suppose ∂c

/∂x is independent of x on this

glacier. From Equations (14.5)wesee that:

∂c

∂x

∼

(n + 2)

∂

∂x

(14.14)

where ∂u

/∂x is the longitudinal strain rate, r

. This, thus, corresponds

to a situation in which the longitudinal strain rate is uniform in the

x-direction. We seek a solution to Equation (14.13) such that h

374 Response of glaciers to changes in mass balance

Figure 14.7. Asymptotic

adjustment of a glacier toward

a new steady state, b

/γ

following a perturbation in

accumulation rate, b

,inan

area of extending ﬂow. 1/γ

is the response time.

independent of x so ∂h

/∂x = 0. Thus, the increase in thickness is uni-

form over the glacier. We will let γ

= ∂c

/∂x.

With these simpliﬁcations, Equation (14.13) becomes:

= b

− γ

(14.15)

Separating variables we obtain:



− γ



Integration yields:



1 −e

−γ



(14.16)

If γ

is positive, corresponding to a positive longitudinal strain rate

(Equation (14.14)) such as we expect in an accumulation area, h

asymp-

totically approaches the value b

/γ

(Figure 14.7). In other words,

after a very long time, the glacier will have increased in thickness by

this amount. This is the situation described earlier and illustrated in

Figure 14.1a.

The quantity 1/γ

,which has the dimensions of time, is known as

the time constant for this change. This is sometimes associated with the

“response time” of a glacier, or the length of time required for a glacier

to respond to a change in climate. When t = 1/γ

,(1− e

−γ

)

∼

2/3

so h

is ∼2/3ofthe way to the new equilibrium state. Mathematically

(Equation (14.16)), it is clear that the new equilibrium state is never

reached. Thus, it would be meaningless to try, instead, to deﬁne the

response time as the total time required to attain a new steady state.

From Equation (14.14)wesee that 1/γ

∼

1/5r

.Inother words,

in this simple model the response time is inversely proportional to the

longitudinal strain rate. For example, typical longitudinal strain rates for

Storglaci¨aren, Barnes Ice Cap, and the Antarctic Ice Sheet are 0.015 a

−1

0.005 a

−1

, and 0.000 05 a

−1

respectively. Thus, the response time of

Effect of diffusion 375

Barnes Ice Cap might be expected to be three times as long as that of

Storglaci¨aren, and that of the Antarctic Ice Sheet, 100 times as long as

Barnes Ice Cap. While these multiples are not unrealistic, it turns out

that 1/5r

seriously underestimates the actual response time. As we will

see below, this is because diffusion has been neglected.

If γ

is negative, corresponding to longitudinal compression as

would be typical in an ablation zone, there is an obvious problem. Equa-

tion (14.16) then predicts that h

will increase exponentially with time.

Thus, a new steady state is never even approached. This is the situation

which we discussed in connection with Figure 14.1b.

Clearly, it is not possible to have the upper part of a glacier increasing

in thickness slowly and stably while the lower part is increasing rapidly

and unstably. In the absence of diffusion, Nye (1960) suggests that the

initial response in the ablation area would, indeed, be unstable. At any

location, however, stability would be restored when a kinematic wave,

initiated in the vicinity of the equilibrium line and propagating down

glacier, reached that location. With diffusion, however, such an unstable

response may never develop.

Effect of diffusion

Diffusion occurs whenever ﬂuxes are proportional to gradients. In the

present case, the ﬂux, q,isproportional to the slope (or gradient), α.

Where α is largest, on the downslope side of a wave, q is highest. Con-

versely, q is lowest on the upslope side of the wave. Thus, the ﬂux into the

wave is diminished and that out of it is enhanced. This tends to decrease

the amplitude and increase the wavelength of a wave.

As in the case of c (or c

) (Equation (14.5)), an analytical expression

for D

can be obtained by differentiating q with respect to α, thus:



∂q

∂α



= n



n + 2



ρg



n+2

n−1

or with n

∼

(14.17)

In other words, diffusion will be most signiﬁcant where the glacier is

thick, the speed high, and the slope low.

Unfortunately, it is difﬁcult to probe this dependence more thor-

oughly at the level of the treatment herein. However, Nye (1963a,

pp. 442–445) has shown that diffusion decreases the rate of thickening,

a result that is intuitively logical. As a result, the response time increases

quite markedly. In one example, the response time increases by more

than an order of magnitude (Nye, 1963a,Figure 4a). In addition, the

376 Response of glaciers to changes in mass balance

∆

(

)



Figure 14.8. Geometry of

the terminus region.

increase in thickness of the glacier near the equilibrium line is substan-

tially greater when diffusion is taken into consideration.

The problem at the terminus

It is difﬁcult to use Nye’s kinematic wave theory to study the details

of the advance and retreat of real glaciers. This is, in part, because the

mass ﬂux, q, cannot go to zero at the terminus if the glacier is to respond

to an increase in accumulation by advancing. However, Equation (14.4)

suggests that u →0ash → 0. To avoid this, Nye (1963b,p.92) assumes

that the glacier is sliding at the terminus so q = u

(

)h where u

(

)

is the sliding speed, u

,atthe terminus, 

,inthe datum state. Here



is the length of the glacier, measured from the bergschrund. Then

= ∂q/∂h = u

(

In addition, the amount of advance, ,issensitive to the assumed

geometry of the terminus. As shown in Figure 14.8:

 =

(

)

tan θ

(14.18)

where h

(

)isthe perturbation in ice thickness at the terminus. Thus

 depends on θ

Further study of the response time

J´ohannesson et al. (1989)have studied the question of response times

and of conditions at the terminus in greater detail. They identify three

possible natural time scales that might be used in the analysis of glacier

responses:



−1



(14.19a)



−1



(14.19b)



−1



(14.19c)

Further study of the response time 377

Here, t

and t

are time constants for propagation or diffusion

of a

disturbance over the length of a glacier. In effect, they are measures of

the time required to establish the general shape of the new thickness

proﬁle, h

(x, t). As the size of such a disturbance decreases with time,

the rate of propagation or diffusion also decreases. Therefore, as with

1/γ

, t

and t

are measures of the time required for the processes to

proceed about 2/3ofthe way to completion. Similarly, as we shall show

below, t

is the time required for accumulation (or loss) of about 2/3of

the volume (per unit width), V

, required to re-establish an equilibrium

geometry after a perturbation in mass balance that adds a volume of ice



to the glacier every year.

J´ohannesson et al. ﬁnd that t

is usually appreciably longer than t

or t

. This means that perturbations in ice thickness are spread out over

the glacier by propagation and diffusion rather quickly in comparison

with the time needed for accumulation of the additional mass. Clearly, a

glacier cannot be considered to have returned some speciﬁed fraction of

the way to a new equilibrium state until the necessary additional mass

has accumulated (or been lost).

In an extension of the Nye theory, t

would be viewed approximately

as follows: at any given time after a perturbation in mass balance, the

mean perturbation in thickness, averaged over the length of the glacier,

would equal the perturbation at the terminus, h

(

,t), multiplied by some

function of the conditions in the datum state, of the magnitude of the

perturbation, b

, and of time, thus:

(x , t) = f (c

, D

, b

, t) · h

(

, t) (14.20)

Remember that 

is the position of the terminus in the datum state. Once

anew equilibrium geometry has been attained, at t =∞, the increase in

volume of the glacier would be obtained by multiplying Equation (14.20)

by the length of the glacier, thus:

= h



= f (t =∞) ·h

(

, ∞)

(14.21)

However, once a new steady state has been attained, the annual mass

gain resulting from the perturbation,



, must equal the ﬂux past the

old terminus position, u

(

)·h

, thus:



= u

(

, ∞) (14.22)

Eliminating h

from these two equations yields:

f (t =∞)



(

)

(14.23)

The π

term in Equation (14.19b) comes from the Fourier solution of the diffusion

equation (T. J´ohannesson, written communications dated November 7 and 14, 1996).

378 Response of glaciers to changes in mass balance

∆



∆

0 max

Figure 14.9. Geometrical argument for evaluating t

. During an advance, ,

the mass that must be added to a glacier is approximately ·h

0max

Whence, from Equation (14.19c):

f (t =∞)

(

)

(14.24)

Thus, by this approach, t

turns out to be sensitive to the unknown sliding

speed at the terminus. In addition, the function, f,ishighly sensitive to

the details of the variations in c

and D

, especially near the terminus

(J´ohannesson et al., 1989,p.364 and appendices).

J´ohannesson et al.havedeveloped a much simpler geometrical argu-

ment to estimate t

. Consider the situation in Figure 14.9 in which an

advance of a glacier by an amount  is illustrated graphically by cutting

the glacier at its point of maximum thickness and sliding the lower part

forward by . Then, the increase in volume of the glacier is approx-

imately ·h

0max

. Detailed numerical modeling suggests that this is a

good approximation to the response of a real glacier when the dynamical

properties of the glacier are the same in the initial and ﬁnal state, and

thus inﬂuence the initial and ﬁnal proﬁles in the same way. Now, rather

than equate the annual mass gain resulting from the perturbation with

the ﬂux past the old terminus position, as in Equation (14.22), we equate

it with the mass loss over the new part of the glacier, , thus:



 (14.25)

where b

is the mean net balance rate over  which may be approximated

by b(

), the net balance rate at the terminus (a negative quantity) if 

is small. Therefore:

= h

0 max



b(

)

(14.26)

Whence, from Equation (14.19c):

0 max

b(

)

(14.27)

Further study of the response time 379

Thus, t

can be estimated, quite easily, from knowledge of the thickness

of the glacier and the net balance rate at the terminus.

We noted above that t

is a time constant in the same sense that 1/γ

is. Let us now demonstrate this. Immediately after a permanent change

in balance rate, b

, the rate at which additional mass, V

,isacquired

by the glacier, dV

/dt,isB

= b



.However, as the glacier becomes

longer (by an amount (t)), some of the additional annual input is lost

through ablation in the new part of the terminus region. Thus:

= B

−

(

)



Now from Equation (14.26)orFigure 14.9, 

∼

0max

, so:

= B

−

(

)

0 max

Comparing this with Equation (14.15), it is clear that h

0 max

b(

)

the analog of 1/γ

When calculating t

in practice, the three-dimensional geometry

of the glacier must be taken into consideration. Thus, in the case

of a glacier like Storglaci¨aren that has a number of overdeepened

basins in its longitudinal proﬁle, h

0max

needs to be replaced by an

appropriate longitudinally averaged thickness. In addition, the termi-

nus of Storglaci¨aren is constrained between bedrock and morainal highs

so that its width is about half the average width of the glacier (Figure

12.9). Accordingly, Equations (14.25)to(14.27) need to be generalized

to three dimensions. For example, if we write Equation (14.25) as:

b(

)

W (

) (14.28)

where A

is the initial area of the glacier and W(

)isthe width of the

terminus, Equation (14.19c) becomes:

(14.29)

must now be estimated based on the glacier geometry. For instance,

by analogy with Figure 14.9, one might consider that the new geometry

could be approximated by (mentally) sliding forward the central part of

the glacier of width W(

). V

is then h

0max

W(

) ,where h

max

is a

mean thickness over this central part. Inserting this in Equation (14.29)

and using Equation (14.28) then yields:

0 max

b(

)

(14.30)

Harrison et al.(2001)have pointed out that the formulation of t

in Equation (14.19c) ignores the normal increase in b

with elevation.

Owing to this increase, perturbations that result in thickening or thinning

380 Response of glaciers to changes in mass balance

of a glacier are effectively ampliﬁed. This positive feedback, known

as the B¨o

varsson effect (B¨oðvarsson, 1955), can lead to signiﬁcant

underestimates of the response time. In extreme cases, it may lead to

unstable (or runaway) growth or shrinkage of a glacier.

To include this effect, Harrison et al. suggest adding a term to Equa-

tion (14.27), thus:

− G

(14.31)

H is now a thickness scale, not necessarily equal to h

0 max

, b

is an effective

balance rate at or just below the terminus, and G

is the effective budget

gradient. The subscript H is added to t

to distinguish this time scale from

that of J´ohannesson et al. (Readers should refer to Elsberg et al.(2001)

and Harrison et al.(2001) for a rigorous derivation of Equation (14.31)

and deﬁnitions of b

, G

, and H. Sufﬁce it to say here that the theory is

grounded in the reference-surface approach to mass balance discussed

brieﬂy in Chapter 3 (p. 25).) It will be readily seen that the added term

has the desired effect. Both G

and H are positive, so subtracting G

from |b

| in the denominator increases t

and in extreme cases may

make t

negative – the unstable response.

Unfortunately, b

, G

, and H are not easy to determine. To evaluate

one needs detailed balance rate data from the terminus that can be

extrapolated into the area below the terminus and also a map showing

bed elevations in the terminus area. In an application of their theory to

South Cascade Glacier in the state of Washington (USA), Elsberg et al.

(2001) found that setting b

≈ 0.75 b(

) yielded a good approximation

to the true value. Likewise, rigorously H = dV/dA and neither V nor

A are measured routinely. Finally, an average value of G

may not be

appropriate; again Elsberg et al.(2001) found that setting G

equal to 0.9

times the speciﬁc balance gradient half way between the terminus and the

equilibrium line worked well on South Cascade Glacier, but they caution

that these approximations may not be appropriate for other glaciers.

An important characteristic of Equation (14.31) appears if one notes

that since b

is a balance rate near the terminus, and b

= 0atthe

equilibrium line, then b

/z

t→e

≈ G

,where z

t→e

is the elevation

difference between the terminus and the equilibrium line. Then the ratio

of the two terms in the denominator of Equation (14.31) is:

≈

z

t→e

Clearly, t

becomes large as this ratio approaches unity, and the system

is unstable if it exceeds unity. z

t→e

will be smaller on glaciers that are

relatively ﬂat, and may approach H on such glaciers. Thus glaciers with