Honkela A. Solutions to Selected Problems on Independent Component Analysis
Подождите немного. Документ загружается.


Antti Honkela ICA: Exercise solutions
0 0.2 0.4 0.6 0.8 1 1.2
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
y (* x)
p(y|x) (* 1/x)
Figure 1: A plot of the posterior distribution p
y|x
(y|x) from Problem 4.17.1.
Problems for Chapter 5
Problem 5.3
h(x) = E{−log p
x
(x)} = E
(
ln(
√
2σ) +
√
2
σ
|x|
)
= ln(
√
2σ) +
√
2
σ
E{|x|} (56)
The remaining expectation can be evaluated as
√
2
σ
E{|x|} =
√
2
σ
Z
∞
−∞
|x|p
x
(x)dx =
2
√
2
σ
Z
∞
0
x
1
√
2σ
exp
Ã
−
√
2
σ
x
!
dx
=
Z
∞
0
√
2
σ
x exp
Ã
−
√
2
σ
x
!
√
2
σ
dx =
Z
∞
0
t exp(−t)dt = 1.
(57)
Thus the differential entropy is
h(x) = ln(
√
2σ) + 1 = ln(
√
2eσ). (58)
Problem 5.5
Let x ∼ N (0, Σ), i.e.
p(x) = (2π)
−n/2
|det Σ|
−1/2
e
1
2
x
T
Σ
−1
x
.
The differential entropy is defined as
h(x) = −E{log(p(x))} =
1
2
E{n log(2π) + log(|det Σ|) + x
T
Σ
−1
x}.
HUT, Neural Networks Research Centre 10
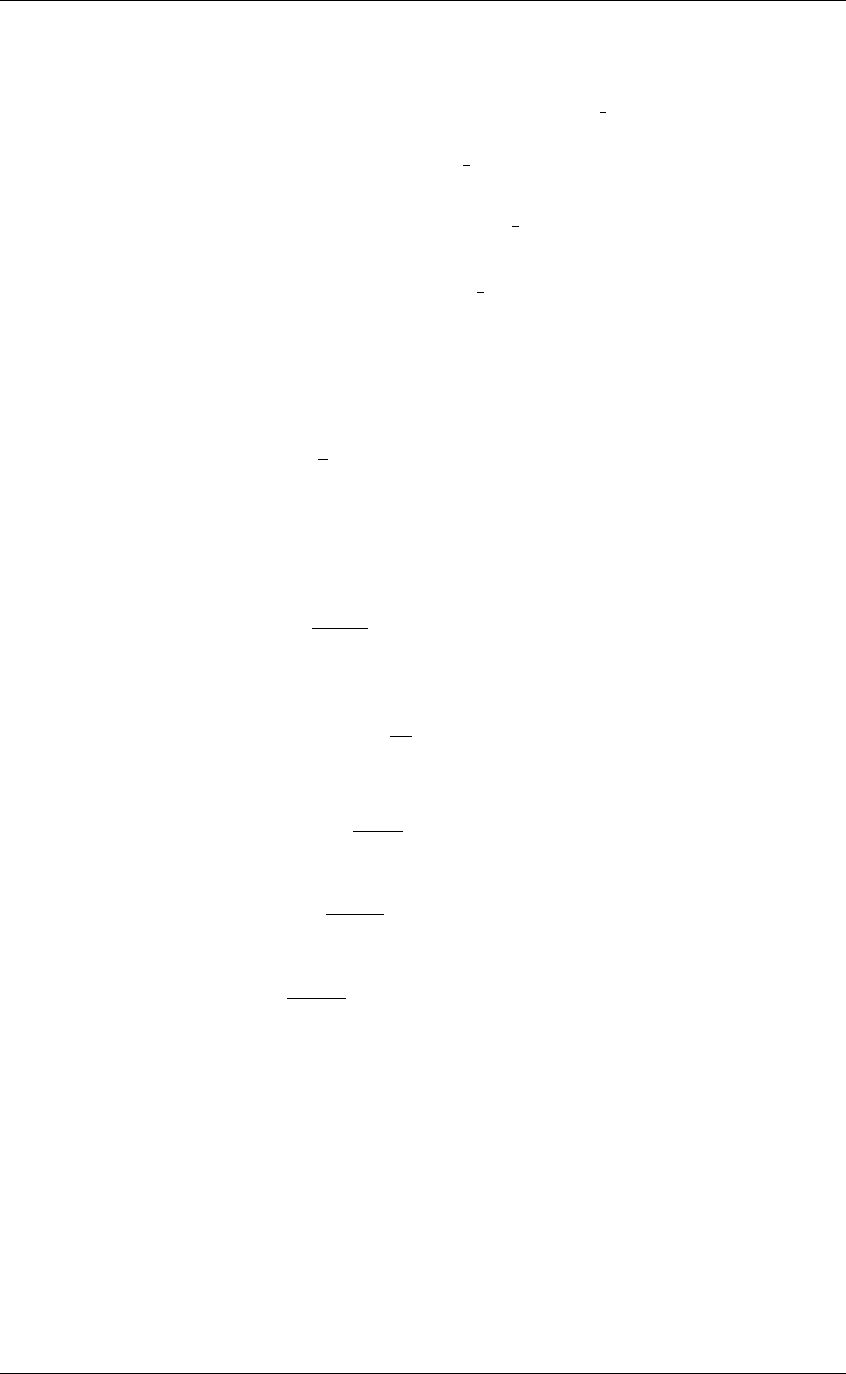
Antti Honkela ICA: Exercise solutions
Two first terms are constants and the last can be computed as
E{x
T
Σ
−1
x} =
Z
R
n
x
T
Σ
−1
x(2π)
−n/2
|det Σ|
−1/2
e
−
1
2
x
T
Σ
−1
x
dx
=
Z
R
n
y
T
y(2π)
−n/2
e
−
1
2
y
T
y
dy
=
Z
R
n
Ã
n
X
i=1
y
2
i
!
(2π)
−n/2
e
−
1
2
y
T
y
dy
=
n
X
i=1
Z
R
n
y
2
i
(2π)
−n/2
e
−
1
2
y
T
y
dy
=
n
X
i=1
Var[N(0, 1)] =
n
X
i=1
1 = n,
which gives
h(x) =
1
2
[n + n log(2π) + log(|det Σ|)] . (59)
Problem 5.7
The Chebysev-Hermite polynomials H
i
are defined by
∂
i
ϕ(ξ)
∂ξ
i
= (−1)
i
H
i
(ξ)ϕ(ξ), (60)
where i = 0, 1, . . . and ϕ(ξ) is the pdf of N (0, 1),
ϕ(ξ) =
1
2π
exp(−ξ
2
/2). (61)
Obviously H
0
(x) = 1 ∀x.
∂ϕ(ξ)
∂ξ
= −ξϕ(ξ) (62)
and thus H
1
(x) = x.
∂
2
ϕ(ξ)
∂ξ
2
= −ϕ + ξ
2
ϕ(ξ) (63)
yielding H
2
(x) = x
2
− 1.
∂
3
ϕ(ξ)
∂ξ
3
= ξϕ + 2ξϕ(ξ) − ξ
3
ϕ(ξ) (64)
and so H
3
(x) = x
3
− 3x.
Problems for Chapter 6
Problem 6.1
Var{y
m
} = E{y
2
m
} = E{w
T
m
xx
T
w
T
m
} = w
T
m
E{xx
T
}w
T
m
= w
T
m
C
x
w
m
(65)
The constraints:
w
T
k
w
l
=
(
1 if k = l
0 if k 6= l
(66)
HUT, Neural Networks Research Centre 11

Antti Honkela ICA: Exercise solutions
The Lagrangian function:
L(w
m
, λ) =
1
2
w
T
m
C
x
w
m
+ λ
0
(w
T
m
w
m
− 1) +
m−1
X
i=1
λ
i
w
T
m
w
i
(67)
and its derivative
L
w
m
= C
x
w
m
+ λ
0
w
m
+
m−1
X
i=1
λ
i
w
i
. (68)
Letting m = 1 and setting the derivative to zero yields
C
x
w
1
= −λ
0
w
1
(69)
which implies that w
1
is an eigenvector of C
x
.
Evaluating the variance of y:
Var{y
1
} = Var{w
T
1
x} = E{w
T
1
xx
T
w
1
} = w
T
1
C
x
w
1
= w
T
1
(−λ
0
w
1
) = −λ
0
. (70)
This is maximized when −λ
0
is equal to the largest eigenvalue of C
x
and w
1
is the corresponding
eigenvector.
Let us now continue inductively. For m > 1, the previous weight vectors w
i
, i = 1, . . . , m − 1 are
the eigenvectors corresponding to m −1 largest eigenvalues. By multiplying Eq. (68) from the left
by w
i
, i = 1, . . . , m − 1, we get λ
i
= 0 for all i. Thus again
C
x
w
m
= −λ
0
w
m
. (71)
Thus w
m
is again an eigenvector and to maximize the variance it must be the one with the largest
remaining eigenvalue.
NB: Remember that C
x
is a symmetric matrix and thus its eigenvalues are real and eigenvectors
orthogonal.
Problem 6.4
Maximize y = (w
T
x)
2
= w
T
xx
T
w under constraint ||w|| = 1.
6.4.1
∂y
∂w
= 2xx
T
w = 2(w
T
x)x. (72)
Thus the gradient ascent updates are
w ← w + γ(w
T
x)x. (73)
Evaluating the norm of the new iterate
||w + γ(w
T
x)x||
2
=
¡
w + γ(w
T
x)x
¢
T
¡
w + γ(w
T
x)x
¢
= w
T
w + 2γw
T
(w
T
x)x + γ
2
(w
T
x)
2
x
T
x
= ||w||
2
+ 2γ(w
T
x)
2
+ γ
2
(w
T
x)
2
||x||
2
≥ ||w||
2
(74)
HUT, Neural Networks Research Centre 12

Antti Honkela ICA: Exercise solutions
6.4.2
f(γ) =
w + γ(w
T
x)x
||w + γ(w
T
x)x||
=
w + γ(w
T
x)x
p
||w||
2
+ 2γ(w
T
x)
2
+ γ
2
(w
T
x)
2
||x||
2
=
w + γ(w
T
x)x
p
1 + 2γ(w
T
x)
2
+ γ
2
(w
T
x)
2
||x||
2
=
g(γ)
h(γ)
(75)
g
0
(γ) = (w
T
x)x (76)
h
0
(γ) = h(γ)
−1
¡
(w
T
x)
2
+ γ(w
T
x)
2
||x||
2
¢
(77)
h
0
(0) = (w
T
x)
2
(78)
f(0) = w (79)
f
0
(0) =
h(0)g
0
(0) − h
0
(0)g(0)
h(0)
2
=
1(w
T
x)x − (w
T
x)
2
w
1
(80)
Thus the Taylor expansion yields
w ← w + γ[(w
T
x)x − (w
T
x)
2
w] + O(γ
2
) (81)
6.4.3
At a stationary point
E{(w
T
x)x − (w
T
x)
2
w} = E{(xx
T
)w − (w
T
xx
T
w)w} = C
x
w − (w
T
C
x
w)w = 0 (82)
which implies
C
x
w = (w
T
C
x
w)w. (83)
6.4.4
The value w
T
C
x
w is a scalar and thus Eq. (83) has the form of the eigenvalue equation of matrix
C
x
.
Problems for Chapter 7
Problem 7.1
The claim in the problem statement in its original form is not true as D
−1/2
is not uniquely defined.
A diagonal matrix with square roots of the diagonal elements on the diagonal is always a solution,
and the signs of the individual elements can be chosen arbitrarily. If some of the eigenvalues of
the covariance matrix are equal, there are even more (actually infinitely many) solutions.
The errata of the book suggests a modification to the problem so that only symmetric positive
semidefinite whitening matrices are studied. In this case the solution is indeed unique. This
follows rather directly from the fact that the symmetric positive semidefinite square root of a
symmetric positive semidefinite matrix is unique. The proof of this fact is somewhat difficult and
thus omitted here.
Let the whitening matrix be of the form V = EME
T
. Clearly any whitening matrix can be
written in this form for some M. V is symmetric if and only if M is symmetric. Similarly V is
positive semidefinite if and only if M is positive semidefinite.
HUT, Neural Networks Research Centre 13

Antti Honkela ICA: Exercise solutions
As V is a whitening matrix, it must satisfy
E{zz
T
} = VC
x
V
T
= VEDE
T
V
T
= EM(E
T
E)D(E
T
E)ME
T
= EMDME
T
= I.
(84)
Multiplying this from the left by E
T
and from the right by E yields
MDM = I. (85)
Taking the inverse of both sides and multiplying the result from both sides by M yields
D
−1
= M
2
. (86)
Thus M must be the unique symmetric positive semidefinite square root D
−1/2
of D
−1
.
Problem 7.4
Assuming x = As with A invertible, the model does not change if the data is multiplied by an
invertible matrix M:
z = Mx = (MA)s =
˜
As (87)
and while the mixing matrix changes, the independent components stay the same. If M is not
invertible, then the model does not hold anymore.
Problem 7.6
If there are more independent components than observed mixtures, we in general cannot recover
the values of the independent components. Finding the values of the components would involve
solving a set of linear equations where there are more unknowns than equations and such sets have
an infinite number of solutions.
If there are more observed mixtures than independent components, the situation reverses: now we
have more equations than unknowns. If the data really is generated by mixing the independent
components, there must be a solution to the equations and thus we can recover the components.
Problems for Chapter 8
Problem 8.2
kurt(y) = E{y
4
} − 3(E{y
2
})
2
(88)
kurt(w
T
z) = E{(w
T
z)
4
} − 3(E{(w
T
z)
2
})
2
(89)
|kurt(w
T
z)| = sign
¡
kurt(w
T
z)
¢
E{(w
T
z)
4
} − 3(E{(w
T
z)
2
})
2
(90)
∂|kurt(w
T
z)|
∂w
= sign
¡
kurt(w
T
z)
¢
∂(E{(w
T
z)
4
} − 3(E{(w
T
z)
2
})
2
)
∂w
= sign
¡
kurt(w
T
z)
¢
E{4(w
T
z)
3
z} − 3 · 2 E{(w
T
z)
2
}E{2(w
T
z)z}
= 4sign
¡
kurt(w
T
z)
¢
(E{z(w
T
z)
3
} − 3||w||
2
E{(zz
T
)}w)
= 4sign
¡
kurt(w
T
z)
¢
(E{z(w
T
z)
3
} − 3||w||
2
w)
(91)
HUT, Neural Networks Research Centre 14

Antti Honkela ICA: Exercise solutions
Problem 8.4
Assuming g(x) = x, the algorithm in Eq. (8.28):
∆w = γ E{zg(w
T
z)} = γ E{zz
T
}w. (92)
If z is white, the direction of w will never change. If z is not yet white, the method is essentially
the power method of solving the eigenvector related to the largest eigenvalue of the covariance of
z, i.e. PCA.
Applying the same for Eq. (8.43) yields:
w = E{zg(w
T
z) − E{g
0
(w
T
z)}w} = E{(zz
T
)w − E{I}w} = (E{(zz
T
)} − I)w (93)
which is essentially the same as the previous.
Problem 8.6
The third cumulant
E{y
3
} = E{(w
T
z)
3
} (94)
∂ E{(w
T
z)
3
}
∂w
= E{3(w
T
z)
2
z} (95)
Following the reasoning of Section 8.2.3, we get a fixed point algorithm
w ← E{(w
T
z)
2
z} (96)
w ← w/||w|| (97)
This algorithm could be useful when extracting independent components that have highly asym-
metrical distributions. The kurtosis is usually preferred because the third cumulant is identically
zero for all symmetrical distributions and the derived algorithm cannot separate such distributions.
Problem 8.7
8.7.1
The constraint is
1 = q
2
1
+ q
1
2
= t
1
+ t
2
. (98)
Geometrically this is a line segment from (0, 1) to (1, 0).
8.7.2
The contours of F (t) are ellipses, as shown in Fig. 2.
8.7.3
Because of the absolute values in F this reduces to 8.7.2.
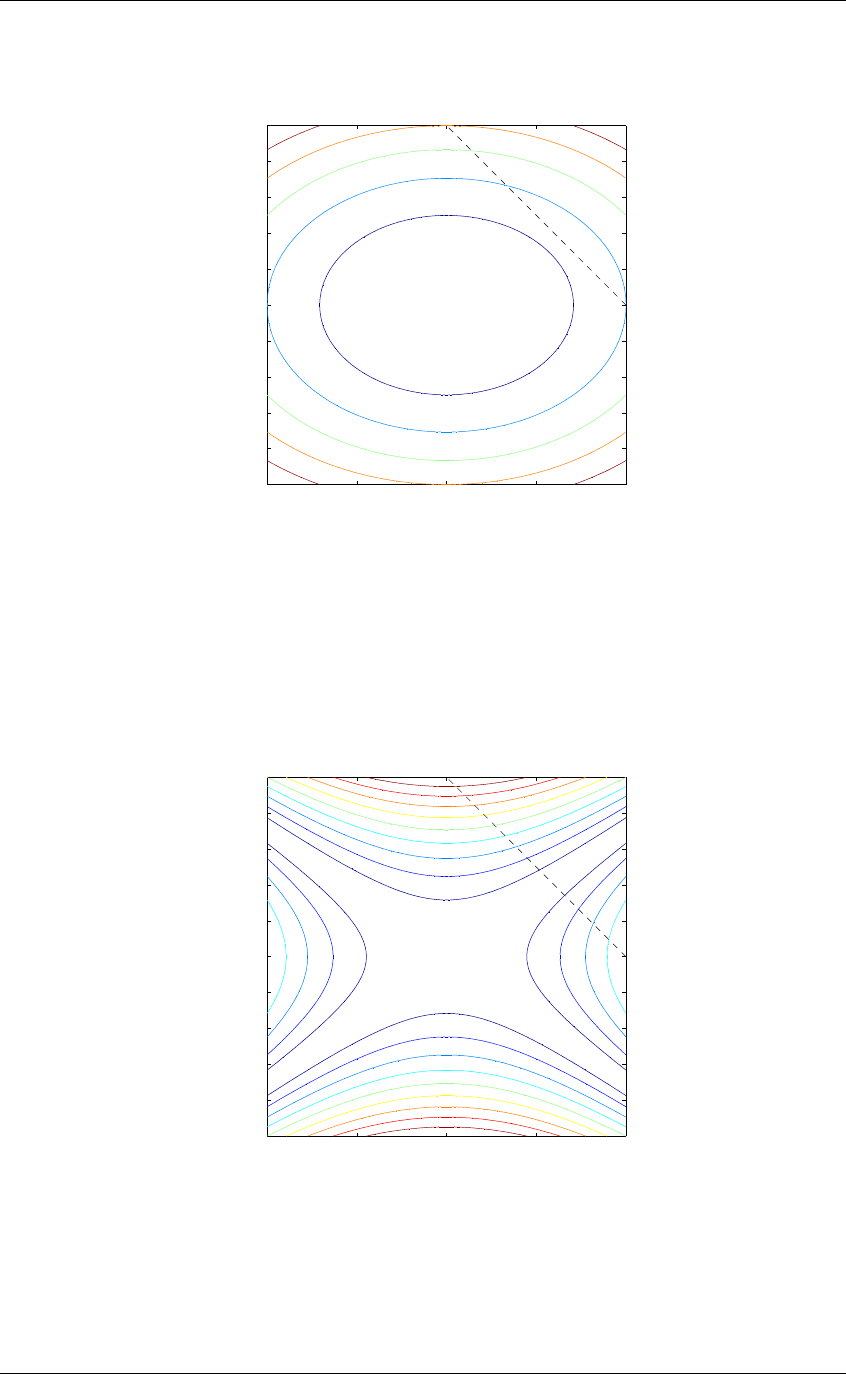
8.7.4
The contours of F (t) are now hyperbolas, as shown in Fig. 3.
HUT, Neural Networks Research Centre 15
Antti Honkela ICA: Exercise solutions
−1 −0.5 0 0.5 1
−1
−0.8
−0.6
−0.4
−0.2
0
0.2
0.4
0.6
0.8
1
t
1
t
2
Figure 2: A plot of the contours of the objective function of Problem 8.7 in the case kurt(s
1
) =
±1, kurt(s
2
) = ±2. The dashed black line shows the line segment satisfying the constraints of the
problem.
−1 −0.5 0 0.5 1
−1
−0.8
−0.6
−0.4
−0.2
0
0.2
0.4
0.6
0.8
1
t
1
t
2
Figure 3: A plot of the contours of the objective function of Problem 8.7 in the case kurt(s
1
) =
∓1, kurt(s
2
) = ±2. The dashed black line shows the line segment satisfying the constraints of the
problem.
HUT, Neural Networks Research Centre 16
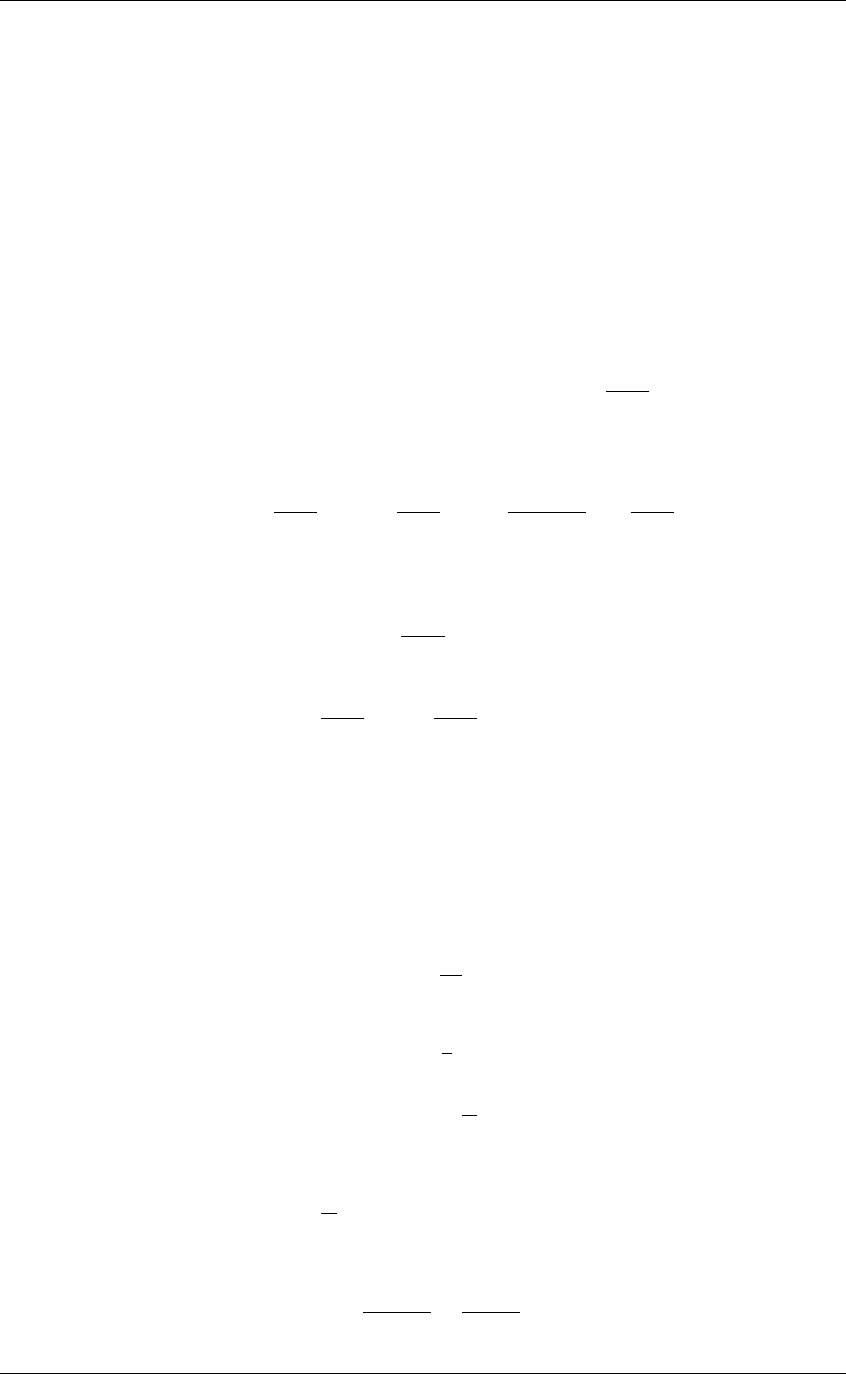
Antti Honkela ICA: Exercise solutions
8.7.5
By Eq. (98)
t
2
= 1 − t
1
. (99)
Letting a = kurt(s
1
) and b = kurt(s
2
), we are to maximize
F (t
1
) = |at
2
1
+ b(1 − t
1
)
2
| = |(a + b)t
2
1
− 2bt
1
+ b| (100)
on the interval t
1
∈ [0, 1].
The maximum may be either at the end points of the interval or at a zero or discontinuity of
the derivative F
0
(t
1
). The derivative is discontinuous when the formula inside the absolute value
changes its sign, but those points correspond to minima.
F
0
(t
1
) = sign(F (t
1
))2(a + b)t
1
− 2b = 0 ⇒ t
∗
1
=
b
a + b
. (101)
The value of the function at this point is
F (t
∗
1
) =
¯
¯
¯
¯
¯
a
µ
b
a + b
¶
2
+ b
µ
a
a + b
¶
2
¯
¯
¯
¯
¯
=
¯
¯
¯
¯
ab(a + b)
(a + b)
2
¯
¯
¯
¯
=
¯
¯
¯
¯
ab
a + b
¯
¯
¯
¯
(102)
For the minimum to belong to the interval [0, 1] it must satisfy
0 ≤
b
a + b
≤ 1 (103)
Thus
¯
¯
¯
¯
ab
a + b
¯
¯
¯
¯
= |a|
¯
¯
¯
¯
b
a + b
¯
¯
¯
¯
≤ |a| (104)
and the maximum is max(|a|, |b|), attained at the appropriate end of the interval.
Problems for Chapter 9
Problem 9.4
Setting
g(y) = −y
3
=
∂
∂y
log p(y) (105)
yields
log p(y) = −
1
4
y
4
+ C (106)
and thus
p(y) = Ce
−
y
4
4
. (107)
The normalizing constant can be solved by integrating
1 =
Z
∞
−∞
p(y) dy = 2C
Z
∞
0
e
−
y
4
4
dy = 2C
Z
∞
0
(4t)
−3/4
e
−t
dt = 2C4
−3/4
Γ(1/4). (108)
Solving for C yields
C =
4
3/4
2Γ(1/4)
=
4
1/4
Γ(1/4)
, (109)
HUT, Neural Networks Research Centre 17

Antti Honkela ICA: Exercise solutions
where Γ(x) =
R
∞
0
t
x−1
e
−
t dt is the gamma function.
To evaluate the kurtosis, we need also the second and fourth moments of the distribution. The
fourth moment is easy and can be evaluated without the gamma function:
E{y
4
} =
Z
∞
−∞
y
4
p(y) dy = −2C
Z
∞
0
y
µ
−y
3
e
−
y
4
4
¶
dy
= −2C
Ã
·
ye
−
y
4
4
¸
∞
y=0
−
Z
∞
0
e
−
y
4
4
dy
!
= 0 + 2C
Z
∞
0
e
−
y
4
4
dy = 1.
(110)
The second moment is a bit more tricky:
E{y
2
} =
Z
∞
−∞
y
2
p(y) dy = 2C
Z
∞
0
y
2
e
−
y
4
4
dy = 2C
Z
∞
0
(4t)
−1/4
e
−t
dy
= 2C4
−1/4
Γ(3/4) = 2
Γ(3/4)
Γ(1/4)
≈ 0.6760
(111)
Combining these yields the kurtosis
kurt(y) = E{y
4
} − 3(E{y
2
})
2
= 1 − 3
µ
2
Γ(3/4)
Γ(1/4)
¶
2
≈ −0.3708. (112)
As the kurtosis is negative, the distribution is subgaussian. The numerical calculations involving
the gamma function can be done with practically any numerical software, like Matlab.
Problem 9.6
Setting
g(y) = −y =
∂
∂y
log p(y) (113)
yields
log p(y) = −
1
2
y
2
+ C (114)
and thus
p(y) = Ce
−
y
2
2
, (115)
a Gaussian. As Gaussian distributions are not allowed in the ICA model, this is not a valid choice
for g(y).
Problem 9.8
E{sg(s) − g
0
(s)} =
Z
∞
−∞
(sg(s) − g
0
(s))p(s)ds =
1
√
2π
Z
∞
−∞
(sg(s) − g
0
(s))e
−
s
2
2
ds
=
1
√
2π
µ
Z
∞
−∞
g(s)
³
se
−
s
2
2
´
ds −
Z
∞
−∞
g
0
(s)e
−
s
2
2
ds
¶
=
1
√
2π
µ
h
−g(s)e
−
s
2
2
i
∞
s=−∞
+
Z
∞
−∞
g
0
(s)e
−
s
2
2
ds −
Z
∞
−∞
g
0
(s)e
−
s
2
2
ds
¶
= 0
(116)
Assuming that g(s) grows slower than e
s
2
. (Otherwise the first integral would not converge.)
HUT, Neural Networks Research Centre 18

Antti Honkela ICA: Exercise solutions
Problems for Chapter 11
Problem 11.1
W diagonalizes F(M) if WF(M)W
T
is diagonal. By Eq. (11.9)
M =
k
X
j=1
α
j
w
j
w
T
j
. (117)
By the linearity of the cumulant tensor (Eq. (11.2)) and Eq. (11.8)
F
ij
(M) = F
ij
(
k
X
l=1
α
l
w
l
w
T
l
) =
k
X
l=1
α
l
F
ij
(w
l
w
T
l
) =
k
X
l=1
α
l
w
li
w
lj
kurt(s
l
). (118)
This implies that
F(M) = W
T
diag(α
l
kurt(s
l
))W (119)
and now a direct calculation shows that
WF(M)W
T
= (WW
T
) diag(α
l
kurt(s
l
))(WW
T
) = diag(α
l
kurt(s
l
)) (120)
which is obviously diagonal.
Problem 11.2
E{ss
T
||s||
2
}
ij
= E{s
i
s
j
X
k
s
2
k
} =
X
k
E{s
i
s
j
s
2
k
} =
X
k
δ
ij
E{s
2
i
s
2
k
}
= δ
ij
(E{s
4
i
} +
X
k6=i
E{s
2
i
s
2
k
})
= δ
ij
(E{s
4
i
} + E{s
2
i
}
X
k6=i
E{s
2
k
}) = δ
ij
(E{s
4
i
} + n − 1)
(121)
and on the other hand
E{ss
T
||s||
2
}
ij
=
X
k
δ
ij
E{s
2
i
s
2
k
} = δ
ij
E{s
2
i
X
k
s
2
k
} = δ
ij
E{s
2
i
||s||}. (122)
Combined, these imply (11.19):
Ω = W
T
E{ss
T
||s||
2
}W = W
T
diag(E{s
2
i
||s||})W = W
T
diag(E{s
4
i
} + n − 1)W (123)
Problems for Chapter 12
Problem 12.1
In this case the implicit update equations are
∆m
12
= µy
3
1
y
2
(124)
∆m
21
= µy
3
2
y
1
. (125)
The values of y
1
and y
2
can be solved directly from Eqs. (12.6) and (12.7). Substituting (12.6) in
(12.7) yields
y
2
= x
2
− m
21
(x
1
− m
12
y
2
) (126)
HUT, Neural Networks Research Centre 19
