Holton, James R. An Introduction to Dynamic Meteorology
Подождите немного. Документ загружается.


January 27, 2004 17:12 Elsevier/AID aid
APPENDIX C
Vector Analysis
C.1 VECTOR IDENTITIES
The following formulas may be shown to hold where is an arbitrary scalar
and A and B are arbitrary vectors.
∇ × ∇ = 0
∇·
(
A
)
= ∇·
(
A
)
+ A ·∇
∇ ×
(
A
)
= ∇ × A +
(
∇ × A
)
∇·
(
∇ × A
)
= 0
(
A ·∇
)
A =
1
2
∇
(
A · A
)
− A ×
(
∇ × A
)
∇ ×
(
A × B
)
= A
(
∇·B
)
− B
(
∇·A
)
−
(
A·∇
)
B +
(
B·∇
)
A
A ×
(
B × C
)
=
(
A · C
)
B −
(
A · B
)
C
498
January 27, 2004 17:12 Elsevier/AID aid
C vector analysis 499
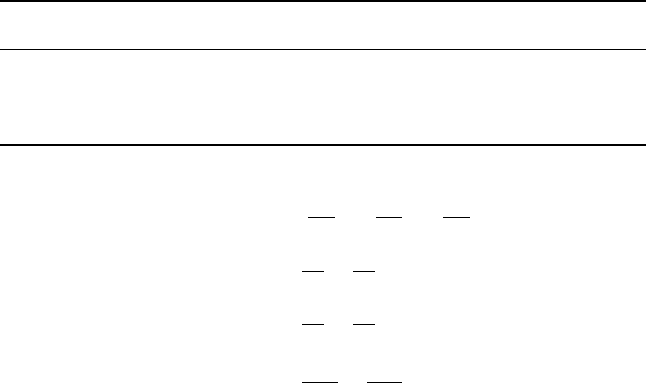
C.2 INTEGRAL THEOREMS
(a) Divergence theorem:
A
B · ndA =
V
V · BdV
where V is a volume enclosed by surface A and n is a unit normal on A.
(b) Stokes’ theorem:
B · dl =
A
(
V × B
)
· ndA
where A is a surface bounded by the line traced by the position vector l and n is a
unit normal of A.
C.3 VECTOR OPERATIONS IN VARIOUS COORDINATE SYSTEMS
(a) Cartesian coordinates: (x,y,z)
Coordinate Symbol Velocity component Unit vector
Eastward xu i
Northward yv j
Upward zw k
∇ = i
∂
∂x
+ j
∂
∂y
+ k
∂
∂z
∇·V =
∂u
∂x
+
∂v
∂y
k ·
(
∇ × V
)
=
∂v
∂x
−
∂u
∂y
∇
2
h
=
∂
2
∂x
2
+
∂
2
∂y
2
January 27, 2004 17:12 Elsevier/AID aid
500 C vector analysis
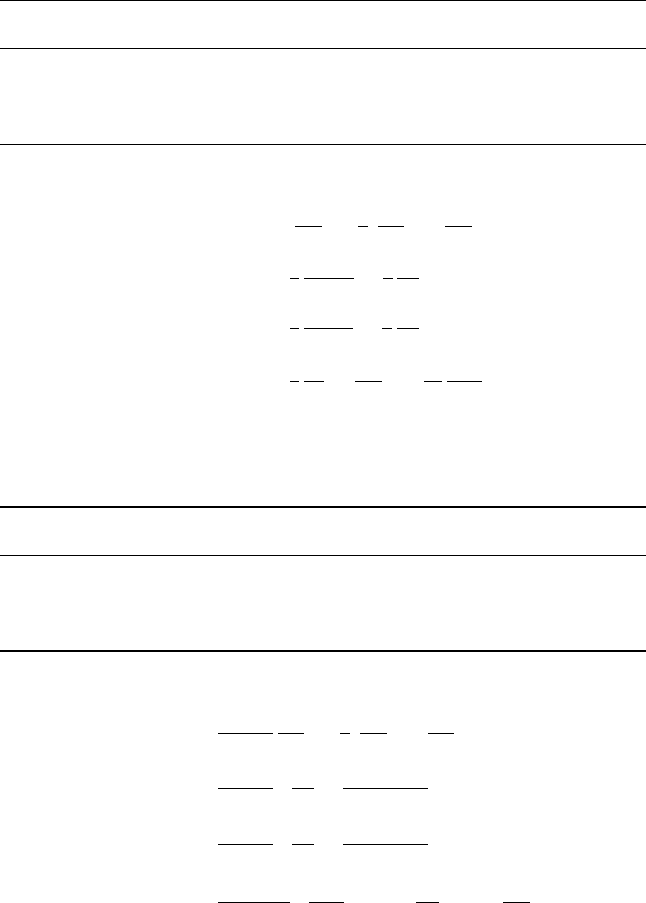
(b) Cylindrical coordinates: (r, λ, z)
Coordinate Symbol Velocity component Unit vector
Radial ru i
Azimuthal λv j
Upward zw k
∇ = i
∂
∂r
+ j
1
r
∂
∂λ
+ k
∂
∂z
∇·V =
1
r
∂
(
ru
)
∂r
+
1
r
∂v
∂λ
k ·
(
∇ × V
)
=
1
r
∂
(
rv
)
∂r
−
1
r
∂u
∂λ
∇
2
h
=
1
r
∂
∂r
r
∂
∂r
+
1
r
2
∂
2
∂λ
2
(c) Spherical coordinates: (λ, φ, r)
Coordinate Symbol Velocity component Unit vector
Longitude λu i
Latitude φv j
Height rw k
∇ =
i
r cos φ
∂
∂λ
+ j
1
r
∂
∂φ
+ k
∂
∂r
∇·V =
1
r cos φ
∂u
∂λ
+
∂
(
v cos φ
)
∂φ
k ·
(
∇ × V
)
=
1
r cos φ
∂v
∂λ
−
∂
(
u cos φ
)
∂φ
∇
2
h
=
1
r
2
cos
2
φ
∂
2
∂λ
2
+ cos φ
∂
∂φ
cos φ
∂
∂φ

January 27, 2004 17:12 Elsevier/AID aid
APPENDIX D
Moisture Variables
D.1 EQUIVALENT POTENTIAL TEMPERATURE
A mathematical expression for θ
e
can be derived by applying the first law of
thermodynamics to a mixture of 1 kg dry air plus q kg of water vapor (q, called
the mixing ratio, is usually expressed as grams of vapor per kilogram of dry air).
If the parcel is not saturated, the dry air satisfies the energy equation
c
p
dT −
d
(
p − e
)
p − e
RT = 0 (D.1)
and the water vapor satisfies
c
pv
dT −
de
e
R
∗
m
v
T = 0 (D.2)
where the motion is assumed to be adiabatic. Here, e is the partial pressure of
the water vapor, c
pv
the specific heat at constant pressure for the vapor, R
∗
the
universal gas constant, and m
v
the molecular weight of water. If the parcel is
saturated, then consdensation of −dq
s
kg vapor per kilogram dry air will heat the
501
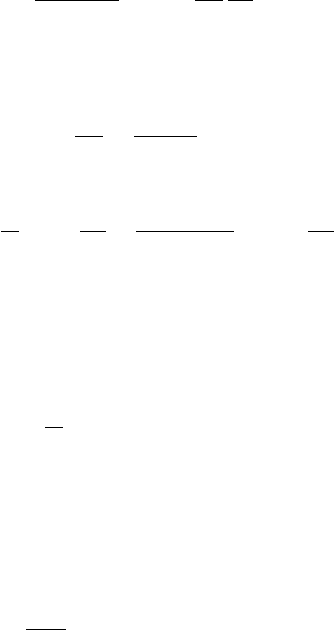
January 27, 2004 17:12 Elsevier/AID aid
502 D moisture variables
mixture of air and vapor by an amount of heat that goes into the liquid water, the
saturated parcel must satisfy the energy equation
c
p
dT +q
s
c
pv
dT −
d
(
p − e
s
)
p − e
s
RT − q
s
de
s
e
s
R
∗
m
v
T =−L
c
dq
s
(D.3)
where q
s
and e
s
are the saturation mixing ratio and vapor pressure, respectively.
The quantity de
s
/e
s
may be expressed in terms of temperature using the Clausius–
Clapeyron equation
1
de
s
dT
=
m
v
L
c
e
s
R
∗
T
2
(D.4)
Substituting from (D.4) into (D.3) and rearranging terms we obtain
−L
c
d
q
s
T
= c
p
dT
T
−
Rd
(
p − e
s
)
p − e
s
+ q
s
c
pv
dT
T
(D.5)
If we now define the potential temperature of the dry air θ
d
, according to
c
p
d ln θ
d
= c
p
d ln T − Rd ln
(
p − e
s
)
we can rewrite (D.5) as
−L
c
d
q
s
T
= c
p
d ln θ
d
+ q
s
c
pv
d ln T (D.6)
However, it may be shown that
dL
c
/dT = c
pv
− c
w
(D.7)
where c
w
is the specific heat of liquid water.Combining (D.7) and (D.6) to eliminate
c
pv
yields
−d
L
c
q
s
T
= c
p
d ln θ
d
+ q
s
c
w
d ln T (D.8)
Neglecting the last term in (D.8) we may integrate from the originial state (p, T ,
q
s
, e
s
, θ
d
) to a state where q
s
→ 0. Therefore, the equivalent potential temperature
of a saturated parcel is given by
θ
e
= θ
d
exp
L
c
q
s
/c
p
T
≈ θ exp
L
c
q
s
/c
p
T
(D.9)
Equation (D. 9) may also be applied to an unsaturated parcel provided that the tem-
perature used is the temperature that the parcel would have if brought to saturation
by an adiabatic expansion.
1
For a derivation, see Curry and Webster (1999, p. 108)
January 27, 2004 17:12 Elsevier/AID aid
D moisture variables 503
D.2 PSEUDOADIABATIC LAPSE RATE
Section 9.5.2 showed that from the first law of thermodynamics the lapse rate
for a saturated parcel undergoing pseudoadiabatic ascent can be obtained from the
formula
dT
dz
+
g
c
p
=−
L
c
c
p
∂q
s
∂T
p
dT
dz
−
∂q
s
∂p
T
ρg
(D.10)
Noting that q
s
∼
=
εe
s
/p, where ε = 0.622 is the ratio of the molecular weight of
water to that of dry air and utilizing (D.4), we can express the partial derivatives
in (D.10) as
∂q
s
∂p
T
≈−
q
s
p
and
∂q
s
∂T
p
≈
ε
p
∂e
s
∂T
=
ε
2
L
c
e
s
pRT
2
=
εL
c
q
s
RT
2
Substitution into (D.10), and noting that g/c
p
=
d
, then yields the desired result:
s
≡−
dT
dz
=
d
[
1 + L
c
q
s
/
(
RT
)
]
1 + εL
2
c
q
s
/
c
p
RT
2

January 27, 2004 17:12 Elsevier/AID aid
APPENDIX E
Standard Atmosphere Data
Table E.1 Geopotential Height versus Pressure
Pressure (hPa) Z (km)
1000 0.111
900 0.988
850 1.457
700 3.012
600 4.206
500 5.574
400 7.185
300 9.164
250 10.363
200 11.784
150 13.608
100 16.180
50 20.576
30 23.849
20 26.481
10 31.055
504

January 27, 2004 17:12 Elsevier/AID aid
E standard atmosphere data 505
Table E.2 Standard Atmosphere Temperature, Pressure, and Density as a Function of Geopo-
tential Height
Z (km) Temperature (K) Pressure (hPa) Density (kg m
−3
)
0 288.15 1013,25 1.225
1 281.65 898.74 1.112
2 275.15 794.95 1.007
3 268.65 701.08 0.909
4 262.15 616.40 0.819
5 255.65 540.19 0.736
6 249.15 471.81 0.660
7 242.65 410.60 0.590
8 236.15 355.99 0.525
9 229.65 307.42 0.466
10 223.15 264.36 0.412
12 216.65 193.30 0.311
14 216.65 141.01 0.227
16 216.65 102.87 0.165
18 216.65 75.05 0.121
20 216.65 54.75 0.088
24 220.65 29.30 0.046
28 224.65 15.86 0.025
32 228.65 08.68 0.013

January 27, 2004 17:12 Elsevier/AID aid
APPENDIX F
Symmetric Baroclinic
Oscillations
A variant of the derivation of the Sawyer–Eliassen equation for forced transverse
circulations in baroclinic zones (9.15) can be used to obtain an equation for free
symmetric transverse oscillations, which can be used to derivean expression for the
growthrate of unstable symmetric oscillations or the frequency of stable symmetric
oscillations.
Suppose that the flow field is zonally symmetric so that u
g
= u
g
(
y,z
)
and
b = b
(
y,z
)
. The ageostrophic (transverse) flow is given by the streamfunction
ψ
(
y,z
)
go that v
a
=−∂ψ
∂z; w
a
= ∂ψ
∂y. Then from (9.12) Q
2
= 0 so that
any transverse circulation is unforced and must arise from a departure from exact
geostrophic balance. This can be simply represented by adding an acceleration
term in the y-momentum equation so that (9.10) becomes
∂
∂t
−
∂
2
ψ
∂z
2
+ f
∂u
g
∂z
+
∂b
∂y
= 0 (F.1)
Then combining (9.11) and (9.13) as before and applying (F.1), we obtain
D
Dt
∂
∂t
∂
2
ψ
∂z
2
+ N
2
s
∂
2
ψ
∂y
2
+ F
2
∂
2
ψ
∂z
2
+ 2S
2
∂
2
ψ
∂y∂z
= 0(F.2)
506

January 27, 2004 17:12 Elsevier/AID aid
F symmetric baroclinic oscillations 507
Neglecting terms quadratic in the streamfunction
D
Dt
=
∂
∂t
+ v
a
∂
∂y
+ w
a
∂
∂z
≈
∂
∂t
then yields the desired result
∂
2
∂t
2
∂
2
ψ
∂z
2
+ N
2
s
∂
2
ψ
∂y
2
+ F
2
∂
2
ψ
∂z
2
+ 2S
2
∂
2
ψ
∂y∂z
= 0 (F.3)
