Hibbeler R.C. Structural Analysis
Подождите немного. Документ загружается.


460 CHAPTER 11 DISPLACEMENT METHOD OF A NALYSIS: SLOPE-DEFLECTION EQUATIONS
11
Draw the shear and moment diagrams for the beam shown in
Fig. 11–10a. EI is constant.
EXAMPLE 11.1
SOLUTION
Slope-Deflection Equations. Two spans must be considered in this
problem. Since there is no span having the far end pinned or roller
supported, Eq. 11–8 applies to the solution. Using the formulas for the
FEMs tabulated for the triangular loading given on the inside back
cover, we have
Note that is negative since it acts counterclockwise on the
beam at B. Also, since there is no load on
span AB.
In order to identify the unknowns, the elastic curve for the beam is
shown in Fig. 11–10b. As indicated, there are four unknown internal
moments. Only the slope at B, is unknown. Since A and C are fixed
supports, Also, since the supports do not settle, nor are
they displaced up or down, For span AB, considering
A to be the near end and B to be the far end, we have
(1)
Now, considering B to be the near end and A to be the far end, we have
(2)
In a similar manner, for span BC we have
(3)
(4) M
CB
= 2Ea
I
6
b[2102+ u
B
- 3102] + 10.8 =
EI
3
u
B
+ 10.8
M
BC
= 2Ea
I
6
b[2u
B
+ 0 - 3102] - 7.2 =
2EI
3
u
B
- 7.2
M
BA
= 2Ea
I
8
b[2u
B
+ 0 - 3102] + 0 =
EI
2
u
B
M
AB
= 2Ea
I
8
b[2102+ u
B
- 3102] + 0 =
EI
4
u
B
M
N
= 2Ea
I
L
b12u
N
+ u
F
- 3c2+ 1FEM2
N
c
AB
= c
BC
= 0.
u
A
= u
C
= 0.
u
B
,
1FEM2
AB
= 1FEM2
BA
= 0
1FEM2
BC
1FEM2
BC
=-
wL
2
30
=-
6162
2
30
=-7.2 kN
#
m
1FEM2
CB
=
wL
2
20
=
6162
2
20
= 10.8 kN
#
m
A
B
(a)
8 m 6 m
C
6 kN/m
A
B
C
M
BA
M
BC
u
B
u
B
M
CB
M
AB
(b)
Fig. 11–10

11.3 ANALYSIS OF BEAMS 461
11
Equilibrium Equations. The above four equations contain five
unknowns. The necessary fifth equation comes from the condition of
moment equilibrium at support B.The free-body diagram of a segment
of the beam at B is shown in Fig. 11–10c. Here and are
assumed to act in the positive direction to be consistent with the slope-
deflection equations.* The beam shears contribute negligible moment
about B since the segment is of differential length. Thus,
(5)
To solve, substitute Eqs. (2) and (3) into Eq. (5), which yields
Resubstituting this value into Eqs. (1)–(4) yields
The negative value for indicates that this moment acts counter-
clockwise on the beam, not clockwise as shown in Fig. 11–10b.
Using these results, the shears at the end spans are determined from
the equilibrium equations, Fig. 11–10d. The free-body diagram of
the entire beam and the shear and moment diagrams are shown in
Fig. 11–10e.
M
BC
M
CB
= 12.86 kN
#
m
M
BC
=-3.09 kN
#
m
M
BA
= 3.09 kN
#
m
M
AB
= 1.54 kN
#
m
u
B
=
6.17
EI
M
BA
+ M
BC
= 0d+©M
B
= 0;
M
BC
M
BA
M
BC
V
B
R
V
B
L
M
BA
(c)
B
y
8 m
1.54 kNm
A
y
0.579 kN
B
y
L
0.579 kN
3.09 kNm
(d)
6 m
6 kN/m
B
y
R
4.37 kN
3.09 kNm
C
y
13.63 kN
12.86 kNm
4.95 kN
0.579 kN
1.54 kNm
13.63 kN
12.86 kNm
0.579
V (kN)
81410.96
x (m)
4.37
13.63
1.54
M (kNm)
8
14
10.96
x (m)
3.09
12.86
2.67
(e)
6 kN/m
5.47
*Clockwise on the beam segment, but—by the principle of action, equal but opposite
reaction—counterclockwise on the support.

462 CHAPTER 11 DISPLACEMENT METHOD OF A NALYSIS: SLOPE-DEFLECTION EQUATIONS
11
SOLUTION
Slope-Deflection Equations. Two spans must be considered in this
problem. Equation 11–8 applies to span AB. We can use Eq. 11–10 for
span BC since the end C is on a roller. Using the formulas for the
FEMs tabulated on the inside back cover, we have
Note that and are negative since they act
counterclockwise on the beam at A and B, respectively. Also, since the
supports do not settle, Applying Eq. 11–8 for span
AB and realizing that we have
(1)
(2)
Applying Eq. 11–10 with B as the near end and C as the far end, we have
(3)
Remember that Eq. 11–10 is not applied from C (near end) to B
(far end).
M
BC
= 0.375EIu
B
- 18
M
BC
= 3Ea
I
8
b1u
B
- 02- 18
M
N
= 3Ea
I
L
b1u
N
- c2+ 1FEM2
N
M
BA
= 0.1667EIu
B
+ 96
M
BA
= 2Ea
I
24
b[2u
B
+ 0 - 3102] + 96
M
AB
= 0.08333EIu
B
- 96
M
AB
= 2Ea
I
24
b[2102+ u
B
- 3102] - 96
M
N
= 2Ea
I
L
b12u
N
+ u
F
- 3c2+ 1FEM2
N
u
A
= 0,
c
AB
= c
BC
= 0.
1FEM2
BC
1FEM2
AB
1FEM2
BC
=-
3PL
16
=-
31122182
16
=-18 k
#
ft
1FEM2
BA
=
wL
2
12
=
1
12
1221242
2
= 96 k
#
ft
1FEM2
AB
=-
wL
2
12
=-
1
12
1221242
2
=-96 k
#
ft
EXAMPLE 11.2
Draw the shear and moment diagrams for the beam shown in Fig. 11–11a.
EI is constant.
8 ft24 ft
4 ft
2 k/ft
B
A
C
12 k
(a)
Fig. 11–11

11.3 ANALYSIS OF BEAMS 463
11
Equilibrium Equations. The above three equations contain four
unknowns. The necessary fourth equation comes from the conditions
of equilibrium at the support B. The free-body diagram is shown in
Fig. 11–11b. We have
(4)
To solve, substitute Eqs. (2) and (3) into Eq. (4), which yields
Since is negative (counterclockwise) the elastic curve for the
beam has been correctly drawn in Fig. 11–11a. Substituting into
Eqs. (1)–(3), we get
Using these data for the moments, the shear reactions at the ends
of the beam spans have been determined in Fig. 11–11c. The shear
and moment diagrams are plotted in Fig. 11–11d.
M
BC
=-72.0 k
#
ft
M
BA
= 72.0 k
#
ft
M
AB
=-108.0 k
#
ft
u
B
u
B
u
B
=-
144.0
EI
M
BA
+ M
BC
= 0d+©M
B
= 0;
72 kft72 kft
V
B
R
15 kV
B
R
15 k
4 ft4 ft 4 ft4 ft
12 k12 k
72 kft72 kft
V
B
L
22.5 kV
B
L
22.5 k
C
y
3.0 kC
y
3.0 k
48 k48 k
V
A
25.5 kV
A
25.5 k
108 kft108 k ft
12 ft12 ft 12 ft12 ft
(c)(c)
V (k)
x (ft)
25.5
22.5
12.75
15
24 28
3
32
(
d
)
M (kft)
x (ft)
108
72
12.75
54.6
24 28
32
12
B
M
B
C
V
B
R
B
y
V
B
L
M
BA
(b)

464 CHAPTER 11 DISPLACEMENT METHOD OF A NALYSIS: SLOPE-DEFLECTION EQUATIONS
11
EXAMPLE 11.3
Determine the moment at A and B for the beam shown in Fig. 11–12a.
The support at B is displaced (settles) 80 mm. Take
I = 5110
6
2 mm
4
.
E = 200 GPa,
4 m
3 m
A
B
C
8 kN
(a)
B
c
BA
c
AB
A
(b)
Fig. 11–12
(1)
(2)M
BA
= 21200110
9
2 N>m
2
2[1.25110
-6
2 m
3
][2u
B
+ 0 – 310.022] + 0
- 310.022] + 0M
AB
= 21200110
9
2 N>m
2
2[1.25110
-6
2 m
3
][2102+ u
B
Equilibrium Equations. The free-body diagram of the beam at
support B is shown in Fig. 11–12c. Moment equilibrium requires
Substituting Eq. (2) into this equation yields
Thus, from Eqs. (1) and (2),
M
BA
= 24.0 kN
#
m
M
AB
=-3.00 kN
#
m
u
B
= 0.054 rad
1110
6
2u
B
- 30110
3
2= 24110
3
2
M
BA
- 8000 N13 m2= 0d+©M
B
= 0;
SOLUTION
Slope-Deflection Equations. Only one span (AB) must be considered
in this problem since the moment due to the overhang can be
calculated from statics. Since there is no loading on span AB, the
FEMs are zero. As shown in Fig. 11–12b, the downward displacement
(settlement) of B causes the cord for span AB to rotate clockwise.
Thus,
The stiffness for AB is
Applying the slope-deflection equation, Eq. 11–8, to span AB, with
we have
M
N
= 2Ea
I
L
b12u
N
+ u
F
- 3c2+ 1FEM2
N
u
A
= 0,
k =
I
L
=
5110
6
2 mm
4
110
-12
2 m
4
>mm
4
4 m
= 1.25110
-6
2 m
3
c
AB
= c
BA
=
0.08 m
4
= 0.02 rad
M
BC
8000 N8000 N
B
y
B
y
M
BA
M
BA
8000 N(3 m)8000 N(3 m)
V
B
L
V
B
L
(c)(c)

11.3 ANALYSIS OF BEAMS 465
11
EXAMPLE 11.4
Determine the internal moments at the supports of the beam shown
in Fig. 11–13a. The roller support at C is pushed downward 0.1 ft by
the force P. Take I = 1500 in
4
.E = 29110
3
2 ksi,
SOLUTION
Slope-Deflection Equations. Three spans must be considered in
this problem. Equation 11–8 applies since the end supports A and D
are fixed. Also, only span AB has FEMs.
As shown in Fig. 11–13b, the displacement (or settlement) of the
support C causes to be positive, since the cord for span BC rotates
clockwise, and to be negative, since the cord for span CD rotates
counterclockwise. Hence,
Also, expressing the units for the stiffness in feet, we have
Noting that since A and D are fixed supports, and
applying the slope-deflection Eq. 11–8 twice to each span, we have
u
A
= u
D
= 0
k
CD
=
1500
151122
4
= 0.004823 ft
3
k
AB
=
1500
241122
4
= 0.003014 ft
3
k
BC
=
1500
201122
4
= 0.003617 ft
3
c
BC
=
0.1 ft
20 ft
= 0.005 rad
c
CD
=-
0.1 ft
15 ft
=-0.00667 rad
c
CD
c
BC
1FEM2
BA
=
wL
2
12
=
1
12
11.521242
2
= 72.0 k
#
ft
1FEM2
AB
=-
wL
2
12
=-
1
12
11.521242
2
=-72.0 k
#
ft
24 ft
A
B
C
(a)
20 ft 15 ft
D
1.5 k/ft
P
C
B
0.1 ft
c
CD
c
CD
c
BC
c
BC
(b)
20 ft 15 ft
D
Fig. 11–13

EXAMPLE 11.4 (Continued)
466 CHAPTER 11 DISPLACEMENT METHOD OF A NALYSIS: SLOPE-DEFLECTION EQUATIONS
11
For span AB:
(1)
(2)
For span BC:
(3)
(4)
For span CD:
(5)
(6)
Equilibrium Equations. These six equations contain eight unknowns.
Writing the moment equilibrium equations for the supports at B and C,
Fig. 10–13c, we have
(7)
(8)
In order to solve, substitute Eqs. (2) and (3) into Eq. (7), and Eqs. (4)
and (5) into Eq. (8). This yields
Thus,
The negative value for indicates counterclockwise rotation of the tan-
gent at C, Fig. 11–13a. Substituting these values into Eqs. (1)–(6) yields
Ans.
Ans.
Ans.
Ans.
Ans.
Ans.
Apply these end moments to spans BC and CD and show that V
C
L
41.05 k, V
C
R
79.73 k and the force on the roller is P 121 k.
M
DC
= 667 k
#
ft
M
CD
= 529 k
#
ft
M
CB
=-529 k
#
ft
M
BC
=-292 k
#
ft
M
BA
= 292 k
#
ft
M
AB
= 38.2 k
#
ft
u
C
u
B
= 0.00438 rad u
C
=-0.00344 rad
-u
C
- 0.214u
B
= 0.00250
u
C
+ 3.667u
B
= 0.01262
M
CB
+ M
CD
= 0d+©M
C
= 0;
M
BA
+ M
BC
= 0d+©M
B
= 0;
M
DC
= 40 277.8u
C
+ 805.6
M
DC
= 2[29110
3
21122
2
]10.0048232[2102+ u
C
- 31-0.006672] + 0
M
CD
= 80 555.6u
C
+ 0 + 805.6
M
CD
= 2[29110
3
21122
2
]10.0048232[2u
C
+ 0 - 31-0.006672] + 0
M
CB
= 60 416.7u
C
+ 30 208.3u
B
- 453.1
M
CB
= 2[29110
3
21122
2
]10.0036172[2u
C
+ u
B
- 310.0052] + 0
M
BC
= 60 416.7u
B
+ 30 208.3u
C
- 453.1
M
BC
= 2[29110
3
21122
2
]10.0036172[2u
B
+ u
C
- 310.0052] + 0
M
BA
= 50 347.2u
B
+ 72
M
BA
= 2[29110
3
21122
2
]10.0030142[2u
B
+ 0 - 3102] + 72
M
AB
= 25 173.6u
B
- 72
M
AB
= 2[29110
3
21122
2
]10.0030142[2102+ u
B
- 3102] - 72
24 ft
A
B
C
(a)
20 ft 15 ft
D
1.5 k/ft
P
BB
M
BC
M
BC
V
B
R
V
B
R
B
y
B
y
V
B
L
V
B
L
M
BA
M
BA
(c)(c)
CC
PP
M
CD
M
CD
V
C
R
V
C
R
V
C
L
V
C
L
M
CB
M
CB
11.3 ANALYSIS OF BEAMS 467
11
3 m
6 m
A
25 kN/m
2 m 2 m
2 m
2 m
15 kN
15 kN
15 kN
B
C
25 kN
15 kN
/
m
3 m 3 m
4 m
ABC
A
24 ft
8 ft 8 ft
B
C
2 k/ft
30 k
I
AB
900 in.
4
I
BC
1200 in.
4
A
B
5 m
CD
3 m 5 m
20 kN/m
A
B C
D
5 ft
5 ft 5 ft15 ft15 ft
9 k
2 k/ft
9 k
A
B
C
3 ft 3 ft 3 ft
10 ft 10 ft
3 k 3 k 4 k
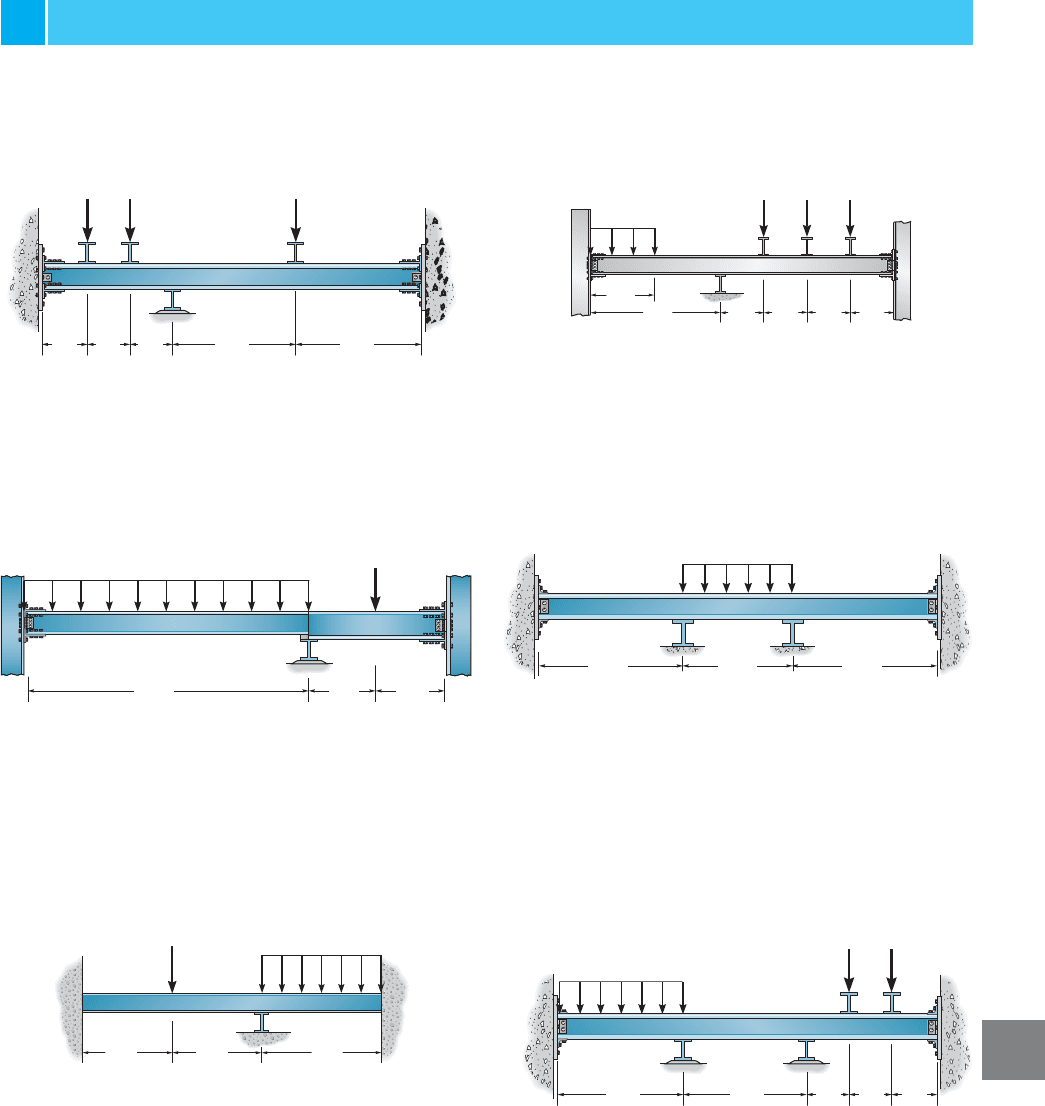
11–2. Determine the moments at A, B, and C, then draw
the moment diagram for the beam. The moment of inertia
of each span is indicated in the figure. Assume the support
at B is a roller and A and C are fixed. ksi.E = 29(10
3
)
11–5. Determine the moment at A, B, C and D, then draw
the moment diagram for the beam. Assume the supports at
A and D are fixed and B and C are rollers. EI is constant.
11–3. Determine the moments at the supports A and C,
then draw the moment diagram. Assume joint B is a roller.
EI is constant.
11–6. Determine the moments at A, B, C and D, then
draw the moment diagram for the beam. Assume the
supports at A and D are fixed and B and C are rollers. EI is
constant.
11–1. Determine the moments at A, B, and C and then
draw the moment diagram. EI is constant. Assume the
support at B is a roller and A and C are fixed.
*11–4.
Determine the moments at the supports, then
draw the moment diagram. Assume B is a roller and A
and C are fixed. EI is constant.
PROBLEMS
Prob. 11–2
Prob. 11–3
Prob. 11–4
Prob. 11–5
Prob. 11–1
Prob. 11–6

468 CHAPTER 11 DISPLACEMENT METHOD OF A NALYSIS: SLOPE-DEFLECTION EQUATIONS
11
11–7. Determine the moment at B, then draw the moment
diagram for the beam. Assume the supports at A and C are
pins and B is a roller. EI is constant.
11–10. Determine the moments at A and B, then draw the
moment diagram for the beam. EI is constant.
*11–8.
Determine the moments at A, B, and C, then
draw the moment diagram. EI is constant. Assume the
support at B is a roller and A and C are fixed.
*11–12. Determine the moments acting at A and B.
Assume A is fixed supported, B is a roller, and C is a pin. EI
is constant.
11–11. Determine the moments at A, B, and C, then draw
the moment diagram for the beam. Assume the support at
A is fixed, B and C are rollers, and D is a pin. EI is constant.
11–9. Determine the moments at each support, then draw
the moment diagram. Assume A is fixed. EI is constant.
A
BC
4 m
2 m
4 m
6 m
20 kN
40 kN
B
A
C
3 m
9 m
3 m
80 kN
20 kN/m
A
BCD
4 ft
4 ft 4 ft 12 ft 12 ft
6 k 6 k
3 k/ft
200 lb/ft
2400 lb
30 ft 10 ft
A BC
A
4 k/ft
20 ft 15 ft 8 ft 8 ft
B
C
D
12 k
8 ft 8 ft 18 ft
A
B
C
6 k
0.5 k/ft
Prob. 11–7
Prob. 11–8
Prob. 11–9
Prob. 11–10
Prob. 11–11
Prob. 11–12

11.4 ANALYSIS OF FRAMES: NO SIDESWAY 469
11
11.4 Analysis of Frames: No Sidesway
A frame will not sidesway, or be displaced to the left or right, provided
it is properly restrained. Examples are shown in Fig. 11–14. Also, no
sidesway will occur in an unrestrained frame provided it is symmetric
with respect to both loading and geometry, as shown in Fig. 11–15. For
both cases the term in the slope-deflection equations is equal to zero,
since bending does not cause the joints to have a linear displacement.
The following examples illustrate application of the slope-deflection
equations using the procedure for analysis outlined in Sec. 11–3 for these
types of frames.
c
w
P
ww ww ww
Fig. 11–14
Fig. 11–15
