Heubach S., Mansour T. Combinatorics of Compositions and Words

Подождите немного. Документ загружается.

74 Combinatorics of Compositions and Words

The corresponding Maple code for the series expansion is given by

taylor(1/(1- sum(x^ithprime(n), ’n’=1..20)), x=0, 20);

Mathematica also provides a command to get just the list of coeﬃcients, rather

than the series:

CoefficientList[Series[1/(1-Sum[x^Prime[n],{n,1,11}]),{x,0,30}],x]

We can read oﬀ the values for n =0, 1,...,30 as 1, 0, 1, 1, 1, 3, 2, 6, 6, 10,

16, 20, 35, 46, 72, 105, 152, 232, 332, 501, 732, 1081, 1604, 2352, 3493, 5136,

7595, 11212, 16534, 24442,and36039, which occur as sequence A023360 in

[180].

3.4 Connection betw een compositions and tilings

We have already seen two graphical representations of a composition,

namely the line graph introduced by MacMahon (see Chapter 1) and the bar

graph of a composition. Having diﬀerent ways to think about a composition

allows one to pick the viewpoint that is most useful for a given question. For

example, the line graph representation results in an easy combinatorial proof

for the total number of compositions and provides a quick way to obtain the

conjugate composition, whereas a description of the algorithm without the

line graph representation is very cumbersome. Last but not least, certain

questions arising naturally in one representation may be reframed into an-

other representation, with the potential of giving new insights or raising new

questions.

We will now look at the representation of a composition as a tiling of a

1 × n board with tiles of size 1 × k. The tiles correspond to the parts of the

composition in the obvious way. The tiling can also be connected to the line

graph as follows: A node in the line graph corresponds to the end of a tile, and

the lengths of the tiles correspond to the number of segments between nodes.

Figure 3.3 shows the tiling and line graph corresponding to the composition

2231. (Arranging the tiles in columns results in the bar graph.)

FIGURE 3.3: Correspondence between line graph and tiling.

Compositions 75

The simplest tiling problem is to enumerate the number of ways one can tile

a1×n board with 1×1 tiles, called squares,and1×2 tiles, called dominoes.

This tiling problem is identical to the question on the total number of com-

positions in {1, 2} studied by Alladi and Hoggatt [7]. We give the derivation

in terms of tilings.

Example 3.18 (Tiling with squares and dominoes) Suppose you are given a

large number of squares and dominoes. In how many diﬀerent ways can a

1×n board be tiled using these two types of tiles? Let T

denote the number

of tilings of a 1×n board, with T

=1. There is exactly one way to tile the

1×1 board. In general, for n ≥ 2, each tiling of a 1×n board either starts with

a square followed by a tiling of a 1×(n − 1) board (of which there T

n−1

) or a

domino, followed by a tiling of a 1×(n −2) board (of which there T

n−2

).Thus

we obtain the following recurrence relation:

= T

n−1

+ T

n−2

= T

=1.

This recursive relation is identical to that of the Fibonacci numbers, except

that the initial conditions are shifted. The resulting sequence is often denoted

by f

,withf

=1. Using Rule 2.45, the generating function for this shifted

sequence is given by

F (x) − F

1 − x − x

Tiling questions have been studied independently of compositions. Ques-

tions on square and domino tilings of larger boards arise for example from

questions in physics. There they are known as the monomer-dimer or dimer

problems, where monomers correspond to squares and dimers correspond to

dominoes (see for example [44, 66, 107, 106, 151, 167] and references therein).

3.5 Colored compositions and other variations

When looking at compositions in their representation as tilings of a 1×n

board, it is natural to ask about the total number of tilings when tiles of a

certain size come in several colors. Let A = {a

,...,a

} be the set of

possible sizes for the tiles, and let c

indicate the number of possible colors

for the tile of size a

. Then we can easily establish the following result.

Theorem 3.19 The number of tilings of a 1×n boardwithtilesofsizea

that

come in c

colors is given by



i=1

n−a

for n ≥ a

76 Combinatorics of Compositions and Words

with initial conditions T

=1, T

,...,T

This general recursion may be solved for speciﬁc values of A and the number

of colors c

Example 3.20 Let A = {1, 2, 3},andc

=1, c

=4,andc

=2.The

recurrence relation becomes

= T

n−1

+4T

n−2

+2T

n−3

which expresses the sequence {T

} as a convolution with the sequence {1, 4, 2}.

Thus we have

T (x)=1+c(x)T (x) ⇒ T (x)=

1 − c(x)

, (3.5)

where c(x) is the generating function for the (ﬁnite) sequence of colors. By

the deﬁnition of the generating function,

c(x)=x +4x

+2x

and therefore, T (x)=1/(1 − x − 4x

− 2x

). (This example arose in the

context of tilings of larger boards with L-shaped tiles and squares investigated

by Chinn et al. [49], which can be mapped to this particular tiling question on

the 1×n board.)

Another example of colored compositions was introduced by Agarwal [3],

which leads to a nice connection with Fibonacci numbers.

Deﬁnition 3.21 An n-color composition is a composition with parts in N in

which the part of size i exists in i diﬀerent colors.

Example 3.22 Distinguishing diﬀerent colors by a subscript for i ≥ 2,we

can write down the eight 3-color compositions of 3,namely

112

111.

We use (3.5) with c(x)=



∞

i=1

= x/(1 − x)

to obtain the generating

function for the n-colored compositions as

T (x)=

1 −

(1 − x)

1 − 3x + x

Note that this generating function diﬀers from the generating function given

in [3], as Agarwal uses T

=0instead of the convention we have followed,

deﬁning T

=1.

Compositions 77

Theorem 3.23 [3, Theorem 1] Let

C(n)(

C(m; n)) be the number of n-color

compositions of n (with m parts),andlet

C(x)(

C(m; x)) be the respective

generating functions, where

C(0) =

C(m;0) = 0 for all m.Then

C(m; x)=

(1 − x)

and

C(x)=

1 − 3x + x

The corresponding sequences are given by

C(m; n)=



n + m − 1

2m − 1



and

C(n)=F

where F

is the 2n-th Fibonacci number.

Agarwal [3] also presents a more general result in which the parts and

the colors for a given part can be restricted. He obtains recursions for the

generating functions and the number of n-color compositions of n that have

exactly m parts from the set [k] and which use only the ﬁrst r colors for each

of the parts.

Example 3.24 There are 21 n-color compositions of 6 with exactly two parts

from {1, 2, 3, 4},usingupto3 colors for each of the parts: six of the form

, six of the form 2

, and nine of the form 3

We now look at a variation of compositions, based on the representation

of the compositions as a bar graph. Cracked compositions are compositions

that have parts of size k with potential “cracks” between the cells in the bar

graph representation. In particular, cracks do not occur at the beginning or

at the end of the column. These cracks do not increase the size of the part,

but the diﬀerent possible crack patterns can be thought of as each giving rise

to a diﬀerent color. We indicate the occurrence of a crack by placing an “×”

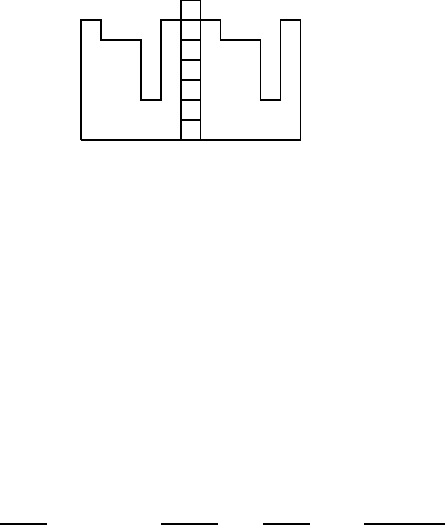
on the border between two successive cells. Figure 3.4 shows the bar graphs

of the cracked compositions for n =3.

× ×

FIGURE 3.4: Bar graphs of cracked compositions for n =3.

We will now answer a few questions about cracked compositions:

• How many compositions have exactly one crack?

78 Combinatorics of Compositions and Words

• How many compositions have at most one crack in each part?

• How many compositions have at most m cracks in each part?

To answer the ﬁrst question, we condition on where the part with the crack

occurs. If the cracked part occurs as the i-th part, then the preceding com-

position is just a regular composition (that is, with no cracks, and potentially

empty), and the remainder of the composition is also of that form.

FIGURE 3.5: Cracked compositions with exactly one crack.

We already know the generating function for compositions, so we just need

to compute the generating function for the cracked part. If there is exactly

one crack in the column, then there can be any number k

≥ 1 of cells below

the crack, and likewise any number k

≥ 1 above the crack. The generating

function counting the number of cells above or below the crack is given by

x/(1−x), and the number of these cells have to add to the height of the column.

By Rule 2.51, the generating function for the number of parts with exactly

one crack is the convolution of x/(1 − x) with itself. Thus, the generating

function A(x) for the number of cracked compositions with exactly one crack

is given by

A(x)=C(x)



1 − x



C(x)=



1 − x

1 − 2x





1 − x



(1 − 2x)

Note that this generating function is a convolution of

C(x) with itself, where

C(x)=x/(1 − 2x)=C(x) − 1 is the generating function for the nonempty

compositions.

Such an equality of two diﬀerent generating functions indicates that there

exists a bijection between the items counted by the two generating functions.

In this case, we are looking for a bijection between the cracked compositions

of n with exactly one crack and sequences that are created by concatenating

two nonempty compositions of sizes k and n − k,fork =1,...,n− 1. Note

that a given concatenated sequence may be obtained in several diﬀerent ways.

For example, the concatenated sequence 111 is obtained as 11|1or1|11, where

we place a | between the two compositions to clearly mark the concatenation

point.

Compositions 79

We now describe the bijection. To create a cracked composition with exactly

one crack, proceed as follows. Let σ

···σ

denote the ﬁrst composition, and

¯σ

···¯σ



the second one. For each value σ

, create a column of height σ

.Place

a crack on top of the last column of height σ

, then add ¯σ

cells above the

crack. This produces the piece with exactly one crack. Then create columns

of heights ¯σ

,...,¯σ



. Clearly, this process is reversible. Also, because both

compositions contain at least one part, we always create a cracked part, and

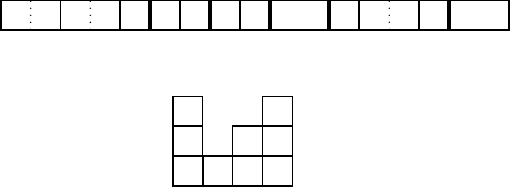
have therefore established the desired bijection. Figure 3.6 shows the cracked

compositions of 3 with exactly one crack and the corresponding concatenation

of two nonempty compositions.

1|2

1|11

11|1

2|1

FIGURE 3.6: Cracked compositions and associated sequences.

To answer the second question, we again break up the composition accord-

ing to the parts that have a crack. We can visualize the cracked composition

with at most one crack in each part as a sequence of ordinary compositions

interspersed with a part that has exactly one crack. Thus, if the composi-

tion has exactly m parts with one crack, then the generating function has the

structure

C(x)





1 − x



C(x)



Accounting for all possibilities, the generating function for the number of

cracked compositions that have at most one crack in each part is given by

A(x)=C(x)

∞



m=0





1 − x



C(x)



C(x)

1 −



1 − x



C(x)

1 − x

1 − 2x

1 −



1 − x



1 − x

1 − 2x

(1 − x)

1 − 3x + x

=1+

1 − 3x + x

Again, we obtain a generating function of a known sequence, in this case the

sequence {a

}

∞

n=1

,wherea

=1anda

= F

for n ≥ 1, where F

is the

n-th Fibonacci number (see Exercise 2.12). Since F

counts the number of

80 Combinatorics of Compositions and Words

tilings of a 1×(2n − 1) board with squares and dominoes, we are looking for

a bijection between the cracked compositions of n with at most one crack per

part and the tilings of the 1×(2n − 1) board.

We will now describe the bijection, starting with a tiling of a 1 × (2n − 1)

board with squares and dominoes. Given such a tiling, make cuts at odd

positions, unless there is a domino that spans across the odd position. Note

that the leftmost piece resulting from those cuts covers an odd number of

cells, whereas all the other pieces have an even number of cells. In addition,

• the ﬁrst piece is either a single square or consists of k ≥ 1dominoes

followed by a single square; and

• the remaining pieces consist either of a pair of squares, a single domino,

or a square followed by a sequence of k ≥ 1 dominoes ending in a square.

For a given tiling, the bar graph is created as follows:

• If the tiling starts with a square, then create a column of height 1; if it

starts with k dominoes followed by a square, create a column of height

k +1with acrackatlevelk.

• A pair of squares starts a new column of height 1.

• A single domino adds a cell on top of the rightmost column created so

far.

• A sequence of k ≥ 1 dominoes enclosed by a square on either side creates

a new column of height k +1 withacrackatheightk.

This process is reversible, and therefore we have found the desired bijection.

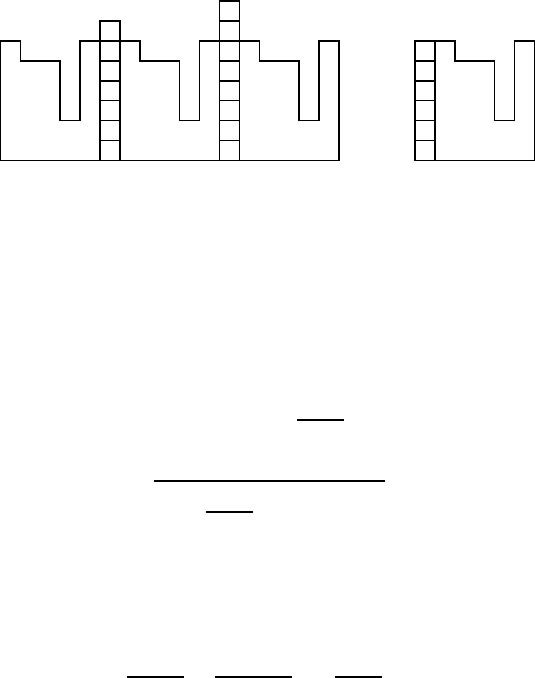
We illustrate the process in Example 3.25 using Figure 3.7.

13 57 911131517



FIGURE 3.7: Tiling and associated cracked composition.

Compositions 81

Example 3.25 The ﬁrst segment of the tiling consists of two dominoes fol-

lowed by a square, which creates a bar of height three with a crack at height

two. The next segment, consisting of two squares, starts a new column of

height one, as does the next segment. The domino of the fourth segment adds

a cell in the third bar. The ﬁfth segment, consisting of one domino enclosed

by squares starts a new bar of height two, with a crack at height one. Finally,

the domino at the end of the tiling adds a cell on the rightmost bar.

The third question about cracked compositions is a generalization of the

second one, so let’s see what we need to adjust when we set up the generating

function. Let C

(x) be the generating function for cracked compositions that

have parts with at most m cracks. Again we split up the composition, now

according to the parts that have exactly m cracks, as indicated in Figure 3.8

for m =2.

···

FIGURE 3.8: Cracked compositions with at most two cracks per part.

Then the compositions preceding the ﬁrst such part, and the compositions

between the parts with m cracks each have at most m −1cracks,andsotheir

generating function is given by C

m−1

(x). The generating function for the part

with exactly m cracks is given by (x/(1 −x))

m+1

(why?), and we get that

(x)=C

m−1

(x)

∞



i=0





1 − x



m+1

m−1

(x)



m−1

(x)

1 −



1 − x



m+1

m−1

(x)

Dividing the numerator and denominator of the right-hand side by C

m−1

(x)

and then cross-multiplying results in a recurrence relation for 1/C

(x)instead

of the one for C

(x):

(x)

m−1

(x)

−



1 − x



m+1

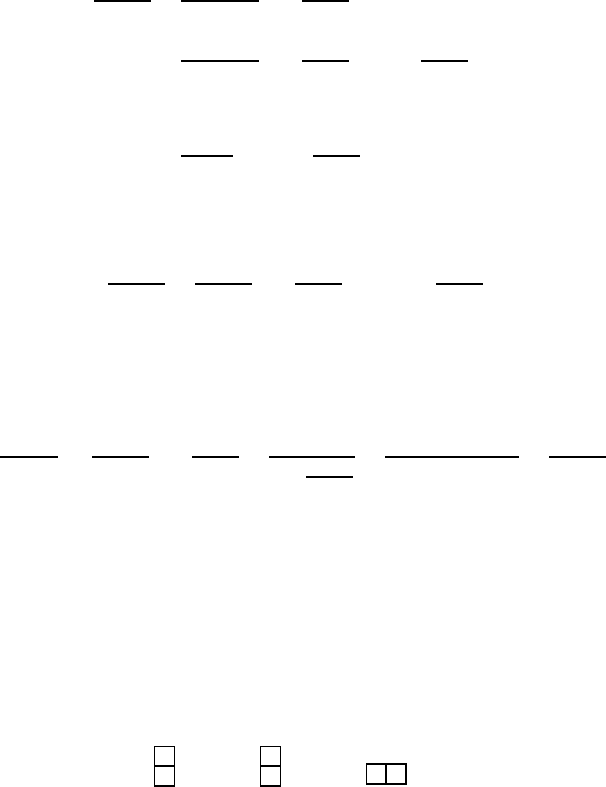
82 Combinatorics of Compositions and Words

This is a useful trick to have in one’s toolbox for solving recurrence relations,

and we will see it again in a later section. Now we use iteration to obtain that

for m ≥ 1,

(x)

m−1

(x)

−



1 − x



m+1

m−2

(x)

−



1 − x



−



1 − x



m+1

= ···

(x)

−

m+1



i=2



1 − x



which implies that

(x)

1 − 2x

1 − x

−



1 − x



m−1



i=0



1 − x



(3.6)

since C

(x)=C(x). The desired generating function for the number of

cracked compositions with at most m cracks is given by the reciprocal. If

we now let m →∞, we obtain that

(x)

→

1 − 2x

1 − x

−



1 − x



1 −

1 − x

(1 − 2x)

− x

(1 − 2x)(1 − x)

1 − 3x

1 − 2x

Thus, the generating function for the number of cracked compositions that

allow any number of cracks is given by (1 − 2x)/(1 − 3x). This is, however,

the generating function for words of length n −1 on the alphabet {1, 2, 3} (see

Exercise 2.4), so another bijection is lurking in the background waiting to be

discovered – here it is! We start with a word of length n −1 and describe the

associated cracked composition of n.

For n = 2, we associate the three types of cracked compositions with the

letters 1, 2, and 3 as follows:

↔ 1,

↔ 2,

↔ 3.

To create the words of length n we append either a 1, 2 or 3 to each of the

words of length n − 1. Here is how the associated cracked compositions of

n + 1 are created from the cracked compositions of n:

• If a 1 is appended to the word, then we add a cell on top of the rightmost

column of the bar graph corresponding to the word of length n − 1.

Compositions 83

• If a 2 is appended to the word, then we add a crack and a cell on the

top of the rightmost column of the bar graph corresponding to the word

of length n − 1.

• If a 3 is appended to the word, then we add a new column of height one

to the right end of the bar graph corresponding to the word of length

n − 1.

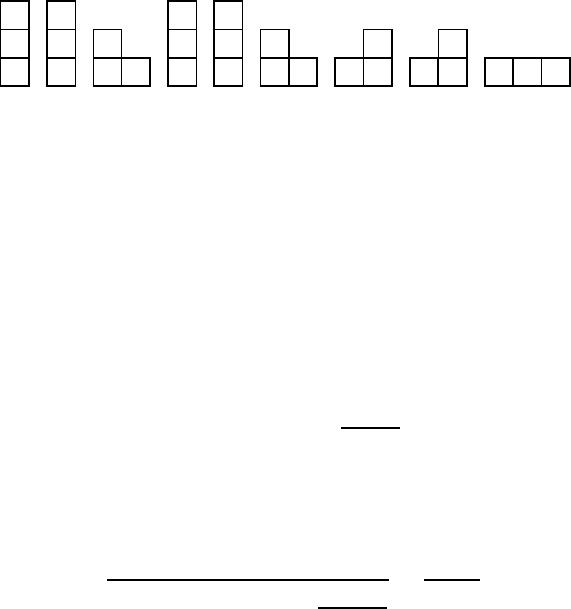
Figure 3.9 shows the correspondence of cracked compositions of n =3and

words of length two. The process described above is reversible (the last column

of a bar graph is either of height 1, or has a cell with a crack or a cell without

a crack at the top of a column of height at least 2). Therefore, we have found

a bijection between the cracked compositions of n with any number of cracks

and the words of length n −1 on the alphabet {1, 2, 3}.

12 13

23 31

32 33

FIGURE 3.9: Bijection between cracked compositions and words.

We summarize the results on cracked compositions in the following theorem.

Theorem 3.26 Let C(x) be the generating function for the number of com-

positions of n,

C(x) be the generating function for the number of nonempty

compositions of n,andC

(x) be the generating function for the cracked com-

positions of n with at most m cracks per part. Then

(1) The generating function for the number of cracked compositions with

exactly one crack is given by

(x)=

(1−2x)

(2) C

(x)=1+x/(1 −3x + x

), and therefore, [x

(x)=F

for n ≥ 1.

(3) More generally,

(x)=

(1 − x)

1 − 3x + x

− x



m−1

i=1

(1 − x)

→

1 − 2x

1 − 3x

as m →∞.

Thus, the number of cracked compositions of n with any number of

cracks is given by 3

n−1

for n ≥ 1.